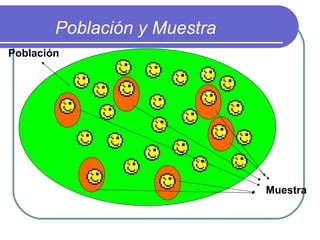
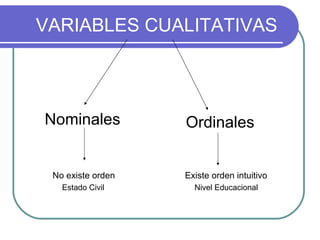
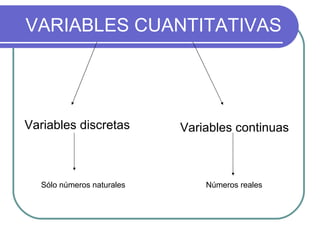
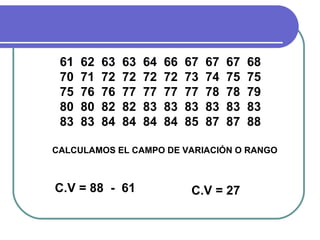
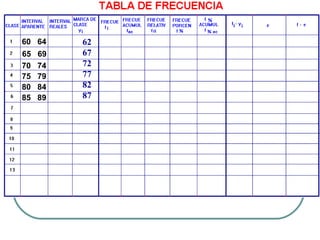
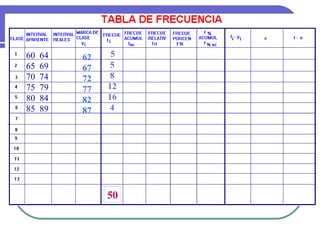
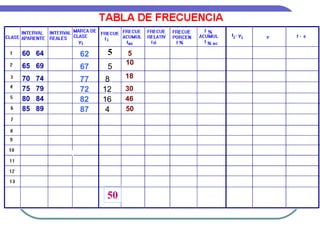
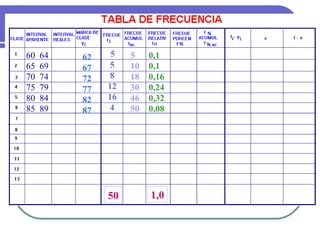
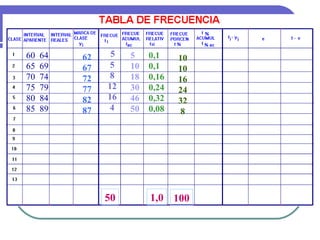
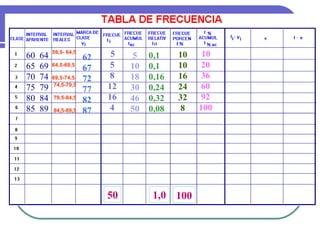
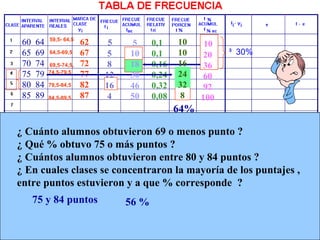
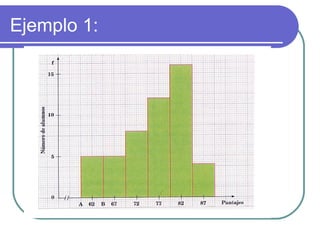
Este documento describe los conceptos básicos de la estadística. Explica que la estadística es la ciencia que analiza datos para extraer conclusiones válidas. Se divide en estadística descriptiva, que describe datos numéricamente, y estadística inferencial, que usa muestreo para inferir conclusiones sobre una población. También define conceptos como población, muestra, variables y métodos básicos como tablas de frecuencia y gráficos.

2. LA ESTADÍSTICA ES LA CIENCIA QUE
PROVEE DE MÉTODOS QUE PERMITEN
RECOGER, ORGANIZAR ,RESUMIR,
PRESENTAR Y ANALIZAR DATOS
RELATIVOS A UN CONJUNTO DE
INDIVIDUOS U OBSERVACIONES , PARA
ASÍ , EXTRAER CONCLUSIONES VÁLIDAS
Y TOMAR DECISIONES LÓGICAS
BASADAS EN DICHOS ANÁLISIS.

3. LA ESTADÍSTICA SE DIVIDE EN DOS
TIPOS:
A) ESTADÍSTICA DESCRIPTIVA
B) ESTADÍSTICA INFERENCIAL O
DEDUCTIVA

4. LA ESTADÍSTICA DESCRIPTIVA :
SE REFIERE A LA DESCRIPCIÓN
NUMÉRICA DE UN GRUPO PARTICULAR.
NINGUNA CONCLUSIÓN PUEDE IR MÁS
ALLÁ DEL GRUPO DESCRITO.
LOS DATOS ANALIZADOS , DESCRIBEN
ESTE GRUPO Y SÓLO ÉSTE .

5. ESTADÍSTICA INFERENCIAL
ES EL EMPLEO DE LA TÉCNICA DE
MUESTREO PARA LLEGAR A
DETERMINADAS CONCLUSIONES
ACERCA DE LA POBLACIÓN
DE LA CUAL SE HAN OBTENIDO LAS
MUESTRAS

7. POBLACIÓN
SE LLAMA POBLACIÓN AL CONJUNTO
FORMADO POR TODOS LOS
ELEMENTOS CUYO CONOCIMIENTO
NOS INTERESA . CADA UNO
DE ESTOS ELEMENTOS LO
DENOMINAREMOS INDIVIDUO .

8. MUESTRA
SE LLAMA MUESTRA A UN
SUBCONJUNTO FINITO DE LA
POBLACIÓN
EN ESTUDIO . SE USA UNA MUESTRA
CUANDO ES IMPOSIBLE
( O POCO PRÁCTICO) ESTUDIAR A
TODOS LOS INDIVIDUOS DE UNA
POBLACIÓN .

9. Población y Muestra
Población
Muestra

10. Concepto de Variable
Una variable en estadística
corresponde a la o las características
que se miden en la muestra. Las
variables pueden ser:
a) CUANTITATIVAS (Se pueden medir
numéricamente)
b) CUALITATIVAS (No se pueden
medir numéricamente)

11. VARIABLES CUALITATIVAS
Nominales Ordinales
No existe orden Existe orden intuitivo
Estado Civil Nivel Educacional

12. VARIABLES CUANTITATIVAS
Variables discretas Variables continuas
Sólo números naturales Números reales

13. BUEN MÉTODO ESTADÍSTICO
a) SELECCIÓN Y RECOPILACIÓN DE
LOS DATOS A ESTUDIAR EN UNA
MUESTRA O POBLACIÓN .
b) CLASIFICACIÓN Y ORDENACIÓN DE
LOS DATOS .
c) TABULACIÓN DE LOS DATOS

14. d) CÁLCULO DE ALGUNOS
PARÁMETROS ESTADÍSTICOS QUE
COMPLETEN LA INFORMACIÓN .
e) ENTREGA O PUBLICACIÓN DE LA
INFOMACIÓN . PARA ELLO ES USUAL
UTILIZAR LOS DISTINTOS GRÁFICOS
ESTADÍSTICOS .

15. CONSTRUCCIÓN DE UNA TABLA DE
DISTRIBUCIÓN DE FRECUENCIA
REGLAS GENERALES
1 ) LOS DATOS SE ORDENAN DE
MENOR A MAYOR
2 ) SE DETERMINA EL CAMPO DE
VARIACIÓN (RECORRIDO DE LA
VARIABLE) .
C.v. = X(max.) - X(min.)
SE SELECCIONA LA AMPLITUD DE LOS INTERVALOS

16. EJEMPLO
EN UN GRUPO DE 50 ALUMNOS EN UNA PRUEBA SE
REGISTRARON LOS SIGUIENTES PUNTAJES .
61 70 77 82 63 75 83 62 67
83
67 80 77 85 83 76 83 67 78
76
72 80 83 72 84 71 77 82 79
83
EN PRIMER LUGAR SE ORDENAN LOS DATOS DE MENOR A
MAYOR 88 68 74 84 75 73 75 83
66
84
87 64 83 72 87 77 63 72 84

17. 61 62 63 63 64 66 67 67 67 68
70 71 72 72 72 72 73 74 75 75
75 76 76 77 77 77 77 78 78 79
80 80 82 82 83 83 83 83 83 83
83 83 84 84 84 84 85 87 87 88
2 ) CALCULAMOS EL CAMPO DE VARIACIÓN O RANGO
C.V = 88 - 61 C.V = 27

18. 3 ) SE SELECCIONA LA AMPLITUD
DE
LOS INTERVALOS.
a ) CUANDO SE TIENE UN CONJUNTO
DE DATOS Y SE ESPECIFICA EL
NÚMERO DE INTERVALOS PARA LA
TABLA, LA AMPLITUD “a”, SE TIENE :
Campo de variación
a=
N° de intervalos

19. EN CASO DE OBTENER UN NÚMERO DECIMAL PARA “a” , SE
APROXIMA AL ENTERO MAS CERCANO.
4 ) SE DETERMINAN LOS INTERVALOS
I ) EL NÚMERO DE INTERVALO RECIBE EL NOMBRE DE CLASE .
II ) LOS INTERVALOS QUEDAN CARACTERIZADOS POR LAS
MARCAS DE CLASES QUE SON LOS PUNTOS MEDIOS O
SEMISUMA DE LOS LÍMITES SUPERIORES E INFERIORES, ÉSTE
NORMALMENTE ES POSITIVA .

20. CALCULAMOS LA AMPLITUD
“a”
TENIENDO EN CUENTA QUE LA CANTIDAD DE
DATOS ES PEQUEÑA , LOS AGRUPAREMOS EN
SOLO 6 CLASES
LUEGO TENEMOS :
Cv 27
a= a= a = 4,5
6 6
SIEMPRE SE APROXIMA LA AMPLITUD AL ENTERO
MAS CERCANO
LUEGO : a =5

21. 60 64 62
65 69 67
70 74 72
75 79 77
80 84 82
85 89 87

22. 5 ) SE REALIZA LA TABULACIÓN
FRECUENCIA o
FRECUENCIA ABSOLUTA:
ES EL NÚMERO DE VECES QUE SE
REPITE EL VALOR DE UN DATO , O EL
NÚMERO DE INDIVIDUOS QUE
PERTENECEN A LA MISMA CLASE. SE
SIMBOLIZA POR
fi

23. 60 64 62 5
65 69 67 5
70 74 72 8
75 79 77 12
80 84 82 16
85 89 87 4
50

24. FRECUENCIA ACUMULADA
PARA CADA VALOR ES LA SUMA DE
SU FRECUENCIA MAS LAS
ANTERIORES,
SE SIMBOLIZA POR fac

25. 60 64 62 5 5
65 69 67
55
10
70 74
8 18
77 8
75 79 72 12
12 30
80 84 82 16
16 46
85 89 87 4 50
4
50

26. FRECUENCIA RELATIVA
ES EL NÚMERO DE VECES QUE SE
REPITE UN DATO O CLASE, REFERIDO
AL TOTAL DE INDIVIDUOS. ESTA
FRECUENCIA RELATIVA SE
SIMBOLIZA POR fri , Y SE
CALCULA :
fi
fri = ; n , es el número total de elementos
n

27. 60 64 62 5 5 0,1
65 69 67 5 10 0,1
70 74 72 8 18 0,16
75 79 77 12 30 0,24
80 84 82 16 46 0,32
85 89 87 4 50 0,08
50 1,0

28. FRECUENCIA PORCENTUAL
ES EXPRESAR LA FRECUENCIA EN
FORMA DE PORCENTAJE , PARA TAL
EFECTO SE TOMA LA FRECUENCIA
RELATIVA Y SE CORRE LA COMA DOS
ESPACIOS O SE MULTIPLICA POR 100
SE SIMBOLIZA POR : f%

29. 60 64 62 5 5 0,1 10
65 69 67 5 10 0,1 10
70 74 72 8 18 0,16 16
75 79 77 12 30 0,24 24
80 84 82 16 46 0,32 32
85 89 87 4 50 0,08 8
50 1,0 100

30. FRECUENCIA PORCENTUAL
ACUMULADA
ES EXPRESAR EN FORMA ACUMULADA
LA FRECUENCIA PORCENTUAL

31. 60 64 59,5- 64,5
62 5 5 0,1 10 10
65 69 64,5-69,5
67 5 10 0,1 10 20
70 74 69,5-74,5, 72 8 18 0,16 16 36
75 79 74,5-79,5
77 12 30 0,24 24 60
80 84 79,5-84,5
82 16 46 0,32 32 92
85 89 84,5-89,5 87 4 50 0,08 8 100
50 1,0 100

32. 59,5- 64,5
60 64 62 5 5 0,1 10 10
65 69 64,5-69,5 67 5 10 0,1 10 20 ³ 30%
70 74 69,5-74,5, 72 8 18 0,16 16 36
75 79 74,5-79,5
77 12 30 0,24 24 60
80 84 79,5-84,5 82 16 46 0,32 32 92
85 89 84,5-89,5 87 4 50 0,08 8 100
64%
¿ Cuánto alumnos obtuvieron 69 o menos punto ?
¿ Qué % obtuvo 75 o más puntos ?
¿ Cuántos alumnos obtuvieron entre 80 y 84 puntos ?
¿ En cuales clases se concentraron la mayoría de los puntajes ,
entre puntos estuvieron y a que % corresponde ?
75 y 84 puntos 56 %

33. GRÁFICOS
Los gráficos nos permiten obtener
información de forma ordenada y
resumida sobre las variables en estudio.
Los gráficos más utilizados son:
a) Gráfico de barra: Es un diagrama de
barras rectangulares, cuya altura de
cada barra indica la frecuencia absoluta
de cada valor de la variable.

34. Las barras pueden estar orientadas en
forma horizontal o vertical. Estos
gráficos se usan para comparar dos o
más valores. Este gráfico sirve para
representar variables cualitativas y
cuantitativas.

35. Ejemplo 1:

36. Ejemplo 2:
cantidad de personas arriba de un avión
60
50
40
Cantidad
30 Serie1
20
10
0
HOMBRES MUJERES
Género

37. b) Gráfico Circular: Es un gráfico formado
por un círculo dividido en sectores. Se
utiliza para representar cualquier tipo de
frecuencias aunque, generalmente, se
utiliza para frecuencias relativas
porcentuales. Este gráfico sirve para
representar variables cualitativas y
cuantitativas.

38. Ejemplo 1:
Deportes Preferidos
Bicicleta
Nadar
Trotar
Fútbol
21%
41%
24%
12%

39. Histograma: Es un gráfico cuya altura es
proporcional a la frecuencia absoluta,
frecuencia relativa o frecuencia
porcentual, y la base está formada por
segmentos cuyos extremos representan
los extremos de cada intervalo. Este
gráfico sirve para representar variables
cuantitativas.

40. 45 17 - 20
13 - 16
40
35
30 5-8
25 5-8 9 - 12
20 9 - 12 13 - 16
15 17 - 20
10
5
0
1

41. Polígono de Frecuencias: Se obtiene al
unir los puntos medios de los intervalos
representados por cada barra de un
histograma, es decir, al unir la marca de
clase de cada intervalo mediante una
línea poligonal.

42. Edad de los estudiantes
45
40
35
N° de estudiantes
30
25
Serie2
20
15
10
5
0
5-8 9 - 12 13 - 16 17 - 20
Años

43. Medidas de tendencia central
Las medidas de tendencia central,
denominados también PROMEDIOS,
ubican el centro de los datos, como la
media aritmética, la media geométrica,
la media armónica y la mediana.
Las cuales serán calculadas para datos
NO agrupados y agrupados (tabla de
frecuencia)

44. MEDIA ARITMÉTICA O
PROMEDIO ARITMÉTICO
SE SIMBOLIZA POR X
SE CALCULA SUMANDO LAS
OBSERVACIONES x1, x 2 , x 3 ,...... x n
Y SE DIVIDE POR POR EL NÚMERO
TOTAL DE ELLAS , O SEA :
x1 + x 2 + x 3 + .... x n
X=
n

45. MEDIANA
ES EL VALOR CENTRAL DE UNA
DISTRIBUCIÓN ORDENADA DE
MENOR A MAYOR O VICEVERSA , QUE
DEJA SOBRE Y BAJO SI , EL 50 % DE
LOS VALORES DE LA DISTRIBUCIÓN,
SE SIMBOLIZA POR :
Me

46. EJEMPLO :
2 4 6 7 9 12 16
MENORES MAYORES
MEDIANA
Me = 7

47. SI EL NÚMERO DE DATOS ES PAR
LA MEDIANA ES IGUAL A LA MEDIA ARITMÉTICA
DE LOS DOS VALORES CENTRALES
EJEMPLO :
5 8 10 13 15 18
10 + 13
x=
ˆ = 11,5
2

48. MODA
EN LENGUAJE COTIDIANO LO QUE
ESTÁ DE MODA ES LO QUE MAS SE
LLEVA, LOQUE MAS SE USA .
MODA : ES EL VALOR CON MAYOR
FRECUENCIA , SE DESIGNA
POR : Mo

49. PUEDE HABER MAS DE UNA MODA O
NO HABER MODA
EJEMPLO
1122233444455566667788
9
HAY DOS MODAS 4 Y 6
335566778899
EN ESTE CASO NO HAY MODA

50. EJEMPLO
EN EL CONJUNTO DE LOS DATOS :
5 2 2 2 4 5 6 6 6 6 7 7 8 9
LA MODA ES : Mo = 6
La moda es el promedio menos importante
por su ambigüedad

51. Medidas de tendencia central para
datos agrupados.
Media o Media aritmética: Si n valores de
alguna variable X están tabulados en
una distribución de frecuencias de
intervalos, donde:
y1 , y 2 , y 3 ,..., y k son las marcas de clases, luego
f 1 , f 2 , f 3,..., f k son las frecuencias absolutas respectivas,

52.  Entonces su media aritmética está dada
por:
k
∑f i ⋅ mi
x= i =1
n

53. Mediana para Datos Agrupados
 Está dada por la fórmula:
n
− Fi −1
Me = Li + 2 ⋅A
fi

54.  Dónde
Li : Límite inferior de la frecuencia acumulada, inmediatamente
posterior al 50%
n: Cantidad total de datos
Fi −1 : Frecuencia acumulada anterior a la mediana
fi : Frecuencia absoluta del intervalo de la Mediana

55. Ejemplo
Edades Número de Frecuencia
 Ingreso de personas Personas Acumulada
a U.C.I coronaria de 26 – 33 1 1
un determinado 34 – 41 2 3
Hospital 42 – 49 4 7
n
− Fi −1 50 – 57 10 17
Me = Li + 2 ⋅A 58 – 65 16 33
fi 66 – 73 8 41
74 – 81 3 44
82 - 89 1 45

56. Moda para datos agrupados
 Para calcular la moda tabulados por
intervalos, primero se determina el
intervalo que contiene la moda, esto es,
el intervalo que tiene la mayor
frecuencia (intervalo modal). Luego se
utiliza la fórmula
 d1 
Mo = Li + 
d +d ⋅ A

 1 2 

57. Donde:
Li = Límite inferior del intervalo modal
d1 = f i − f i −1 esto es igual a la
frecuencia del intervalo modal menos la
frecuencia del intervalo inmediatamente
anterior

58. d 2 = f i − f i +1 Esto es igual a la
frecuencia del intervalo modal menos la
frecuencia del intervalo inmediatamente
posterior
A = Amplitud

59. Del ejemplo anterior
Edades Número de Personas Frecuencia
Acumulada
26 – 33 1 1
34 – 41 2 3
42 – 49 4 7
50 – 57 10 17
58 – 65 16 33
66 – 73 8 41
74 – 81 3 44
82 - 89 1 45

60.  6 
Mo = 58 +  ⋅7 =
 6+8
58 + 0,429 ⋅ 7 =
60,996 ≈ 61

61. Cuartiles, Deciles y Percentiles
 Si un conjunto de datos se ordena de
acuerdo con su magnitud, el valor
central que divide al conjunto en dos
partes iguales es la MEDIANA.
Extendiendo esta idea, es posible
considerar los valores que dividen al
conjunto en cuatro, diez o cien partes
iguales

62. Fórmula general
% ⋅ n − N i −1
Li + ⋅ ( Ls − Li )
fi

63. Donde:
Li : Límite inferior de la clase utilizada
% : Porcentaje a utilizar, expresado cómo
número racional (Dividir en 100)
n : Número total de datos de la muestra

64. N i −1 : Frecuencia acumulada anterior
f i : Frecuencia absoluta de la clase
utilizada
Ls : Límite Superior de la clase utilizada

65. Ejemplo 1
Peso M. Clase Fr. Fr. ac.
40 – 49 45 5 5
50 – 59 55 10 15
60 – 69 65 21 36
70 - 79 75 11 47
80 - 89 85 5 52
90 - 99 95 3 55
100 – 109 105 3 58
58
0,75 ⋅ 58 − N i −1 43,5 − 36
P75 = Li + ( Ls − Li ) = 70 + (79 − 70) = 76,13
fi 11

66. Ejemplo 2:
Salarios N° Empleados
 La siguiente tabla muestra
una distribución de
frecuencia de salarios 250.000 – 259.999 8
semanales de 65 empleados
de una determinada 260.000 – 269.999 10
empresa.
270.000 – 279.999 16
Calcule: el cuartil 3, los 280.000 – 289.999 14
deciles 2, 4,7 y 9 y los
percentiles 7, 19, 48, 67, 79 290.000 – 299.999 10
300.000 – 309.999 5
310.000 – 319.999 2

67. Medidas de dispersión
 Son números que miden el grado de
separación de los datos con respecto a
un valor central. (Generalmente la
media)
Estudiaremos las dos más importante:
c) Varianza
d) Desviación Estándar

68. Varianza
 Es la media aritmética de los cuadrados
de las diferencia de los datos con
respecto a su media aritmética. Está
dada por la fórmula:
n
∑ (x i − x) 2
s =
2 i =1
n

69. Ejemplo 1: (Datos no
agrupados)
 Obtener la varianza de los siguientes
valores:
1,3,3,5,7,18,10

70. Varianza para datos AGRUPADOS
n
∑ f ( x − x)
i i
2
s =
2 i =1
n