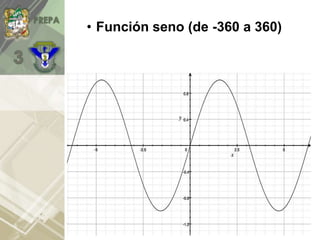
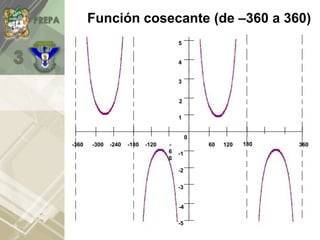
Este documento presenta un tema sobre gráficas de funciones trigonométricas. Explica definiciones básicas como el círculo unitario y valores de funciones como seno, coseno, tangente para ángulos de 0 a 360 grados. También muestra gráficas de estas funciones y cómo varían periódicamente, así como aplicaciones en la resolución de triángulos rectángulos.