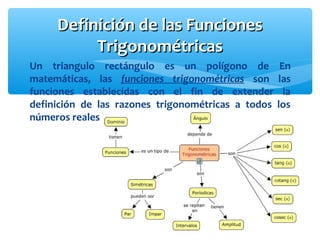
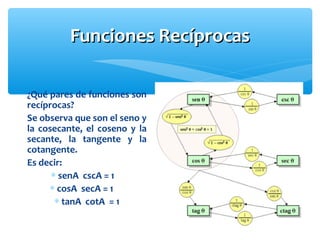
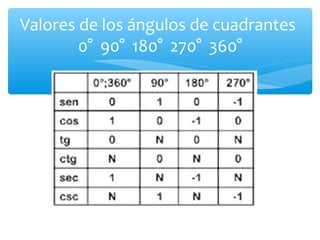
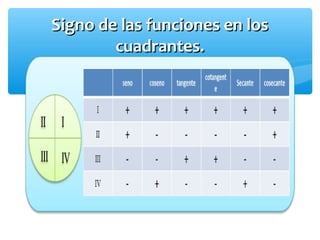
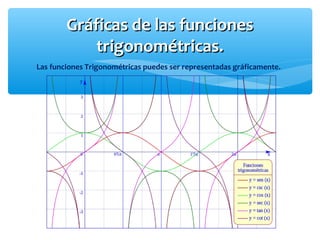
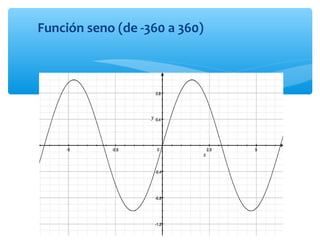
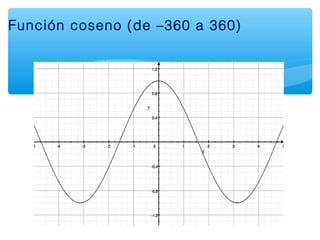
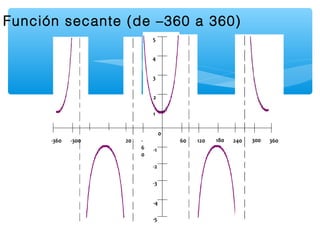
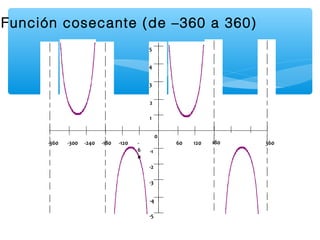
Este documento presenta los conceptos básicos de la trigonometría. Explica las definiciones de las funciones trigonométricas, funciones recíprocas, complementarias y sus gráficas. También cubre valores de ángulos especiales, cuadrantes y la resolución de triángulos rectángulos.

1. FUNCIONESFUNCIONES
TRIGONOMÉTRICASTRIGONOMÉTRICAS
PEDRO ALEXISPEDRO ALEXIS
Universidad de PanamáUniversidad de Panamá
Campo virtualCampo virtual

2. 1. Conceptos básicos del triángulo rectángulo ( lados y
ángulos )
2. Definición de las Funciones Trigonométricas
3. Funciones Recíprocas
4. Funciones Complementarias
5. Valores de los ángulo especiales 30° 45° 60°.
6. Valores de los ángulos de cuadrantes 0° 90° 180° 270°
360°
7. Signo de las funciones en los cuadrantes.
8. Gráficas de las funciones trigonométricas.
9. Dado el valor de una función trigonométrica. Hallar el
valor de Las otras.
10. Resolución de triángulo rectángulo.
PLAN DE TRIGONOMETRÍAPLAN DE TRIGONOMETRÍA

3. Conceptos básicos del triánguloConceptos básicos del triángulo
rectángulo ( lados y ángulos )rectángulo ( lados y ángulos )
1. Un triangulo rectángulo es un polígono de tres lados con un
ángulo recto (90°) y dos ángulos agudos que son
complementarios (suman 90°).
2. Hipotenusa, es el lado mayor del triangulo.
3. Cateto, son los lados menores que forman el ángulo recto.
4. Un ángulo agudo esta formado por la hipotenusa y un cateto.
5. Cateto adyacente a un ángulo agudo, es el que forma el
ángulo.
6. Cateto opuesto a un ángulo agudo, es el que no forma el
ángulo.
7. Es importante observar "todo lado opuesto a un ángulo
agudo es adyacente del ángulo complementario", "todo lado
adyacente a un ángulo agudo es opuesto del ángulo
complementario".

4. Definición de las FuncionesDefinición de las Funciones
TrigonométricasTrigonométricas
Un triangulo rectángulo es un polígono de En
matemáticas, las funciones trigonométricas son las
funciones establecidas con el fin de extender la
definición de las razones trigonométricas a todos los
números reales y complejos.

6. Funciones RecíprocasFunciones Recíprocas
¿Qué pares de funciones son
recíprocas?
Se observa que son el seno y
la cosecante, el coseno y la
secante, la tangente y la
cotangente.
Es decir:
∗ senA cscA = 1
∗ cosA secA = 1
∗ tanA cotA = 1

7. Funciones ComplementariasFunciones Complementarias
¿Qué pares de funciones son complementarias?.
Se observa que son seno y coseno, tangente y
cotangente , secante y cosecante.
Es decir,, s i A y B son ángulos complementarios
entonces:
∗senA = cosB
∗tanA = cotB
∗secA = cscB

8. Valores de los ángulo especialesValores de los ángulo especiales
0° 30° 45° 60° 90°0° 30° 45° 60° 90°
Valores de Ángulos Especiales 0° 30° 45° 60° 90°
Presentar el cuadro de estos ángulos

9. Valores de los ángulos de cuadrantes
0° 90° 180° 270° 360°

10. Signo de las funciones en losSigno de las funciones en los
cuadrantes.cuadrantes.

11. Gráficas de las funcionesGráficas de las funciones
trigonométricas.trigonométricas.
Las funciones Trigonométricas puedes ser representadas gráficamente.

12. Función seno (de -360 a 360)

13. Función coseno (de –360 a 360)

14. Función tangente (de –360 a 360)
300-
60
-120-180-240-300-360 36060 120 180 240
0
1
2
3
4
5
-1
-2
-3
-4
-5
300

15. -
6
0
-120-180-240-300-360 36060 120 180 240
0
1
2
3
4
5
-1
-2
-3
-4
-5
300
unción cotangente (de –360 a 360)

16. -
6
0
-120-180-240-300-360 36060 120 180 240
0
1
2
3
4
5
-1
-2
-3
-4
-5
300
Función secante (de –360 a 360)

17. -
6
0
-120-180-240-300-360 36060 120 180 240
0
1
2
3
4
5
-1
-2
-3
-4
-5
300
Función cosecante (de –360 a 360)

18. ∗ Ejemplo 1: tanA = ¾. Aplicando el Teorema de Pitágoras
c = √32
+ 42
= 5
senA = 3/5 cosA = 4/5 tanA =3/4
cotA = 4/3 secA = 5/4 cscA = 5/3
∗ Ejemplo2 cosA = 5/13 Aplicando el Teorema de Pitágoras
a = √ 132
- 52
= 12
senA = 12/13 cosA = 5/13 tanA = 12/5
cotA = 5/12 secA = 13/5 cscA = 13/12
Dado el valor de una funciónDado el valor de una función
trigonométrica.trigonométrica.
Hallar el valor de Las otras.Hallar el valor de Las otras.

19. Para resolver un triángulo se necesita conocer tres
elementos de los cuales uno debe ser un lado. En el
caso del triángulo rectángulo hay un elemento ya dado
que es el ángulo recto (90°)
Caso 1. Dado un lado y un ángulo, ejemplos:
Lado a = 15; ángulo b = 36°. Lado b = 10; ángulo a = 52°
Caso 2. Dado dos lados, ejemplos:
Lado a = 12, lado c =20. Lado b = 64; lado a =37
Resolución de triángulo rectánguloResolución de triángulo rectángulo

20. GRACIASGRACIAS