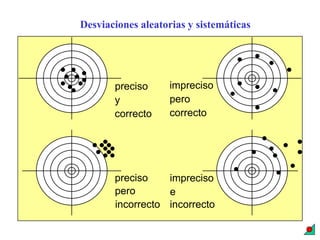
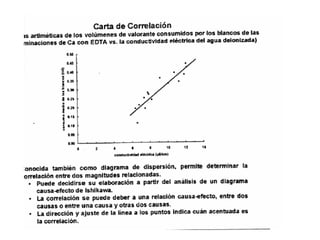
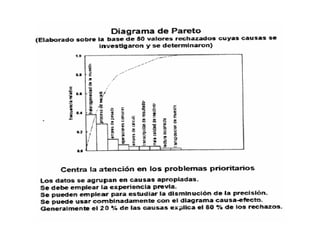
Este documento describe conceptos clave relacionados con la medición y el control de calidad. Explica que una medida nunca es perfectamente precisa respecto al valor verdadero debido a limitaciones inherentes. También describe cómo se usan muestras de control de calidad, materiales de referencia certificados y gráficos de control para monitorear la precisión y exactitud de un proceso de medición.

1. Una medida es sólo
una estimación porque todas
las medidas tienen limitaciones
en la presición respecto al valor
verdadero
Aún cunado calibramos y
trabajamos con las mejores
prácticas de calidad tenemos
Incertidumbre en nuestras
medidas respecto al
Valor verdadero
Valor verdadero es un concepto teórico

2. Valor verdadero (de una
magnitud):
Valor consistente con la definición de una magnitud
en particular.
• Es el valor que se obtendría en una medida
perfecta
• Los valores verdaderos son por naturaleza
indeterminados
(El prototipo de la masa tiene incertidumbre cero, las
demás magnitudes se miden, por lo tanto, no
tienen incertidumbre cero).

3. Valor de referencia aceptado
(VRA) o valor verdadero:
valor que sirve como una referencia y
proviene de:
1) un valor teórico o establecido
2) un valor asignado basado en trabajo
experimental de una organización, ej.:NIST
3) un valor consensuado, basado en trabajo
experimental colectivo

4. • Exactitud ( accuracy)
Grado de concordancia entre el resultado de un
ensayo y el valor verdadero.
Es un concepto cualitativo.
Cuando se aplica a un conjunto de resultados de
mediciones involucra la combinación de los
componentes aleatorios y de error sistemático
 Error de una medida
Resultado de una medición menos el valor verdadero
de una magnitud a medir.
Es un concepto cuantitativo.

5. Veracidad (trueness)
Grado de concordancia entre el valor
promedio obtenido de una serie de
resultados del ensayo y el valor verdadero.
Es el concepto cualitativo asociado al sesgo.
• Sesgo o error sistemático (bias):
Error sistemático que contribuye a la
diferencia entre el valor promedio de una
población de resultados y el valor verdadero
Si es importante se puede aplicar una
corrección..

6. Inestabilidad del instrumento
Contaminaciones Fluctuaciones
variables ambientales
Instrumento
Errores sistemáticos Analista
Procedimiento
Efecto de matriz analítico
Blanco
Ineficiencias,
pérdidas

7. Inestabilidad del instrumento
Contaminaciones Fluctuaciones
variables ambientales
Inestabilidad del
Instrumento Habilidad
Errores aleatorios del Analista
Procedimiento
Efecto de matriz analítico
Control Variabilidad
De reactivos de los blancos
Pérdidas variables

8. Inestabilidad del instrumento
Cambio paulatino Modificación
de la humedad de una fuente
ambiental de excitación
o de la Errores por falta
temperatura de control
Variaciones
en el ajuste
Hidrólisis parcial óptico o
mecánico
Oxidación paulatina Evaporación del
de la muestra solvente

9. Lectura equivocada
Muestra Transposición
equivocada transcripción
Contamina
ción grosera Calibración
incorrecta
Pérdidas
Falta de
control
Error de cálculo estadístico
Procedimiento Muestreo
erróneo incorrecto
Errores ilegítimos

10. Precisión
La concordancia entre resultados mutuamente
independientes obtenidos en condiciones
preestablecidas.
Está asociada a la dispersión de los resultados
La precisión es atribuida a valores aleatorios
inevitables inherentes a cada procedimiento de
medición y no se relaciona al valor verdadero.

11. Desviaciones aleatorias y sistemáticas
preciso
y
correcto
impreciso
pero
correcto
preciso
pero
incorrecto
impreciso
e
incorrecto

12. Repetibilidad
 Precisión bajo condiciones en las que los
resultados de las mediciones mutuamente
independientes son obtenidas con el mismo
método, en el mismo laboratorio, por el
mismo operador, con el mismo equipo
dentro de intervalos cortos de tiempo,
usando alícuotas de una misma muestras

13. Reproducibilidad
• Precisión bajo condiciones en las que los
resultados de una medición son obtenidos
usando el mismo método usando material
de ensayo idéntico, en diferentes
laboratorios, con operadores y equipos
diferentes.

14. Precisión intermedia
(usualmente reproducibilidad
intermedia o local)R´
Precisión en condiciones intermedias entre
repetibilidad y reproducibilidad. Por
ejemplo, precisión con el mismo método,
diferentes operadores, diferentes
instrumentos y durante un intervalo de
tiempo largo en el mismo laboratorio

15.  Causa asignable:
Factor que contribuye a la variación de un
resultado y que es factible de detectar e
identificar
 Causa aleatoria:
Una causa individual entre varias, de
relativa poca importancia que contribuye a
la variación y que no es factible de
identificar o aislar

16. Técnicas diversas de Control de Calidad

23. Sistema de aseguramiento de la calidad
debe (en lo posible) incluir:
• Programa de calibración del equipamiento
y registro histórico del mismo
• Gráficos de control para controlar
estabilidad y precisión
• Comparaciones interlaboratorios
• Auditorias de métodos

24. Control estadístico de los
procesos
• Se logra cuando los valores de un conjunto
relativamente elevado de mediciones
manifiestan una tendencia central y su
dispersión puede caracterizarse
cuantitativamente

25. Causas asignables y causas
aleatorias de la variación de
calidad
• Un proceso que está operando con variabilidad
debido a solamente causas aleatorias se dice que
está bajo control estadístico
• Si está operando bajo condiciones de variabilidad
debido a causas asignables se dice que está fuera
de control
• El objetivo del control estadístico de procesos es
reducir la variabilidad identificando las causas
asignables

26. Evaluación de la precisión y
exactitud de los métodos
 Controlar periódicamente estabilidad y precisión
con una Muestra de Control de Calidad (MCC)
 Controlar periódicamente exactitud con un
estándar o Material de Referencia
Certificado(MRC)
 Intervenir en ensayos de aptitud o ensayos
interlaboratorios
 Validar independiente y periódicamente con
muestras de auditoria de evaluación

27. Muestra de Control de Calidad
(MCC)
Una MCC es una cantidad de material que se
ha separado del resto de las muestras, para
efectuar mediciones periódicas de un
parámetro, con el propósito de controlar el
proceso de medición.

28. Muestra de Control de Calidad
(MCC) (2)
• Criterios de selección:
 Similar a la muestra de rutina
 Estable
 Homogénea
 Valor más probable conocido o determinado
por análisis repetidos
 cantidad suficiente para 6 meses o un año
• Almacenada para preservar las propiedades a
medir

30. Gráficos de control
Representaciones gráficas de datos de acuerdo a
determinadas reglas de construcción que permiten:
 Demostrar el estado de control estadístico del
sistema analítico
 Seguimiento de un proceso de medición
 Diagnosticar problemas de medición
 Documentar la incertidumbre de los resultados

31. Gráficos de control
Son efectivos para prevenir desviaciones
Previene ajustes innecesarios
En el caso de usarse para control de
procesos, mejora la productividad
Provee información acerca de la capacidad
del proceso: capacidad de determinar
conformidad con las especificaciones

32. Incertidumbre y límites de aceptación:
Límite
Superior de
Control
?
?
1.
2.
4.
3.

33. Principios de construcción de
gráficos de datos individuales
Suposiciones:
Población normal
Son desconocidas y
(o se estiman previamente)
 Sus estimadores experimentales son y
s
Cuando se emplea material de referencia
certificado (MRC), - XMRC estima el
sesgo
 x
x
x

34. Distribución normal
Frecuencia

35. LCS
LAS
Línea 6S
central
LAI
LCI
x

36. Gráficos de control
• Principios básicos
Un gráfico de control típico tiene límites de control
tales que si el proceso está bajo control,
prácticamente todos los puntos estarán entre el
límite superior y el inferior
• Situaciones fuera de control
 Si por lo menos un punto queda fuera de los
límites de control: proceso fuera de control
 Si los puntos se comportan de una manera
sistemática: proceso fuera de control

37. Programa de construcción del
gráfico:
• Frecuencia depende de :
 uso
Importancia del parámetro
Información histórica de estabilidad y
precisión
Costo
Requerimiento del método, o legal o
contractual

38. Programa de construcción del
gráfico:
Establecer un protocolo de modo que todas
las personas que rutinariamente realizan el
ensayo participen en generar datos para el
gráfico
Tratamiento de la MCC similar a las
muestras analizadas rutinariamente
Realizar los ensayos de la MCC en horas al
azar dentro de las horas que se analiza
habitualmente

39. Tratamiento de datos
Pretratamiento
Objetivo: Normalizar las escalas de los
gráficos de control de modo de representar
en el mismo gráfico datos de estándares
diferentes
• MCC : En general no se representa en el
mismo gráfico resultados de MCC distintos

40. Tratamiento de datos
• Estándares
 Lotes con igual VRA y con precisión
constante en todos los niveles:
Resultado pretratado= Resultado del ensayo - VRA
Lotes con distinto VRA y con precisión
variable según el nivel:
Resultado pretratado= Resultado del ensayo - VRA
a ese nivel

41. Gráfico de control I
Indicaciones generales para construir gráfico
de control simple
1. Seleccionar método para adquirir los datos
aleatoriamente
2. Obtener los datos y realizar la gráfica de
corrida
3. Examinar los datos:
a) identificar y descartar datos erróneos
b) identificar y descartar patrones inusuales
c) comprobar distribución normal

42. Test para chequear normalidad
• Construir la gráfica de probabilidad normal
Si los resultados muestran desviación obvia
de la normalidad, las técnicas estadísticas de
gráficos de control no son aplicables
directamente. Se deben hacer
transformaciones.

43. Test para comprobar la Normalidad
X Xi ascendente
i
N+1
zi
58.2 48.3 0.1 -1.28
52.7 49.4 0.2 -0.84
48.3 51.3 0.3 -0.52
52.7 52.7 0.4 -0.25
49.4 52.7 0.5 0.00
53.2 53.2 0.6 0.25
55.1 55.1 0.7 0.52
51.3 55.2 0.8 0.84
55.2 58.2 0.9 1.28

44. -1,5
-1
-0,5
0
0,5
1
1,5
48 49 50 51 52 53 54 55 56 57 58
xi
zi
i/(n+1)
Zi
z
i/(n+1)
Es la probabilidad normal
acumulada

45. Gráfico de control I
n
x
n
i
ix
 1
SXLCS 3
SXLCI 3
SXLAS 2
SXLAI 2
4. Calcular la media aritmética y límites de control y
de alerta

46. Gráfico de control I
4. Con 15 a 20 puntos dibujar gráfico de control
5. Revisar los datos y excluir valores anómalos
5. Rechazar los valores y patrones anómalos
6. Redibujar el gráfico si es necesario
7. Dibujar el histograma
7. Si no se dispone de una MCC estable, y se está
usando una MRC, se puede usar el valor
certificado como media

47. Comportamientos anormales
• Zona de peligro: entre 2s y 3s (entre LA y
LC)
• Zona b: entre s y 2s
• Zona c: entre línea central y s
1) Un punto afuera de los límites de control
(3s)
2) Si hay dos de tres datos consecutivos en la
zona de peligro en la misma dirección:

48. Comportamientos anormales
Ha aparecido un sesgo de largo término si:
3) 5 datos consecutivos están fuera de los
límites de desviación (1s) en la misma
dirección
4) 9 o más puntos alineados por encima o
debajo de la línea central
5) 7 puntos alineados en dirección creciente o
decreciente

49. Comportamientos anormales
Reglas para el histograma
Si la distribución de datos es en forma de
campana pero no es 66% dentro de los
límites de desviación, 95% dentro de los de
advertencia y 99% dentro de los de acción:
• Distribución estrecha
• Distribución ancha

50. Comportamientos anormales
• Si la distribución es bimodal : diferentes
analistas
• Si es distorsionada: puede deberse a un
sesgo subjetivo en la forma en que se
generan los datos (por ej. Tendencia a
terminar antes una titulación)

51. Interpretación de los gráficos de
control
Aplicar las reglas para determinar si los
datos corroboran la hipótesis que el sistema
de medición está bajo control estadístico
Investigar los puntos fuera de control
estadístico. Si se encuentra una causa
asignable dejarlo claramente registrado
Todos los datos deben quedar registrados

52. Actualización de Gráficos de Control:
(1)cuando no hay modificaciones en el sistema
 Cuando estén disponibles por lo menos 15 nuevos
datos bajo control estadístico, recalcular la
estimación de la precisión: realizar antes un test F
para la varianza de las muestras
 Si resulta que la diferencia de varianzas no son
significativas: recalcular la varianza con todos los
datos (ver combinación de varianzazas)
 Si resulta que la diferencia es significativa realizar
una investigación de causas asignables

53. Actualización de Gráficos de Control
(2) Cuando ocurre un cambio en el nivel de la MCC
debido a una causa asignable por cambio de
muestra
 Tomar un nuevo lote del material en estudio
cuando no se dispone para más de 20
determinaciones de la MCC.
 Realizar análisis simultáneos y registrar los datos
de la nueva MCC cada vez que se realice de la
MCC vigente.
 Iniciar un gráfico I para la nueva MCC después de
15 puntos en control estadístico

54. Gráficos de Rango Móvil
El rango móvil (RM) se define como la
diferencia absoluta entre dos observaciones
sucesivas:
RM=
el cual indica posibles desviaciones o
cambios en el proceso de una observación a
la siguiente
xx ii 1


55. Gráficos I y de Rango Móvil
El gráfico de X es de datos individuales. Los
límites de control son:
d2= 1.128 para
m>20
donde
2
2
3
3
d
MR
xLCI
xLC
d
MR
xLCS



m
MR
MR
m
1i
i
 

56. Gráficos I
Desviación estándar local :
77.2
`
`
RsR


57. Comparación de R`con la RASTM
• Se compara la Reproducibilidad local con la
Reproducibilidad del método ASTM para el
mismo nivel, usando el test c2.
• La Reproducibilidad local debe ser menor o
igual a la de ASTM.

58. Gráficos de tendencia (EWMA)
• Se construye a partir de los datos individuales para
aumentar la sensibilidad, para detectar
apartamientos pequeños en relación a la precisión
del sistema
• La línea de tendencia se superpone al gráfico I.
• Cada punto EWMA es un promedio ponderado del
resultado obtenido y del resultado previo, con el
peso decreciendo exponencialmente con la edad
de la lectura.

59. Gráficos de tendencia (EWMA)
• La secuencia de valores se obtienen según:
Donde 0 <   1 es el factor de ponderación exponencial.
Se recomienda un factor de 0.4 o 0.2.
• Se parte de z0 =
• Una línea de tendencia diseñada adecuadamente es
menos sensible a la suposición de normalidad
1iii z)1(xz 
1x

60. Gráficos de tendencia (EWMA)
• Los límites de control para la línea de
tendencia son:
)2(
66.2
)2(
66.2
0
0
0












MRLCI
LC
MRLCS
)2(
66.2
)2(
66.2
0
0
0












MRLCI
LC
MRLCS

61. Gráficos de tendencia (EWMA)
• Para 0.2:
sxLCS 
sxLCI 

62. Gráficos de control de la media
aritmética
• Los gráficos de control dependen de la suposición
de normalidad
• El Teorema central del límite permite asumir la
suposición de normalidad con mayor seguridad
• La distribución de las medias es más normal que
la de los valores individuales
• Muchas causas de variación que no son
dominantes tienden hacia poblaciones
normalmente distribuidas

63. Gráficos de control de la media aritmética
• Controlan la constancia en la media y la precisión
• Los datos se agrupan en subgrupos racionales: se
repite el ensayo manteniendo todas las mismas
condiciones excepto un parámetro. Generalmente
se usan subgrupos de 5 datos
• Debe haber eventualmente la máxima diferencia
entre grupos
• La variabilidad tolerada en el proceso es la
existente dentro de cada subgrupo racional

64. Gráficos de control de la media aritmética
• Se determina el s para cada subgrupo y
luego se calcula:
n
sss
s nBA
222
2 ...

sxLCI
xLC
sxLCS
3
3




65. Para evaluar la exactitud del
sistema analítico:
• Se realizan por lo menos 15 medidas con un
estándar o material de referencia certificado
• Graficar las diferencias individuales con el
VRA
• Realizar un test t para determinar si el
promedio de las diferencias es
estadísticamente distinto de cero

66. Generalidades sobre el uso del gráfico de
control
 Considerar al gráfico de control como una
herramienta para mejorar el proceso de análisis
 Graficar los datos a medida que se generen
 Considerar todos los componentes del sistema
cuando se investiga un problema:
• si hay algo roto, descentrado, etc
• si los reactivos están en condiciones de uso
• si se siguen todos los pasos del método
• si el medio cambió (calor, frío, humedad)
• si los técnicos están adecuadamente entrenados
• si la MCC está todavía estable

67. Generalidades sobre el uso del gráfico de
control
 Tomar acciones correctivas y documentar los
puntos clave
 Utilizar la sección de observaciones del gráfico
para señalar:
• cambio de condiciones y reactivos
• mantenimientos y calibraciones programadas y no
programadas
• observaciones inusuales
• acciones correctivas de puntos fuera de control