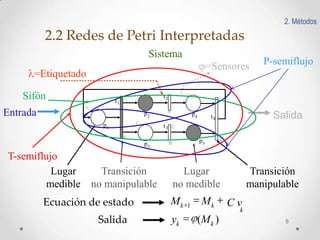
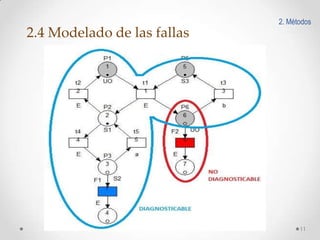
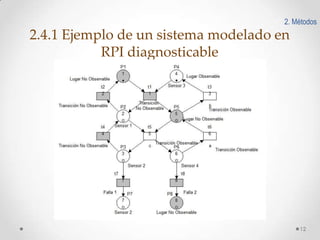
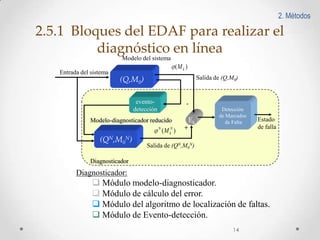
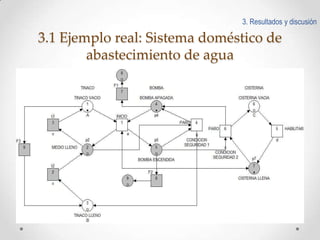
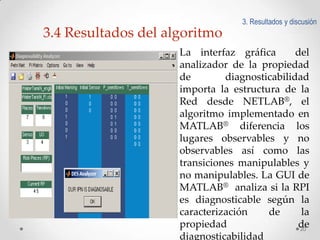
Este documento presenta un esquema de detección y aislamiento de fallas utilizando redes de Petri interpretadas y Matlab. El esquema incluye modelar el sistema y las fallas usando redes de Petri, obtener las estructuras matemáticas de la red, implementar un algoritmo de detección de fallas en Matlab, y simular el comportamiento del sistema y la detección de fallas en línea. Se provee un ejemplo de aplicación al sistema de abastecimiento de agua doméstico.

1. Esquema de detección y aislamiento de
fallas utilizando Matlab®
Autores:
MC. Alejandro Javier Arredondo García
Dra. Elvia Ruiz Beltrán
Dr. Jorge Luis Orozco Mora
Aguascalientes, Ags., Mayo de 2013

2. Contenido
1. Introducción
2. Métodos
3. Resultados y discusión
4. Conclusión
5. Referencias
2

3. 1. Introducción

4. 1. Introducción
1.1 Estado actual del tema
• En la actualidad los sistemas a controlar son más
complejos
debido
a
que
deben
satisfacer
especificaciones con un alto grado de desempeño.
•La implementación de un esquema de localización y
detección de fallas resulta de gran interés en el diseño
de sistemas de producción.
•Matlab® es una herramienta que permite simular
esquemas de detección de fallas y ayuda a determinar
su efectividad.
•La implementación del esquema propuesto pretende
ser una herramienta de desarrollo en el área de
diagnóstico de fallas.
4

5. 1. Introducción
1.2 Antecedentes
• Enfoques: Autómatas finitos (AF), Redes de Petri (RP)
Autómatas Finitos
Diagnosticadores que
toman en cuenta la
alcanzabilidad del
esquema propuesto
Redes de Petri
Diagnosticadores basados en la estructura
matemática de la red
[Giúa y Seatzu,’01],[Dotoli,’09],[Basile,’09],
[Ramírez-Treviño, Ruiz-Beltrán ,’07,‘11]
[Sampath, ‘95, ‘96]
Diagnosticador: AF obtenido del
modelo del sistema
• Propiedad Diagnosticabilidad
• Capaz de realizar un diagnóstico en
línea
5

6. 2. Métodos

7. 2.1 Metodología
2. Métodos
1) Se analiza la estructura de sistemas modelados a partir de
una metodología de modelado ascendente (de una red
particular a una general) que arroja modelos de RPI vivos,
fuertemente conexos y binarios.
2) Se representan las fallas permanentes y operacionales en
el modelo de RPI
3) A
partir de Netlab® se obtienen las estructuras
matemáticas importantes de la red para su análisis en el
EDAF : la matriz de Incidencia(C) y la matriz que asocia
los sensores a los lugares (φ) en los estados de interés.
4) Matlab® como herramientas para la implementación del
EDAF, permite el análisis de la estructura de la red y la
simulación de su comportamiento en línea.
7

8. 2. Métodos
2.2 Redes de Petri Interpretadas
Sistema
=Sensores
=Etiquetado
Sifón
Entrada
A
a
p2
p1
C
T-semiflujo
Lugar
Transición
medible no manipulable
Salida
p4
Salida
t4
t3
p3
Ecuación de estado
B
t2
t1
P-semiflujo
p5
b
c
Lugar
no medible
Mk
yk
1
Mk
(M k )
Transición
manipulable
Cv
k
8

9. 2. Métodos
2.4 Caracterización de la diagnosticabilidad
en RPI
N
N
Sea (Q, M 0 )
una RPI binaria, donde (Q , M 0 ) es viva y
fuertemente conexa. Las fallas han sido modeladas con la
metodología descrita, en donde para cualquier transición t f ,
todas las transiciones en TfR , TfPRson evento detectables y al
path
menos una transición t z de cada secuencia
Tf es evento
detectable y
, Si N f es igual a (Q N , M 0N ) , entonces
la red es diagnosticable.
10

10. 2. Métodos
2.4 Modelado de las fallas
11

11. 2. Métodos
2.4.1 Ejemplo de un sistema modelado en
RPI diagnosticable
12

12. 2. Métodos
2.5 Esquema de detección y aislamiento de
faltas (EDAF)
• Una vez que la red cumple la caracterización de
diagnosticabilidad, es posible detectar en línea en
un tiempo finito las faltas permanentes y
operacionales que se presenten.
• La importancia de este esquema radica en que es
posible no solo conocer las faltas sino además es
posible aislarlas y saber a qué conjunto de faltas
pertenece.

13. 2. Métodos
2.5.1 Bloques del EDAF para realizar el
diagnóstico en línea
Modelo del sistema
(M k )
Entrada del sistema
Salida de (Q,M0)
(Q,M0)
eventodetección
-
N
(QN,M0N)
( M kN )
+
Modelo-diagnosticador reducido
Ek
Detección
de Marcados
de Falta
Estado
de falla
Salida de (QN,M0N)
Diagnosticador
Diagnosticador:
 Módulo modelo-diagnosticador.
 Módulo de cálculo del error.
 Módulo del algoritmo de localización de faltas.
 Módulo de Evento-detección.
14

14. 2. Métodos
2.5.2 Etapas del esquema propuesto
• Sistema: Se obtienen las estructuras importantes
de Red C, ,
• Evento-reconstrucción: Se va monitoreando el
comportamiento
de
las
RPI
mientras
evolucionan de acuerdo a las transiciones que
se van habilitando y que el usuario va
disparando, mediante el cálculo del error Ek .
• Calculo del error: Si Ek 0 entonces no se ha
disparado ninguna falta, pero si llega a ocurrir
que Ek 0 entonces ha ocurrido una falta.
• Aislamiento de faltas: El sistema analiza y aisla
la falta mediante un algoritmo que clasifica a
que conjunto de faltas pertenece, tal que:
• Resultado: Se muestra el cálculo al usuario en
una interfaz GUI de MATLAB®. ti T PF ti T OF

15. 2.6 Identificación de la falta
Si el valor del error es diferente de cero, una falta existe.
El error provee de un marcador de la falta como un
número que identifica el tipo de falta disparada en el
sistema:
• Si el error es igual a el valor entonces i será una falta
permanente.
• Si es diferente al valor entonces i será una falta
operacional y la transición disparada puede ser
conocida usando la diferencia entre el marcado
actual y el marcado anterior para obtener las
transiciones disparadas:
T k
Mk M K 1
Ec. 4.7
i k
Ec. 4.8
La transición encontrada, corresponde a una falta
operacional.

16. 3. Resultados y discusión

17. 3. Resultados y discusión
3.1 Ejemplo real: Sistema doméstico de
abastecimiento de agua

18. 3. Resultados y discusión
3.1.1 Modelado del sistema
Variable de
Rango de
estado
tareas
Tarea_Tinaco
{Vacío, medio
Lugares
{P1,P2,P3}
lleno, lleno}
Tarea_Bomba
{Apagada,
{P4,P5}
encendida}
Tarea_Cisterna
{Vacía, Llena}
{P6,P7}

19. 3. Resultados y discusión
3.4 Resultados del algoritmo
La interfaz gráfica
del
analizador de la propiedad
de
diagnosticabilidad
importa la estructura de la
Red desde NETLAB®, el
algoritmo implementado en
MATLAB® diferencia los
lugares observables y no
observables así como las
transiciones manipulables y
no manipulables. La GUI de
MATLAB® analiza si la RPI
es diagnosticable según la
caracterización
de
la
propiedad
de
20
diagnosticabilidad

20. 3. Resultados y discusión
3.4 Resultados del algoritmo
En la imagen podemos ver
el EDAF implementado en
una GUI de MATLAB. Se
puede
ver
que
ha
detectado que la bomba se
encuentra en estado de
apagado, esto por que el
sistema ha solicitado la
tarea de ese recurso, si se
detecta este tipo de falla
entonces el sistema no
puede seguir funcionando
y por consecuencia es una
falla permanente.
21

21. 3. Resultados y discusión
3.4 Resultados del algoritmo
• Se efectúa el análisis de la diagnosticabilidad a
partir de la estructura de la red.
• El modelado de las fallas es muy flexible ya que
permite el análisis de los posibles estados de falla
que existan en el sistema.
• Permite saber con exactitud cuál es el recurso en el
que la falta esta ocurriendo al momento de
demandarlo.

22. 4. Conclusión

23. 4. Conclusión
4.1 Condiciones que determinan la
ocurrencia de una falta
• La estructura de una RPI determina características
que determinan la propiedad de diagnosticabilidad de
sistemas.
•La propuesta del algoritmo utilizando problemas de
programación lineal permiten el análisis y simulación
de los sistemas representados mediante RPI evitando
un que el problema sea de complejidad polinomial.
•Se demostró que este esquema sirve para determinar
la propiedad de diagnosticabilidad y en
consecuencia la detección de fallas para sistemas
complejos.
24

24. 5. Referencias

25. 5. Referencias
1.
SAMPATH, M., SENGUPTA, R., LAFORTUNE, S., SINNAMOHIDEEN, K. Y
TENEKETZIS, D., (1996) Failure Diagnosis Using Discrete-Event Models. IEEE
TRANSACTIONS ON CONTROL SYSTEM TECHNOLOGY. 4(2): 105-124.
2.
RUIZ-BELTRÁN E., RAMÍREZ-TREVIÑO, A., Y LÓPEZ-MELLADO E. (2004) Building
Diagnosable Petri Net Models for Distributed Fault Location of Discrete Event Systems.
IEEE INT. CONF. ON SYSTEMS, MAN, AND CYBERNETICS. :4929-4934
3.
RAMÍREZ-TREVIÑO, A., RUIZ-BELTRÁN, E., RIVERA-RANGEL, I., LÓPEZMELLADO, E., (2007) On-line Fault Diagnosis of Discrete Event Systems. A Petri Net
Based Approach, IEEE TRANSACTIONS ON AUTOMATION SCIENCE AND
ENGINEERING. 1(4): 557-565.
4. DOTOLI, M., PIA-FANTI, M., MANGINI , A. Y UKOVICH, W., 45(2009) On-line fault
detection in discrete event systems by Petri nets and integer linear programming.
AUTOMATICA. 1(45): 2665-2672.
5. HADJICOSTIS, C. N. Y Li, L., (2011) Least-Cost Transition Firing sequence estimation in
labelled Petri nets with unobservable transitions. IEEE TRANSACTION ON
AUTOMATON SCIENCE AND ENGINEERING. 8(2): 394- 403.
6. ARREDONDO-GARCÍA A., RUIZ-BELTRÁN E., Y OROZCO-MORA J. L. (2012)
Detección de fallas en línea. 13° Seminario de Investigación UAA.
26