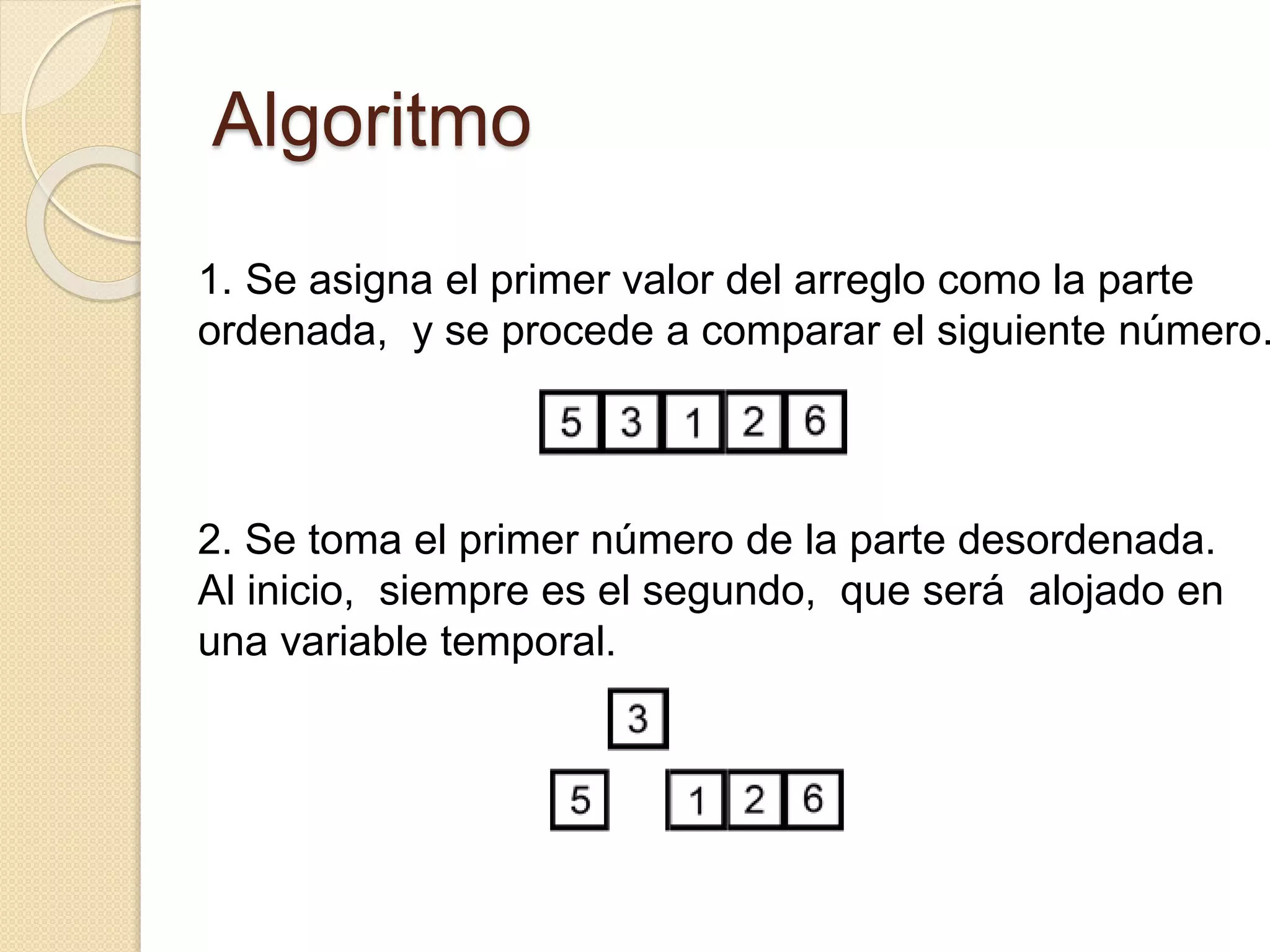
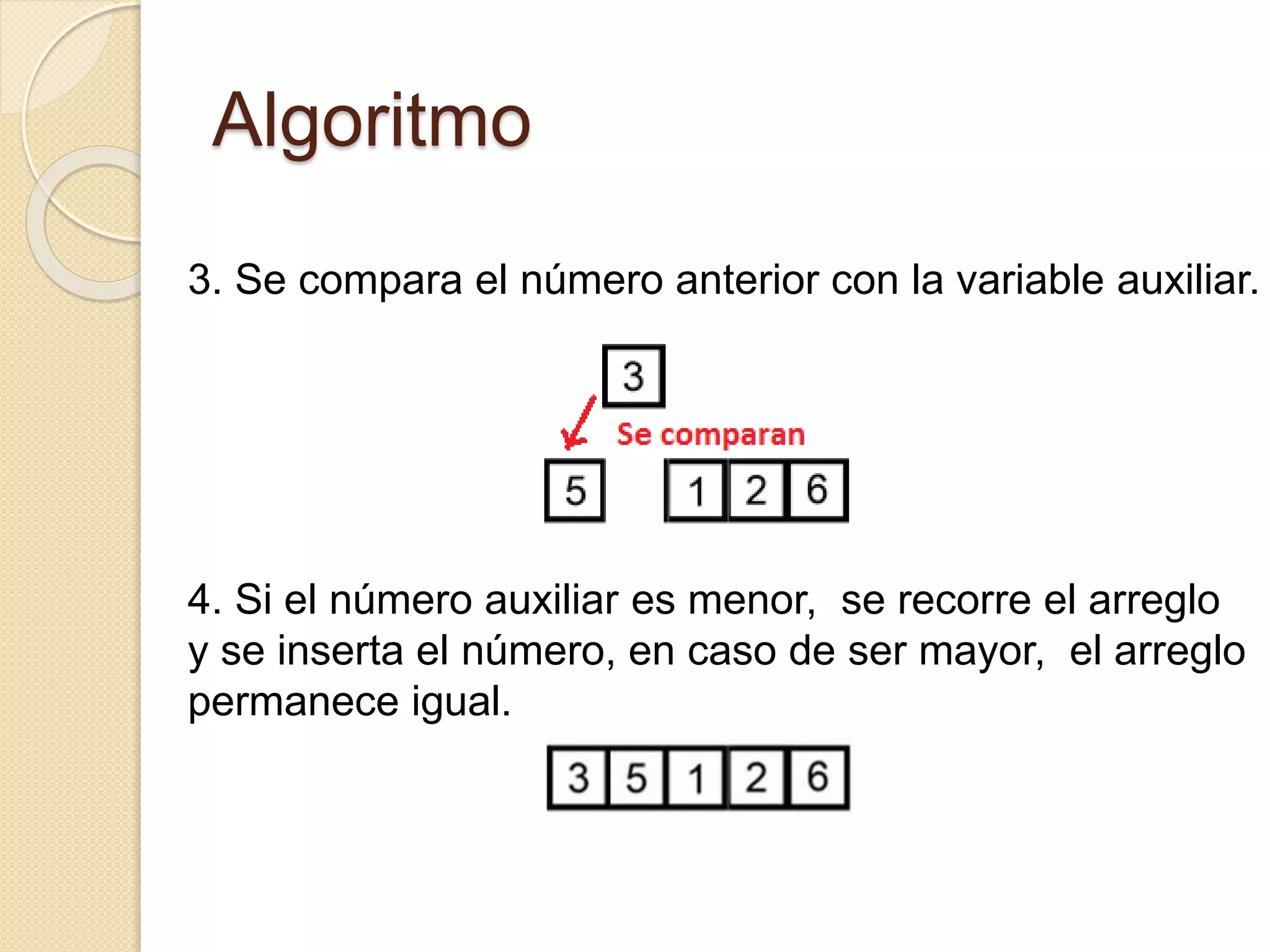
El documento describe el algoritmo de ordenación por inserción directa. El algoritmo ordena un arreglo insertando cada elemento en su posición correcta mediante comparaciones. En cada pasada, se analiza un elemento y se desplaza por la parte ordenada del arreglo hasta encontrar su lugar. Cuando todos los elementos han sido analizados, el arreglo está completamente ordenado. El algoritmo es estable y tiene una complejidad de O(n^2) en el peor caso y O(n) en el mejor caso.

1. Inserción Directa
Materia: Algoritmos y Estructuras de Datos
Maestro: Alma Leticia Palacios Jiménez
Integrantes del equipo:
• Bautista Mota Daniel
• Ruiz Esparza Terán Guillermo
• Mungarro Mora Gustavo Josué

2. Introducción
 Por la naturalidad del algoritmo, no se tiene un
origen en específico o más bien no se atribuye
su descubrimiento a alguien, puesto que desde
la existencia de las computadoras casi cualquier
persona que pudiera tener alcance a ellas, pudo
haber implementado el método de inserción
directa..
 Este algoritmo se basa en hacer comparaciones,
así que para que realice su trabajo de
ordenación son imprescindibles dos cosas: un
arreglo o estructura similar de elementos
comparables y un criterio claro de comparación,
tal que dados dos elementos nos diga si están
en orden o no.

3. Método de ordenación
El algoritmo consiste en realizar varias
pasadas sobre el arreglo. En cada pasada se
analiza un elemento, y se intenta encontrar
su orden relativo entre los analizados en
pasadas anteriores.
Con esto se logra ir manteniendo una lista
ordenada constantemente.
Cada elemento a analizar se desplaza por
esa lista hasta encontrar su lugar. Cuando
todos los elementos del arreglo han sido
analizados, la lista está completamente
ordenada.

4. Análisis del algoritmo
 Estabilidad: Este algoritmo nunca
intercambia registros con claves iguales. Por
lo tanto es estable.
 Requerimientos de Memoria: Una variable
adicional para realizar los intercambios.
 Tiempo de Ejecución: Para una lista de N
elementos el ciclo externo se ejecuta N
veces. El ciclo interno se ejecuta como
máximo una vez en la primera iteración, 2
veces en la segunda, 3 veces en la tercera,
etc.

5. Algoritmo
1. Se asigna el primer valor del arreglo como la parte
ordenada, y se procede a comparar el siguiente número.
2. Se toma el primer número de la parte desordenada.
Al inicio, siempre es el segundo, que será alojado en
una variable temporal.

6. Algoritmo
3. Se compara el número anterior con la variable auxiliar.
4. Si el número auxiliar es menor, se recorre el arreglo
y se inserta el número, en caso de ser mayor, el arreglo
permanece igual.

7. Pseudocódigo
Algoritmo Insercion(numeros, array_size)
Entradas: vector de n enteros
array_size tamaño del vector
Inicio
Declarar i, a, aux: enteros
for i =1 to i < array_size do{
aux ← numbers[i];
a ← i-1;
while a >= 0 && numeros[a] > aux do{
numeros[a + 1] ← numeros[a];
a--;
}
numeros[a+1] ← aux;
}
}

8. Código
void Insercion(int numeros [], int array_size){
int i, a, aux;
for (i =1; i < array_size; i++){
aux = numbers[i];
a = i-1;
while (a >= 0 && numeros[a] > aux){
numeros[a + 1] = numeros[a];
a--;
}
numeros[a+1] = aux;
}
}

9. Complejidad
 Este algoritmos es estable en su
ordenación interna.
 Tiene como complejidad el peor de los
casos de O(n^2) y en el mejor de los
casos O(n), esto se da en el caso de
que el arreglo esté ordenado.

10. Ventajas y Desventajas
 Ventajas:
◦ Fácil implementación.
◦ Requerimientos mínimos de memoria.
 Desventajas:
◦ Lento.
◦ Realiza numerosas comparaciones.

11. Referencias
 http://latecladeescape.com/t/Ordenaci
%C3%B3n+por+inserci%C3%B3n+dir
ecta+(InsertionSort)
 http://www.ecured.cu/index.php/Orden
amiento_por_Inserci%C3%B3n
 https://prezi.com/vtdnmg_ezv8y/orden
amiento-por-insercion-directa/
 di002.edv.uniovi.es/~paule/material/Or
denacionII.pdf (PDF)