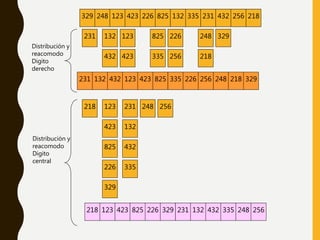
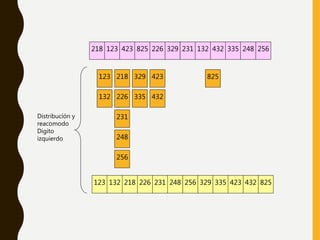
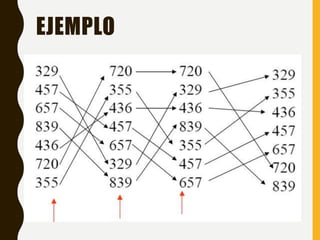
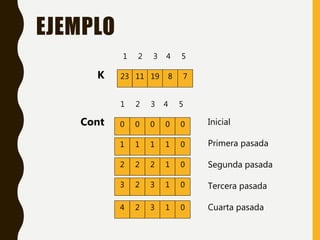
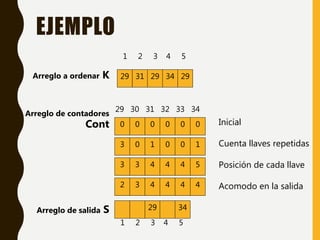
Este documento describe varios métodos de ordenamiento interno como inserción directa, burbuja, quicksort, shellsort, ordenamiento por conteo y ordenamiento por distribución. Explica los pasos de cada algoritmo y provee ejemplos para ilustrar cómo funcionan.

1. MÉTODOS DE
ORDENAMIENTO
INTERNOS

2. 6. ORDENACIÓN INTERNA
Algoritmos de ordenamiento por intercambio
 Burbuja
 Quicksort
 Shellsort
Algoritmos de ordenamiento por distribución
 Radix

3. INSERCIÓN DIRECTA
• Este método consiste en buscar el lugar adecuado para cada registro
recorriendo los registros anteriores para dejar un lugar vacío para el
nuevo elemento. El proceso de acomodo de cada elemento se repite
hasta llegar al último elemento, los elementos previos al elemento a
acomodar se encuentran en orden.
• Este es el método usado por los jugadores de cartas para acomodar su
juego.

4. ORDENAMIENTO POR INSERCIÓN
DIRECTA
Variables
– K arreglo de datos a ordenar
– V variable auxiliar
– i, j índices para el arreglo
– N número de elementos
InserciónDirecta
Inicio
Para i=2 hasta N incremento 1
v = K(i) //elemento a acomodar
j = i
Mientras (j > 1) y (K(j-1) > v)
K(j) = K(j-1) //mueve elementos
j = j-1
K(j) = v // inserta el elemento actual
Fin
3 8 2 1 4
1 2 3 4 5 6
2K
3 8
2 3 8
1 2 3 8
1 2 3 4 8
1 2 2 3 4 8

5. BURBUJA (BUBBLE)
• Este método realiza comparaciones de todas las posibles parejas de
llaves intercambiando aquellas que se encuentran fuera de orden.
• Utiliza un proceso repetitivo comparando las parejas de datos
adyacentes del inicio al final del arreglo donde, después de la primer
pasada la llave mayor queda en la última posición del arreglo.

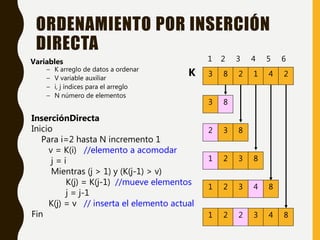
6. BURBUJA (BUBBLE)
Variables
• n es el total de elementos
• K arreglo de llaves
• t variable auxiliar para el intercambio
• i,j variables para los indices
Burbuja
Inicio
para i= n-1 ; i>0 ; i--
para j=0; i>j; j++
si (k[j] > k[j+1])
t = k[j];
k[j]= k[j+1];
k[j+1] = t;
Fin
3 8 2 1 4
0 1 2 3 4 5
2
3 8 2 1 4 2
3 2 8 1 4 2
3 2 1 8 4 2
3 2 1 4 8 2
3 2 1 4 2 8
Primera
pasada

7. 3 2 1 4 2 8
2 3 1 4 2 8
2 1 3 4 2 8
2 1 3 4 2 8
2 1 3 2 4 8
Segunda
pasada
2 1 3 2 4 8
1 2 3 2 4 8
1 2 3 2 4 8
1 2 2 3 4 8
Tercer
pasada
1 2 2 3 4 8
1 2 2 3 4 8
1 2 2 3 4 8
Cuarta
pasada
1 2 2 3 4 8
1 2 2 3 4 8
Quinta
pasada

8. SHELL SORT
• El método shell divide el arreglo a ordenar en varios grupos
haciendo comparaciones e intercambios entre ellos. El tamaño
de los subgrupos se decrementa y el número de subgrupos se
incrementa hasta llegar a tener n grupos de tamaño 1. A partir
de este punto, el método funciona como el de inserción directa.
• El tamaño de los subgrupos así como el total de estos puede
determinarlos el usuario para hacer mas eficiente el algoritmo.

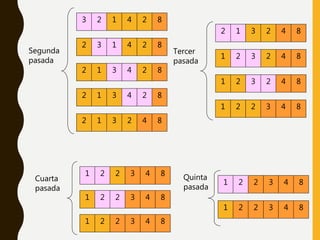
9. SHELL SORTVariables
– K arreglo de datos a ordenar
– H tamaño del grupo
– i, j índices para el arreglo
– V variable auxiliar
– N número de elementos
– grupo arreglo con los tamaños de grupo
Shellsort
Inicio
grupo = [ 21, 7, 3, 1]
para g=0; g<4; g++
h=grupo[g];
para i=h; i<n; i++
v=k[i];
j=i;
mientras (j>=h && a[j-h]>v)
k[j]=k[j-h];
j=j-h;
k[j]=v;
Fin
3 7 9 0 5 1 6 8 4 2 0 6 1 5 7 3 4 9 8 2
3 7 9 0 5 1 6 8 4 2 0 6 1 5 7 3 4 9 8 2
3 3 2 0 5 1 5 7 4 4 0 6 1 6 8 7 9 9 8 2
3 3 2 5 7 4 1 6 80 5 1 4 0 6 7 9 9 8 2
0 0 1 3 3 4 5 6 81 2 2 4 5 6 7 7 9 8 9
0 0 1 1 2 2 3 3 4 4 5 6 5 6 8 7 7 9 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9

10. RADIX
• Radix Sort (ordenamiento Radix) es un algoritmo de
ordenamiento estable* para ordenar elementos identificados
por llaves (o claves) únicas. Cada llave debe ser una cadena o
un número capaz de ser ordenada alfanuméricamente.
• Este método ejecuta un número de repeticiones igual al número
de caracteres de las llaves a ordenar. El Radix Directo, inicia
con el dígito más a la derecha repartiendo los datos en
“canastas”, estos datos se reparten de nuevo de acuerdo al
siguiente dígito y así sucesivamente hasta terminar con el dígito
de mas a la izquierda.

11. 329 248 123 423 226 825 132 335 231 432 256 218
Distribución y
reacomodo
Digito
derecho
329248123
423
226825132
335
231
432 256 218
231 132 432 123 423 825 335 226 256 248 218 329
231
132
432
123
423
825
335226
256248218
329
218 123 423 825 226 329 231 132 432 335 248 256
Distribución y
reacomodo
Digito
central

12. 231
132 432
123 423 825
335226
256
248
218 329
218 123 423 825 226 329 231 132 432 335 248 256
Distribución y
reacomodo
Digito
izquierdo
123 132 218 226 231 248 256 329 335 423 432 825

13. EJEMPLO

14. ALGORITMO:
QUICKSORT

15. DESCRIPCIÓN
• Se elige un pivote.
• Se reubican los elementos respecto al pivote los
menores antes, los mayores atrás.
• El arreglo queda separado en dos subarreglos
• Se repite el proceso con los subarreglos
resultantes
• El arreglo esta ordenado

16. DEMOSTRACIÓN
• Suponiendo que el número total de elementos a ordenar es
potencia de dos, es decir, n = 2k. De aquí podemos ver que k =
log2(n), donde k es el número de divisiones que realizará el
algoritmo.
• En la primera fase del algoritmo habrán n comparaciones, en la
segunda fase el algoritmo creará dos sublistas
aproximadamente de tamaño n/2. El número total de
comparaciones de estas dos sublistas es: 2(n/2) = n. En la
tercera fase el algoritmo procesará 4 sublistas más, por tanto el
número total de comparaciones en esta fase es 4(n/4) = n.
• En conclusión, el número total de comparaciones que hace el
algoritmo es:

17. TÉCNICAS DE ELECCIÓN DE PIVOTE
• El algoritmo básico del método Quicksort consiste en tomar
cualquier elemento de la lista al cual denominaremos como
pivote, dependiendo de la partición en que se elija, el algoritmo
será más o menos eficiente.
• Tomar un elemento cualquiera como pivote tiene la ventaja de
no requerir ningún cálculo adicional, lo cual lo hace bastante
rápido. Sin embargo, esta elección «a ciegas» siempre provoca
que el algoritmo tenga un orden de O(n²) para ciertas
permutaciones de los elementos en la lista.
• Otra opción puede ser recorrer la lista para saber de antemano
qué elemento ocupará la posición central de la lista, para
elegirlo como pivote.

18. ORDENAMIENTO POR
CONTEO
• Este método utiliza un arreglo auxiliar para contabilizar el
numero de llaves que son mayores que la llave actual.
• El arreglo de contadores, especifica la posición final donde
debería estar cada elemento.

19. ORDENAMIENTO POR
CONTEO
Variables
– K arreglo de datos a ordenar
– Cont arreglo de contadores
– N número de elementos a ordenar
ComparacionPorConteo
Inicio
inicializar el arreglo de contadores con cero en todas sus posiciones
Para i=N hasta 2 decremento 1
Para j=i-1 hasta 1 decremento 1
si K(i) < K(j) Cont(j)++
sino Cont(i)++
Fin

20. EJEMPLO
23 11 19 8 7
1 2 3 4 5
0 0 0 0 0
1 2 3 4 5
K
Cont
1 1 1 1 0
2 2 2 1 0
3 2 3 1 0
4 2 3 1 0
Inicial
Primera pasada
Segunda pasada
Tercera pasada
Cuarta pasada

21. ORDENAMIENTO POR
DISTRIBUCIÓN
• Este método es bueno aplicarlo cuando existen muchas claves
repetidas y estas se encuentran en un rango pequeño entre u y
v.
Rango u<=K1..n<=v
• Utiliza un arreglo contador con posiciones desde u hasta v,
además de un arreglo para generar la salida.

22. ORDENAMIENTO POR
DISTRIBUCIÓNVariables
– K arreglo de datos a ordenar
– Cont arreglo de contadores con índices desde u hasta v
– S arreglo de salida
– N número de elementos a ordenar
– U llave menor
– V llave mayor
Distribución
Inicio
inicializar el arreglo de contadores con cero en todas sus posiciones
Para i=1 hasta N incremento 1
Cont(K(i))++ // cuenta las llaves iguales
Para j=u+1 hasta v incremento 1
Cont(j) = Cont(j) + Cont(j-1) // localiza la posición de cada llave
Para j=N hasta 1 decremento 1
i = Cont(K(j))
S(i) = K(j) // envía la llave al vector de salida
Cont(K(j)) = Cont(K(j)) - 1
Fin

23. EJEMPLO
29 31 29 34 29
1 2 3 4 5
Arreglo a ordenar K
Arreglo de contadores
Cont
Arreglo de salida S 29 34
Inicial
Cuenta llaves repetidas
Posición de cada llave
Acomodo en la salida
0 0 0 0 0
29 30 31 32 33 34
3 0 1 0 0
3 3 4 4 4
0
1
5
2 3 4 4 4 4
1 2 3 4 5

24. EJERCICIOS PARA REALIZAR
• Ingresar 10 números aleatorios y ordenarlos por los siguientes
métodos
– Quicksort
– Shell
– Insercion