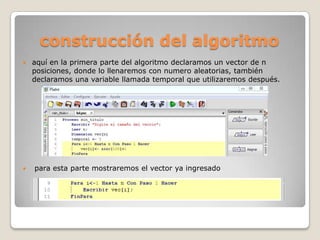
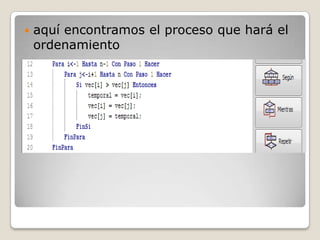
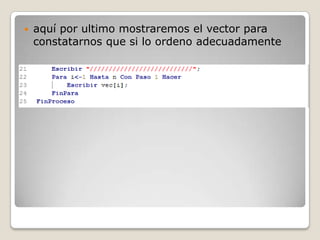
El algoritmo de ordenamiento por intercambio funciona comparando el primer elemento de un conjunto con los demás elementos y intercambiándolos si el primero es mayor. Este proceso se repite para el conjunto restante hasta que solo queda un elemento ordenado. Su complejidad es siempre O(n2) ya que la forma de operar es la misma independientemente de los datos. El documento explica la definición, construcción y proceso del algoritmo de ordenamiento por intercambio.

1. ORDENAMIENTO POR
INTERCAMBIO
Alvaro José Padilla
Wilmer Quintero

2. Definición
 El algoritmo del intercambio aunque es el más sencillo de
implementar es uno de los mas pobres en rendimiento, se basa
en la idea de buscar cada vez el menor elemento del conjunto y
ubicarlo al principio del mismo, repitiendo este proceso cada vez
con el conjunto sin su primer elemento (el menor del conjunto
anterior), hasta llegar a un conjunto de un solo elemento que por
definición ya está ordenado.
 En cada paso del algoritmo se compara el primer elemento del
conjunto x[i], con los demás elementos del mismo x[j] (j=i+1 ..
n) y cuando x[i] es mayor que x[j], se intercambian sus valores.
Cuando se termina de recorrer el arreglo el proceso nos garantiza
que en x[i] está el menor elemento del conjunto.
 Teniendo en cuenta que el algoritmo de ordenamiento por
intercambio se realiza siempre de la misma manera
independiente de los datos que estén almacenados, no existe un
mejor, peor o caso promedio y su complejidad siempre será O(n2)

4. Construcción en PSEINT

5. construcción del algoritmo
 aquí en la primera parte del algoritmo declaramos un vector de n
posiciones, donde lo llenaremos con numero aleatorias, también
declaramos una variable llamada temporal que utilizaremos después.
 para esta parte mostraremos el vector ya ingresado

6.  aquí encontramos el proceso que hará el
ordenamiento

7.  aquí por ultimo mostraremos el vector para
constatarnos que si lo ordeno adecuadamente

8. Muchas gracias