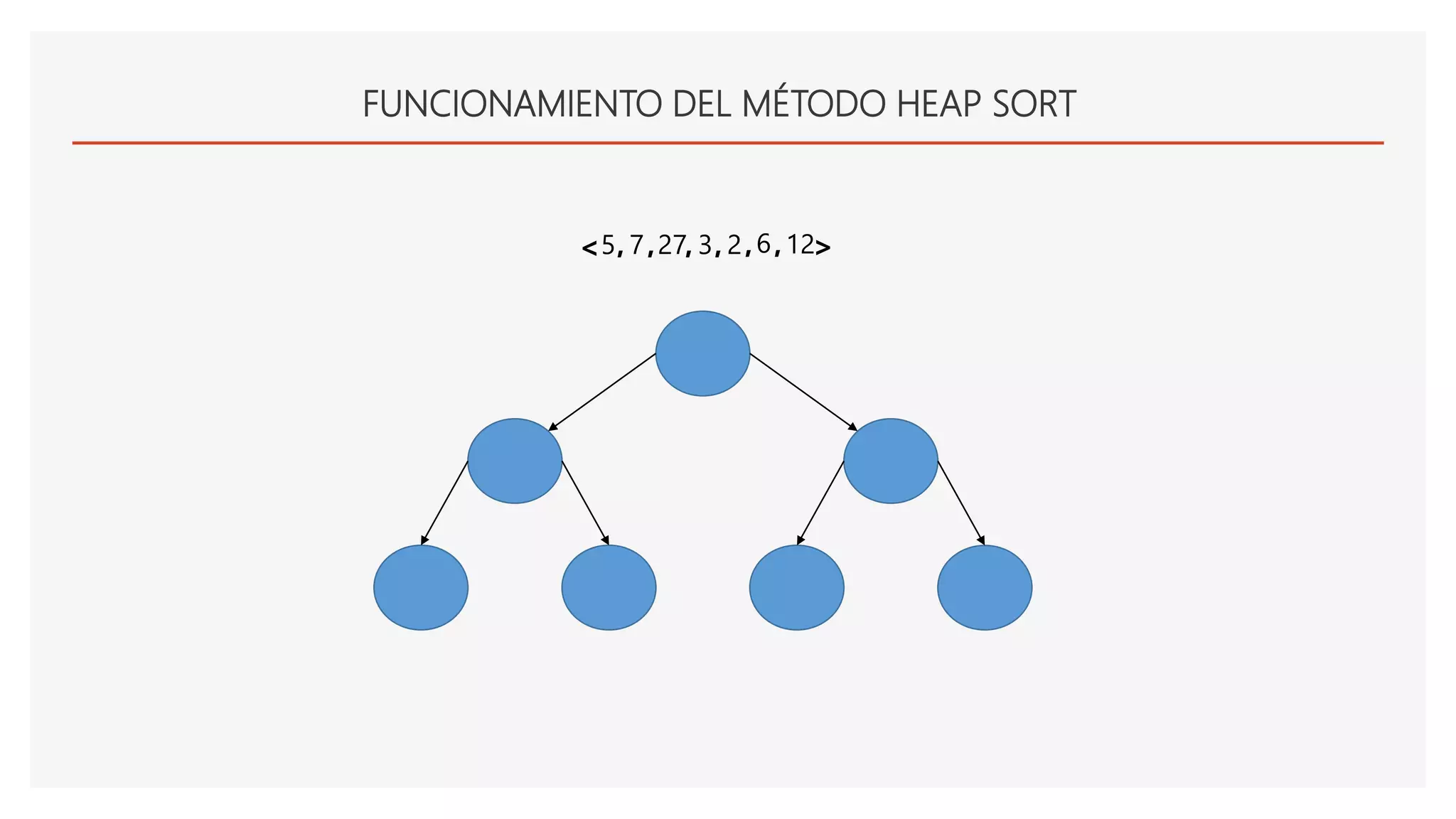
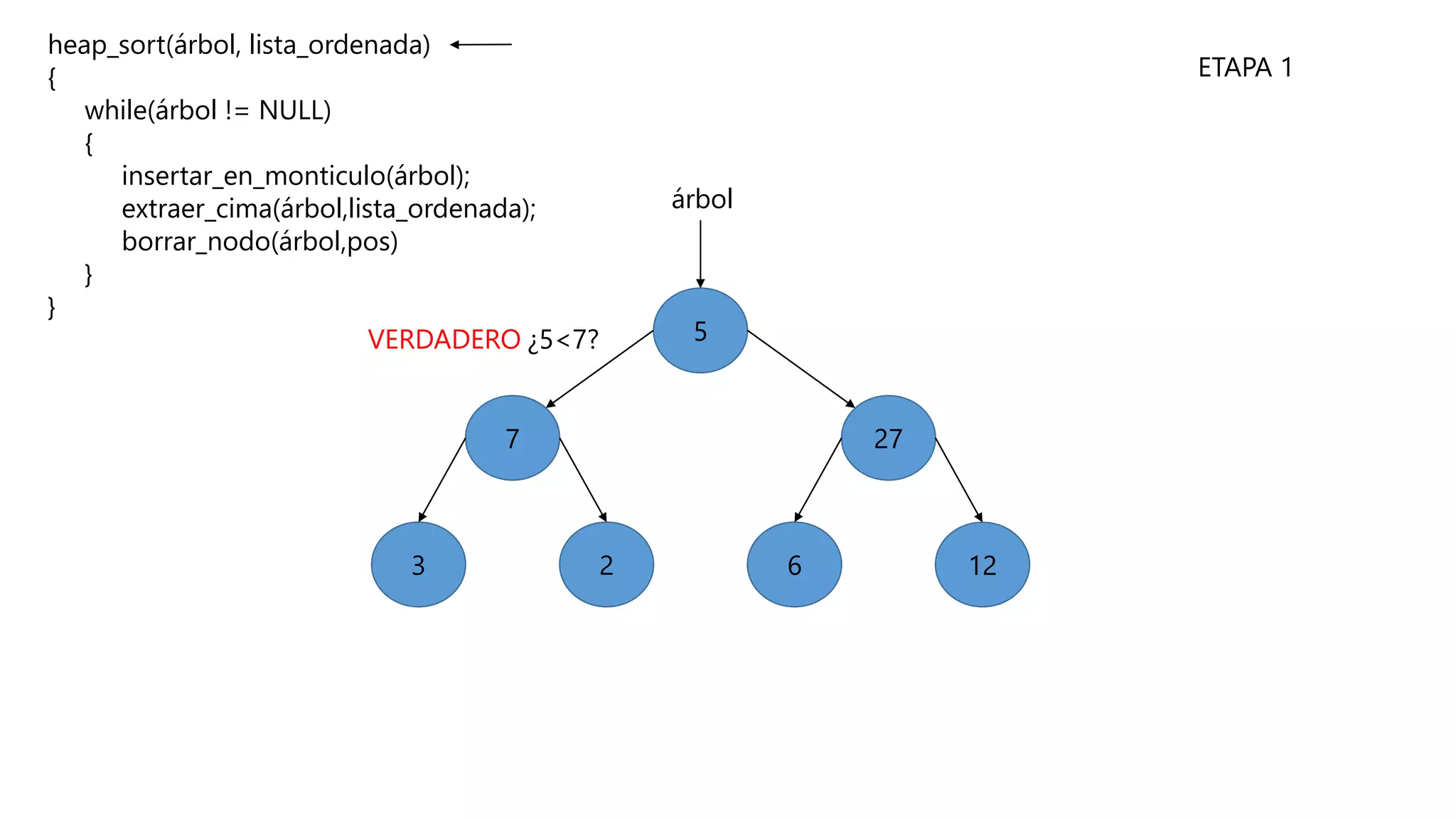
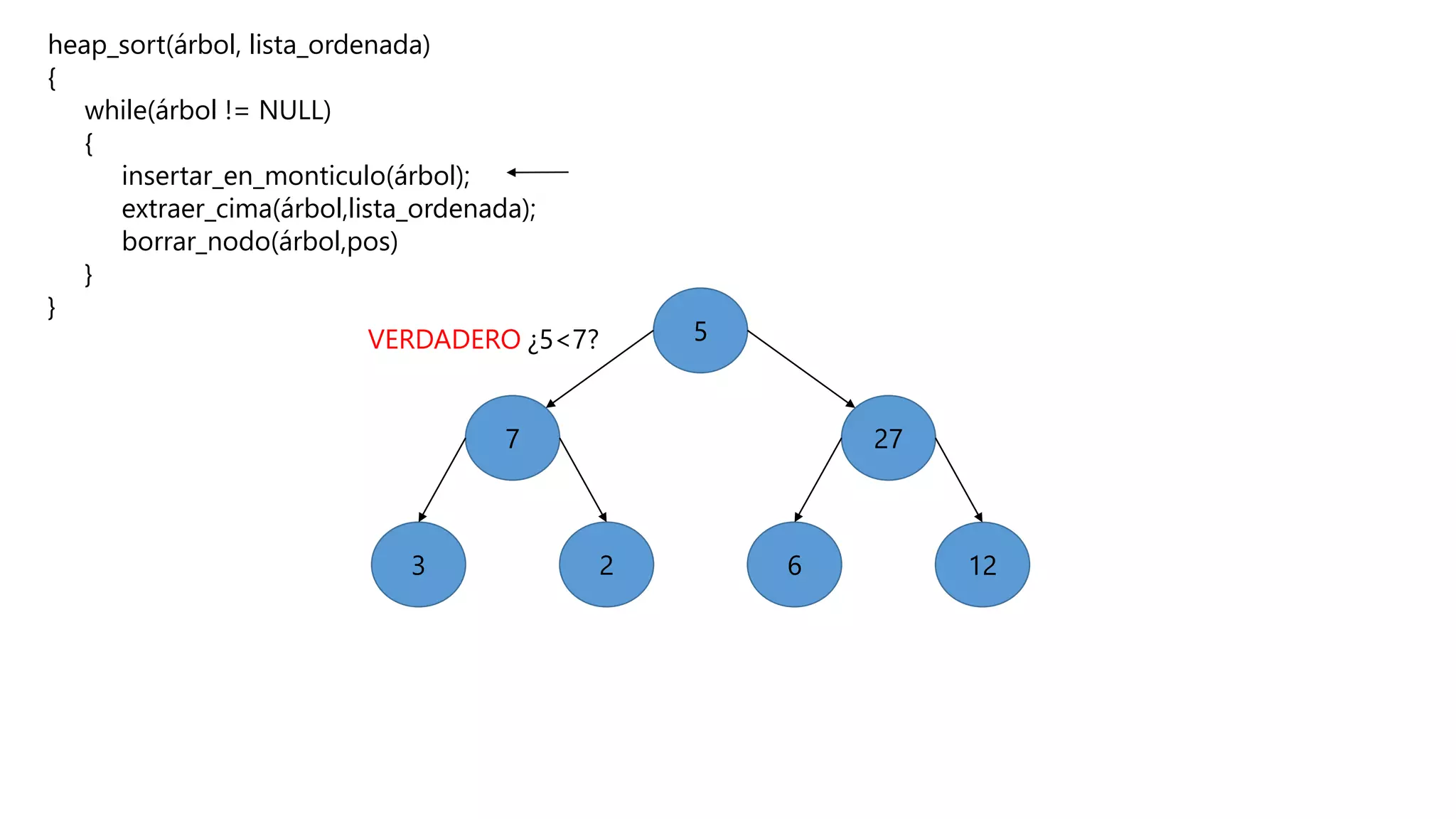
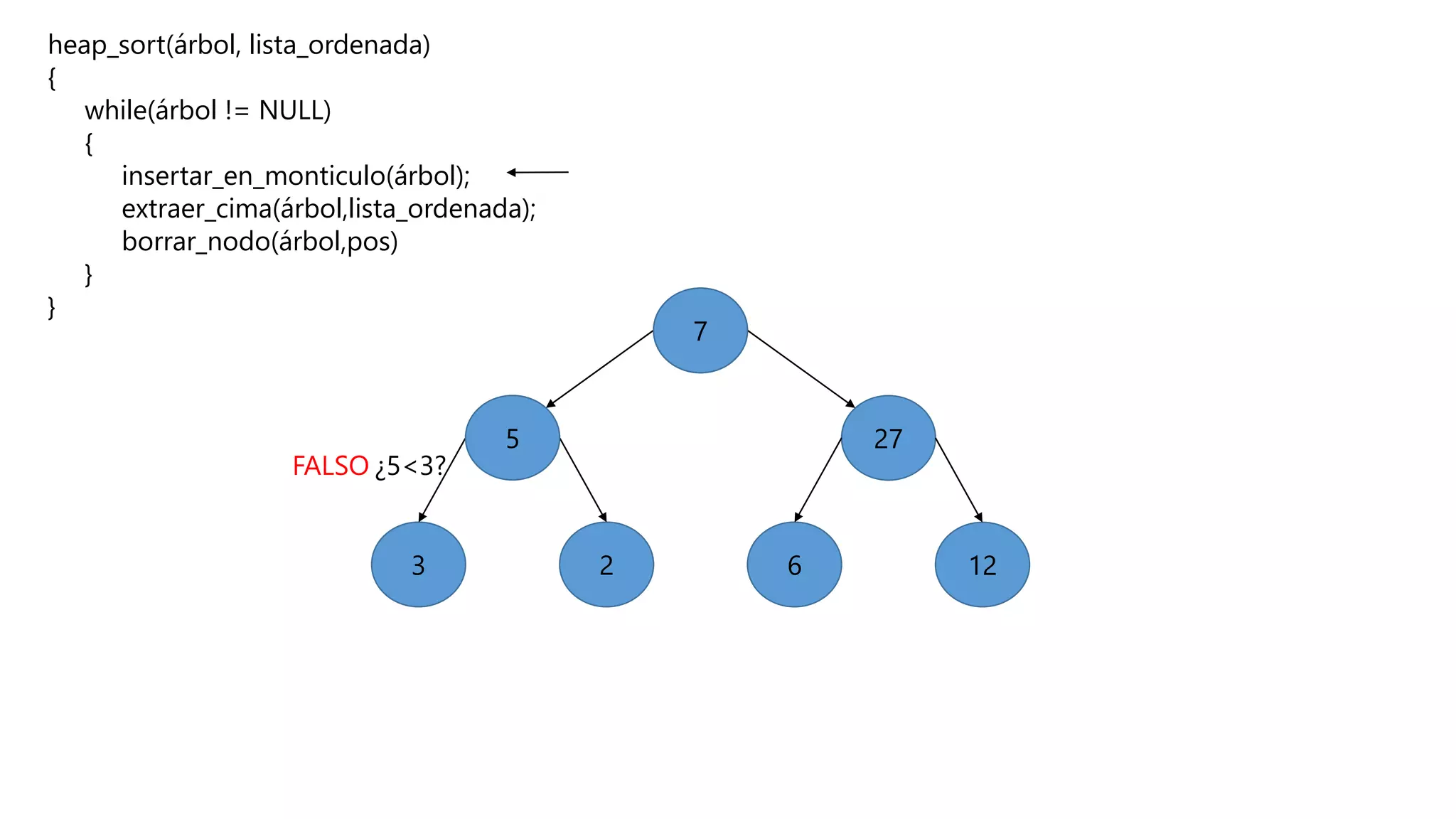
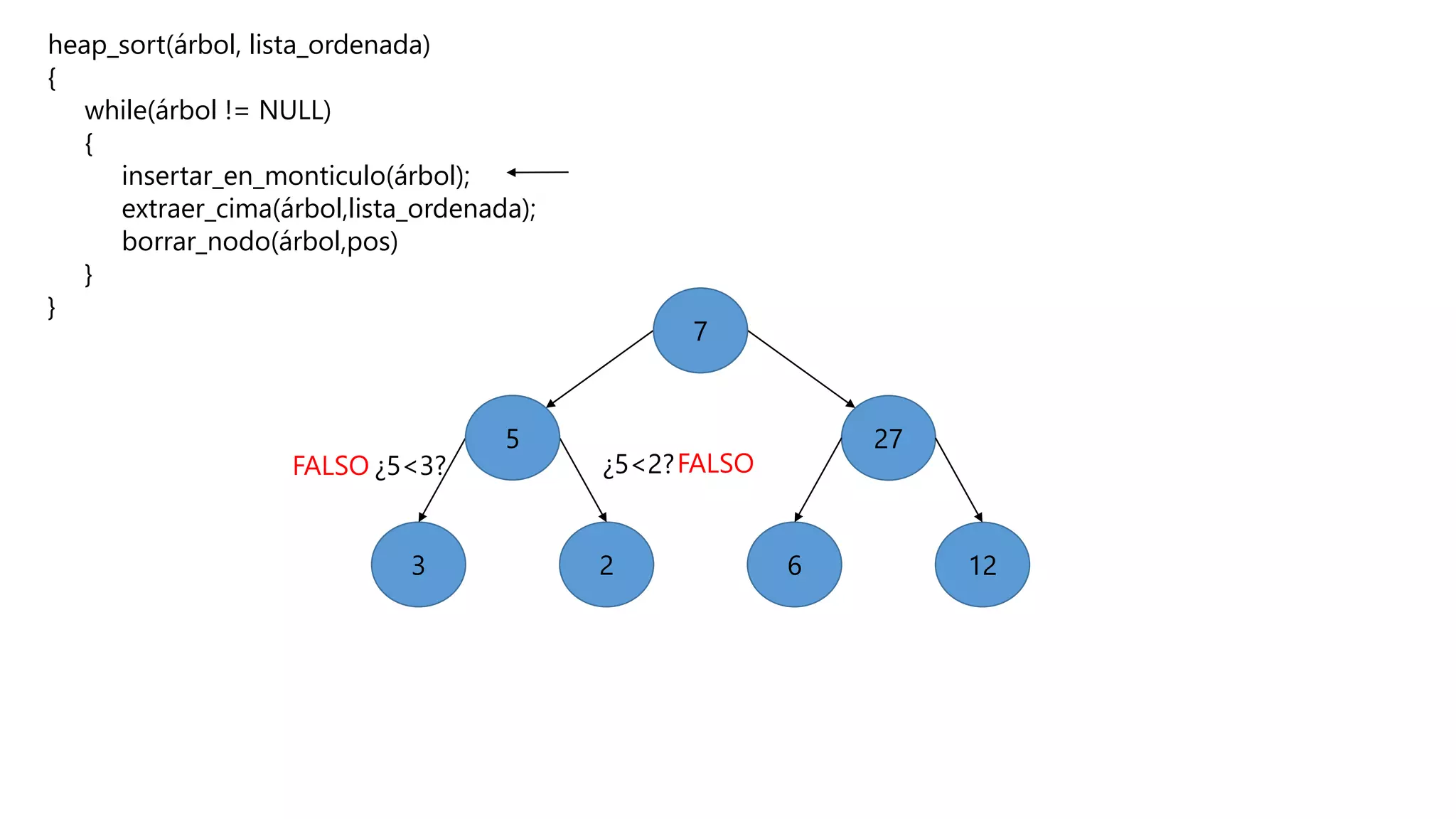
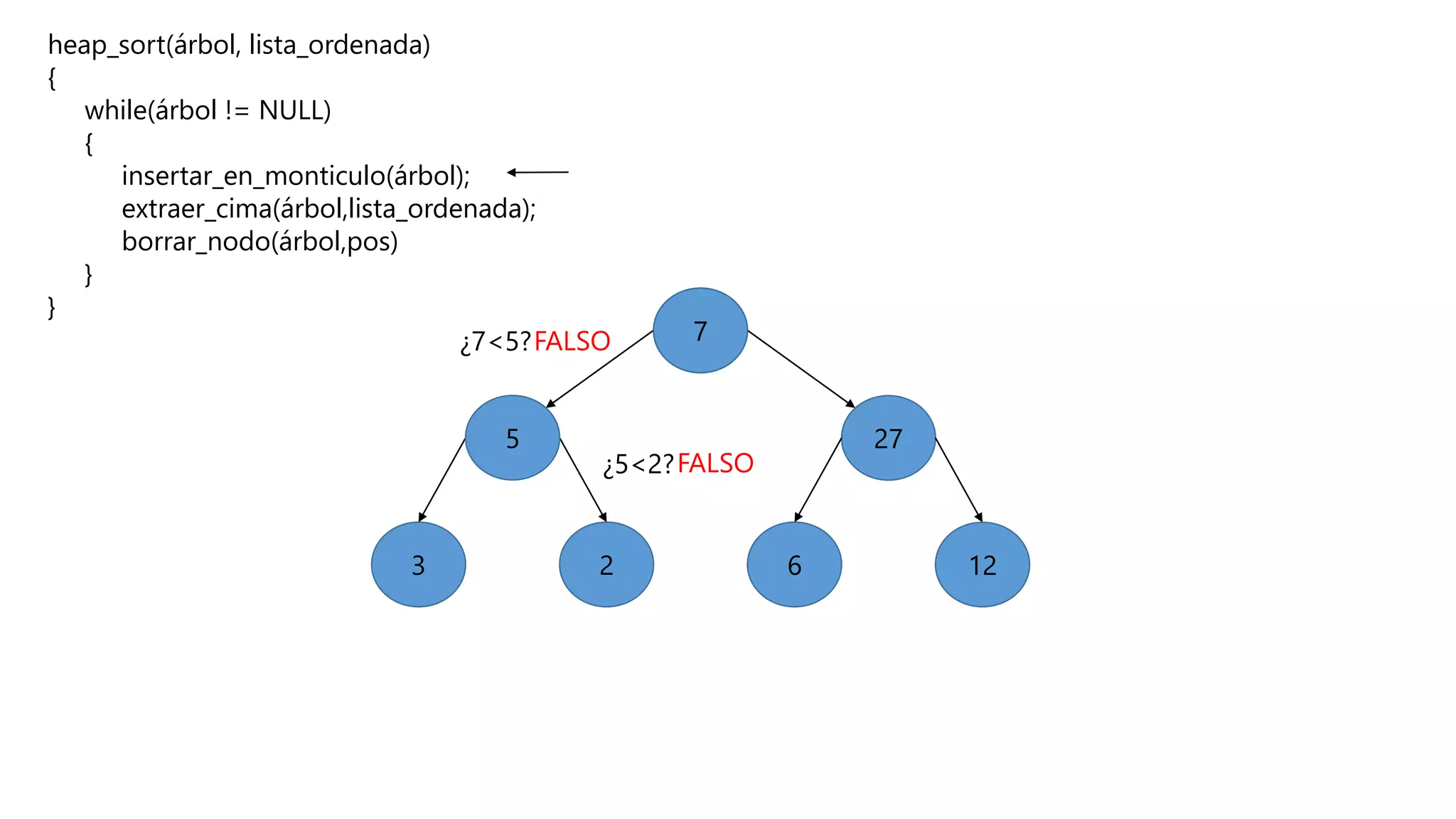
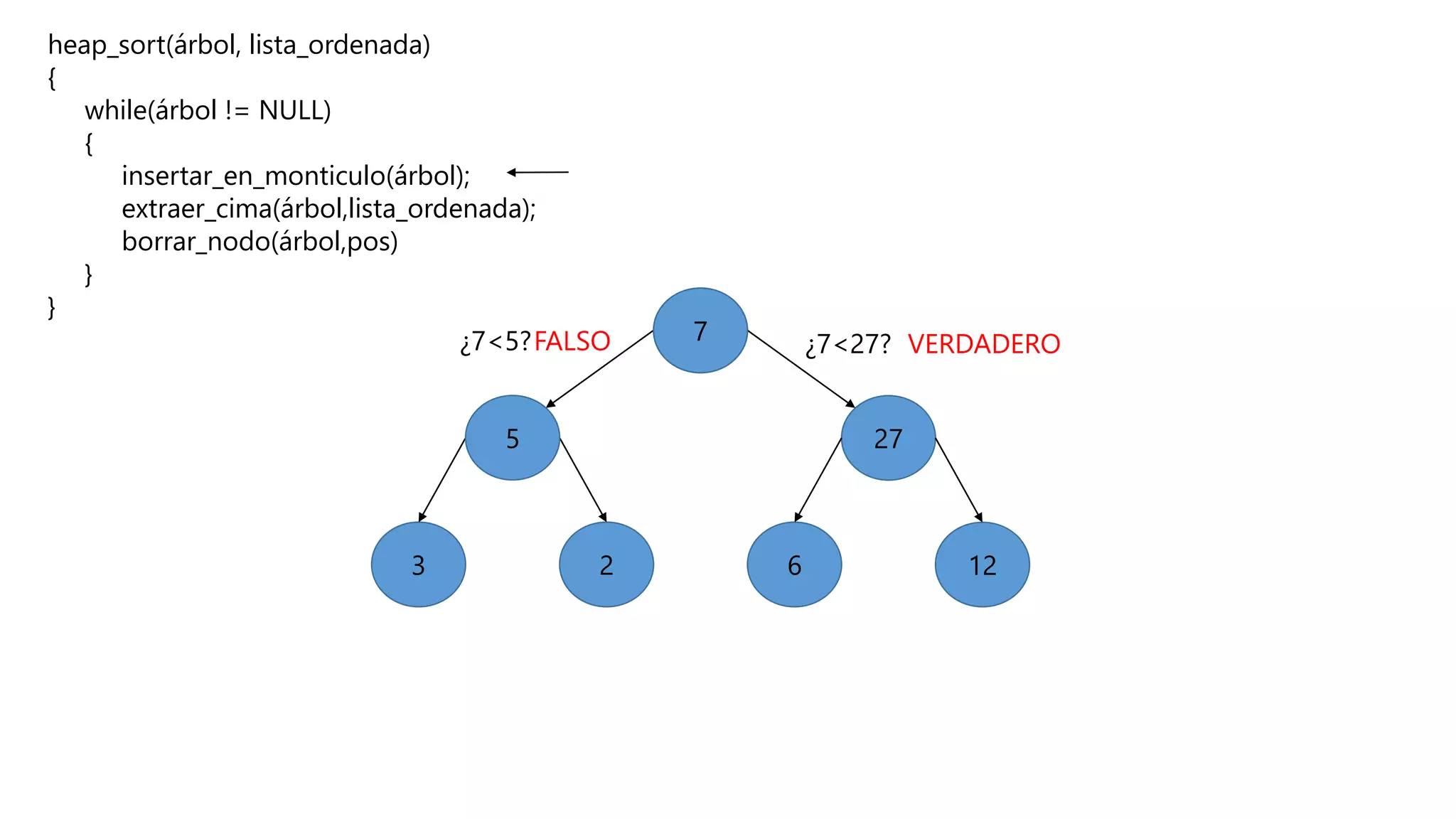
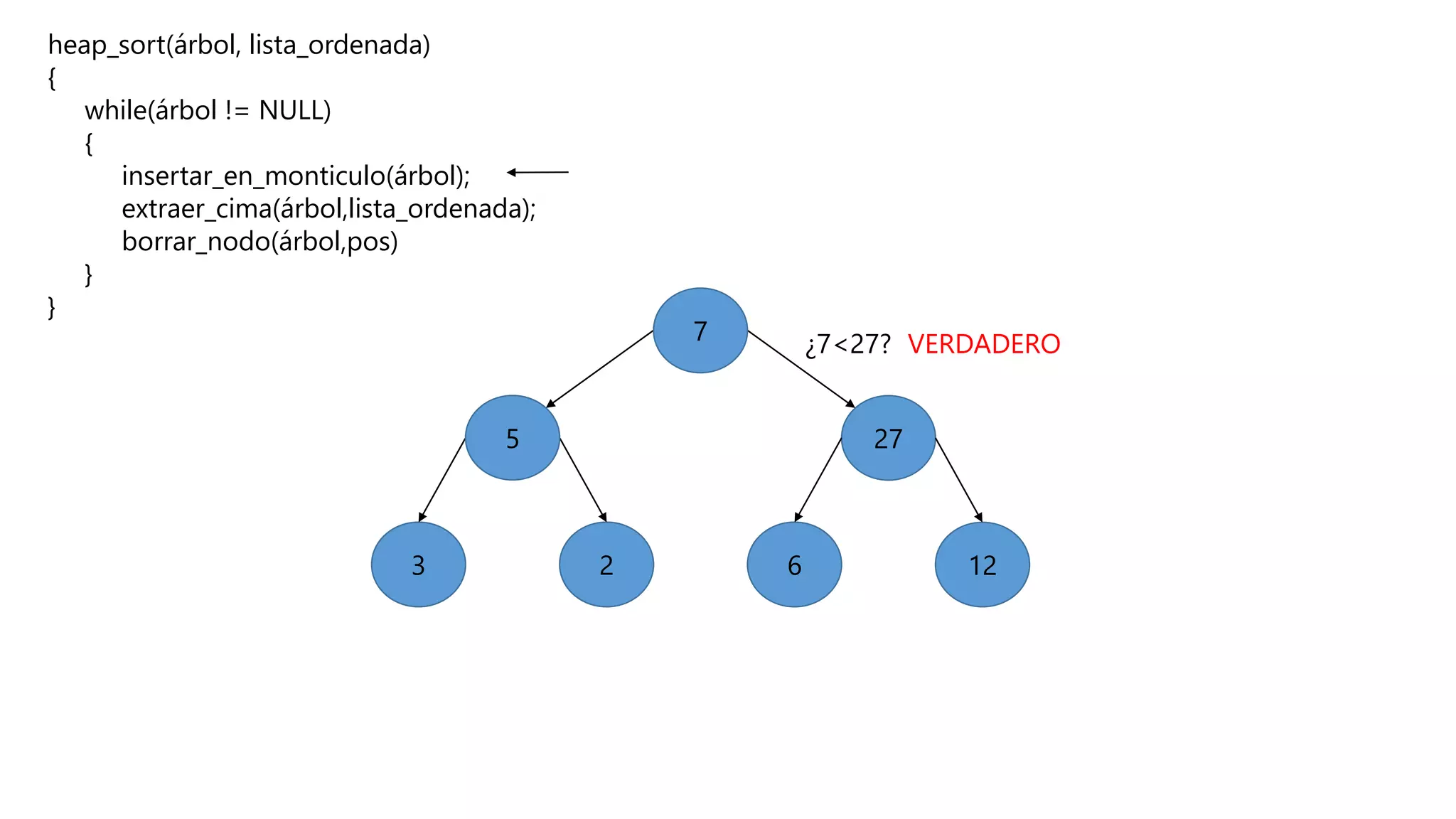
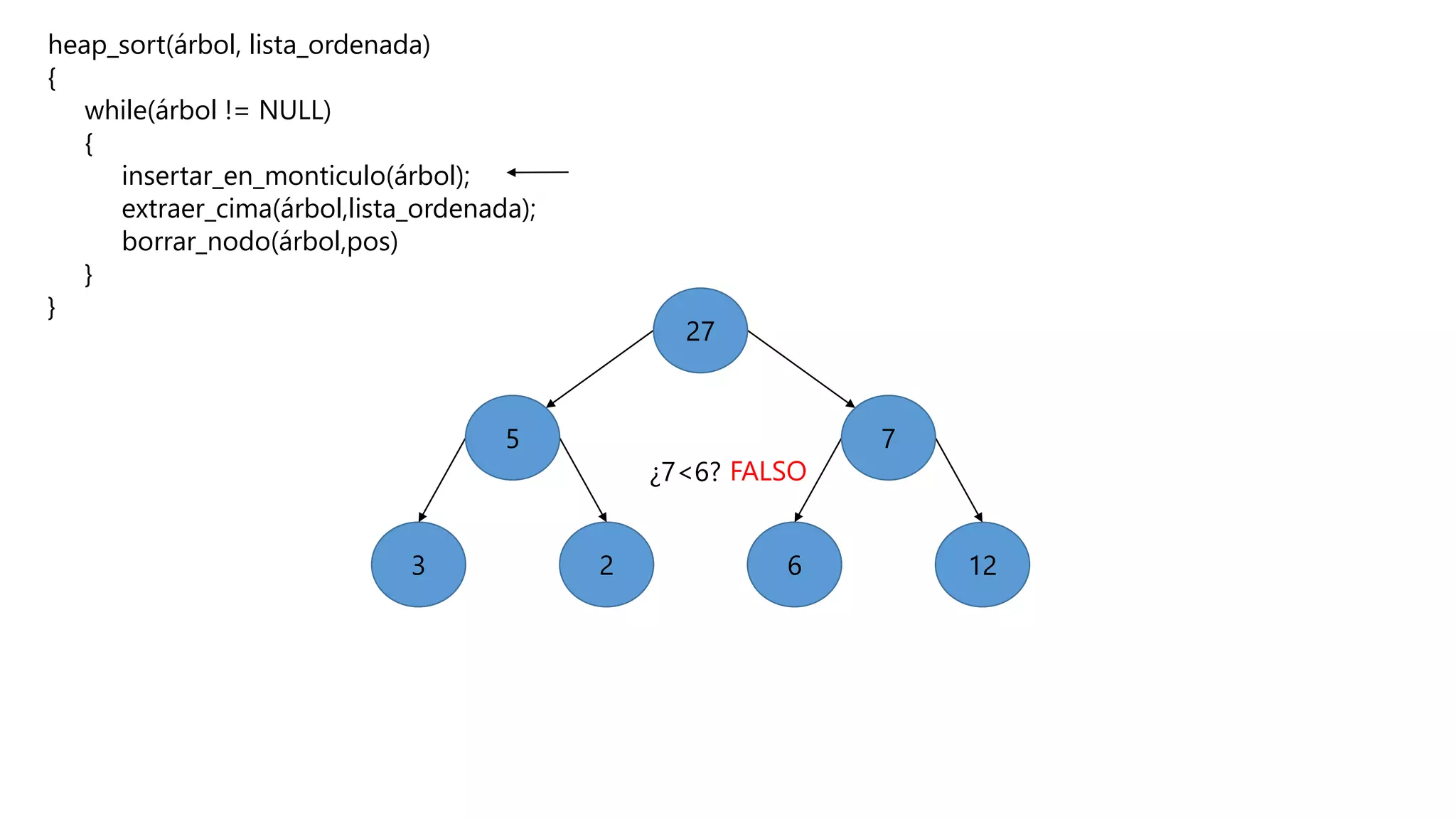
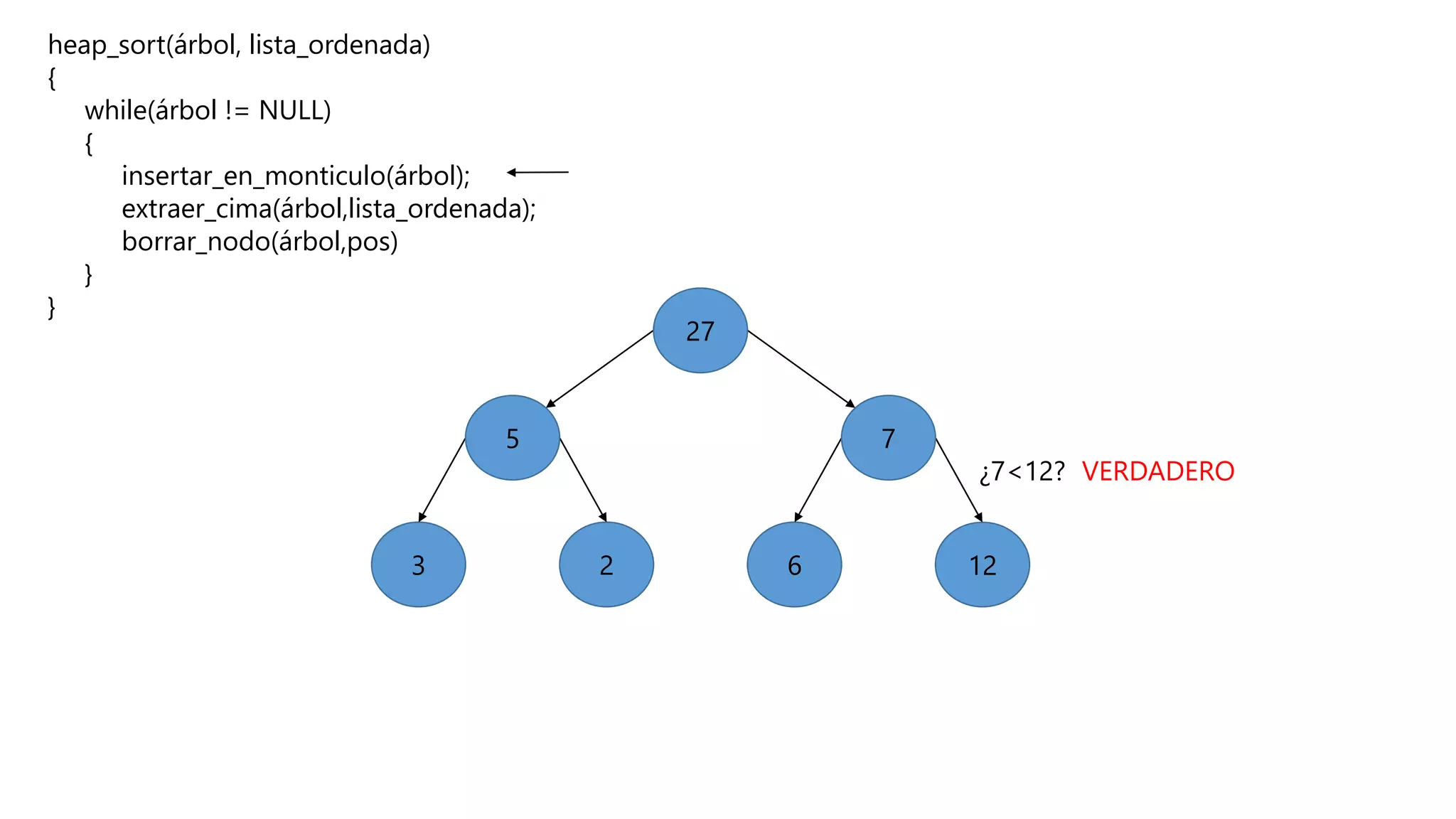
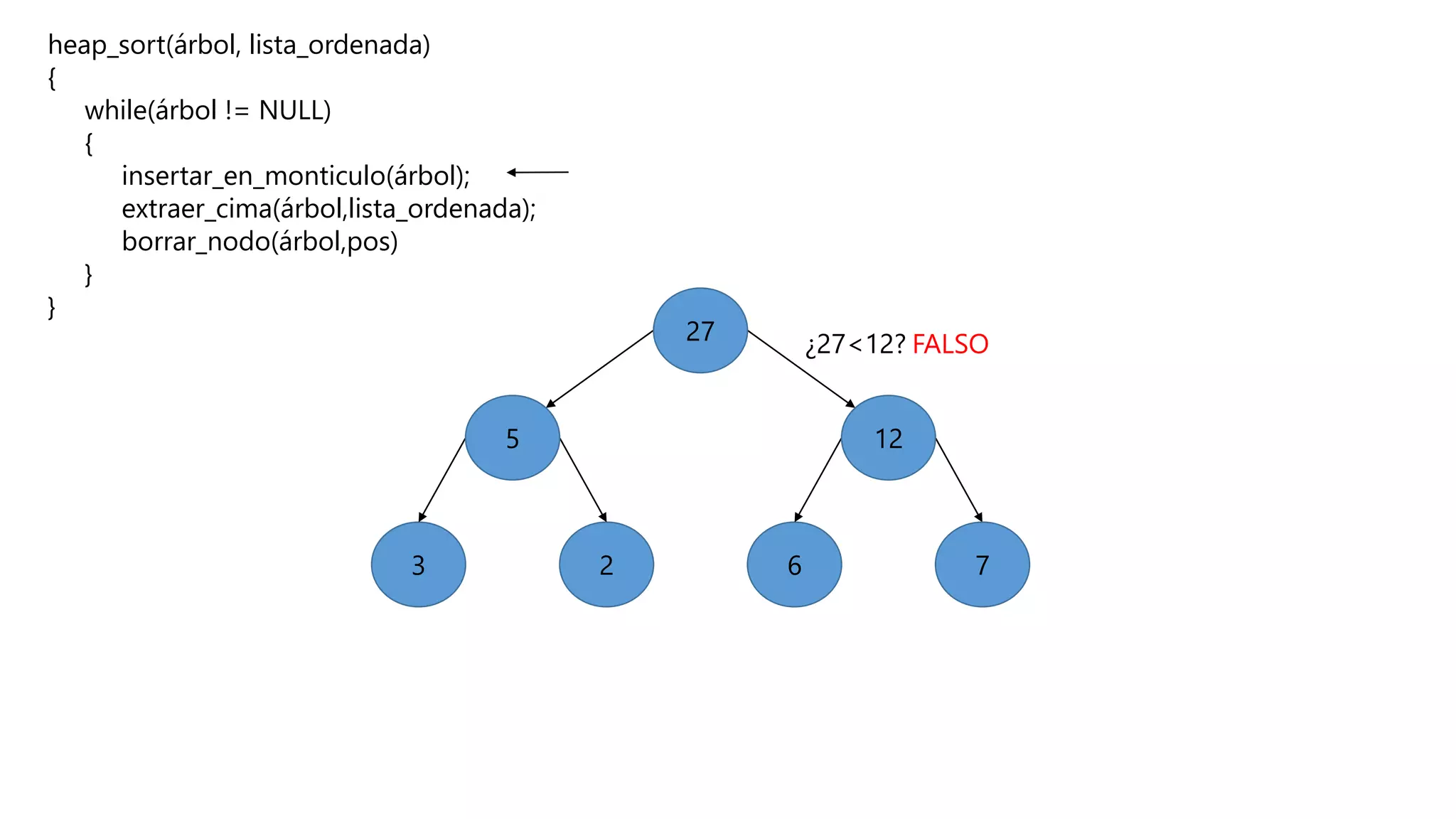
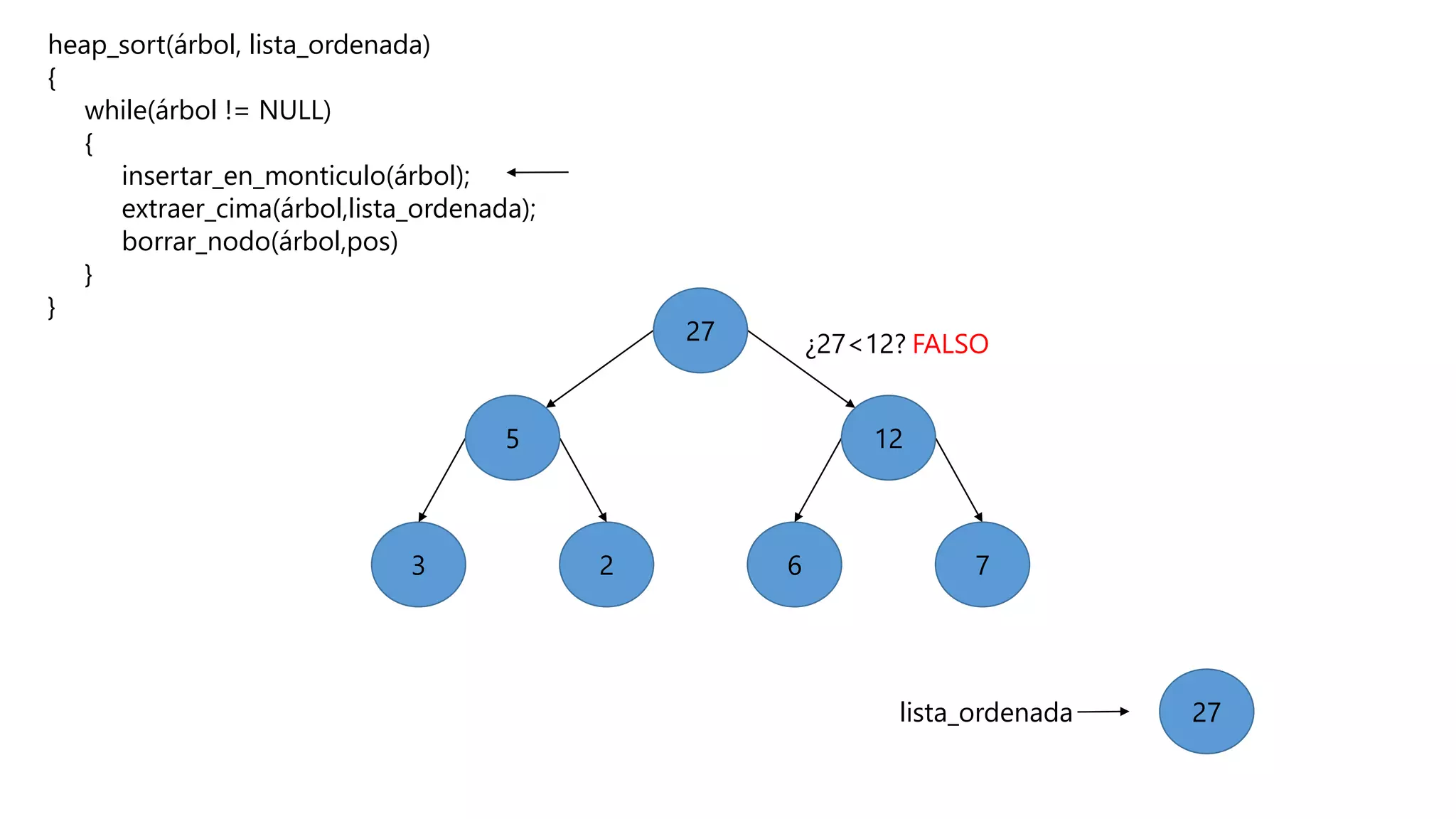
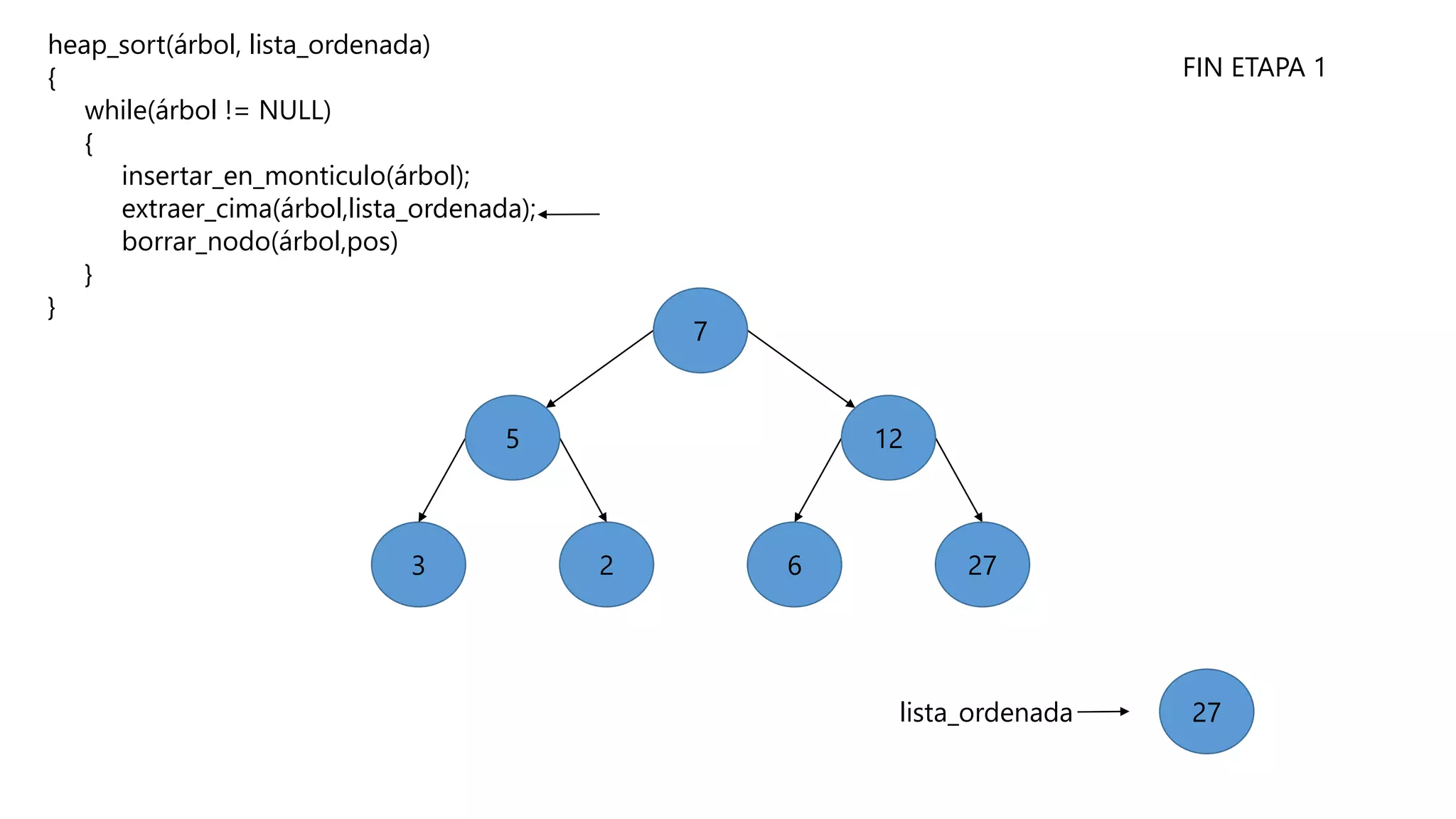
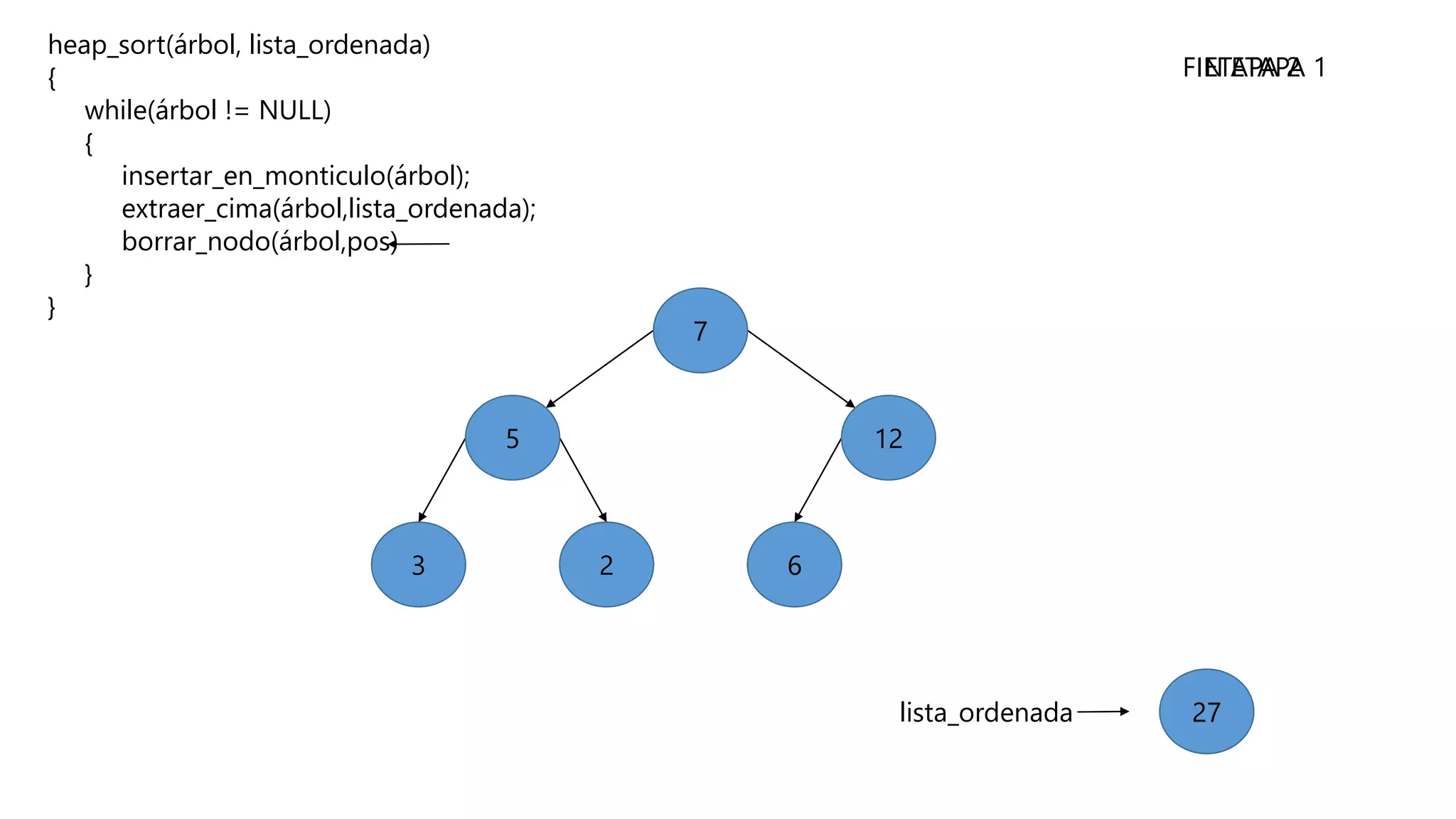
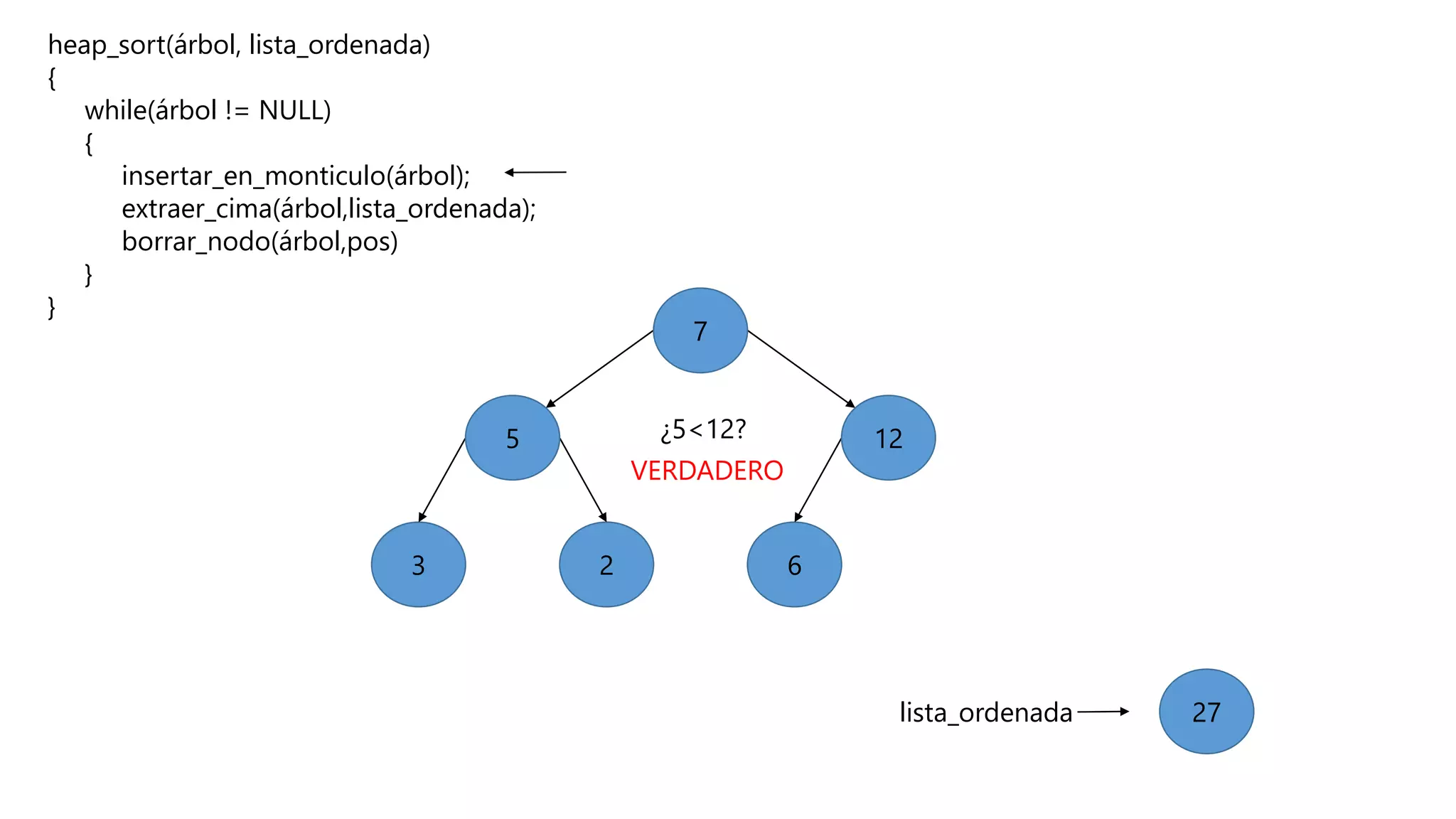
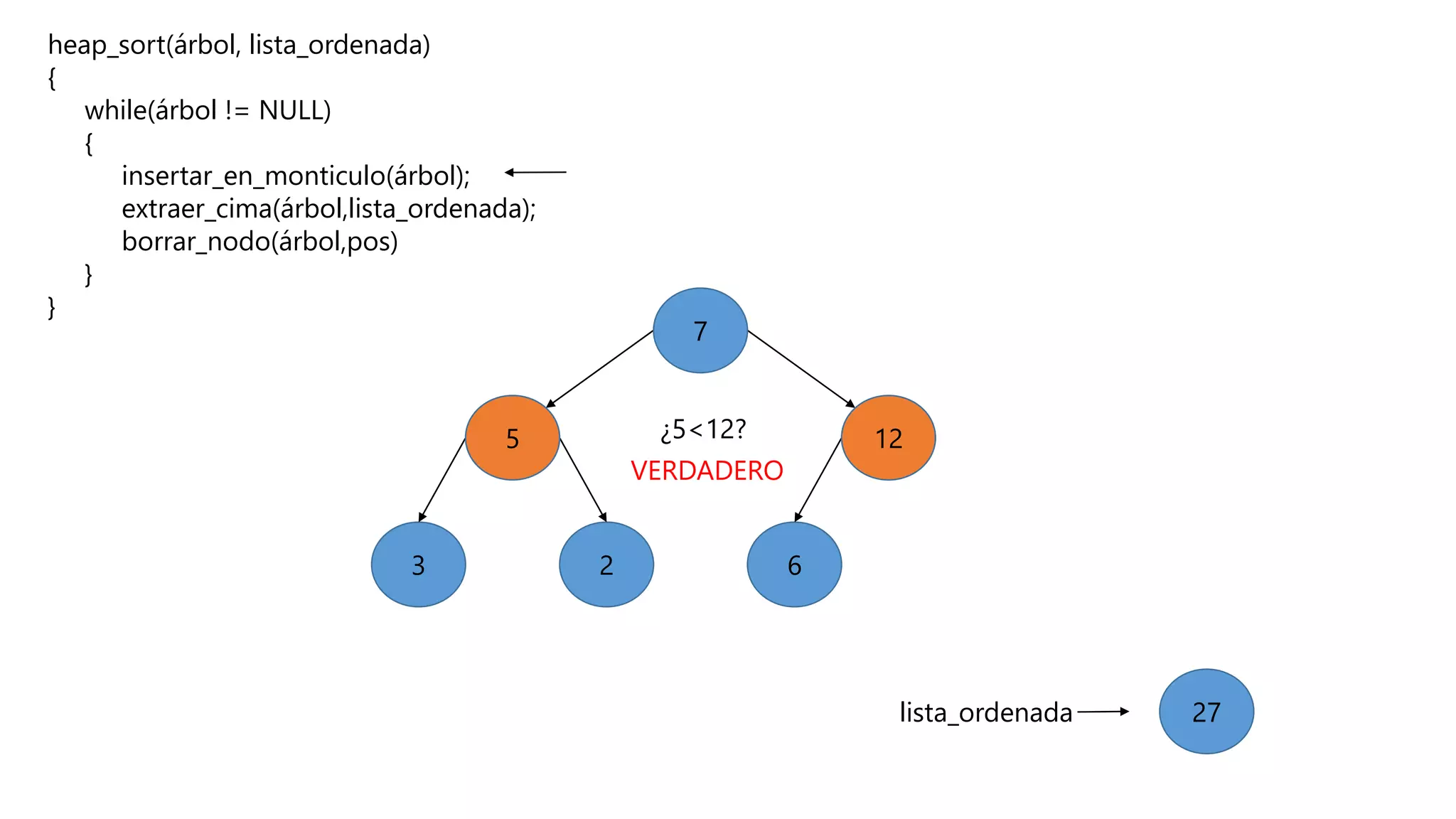
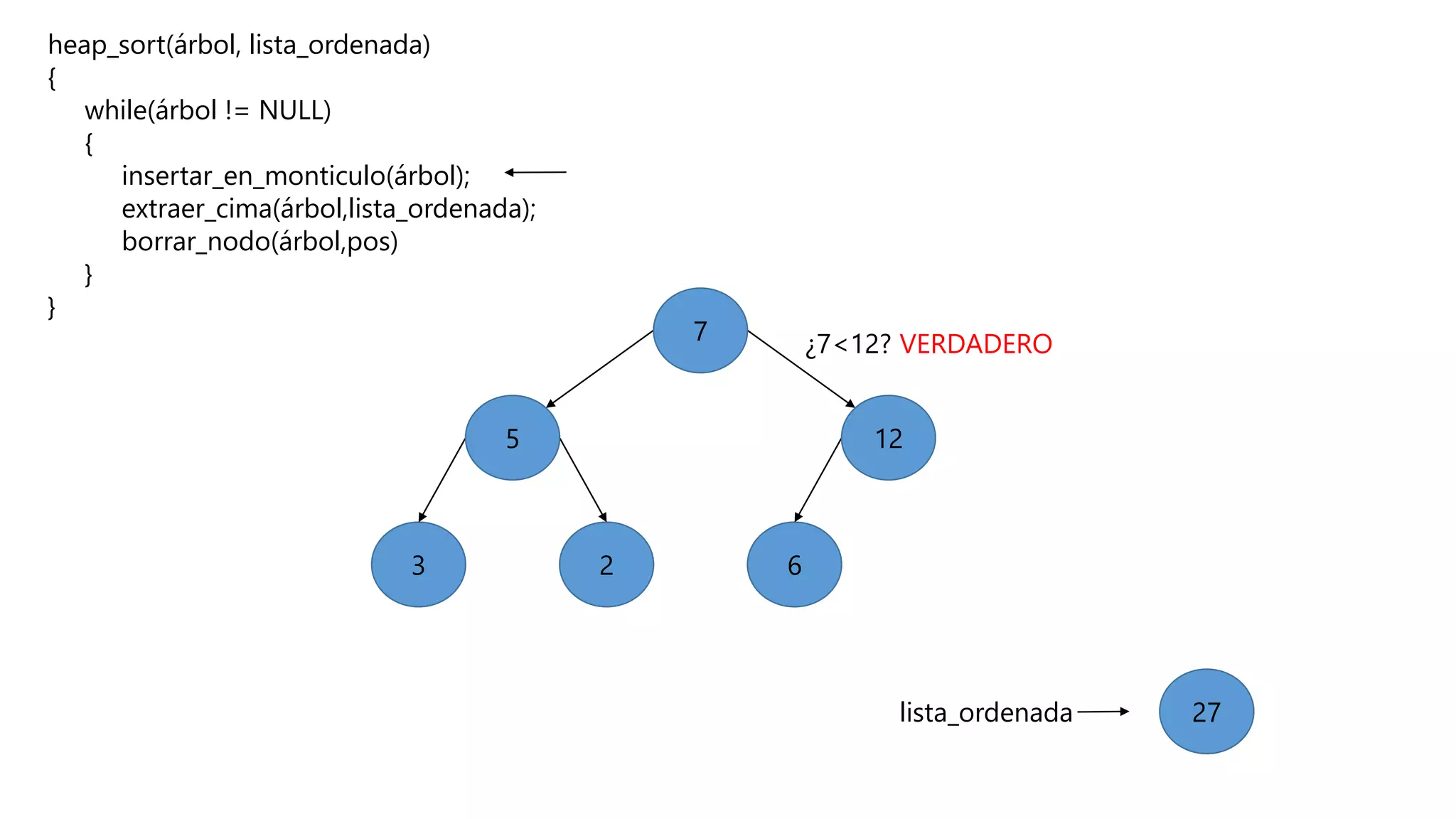
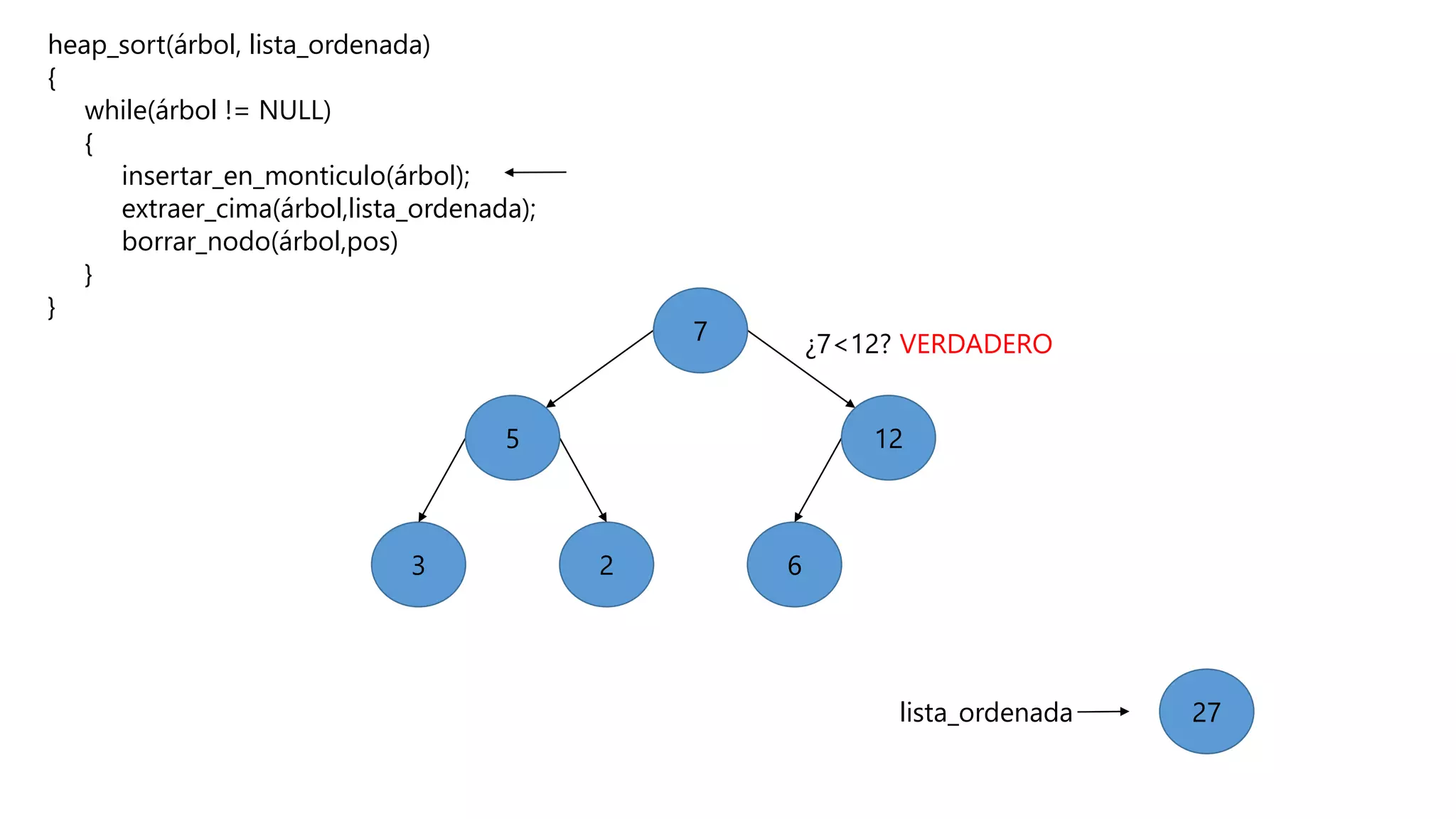
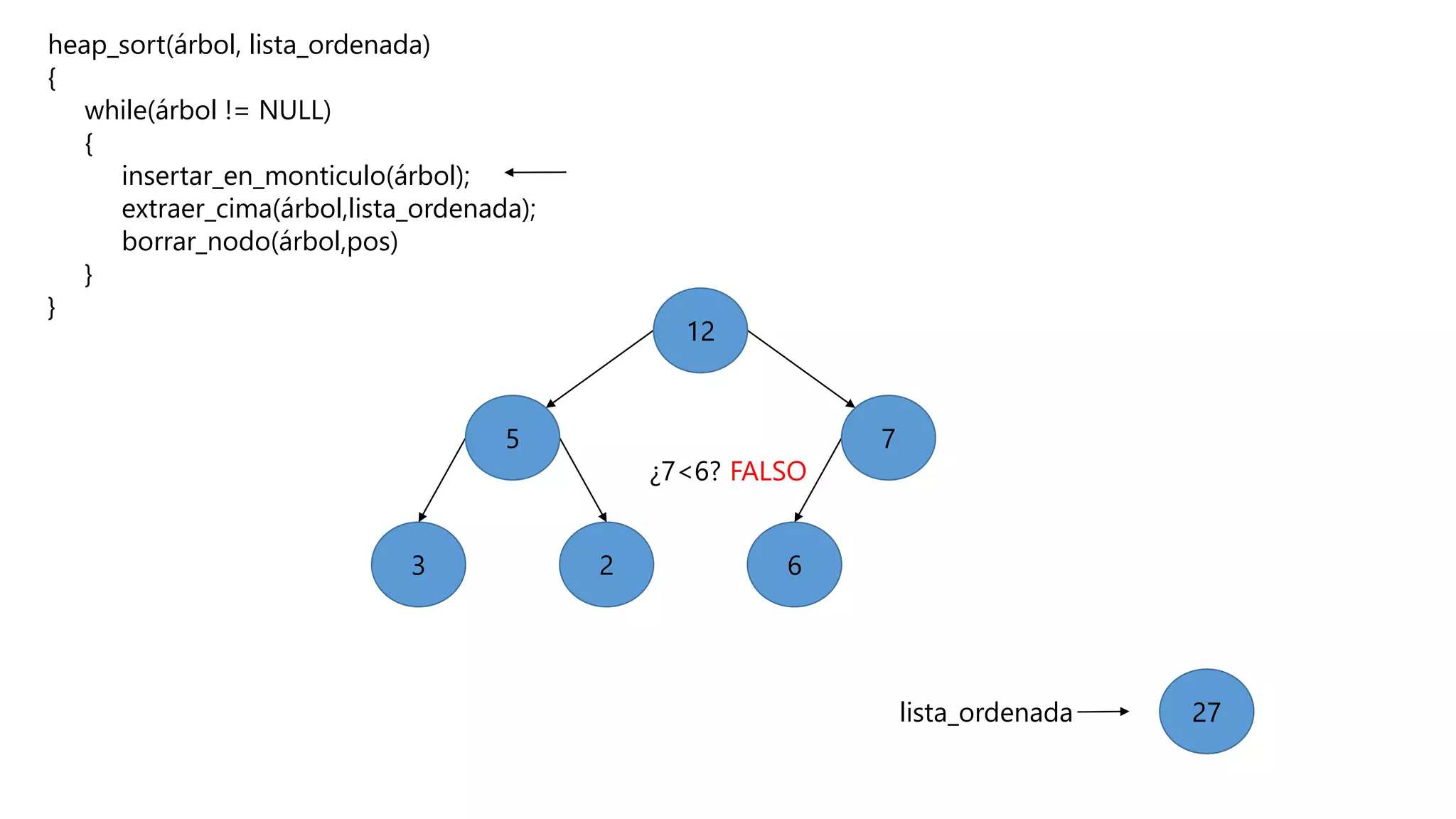
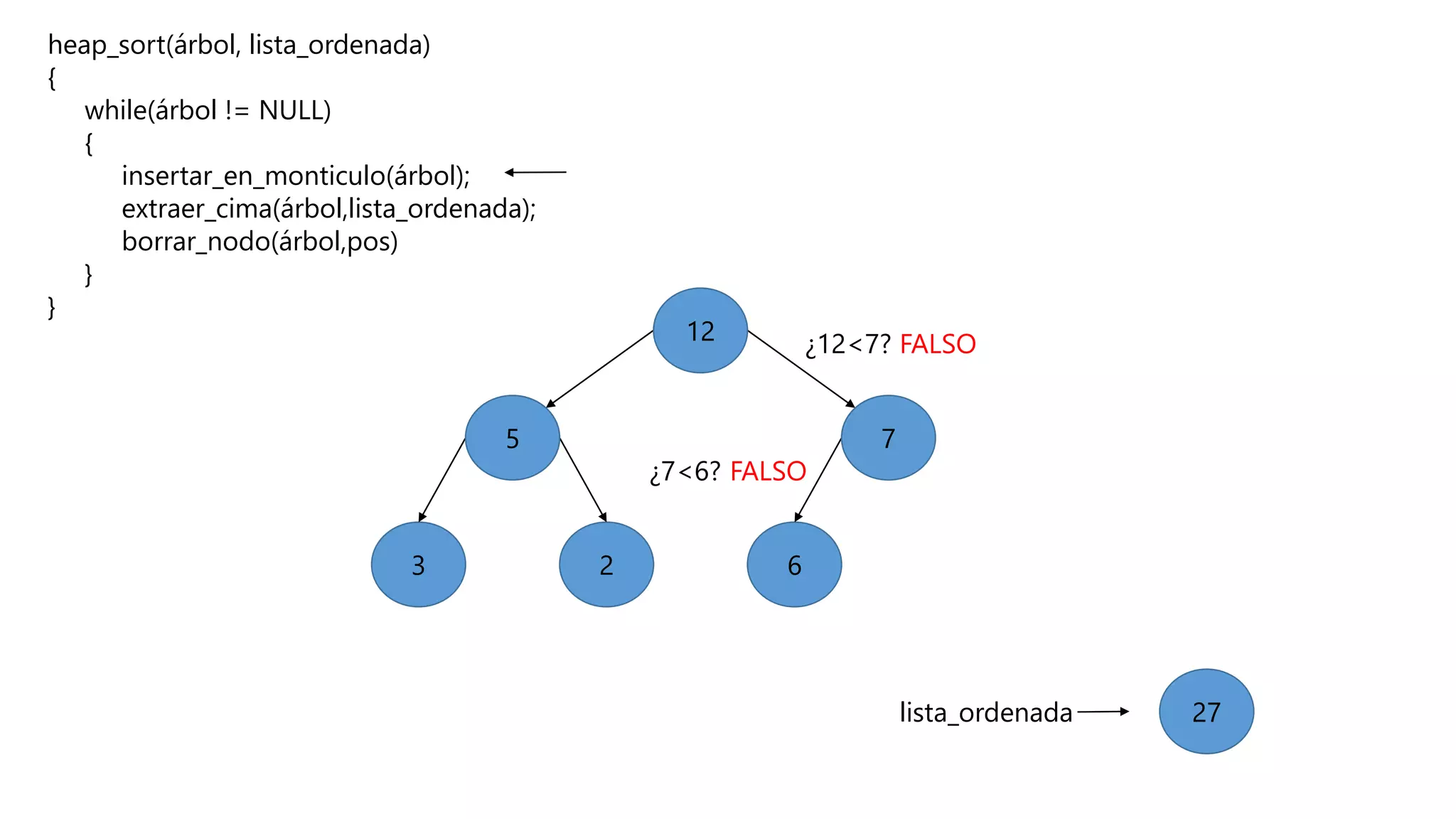
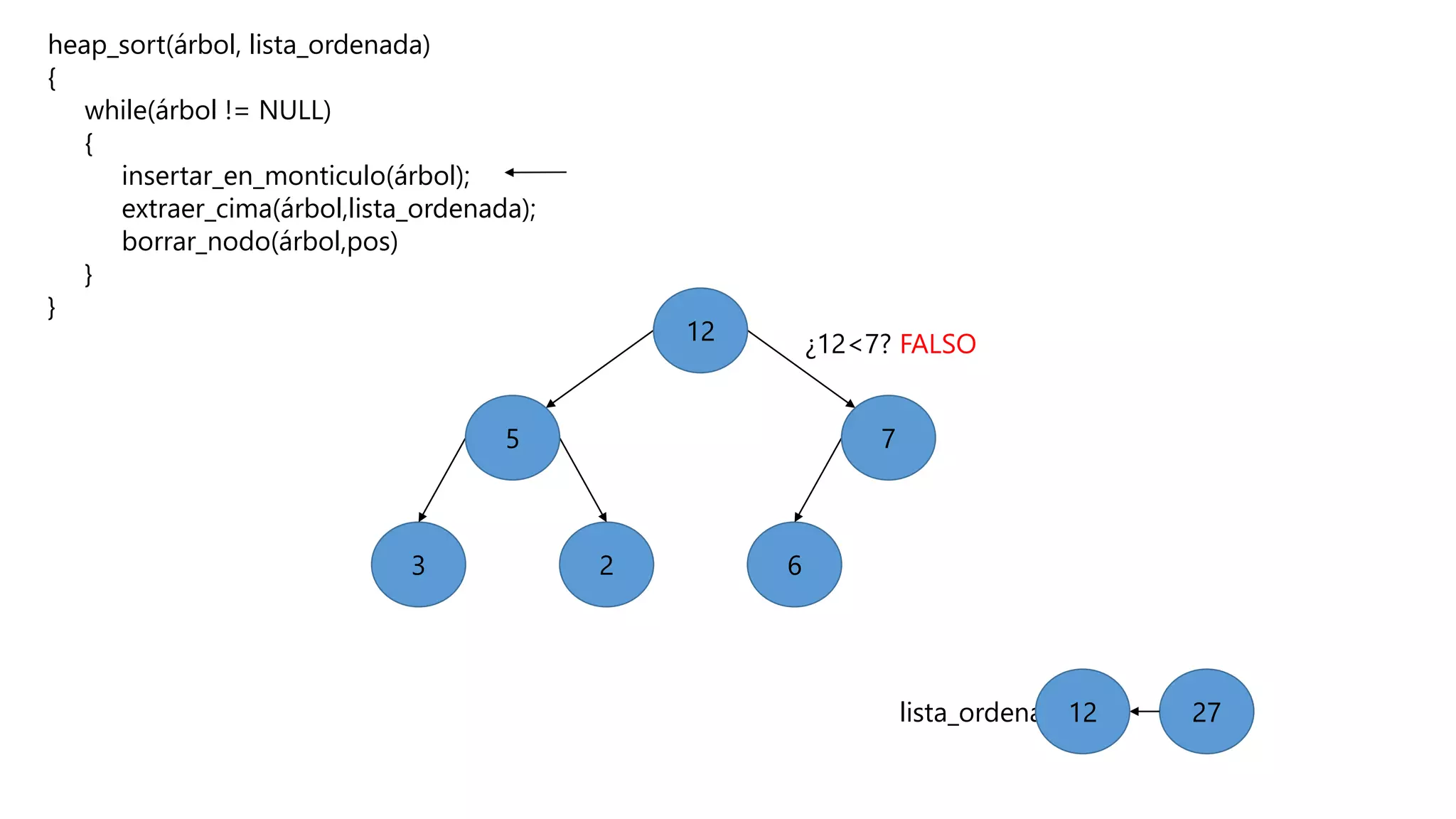
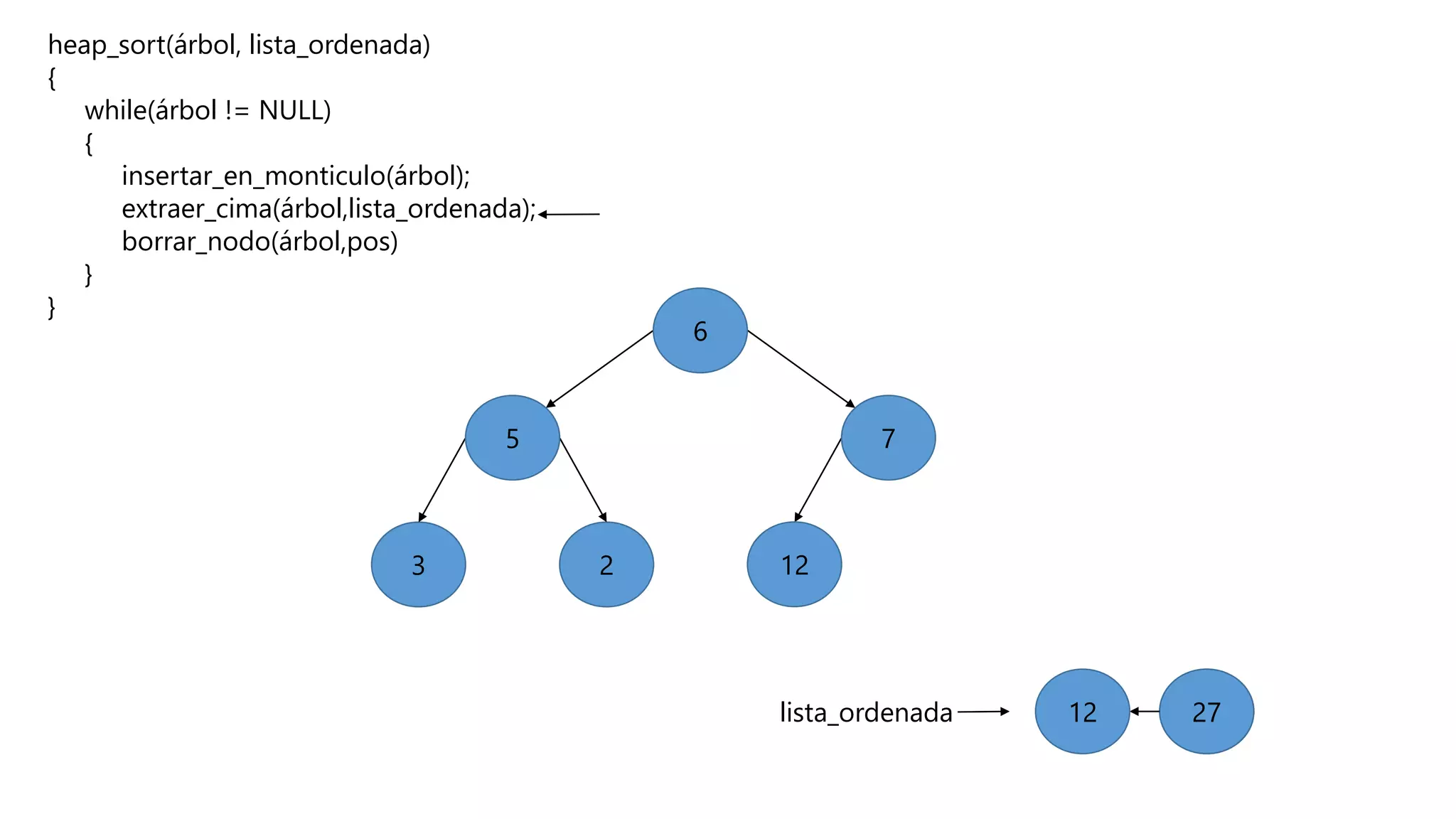
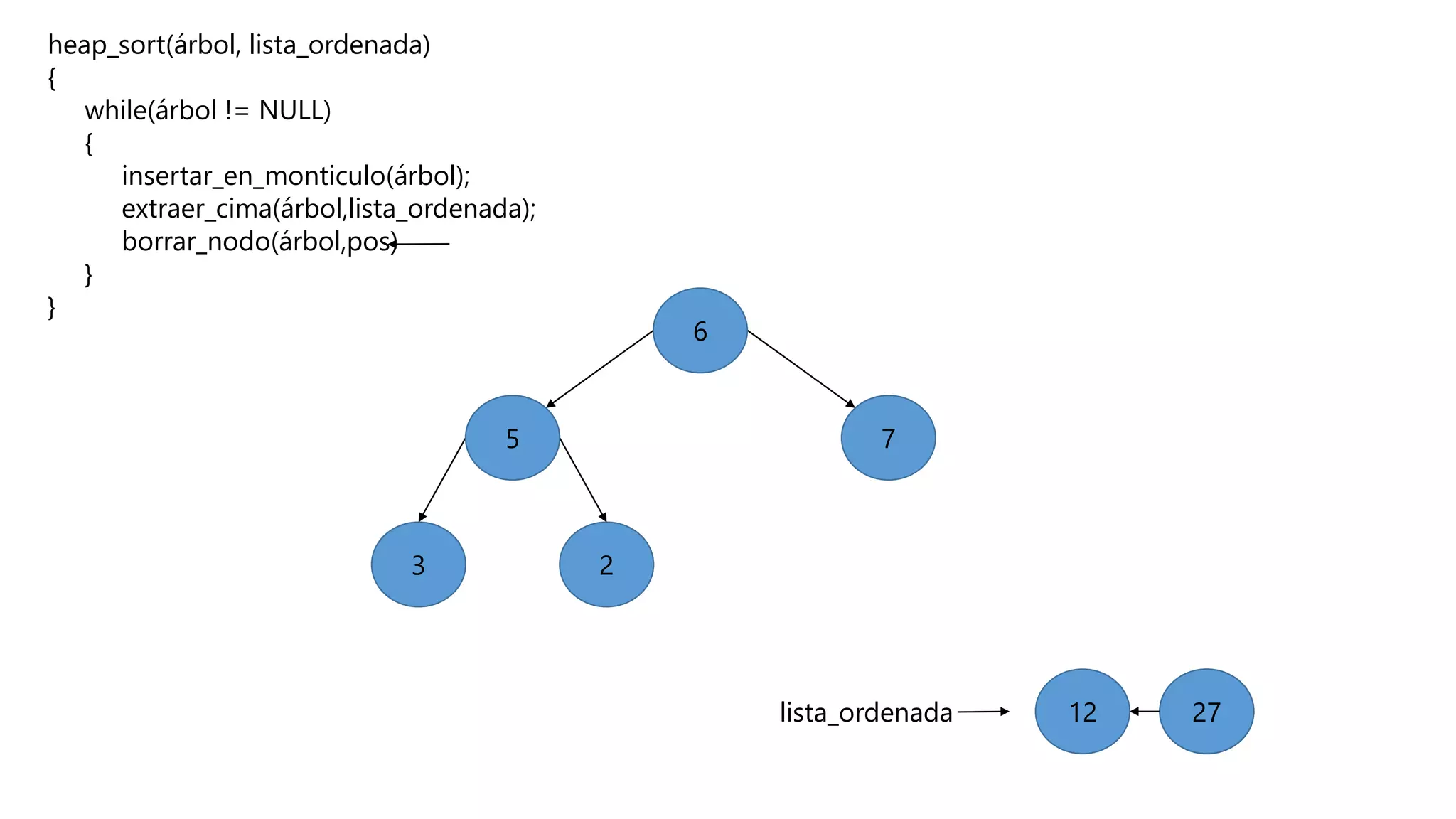
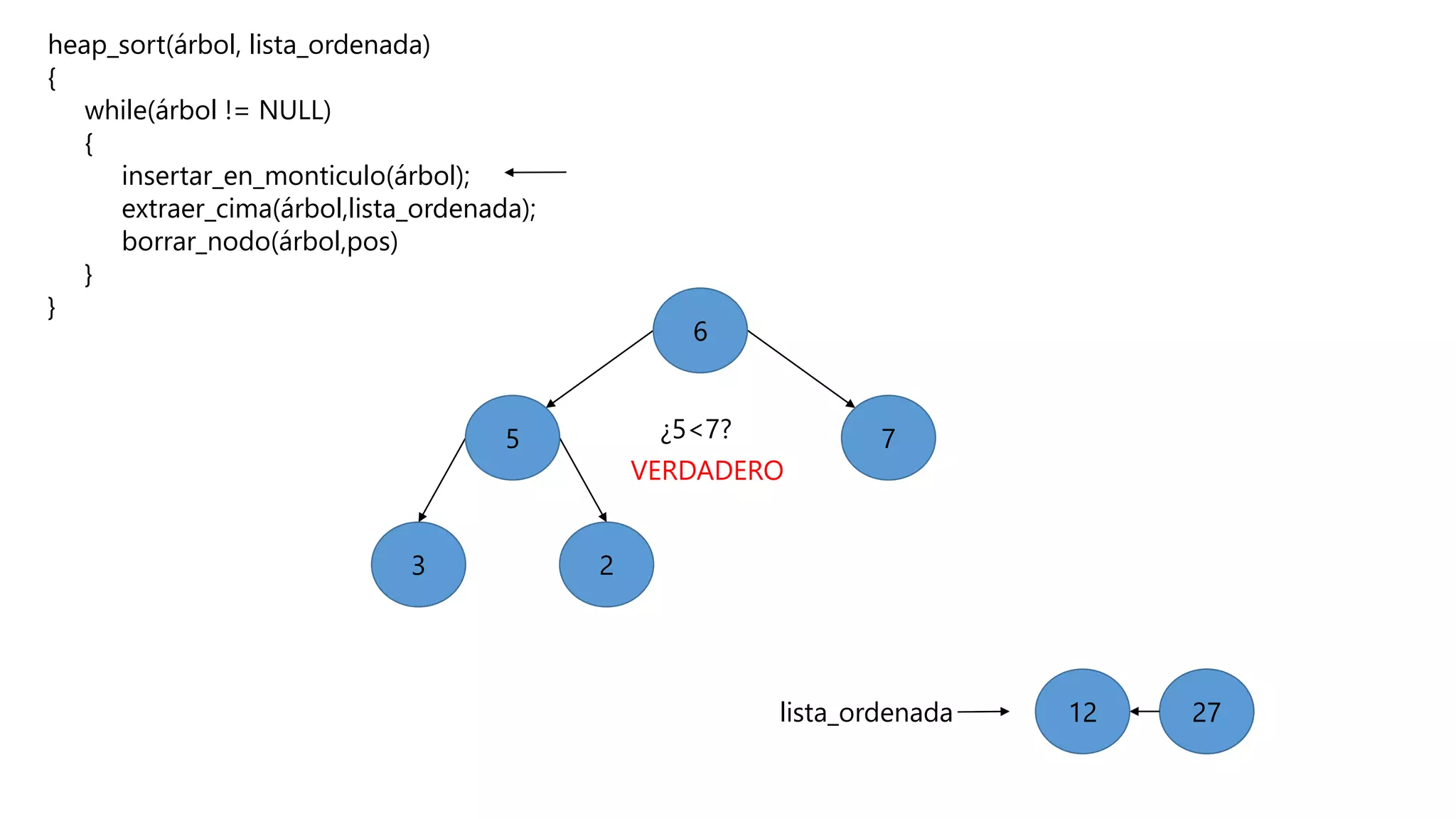
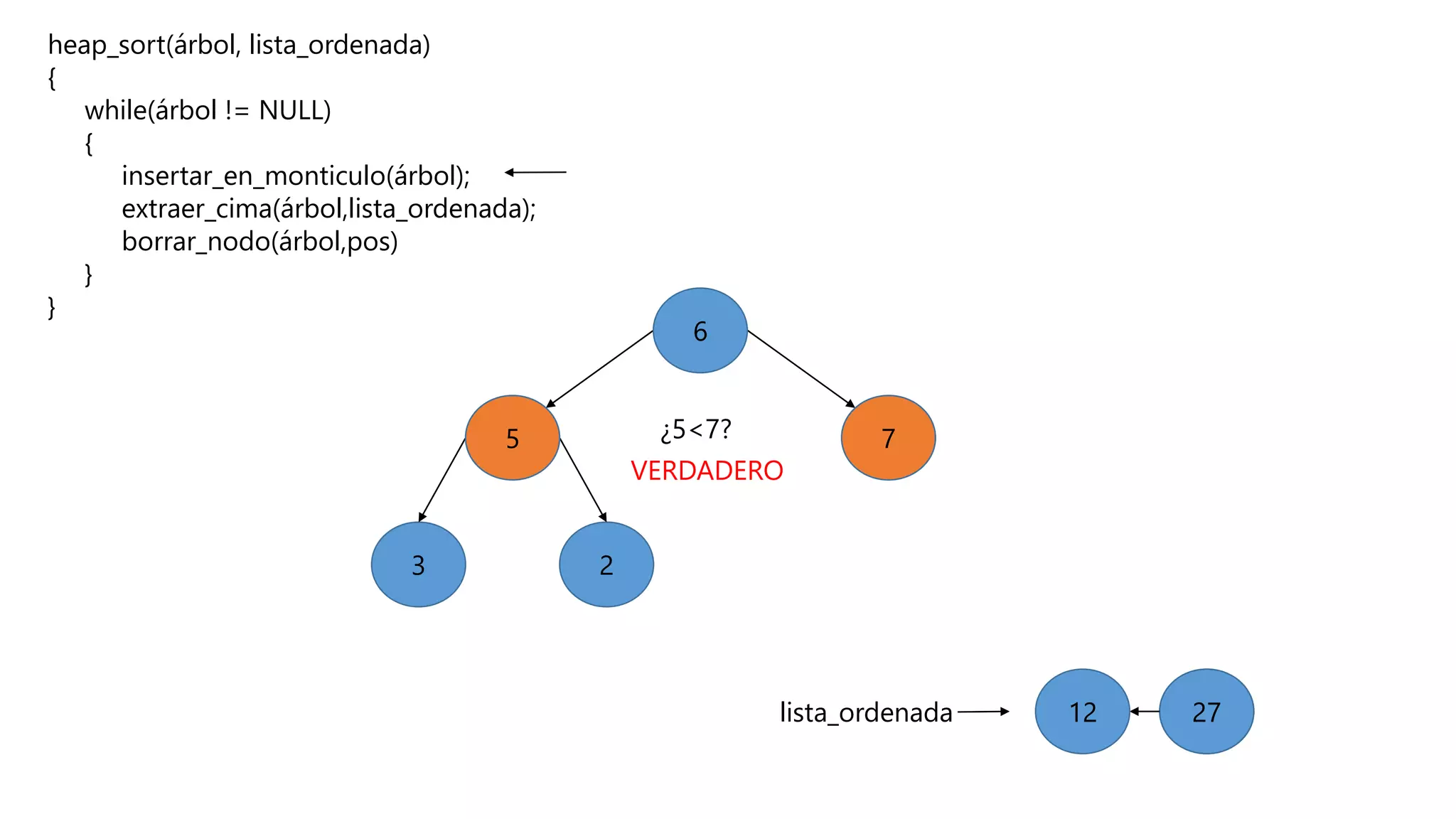
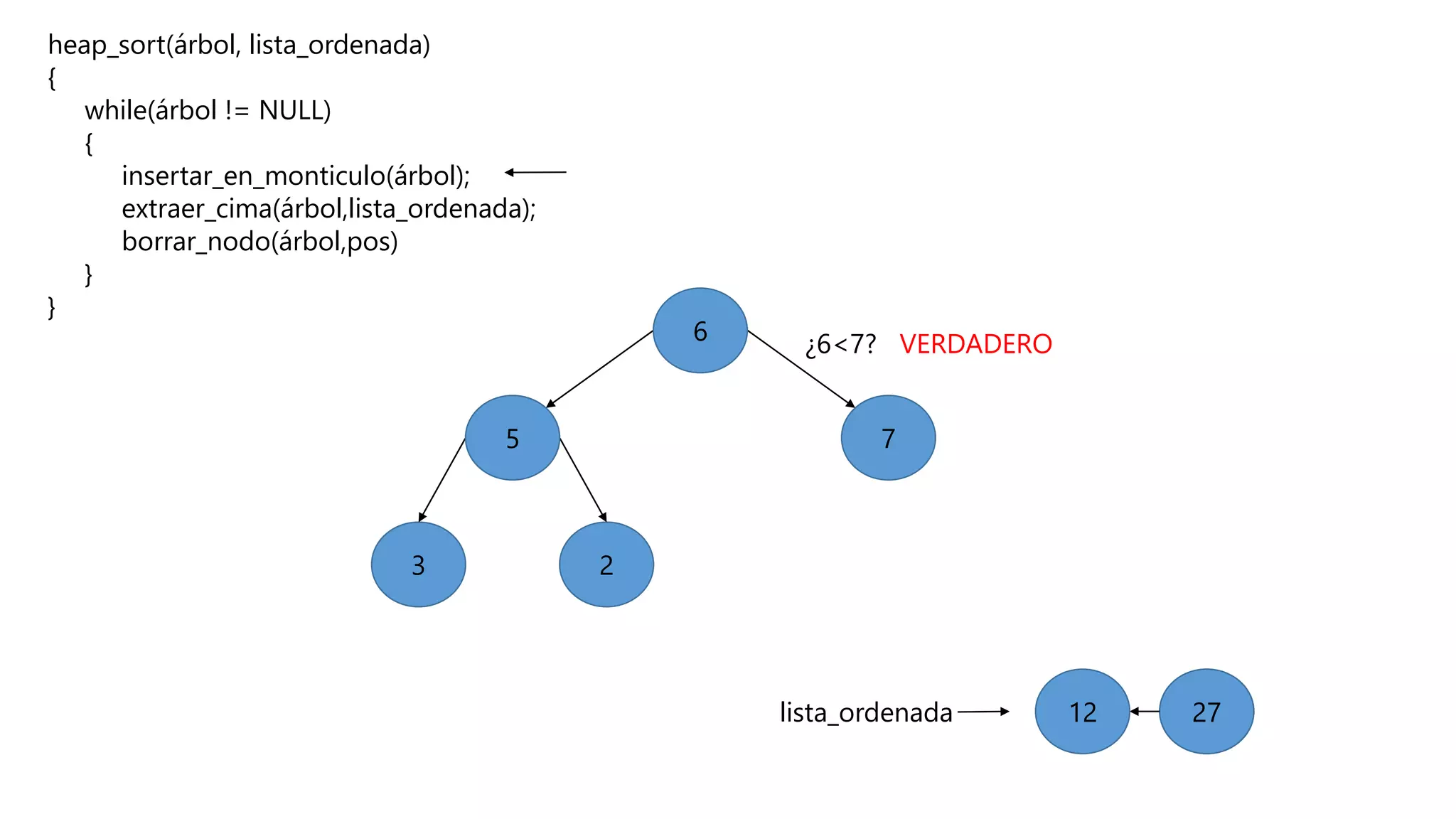
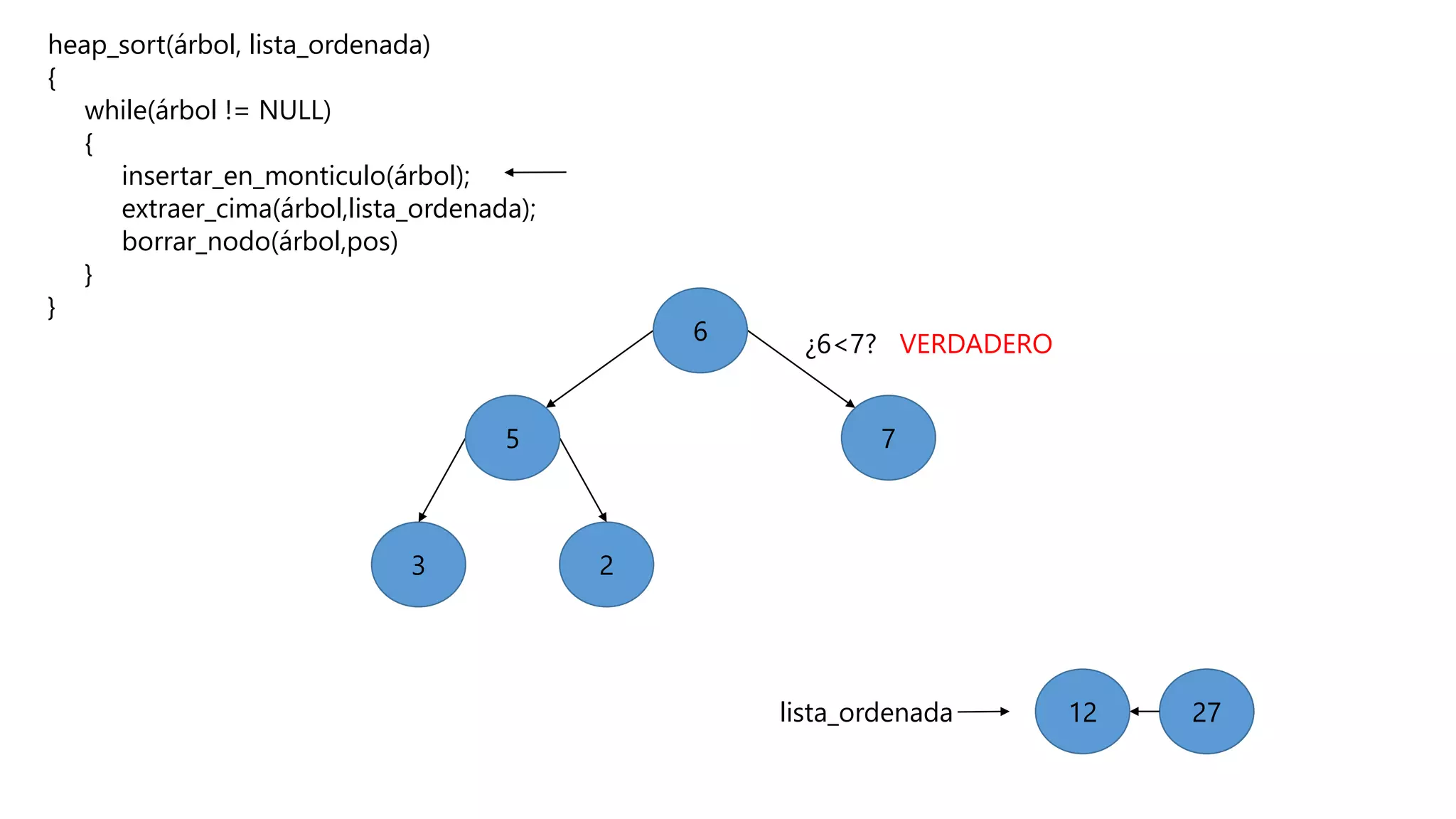
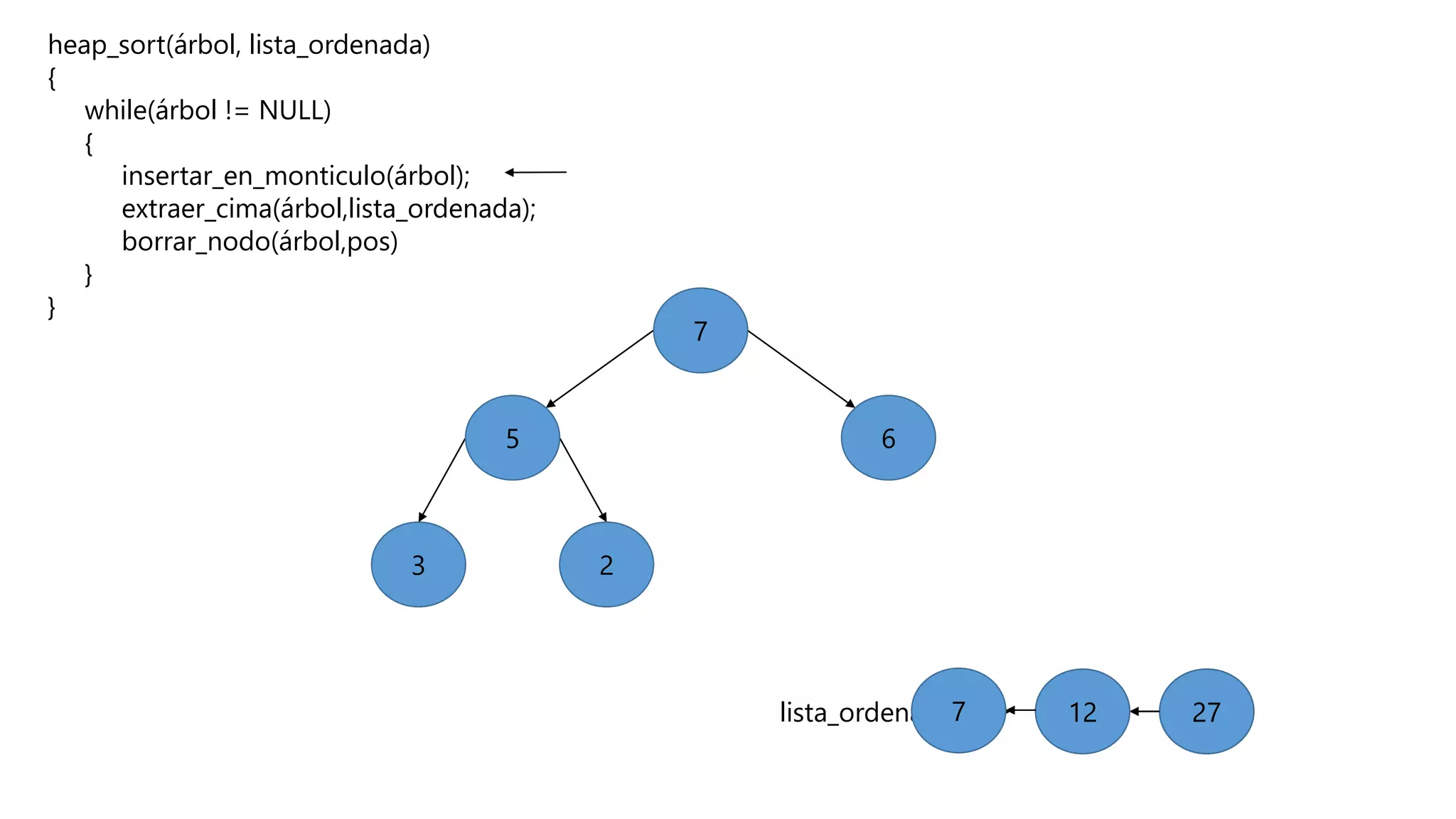
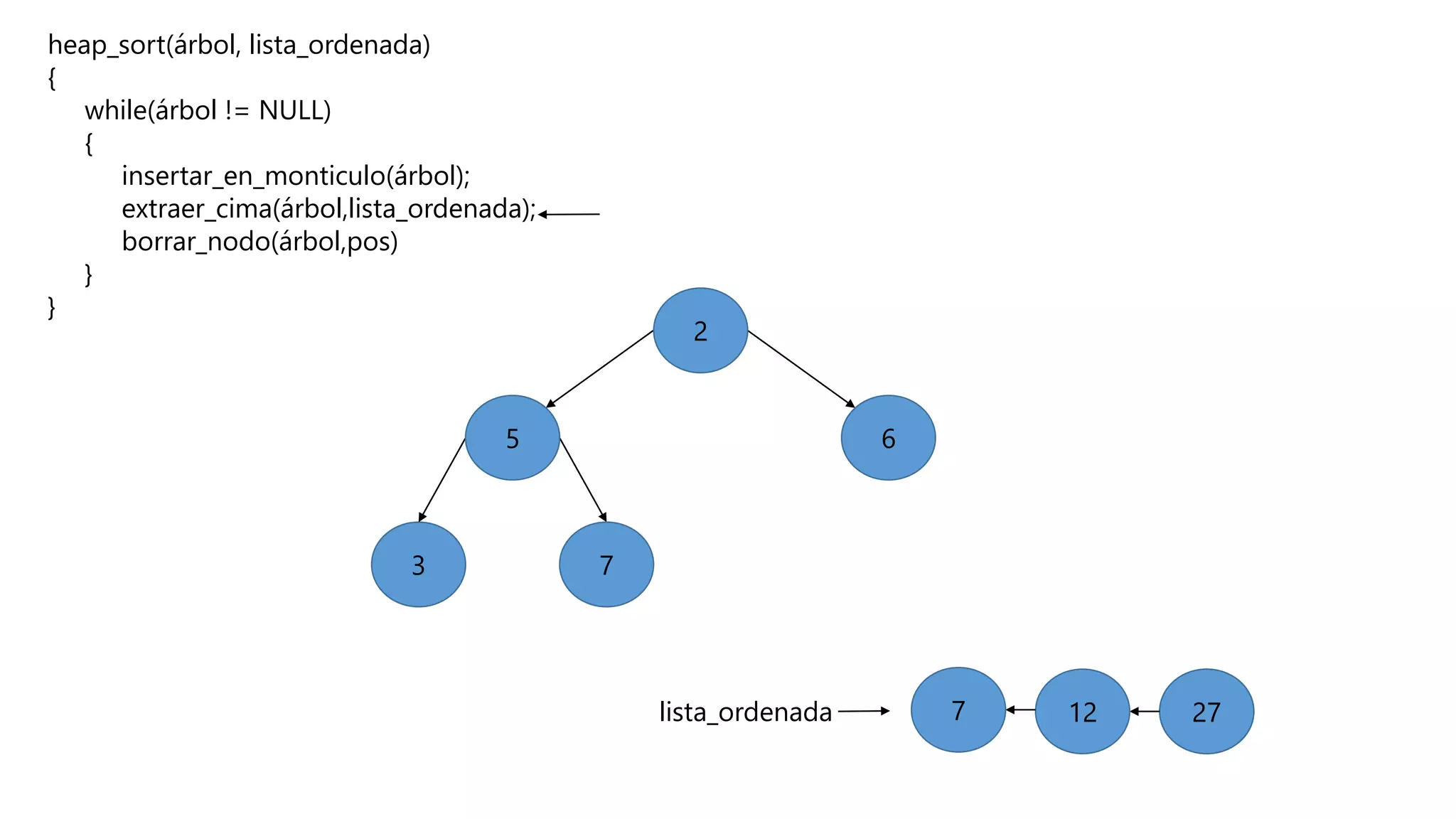
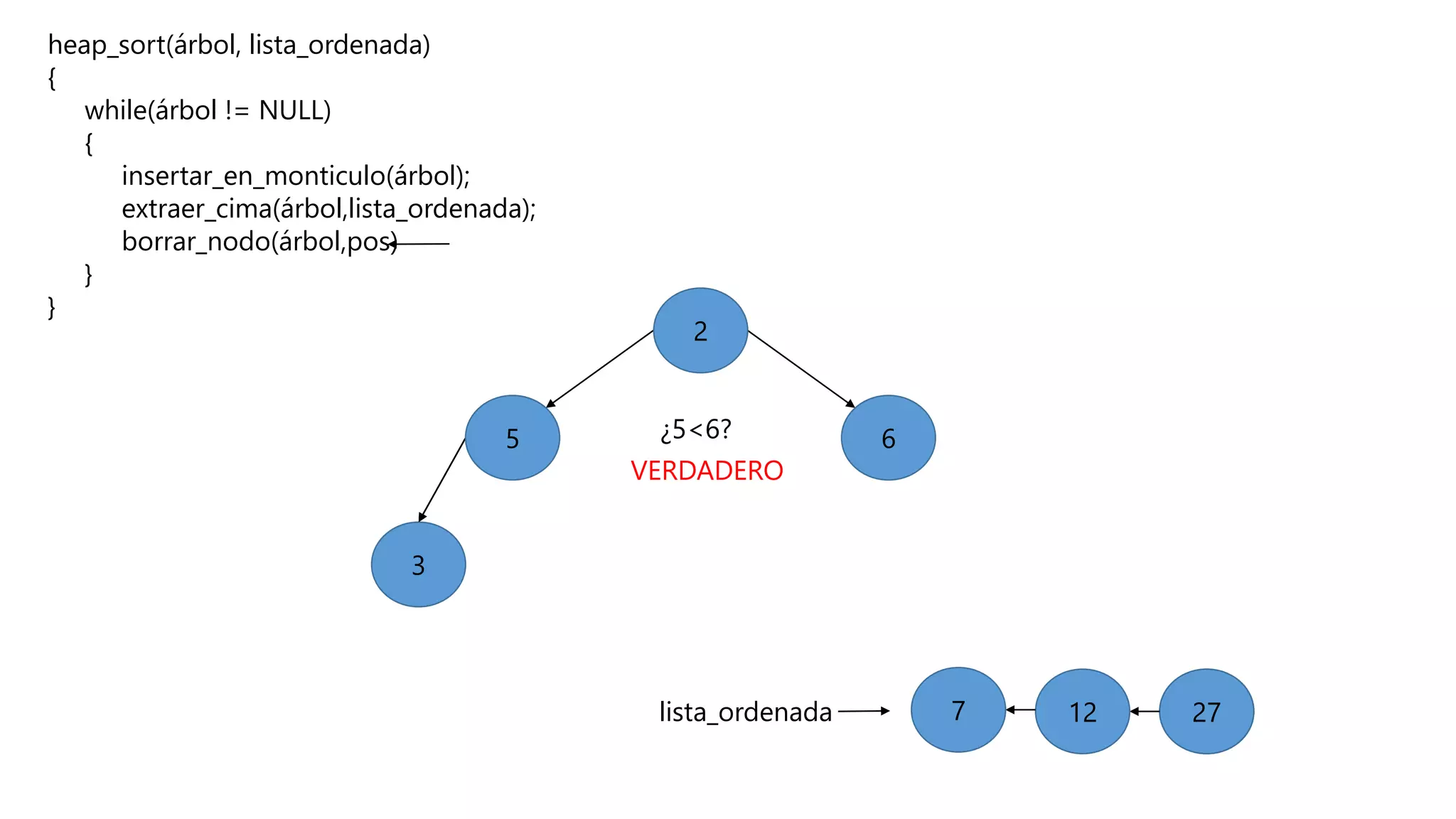
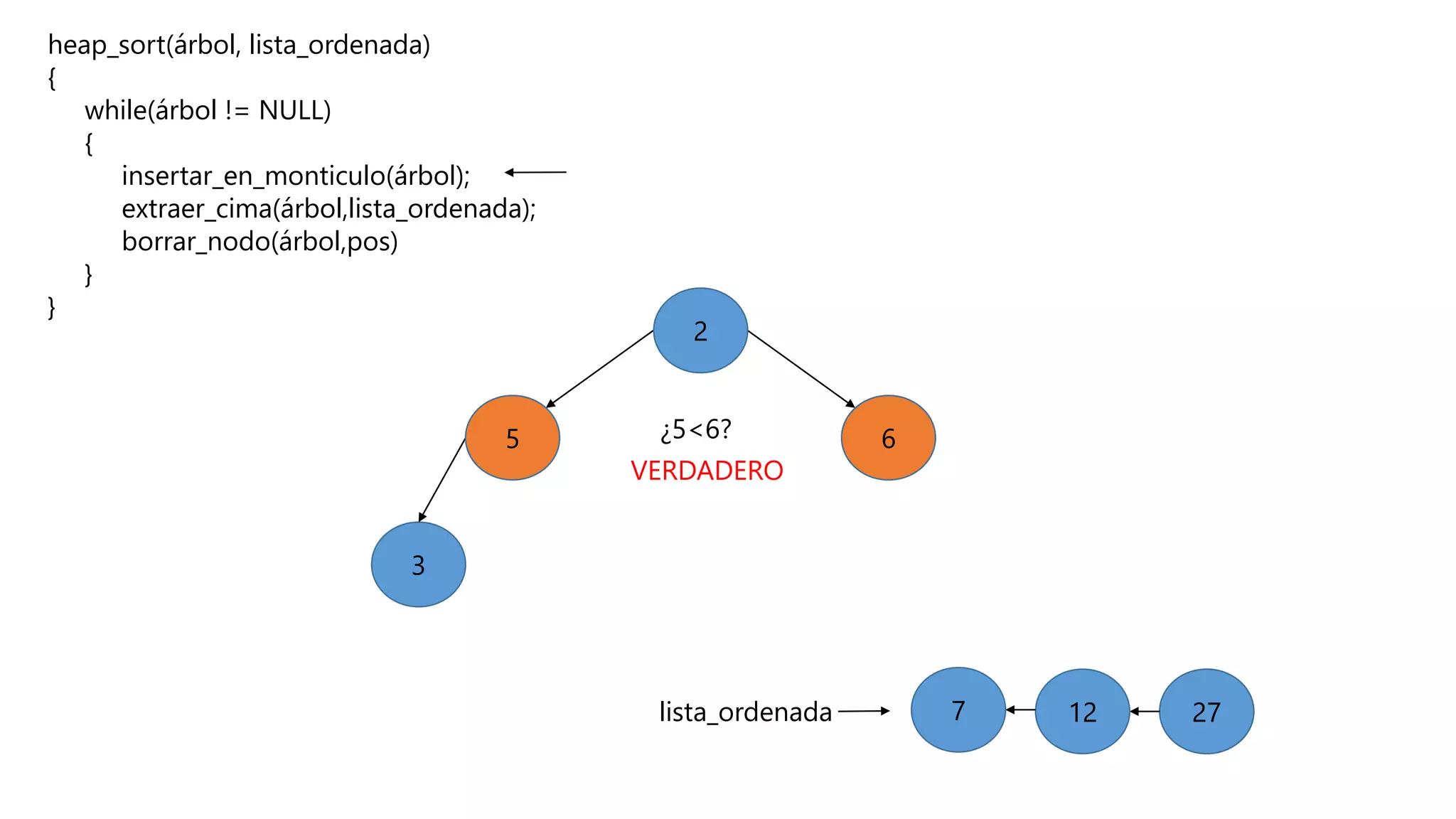
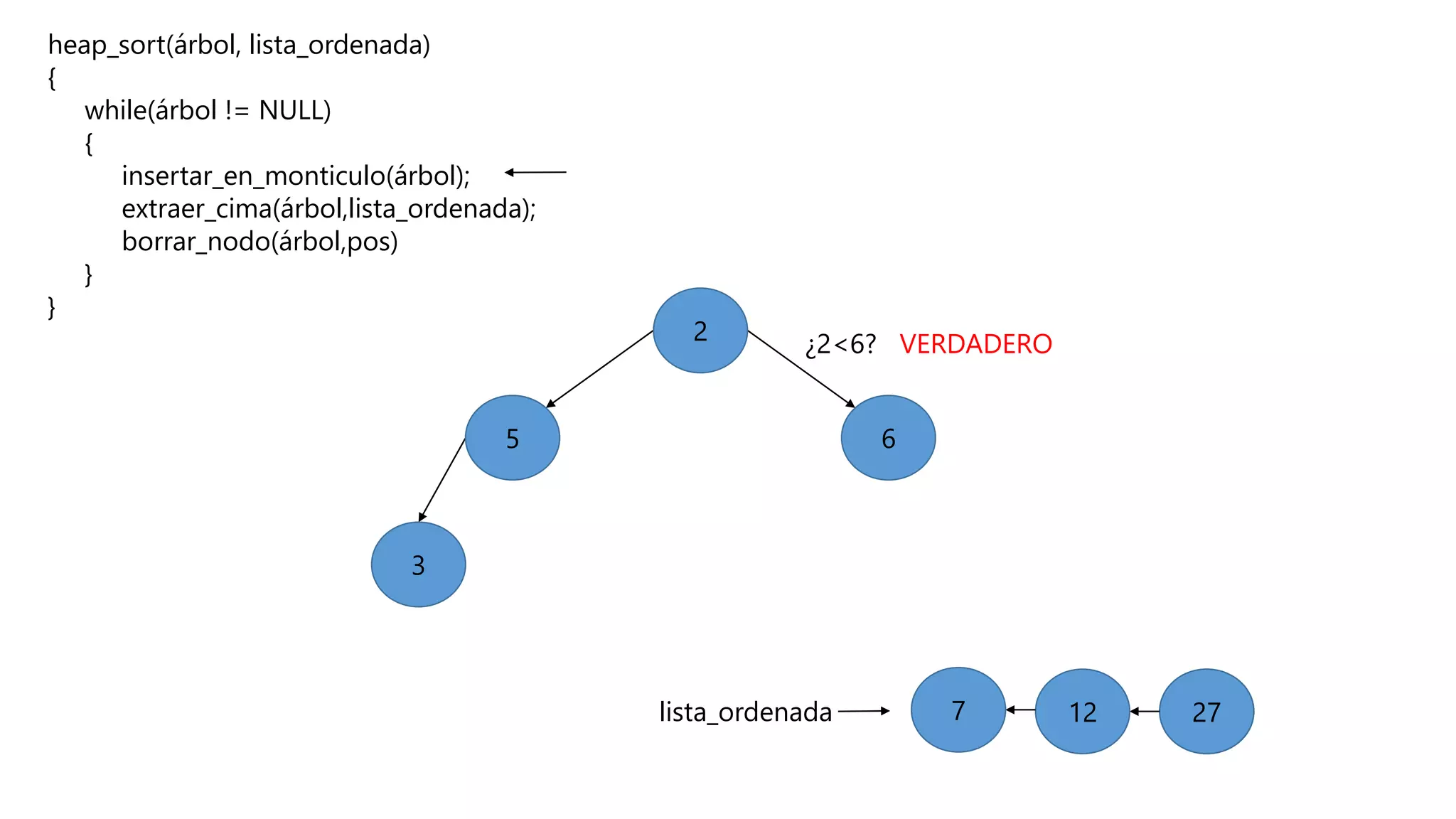
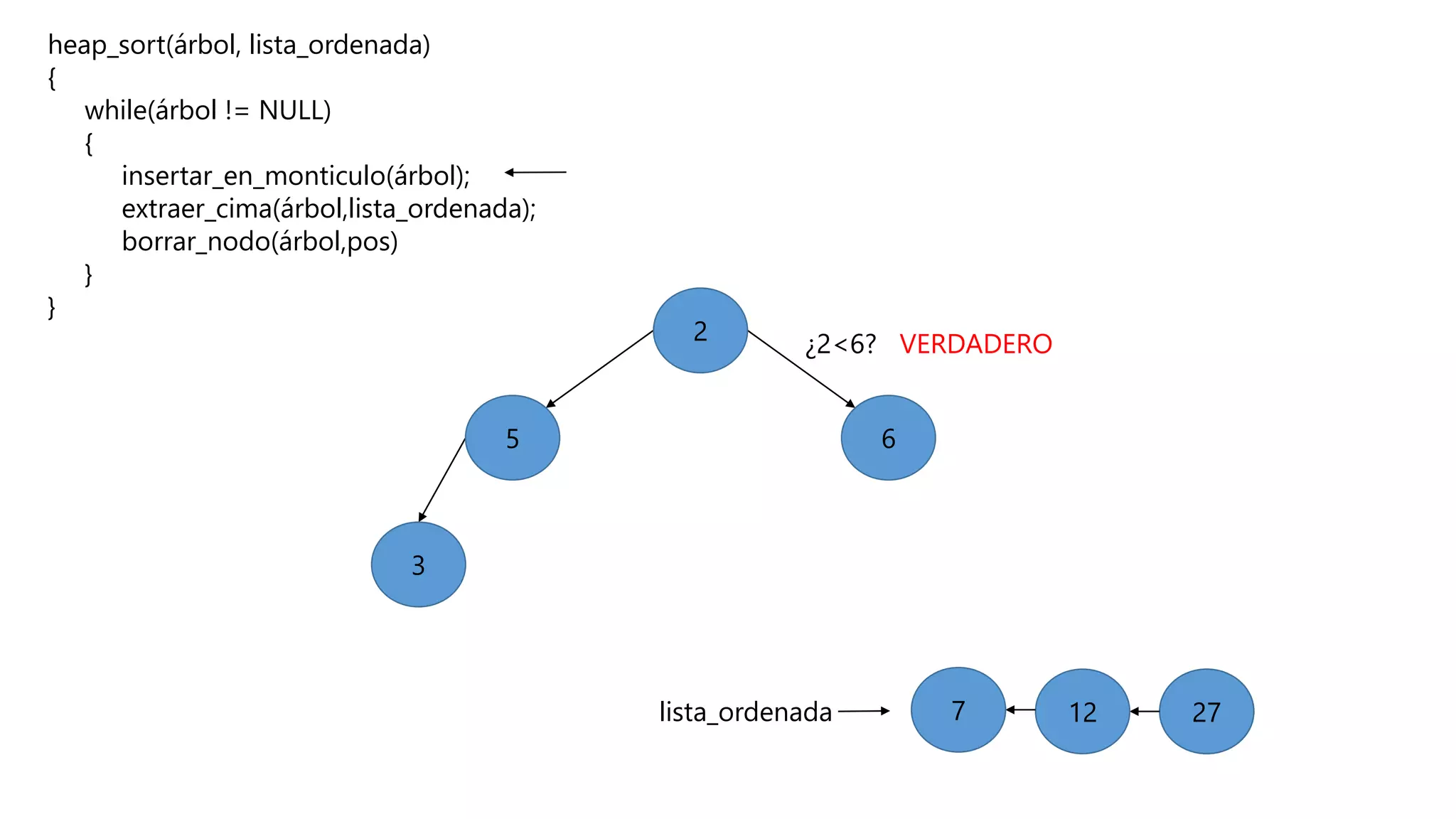
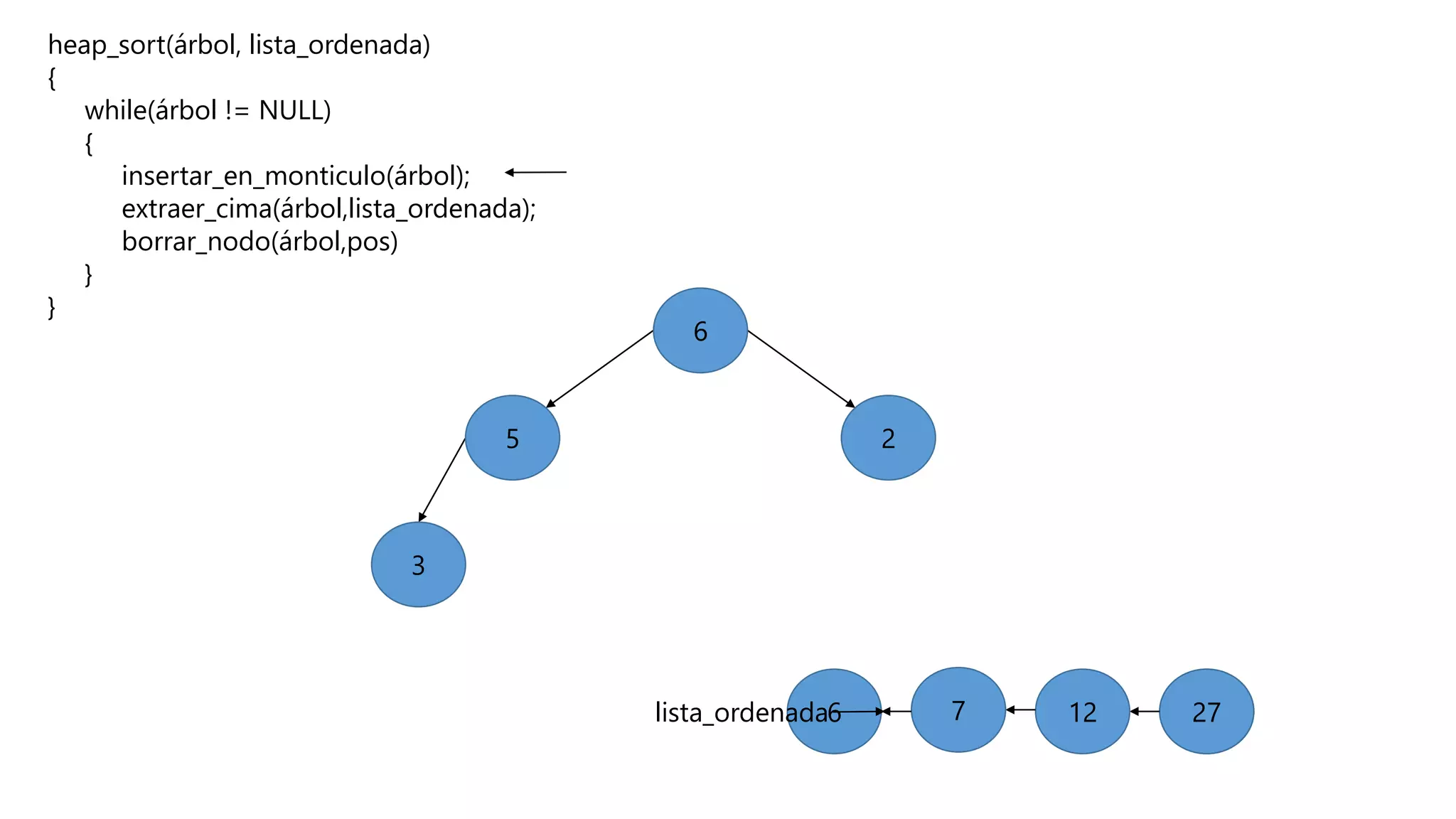
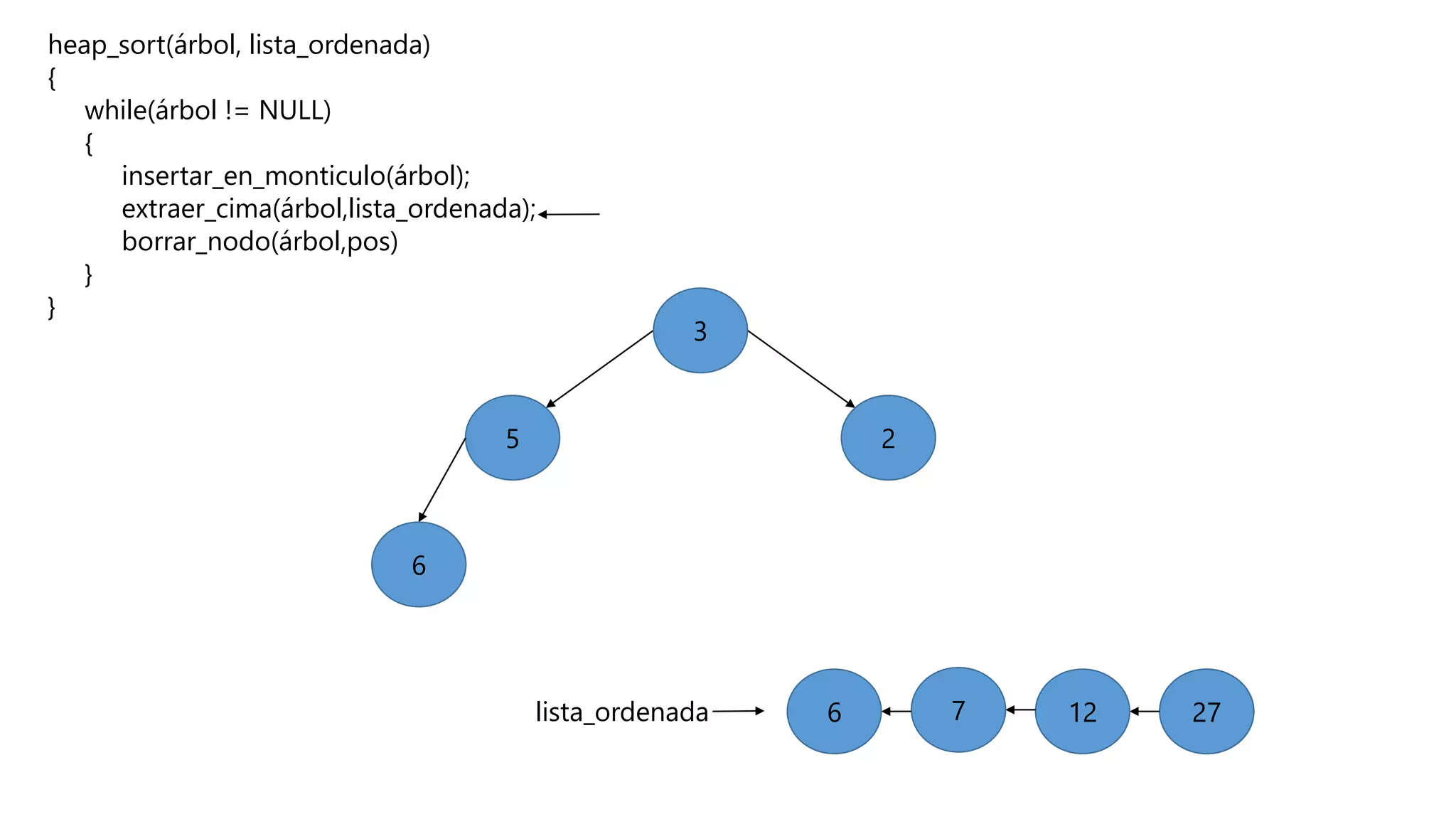
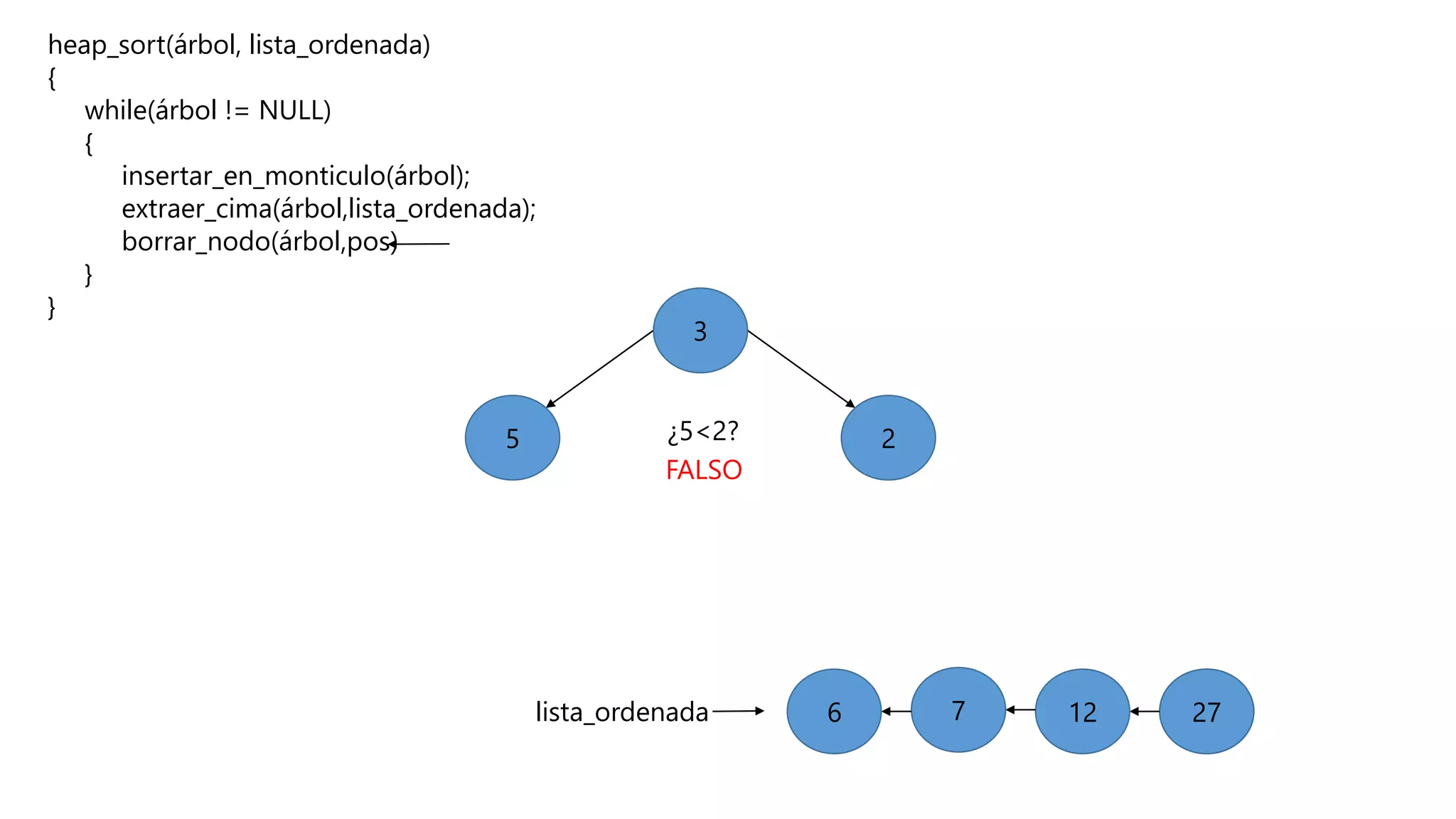
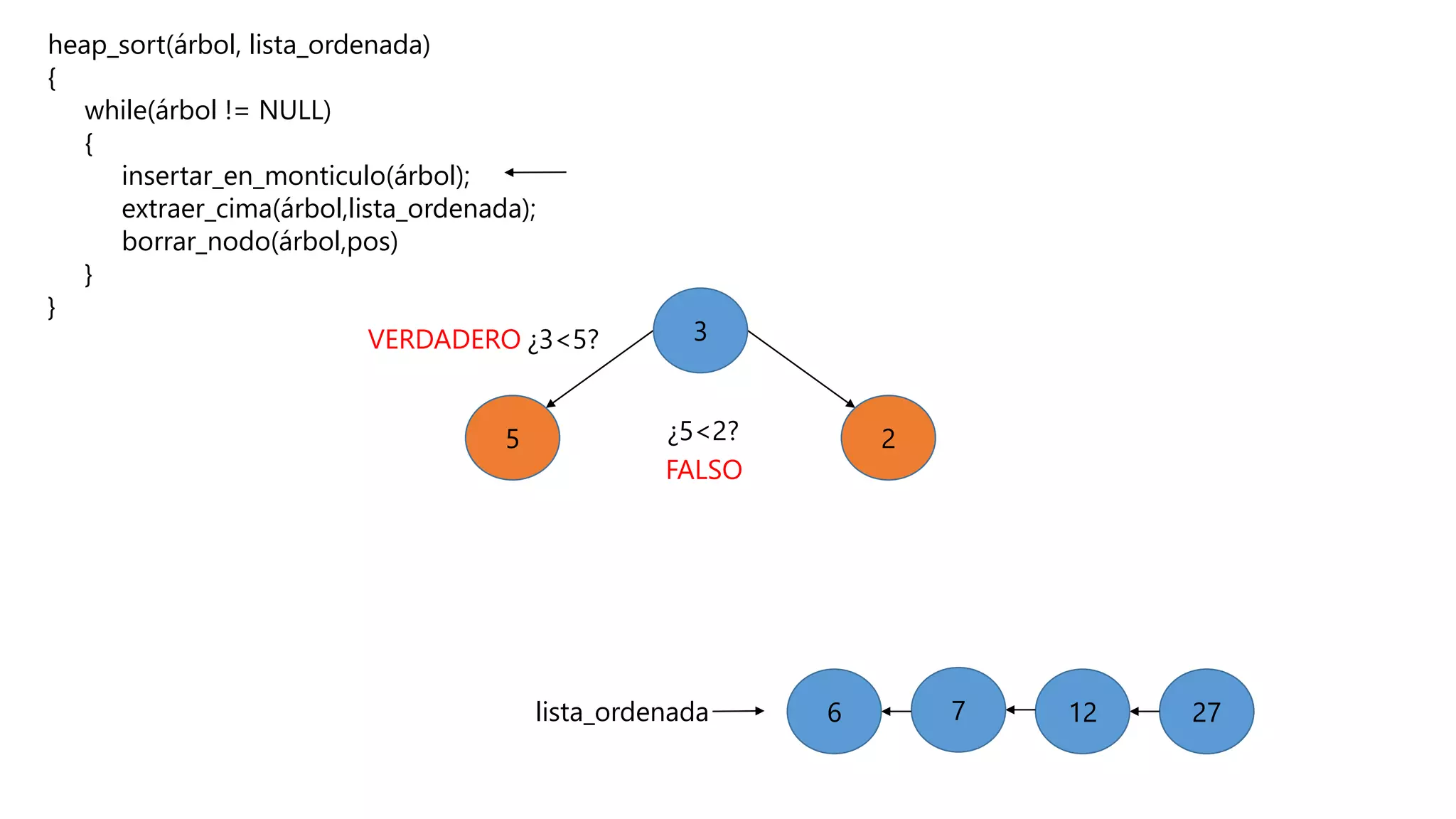
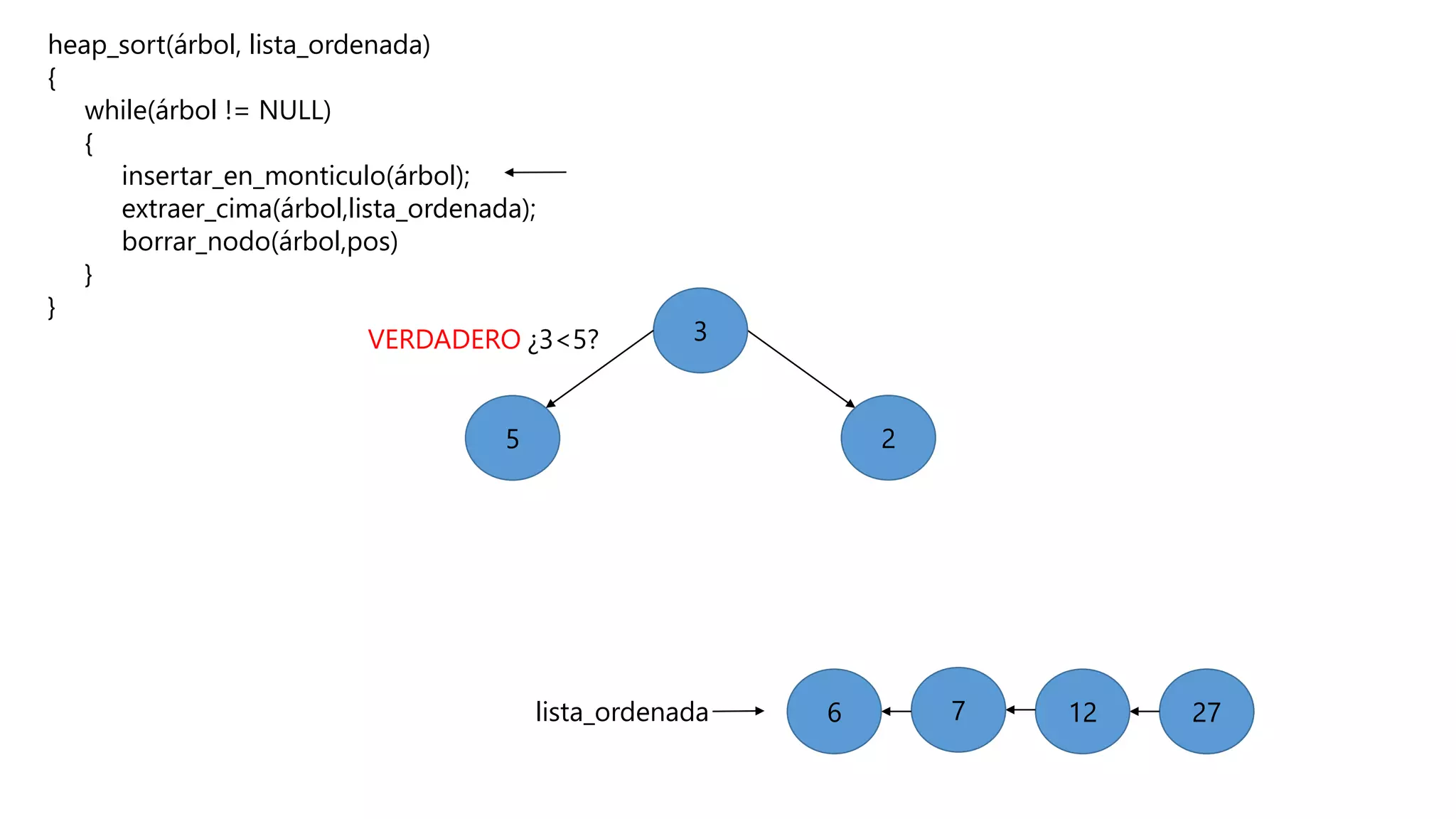
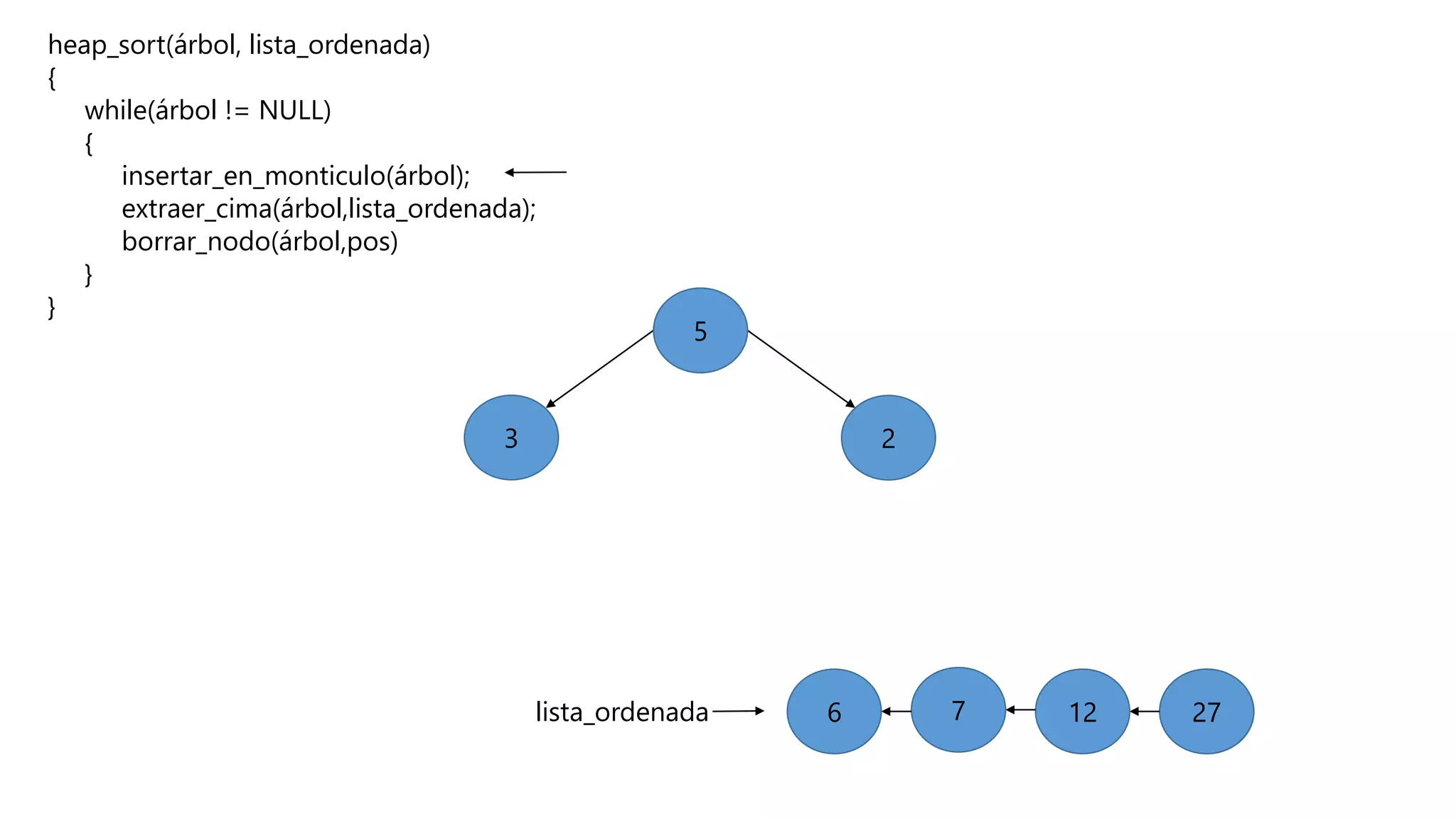
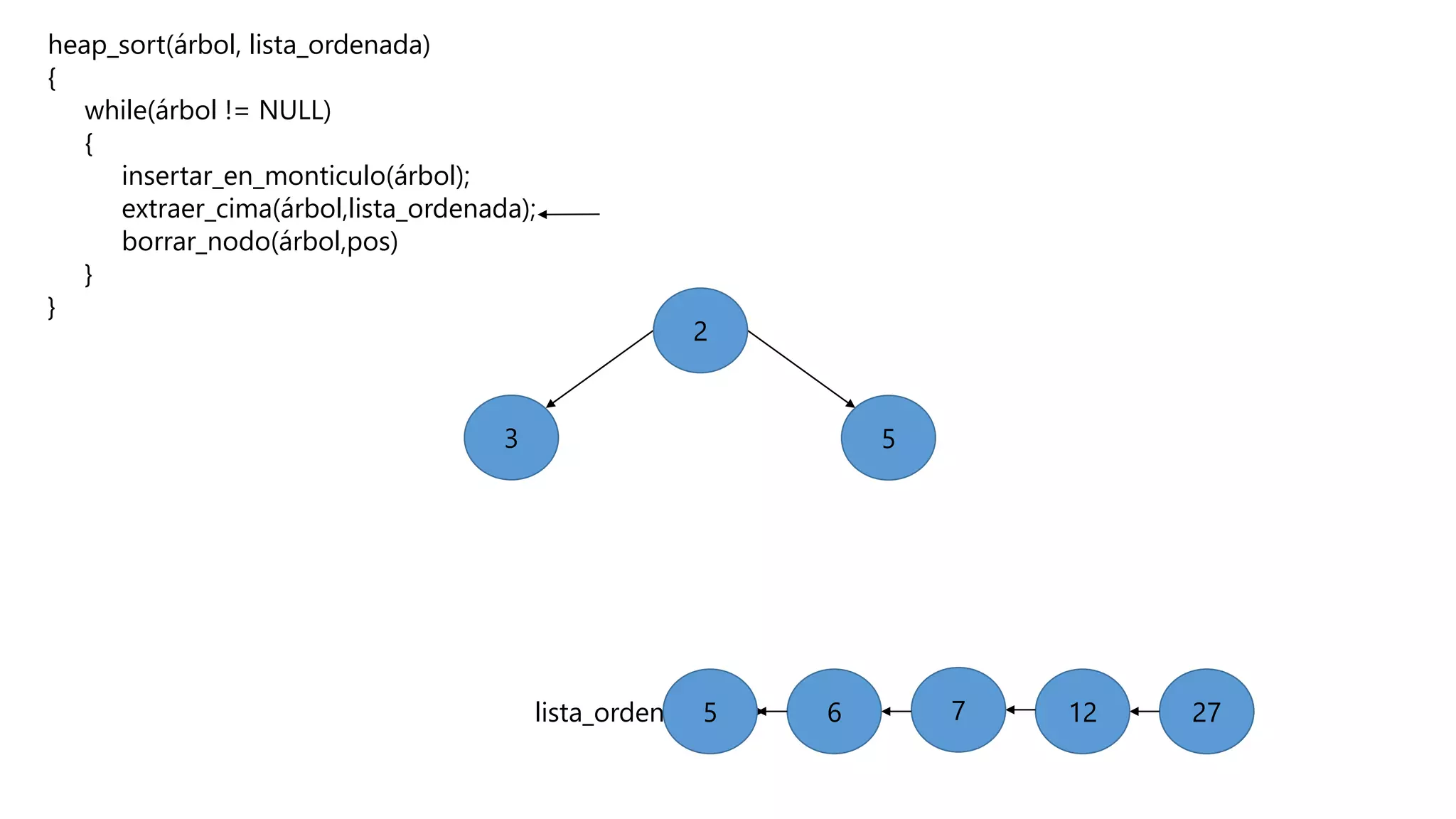
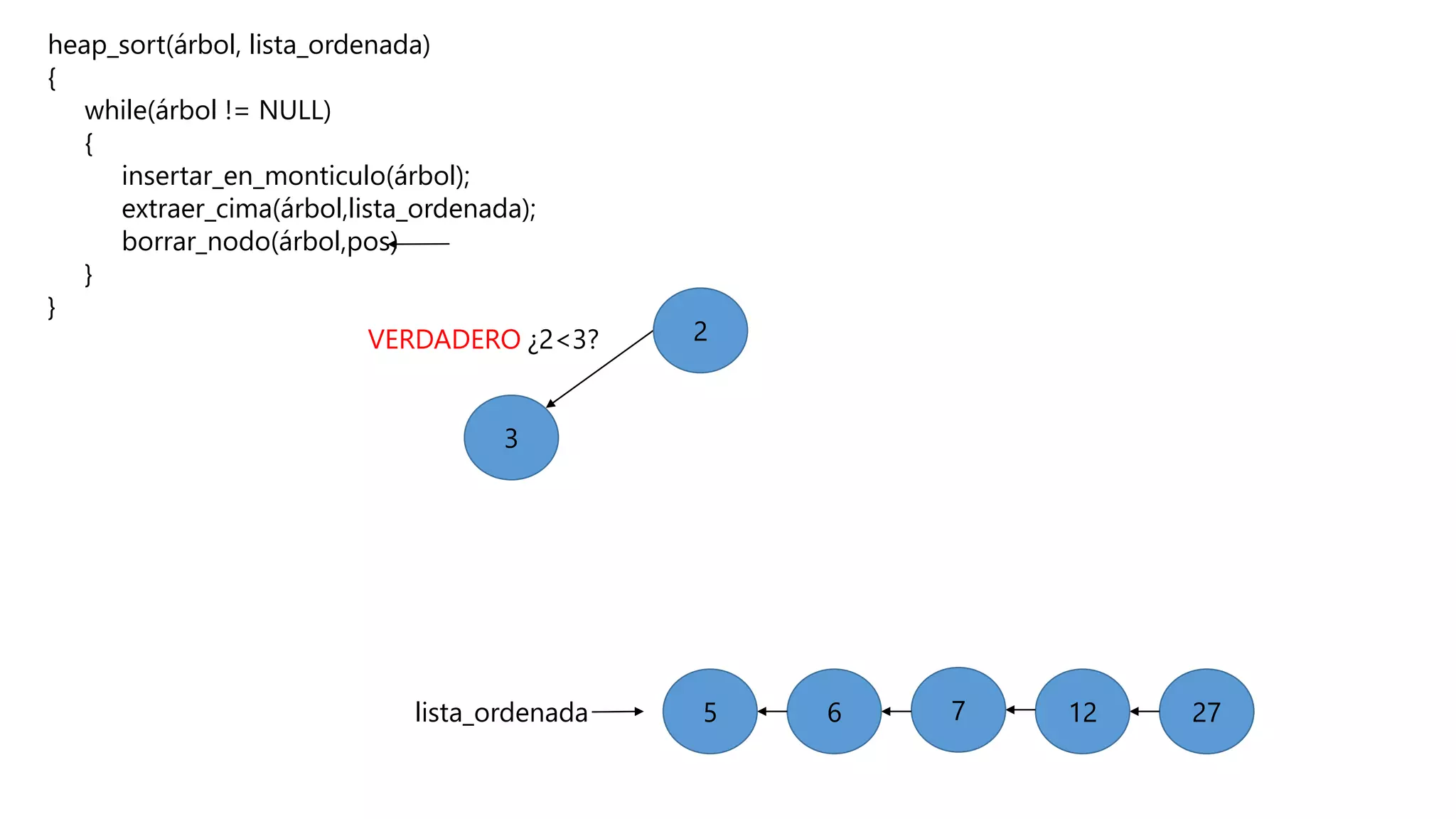
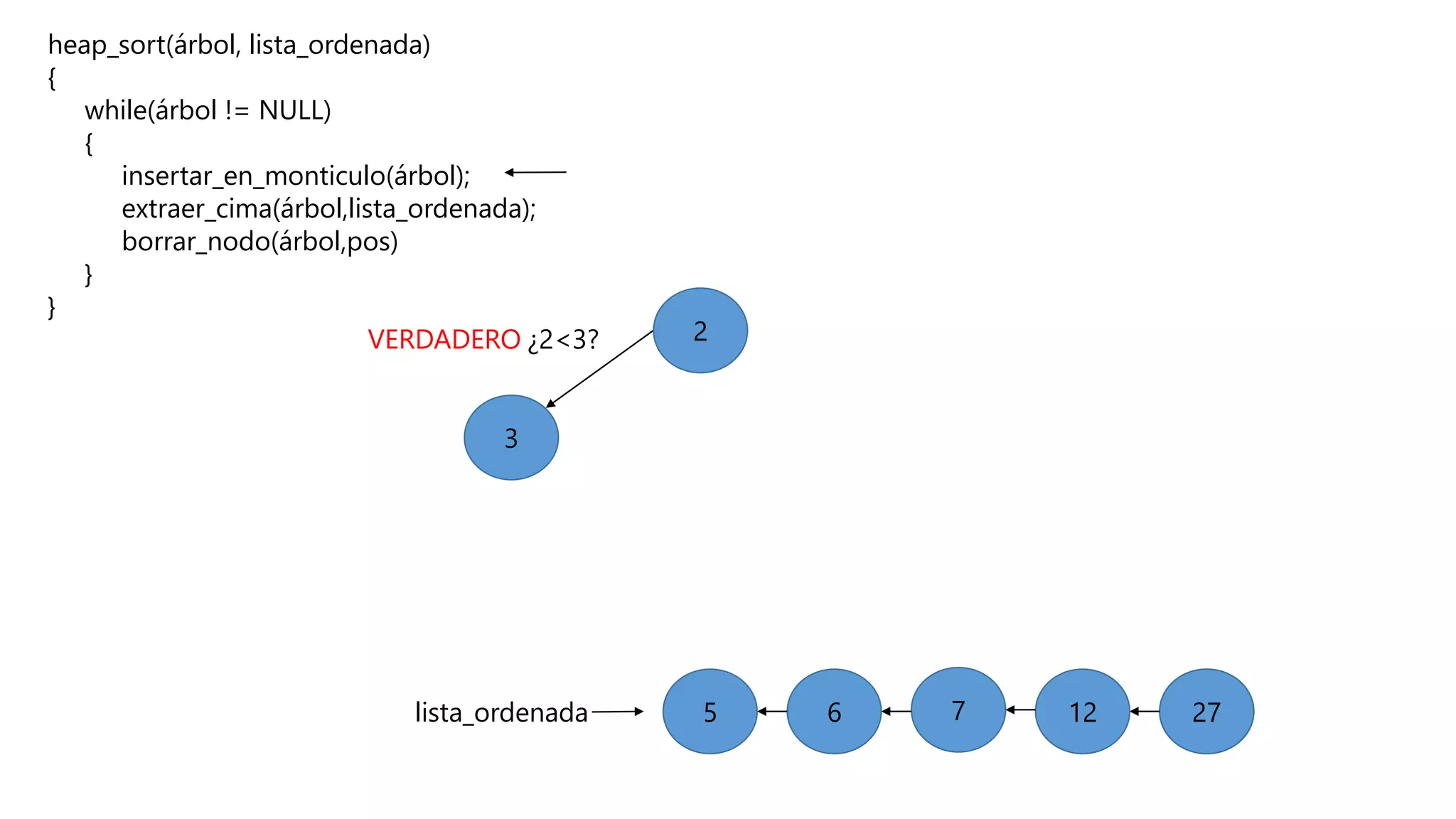
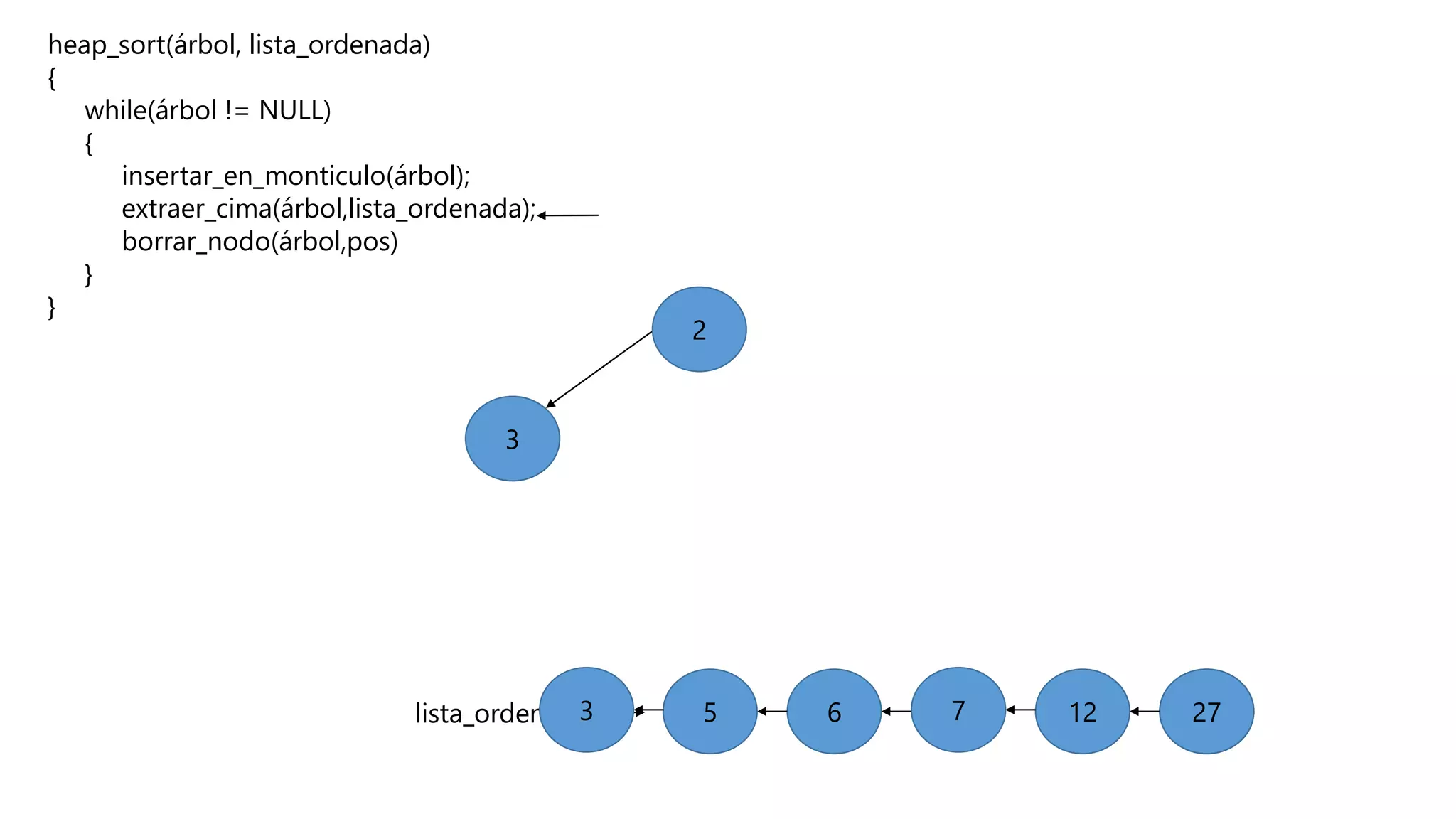
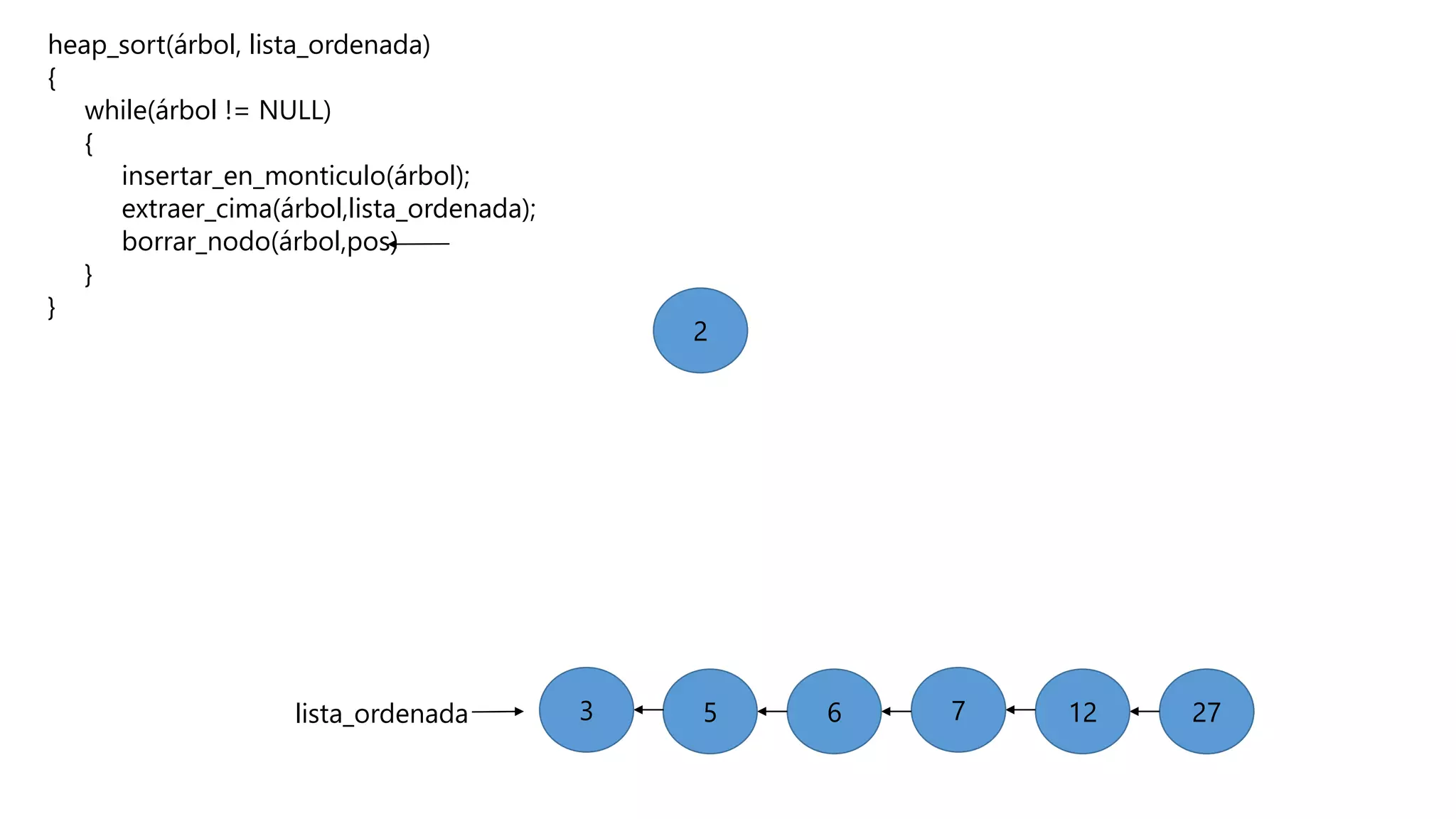
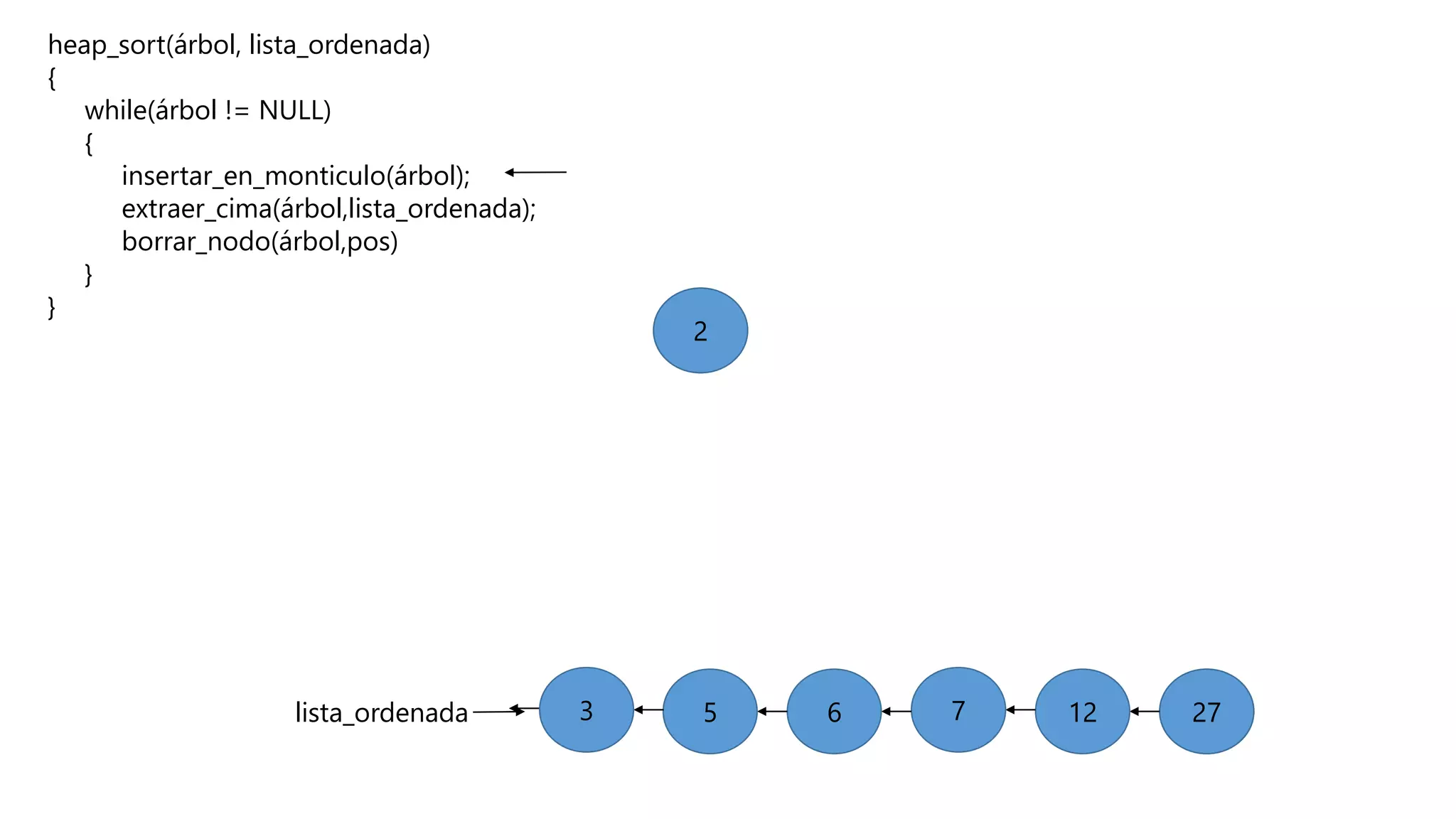
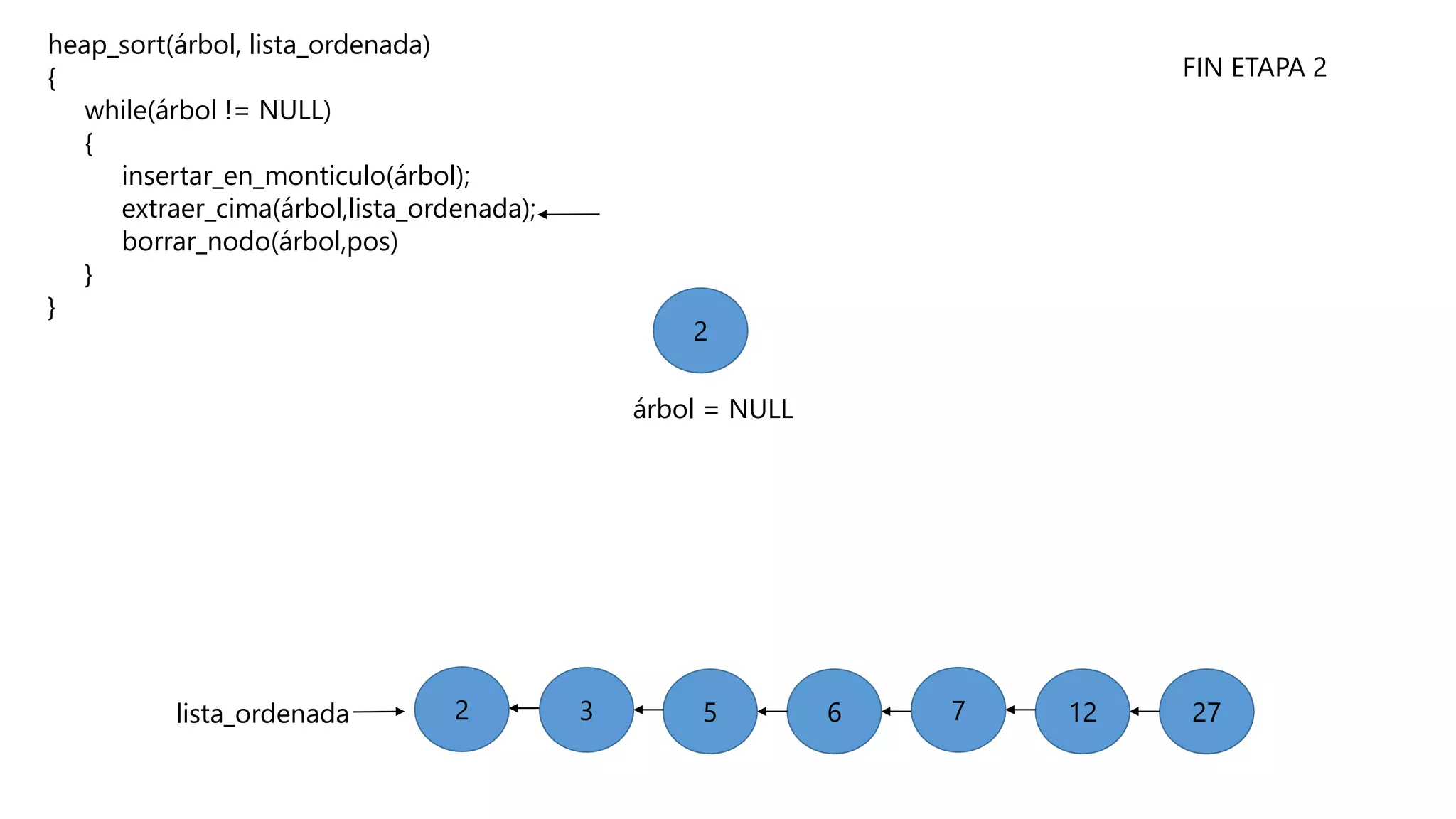
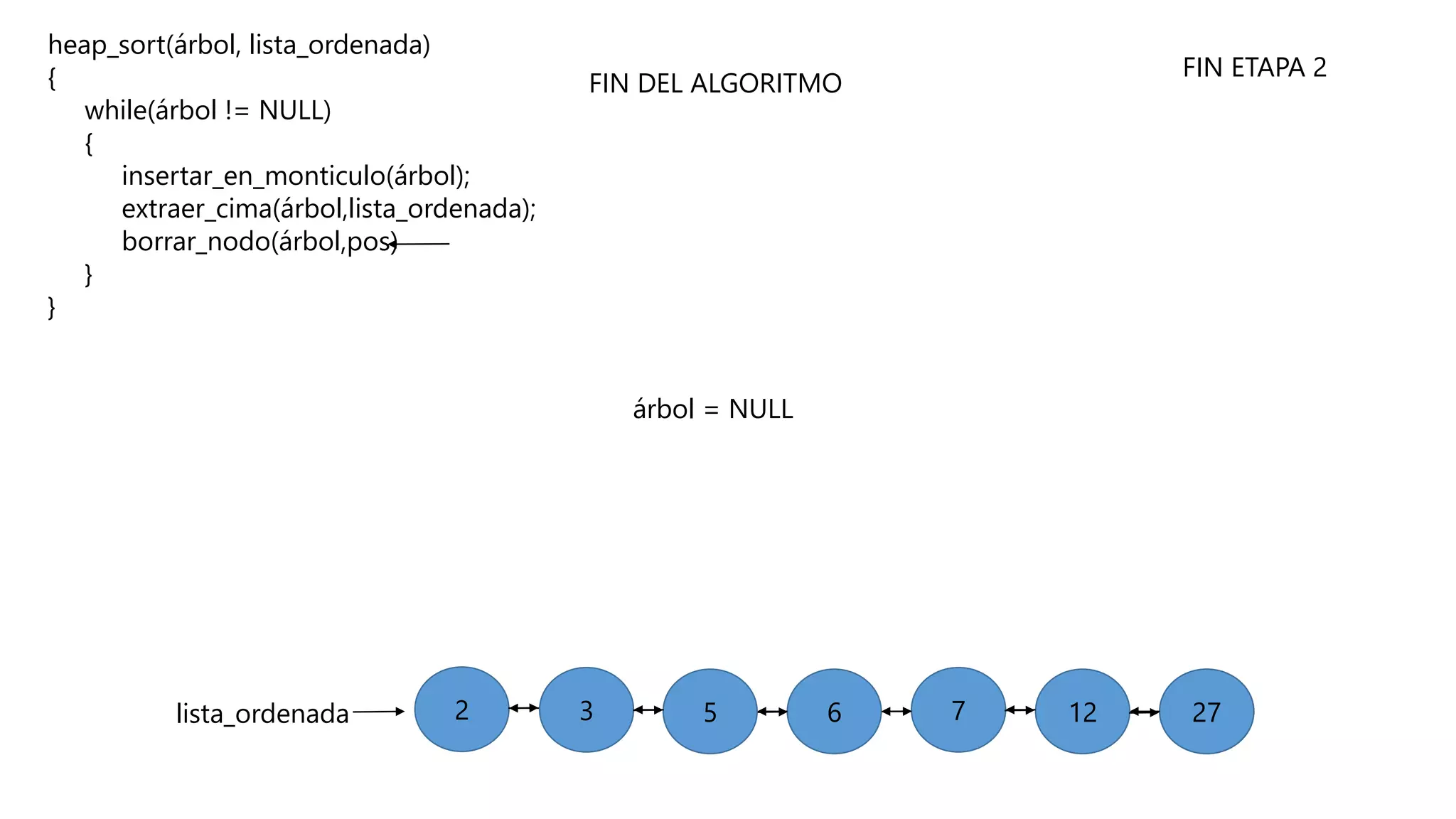
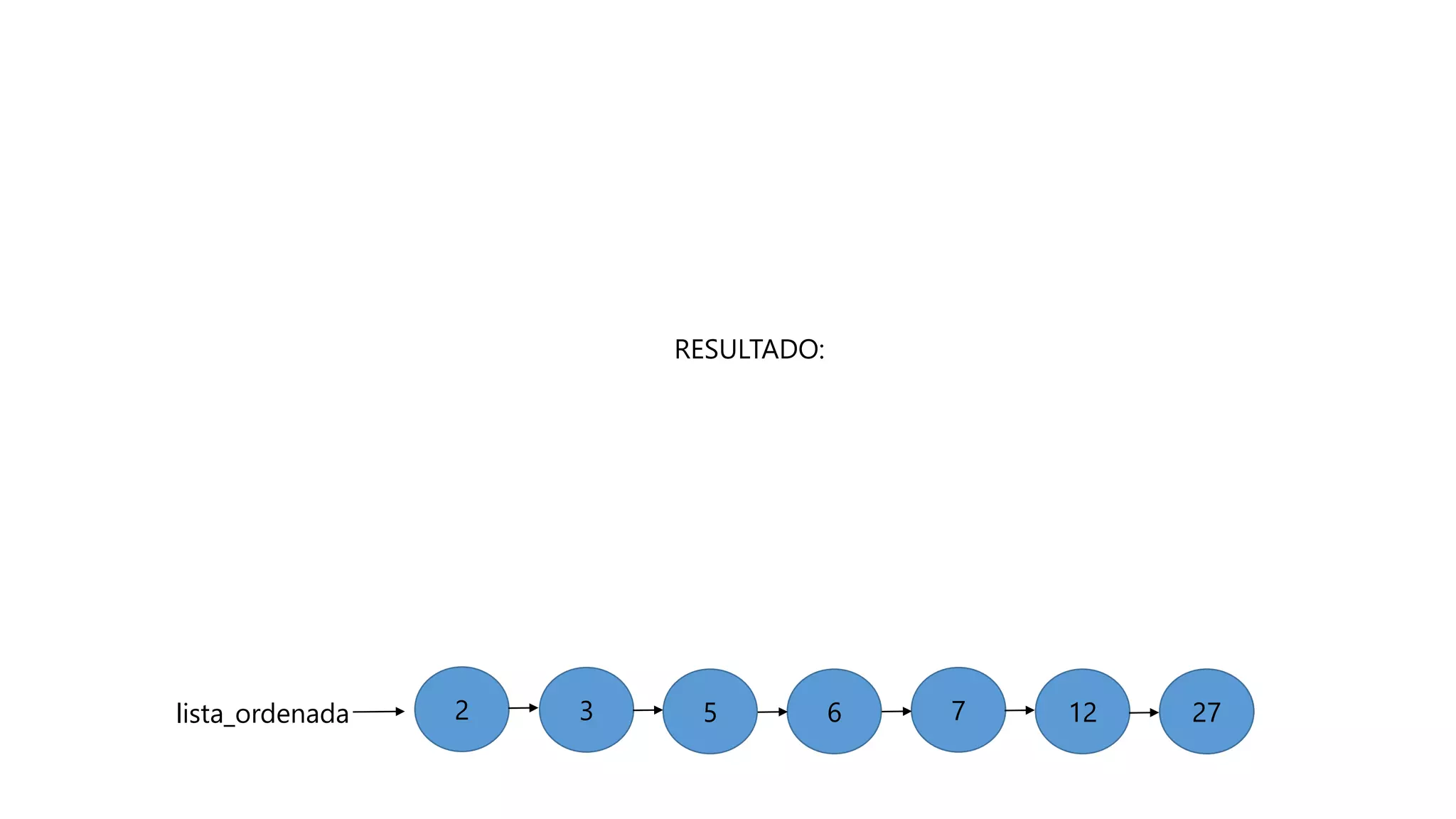
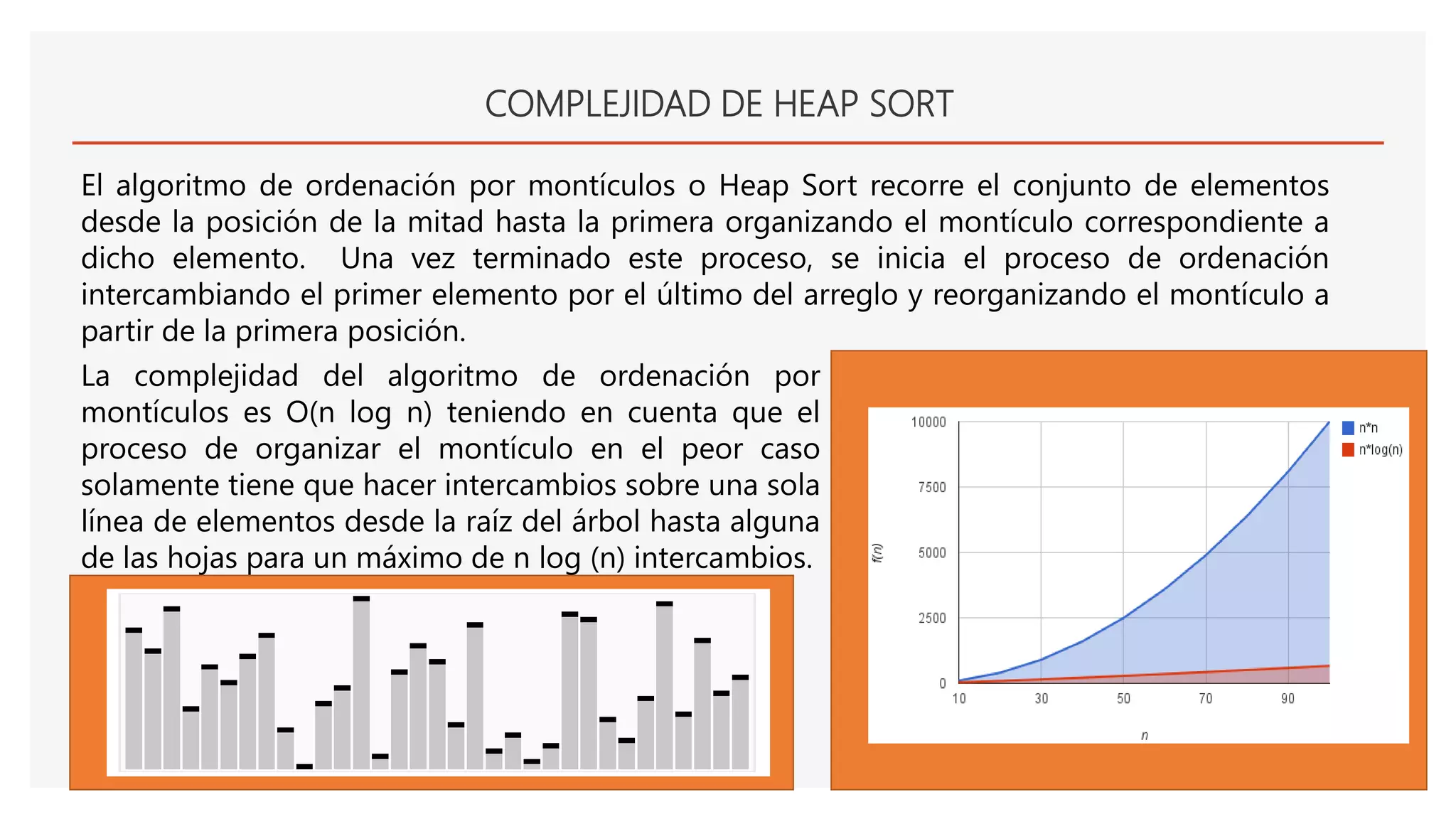
El documento describe el algoritmo de ordenamiento Heap Sort. Este algoritmo ordena los elementos de una lista almacenándolos primero en un montículo y luego extrae el elemento de mayor valor en cada iteración para obtener la lista ordenada. Se explican los pasos del algoritmo y su complejidad computacional asciende a O(n log n) en el peor de los casos.