El documento describe el algoritmo de búsqueda k-vector, el cual permite realizar búsquedas en bases de datos estáticas de forma más eficiente que otros métodos como el binario. El k-vector mapea los valores de la base de datos a una recta de forma que la posición de cada valor en el k-vector indica cuántos valores están por debajo de él en la base de datos, lo que permite identificar de manera rápida qué valores cumplen un criterio de búsqueda dado.



![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-4-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.Pero este m´etodo al ser su formulaci´on general a
cualquier base de datos(est´atica o pseudoest´atica) puede ser
aplicado a una amplia gama de problemas, como:
Interpolaci´on (1D o 2D look-up tables)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-5-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.Pero este m´etodo al ser su formulaci´on general a
cualquier base de datos(est´atica o pseudoest´atica) puede ser
aplicado a una amplia gama de problemas, como:
Interpolaci´on (1D o 2D look-up tables)
B´usqueda de ceros de funciones no-lineales](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-6-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.Pero este m´etodo al ser su formulaci´on general a
cualquier base de datos(est´atica o pseudoest´atica) puede ser
aplicado a una amplia gama de problemas, como:
Interpolaci´on (1D o 2D look-up tables)
B´usqueda de ceros de funciones no-lineales
Inversi´on de funciones no-lineales](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-7-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.Pero este m´etodo al ser su formulaci´on general a
cualquier base de datos(est´atica o pseudoest´atica) puede ser
aplicado a una amplia gama de problemas, como:
Interpolaci´on (1D o 2D look-up tables)
B´usqueda de ceros de funciones no-lineales
Inversi´on de funciones no-lineales
Sampling de distribuciones de probabilidades](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-8-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
El m´etodo de b´usqueda k-vector es un algoritmo que permite
realizar b´usquedas en bases de datos est´aticas, con una mejora
sustancial con respecto a otros m´etodos cl´asicos como el m´etodo
binario,adem´as el costo computacional del mismo es independiente
del tama˜no de la base de datos. Este m´etodo naci´o como una
necesidad en el campo aeroespacial([1]), donde a trav´es del
m´etodo se resuelve con ´exito el problema conocido como
star-tracker.Pero este m´etodo al ser su formulaci´on general a
cualquier base de datos(est´atica o pseudoest´atica) puede ser
aplicado a una amplia gama de problemas, como:
Interpolaci´on (1D o 2D look-up tables)
B´usqueda de ceros de funciones no-lineales
Inversi´on de funciones no-lineales
Sampling de distribuciones de probabilidades](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-9-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Que representa el problema de b´usqueda?
El problema de b´usqueda en un rango de valores de una base de
datos est´atica y(n) con un n´umero de valores n ≫ 1 es encontrar
el subconjunto de elementos que satisfacen y(I), donde I es un
vector de ´ındices tal que y(I) ∈ [ya, yb] donde ya < yb.](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-11-320.jpg)





![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
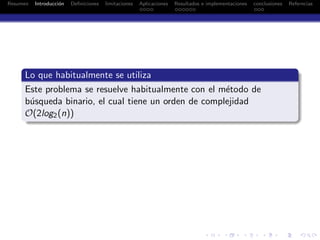
definici´on 1
ymax = m´ax
i
{y(i)} = s(n) (1)
ymin = m´ın
i
{y(i)} = s(1) (2)
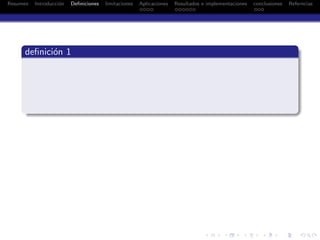
definici´on 2
El coraz´on del algoritmo:
[1, ymin − δǫ] → [n, ymax + δǫ] (3)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-19-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
definici´on 1
ymax = m´ax
i
{y(i)} = s(n) (1)
ymin = m´ın
i
{y(i)} = s(1) (2)
definici´on 2
El coraz´on del algoritmo:
[1, ymin − δǫ] → [n, ymax + δǫ] (3)
Donde:
δǫ = (n − 1)ǫ (4)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-20-320.jpg)










![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Una vez que el k-vector ha sido creado podemos conocer cuantos y
en que posici´on del vector s est´an los datos que buscamos
([ya, yb]). De hecho los ´ındices asociados con estos valores en el
vector s est´an dados por:](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-32-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Una vez que el k-vector ha sido creado podemos conocer cuantos y
en que posici´on del vector s est´an los datos que buscamos
([ya, yb]). De hecho los ´ındices asociados con estos valores en el
vector s est´an dados por:
´ındices de b´usqueda](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-33-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Una vez que el k-vector ha sido creado podemos conocer cuantos y
en que posici´on del vector s est´an los datos que buscamos
([ya, yb]). De hecho los ´ındices asociados con estos valores en el
vector s est´an dados por:
´ındices de b´usqueda
jb = ⌊
ya − q
m
⌋ and jt = ⌈
yb − q
m
⌉ (10)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-34-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Una vez que el k-vector ha sido creado podemos conocer cuantos y
en que posici´on del vector s est´an los datos que buscamos
([ya, yb]). De hecho los ´ındices asociados con estos valores en el
vector s est´an dados por:
´ındices de b´usqueda
jb = ⌊
ya − q
m
⌋ and jt = ⌈
yb − q
m
⌉ (10)
Una vez que tenemos los indices podemos obtener los indices de el
rango de b´usqueda de acuerdo a:](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-35-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Una vez que el k-vector ha sido creado podemos conocer cuantos y
en que posici´on del vector s est´an los datos que buscamos
([ya, yb]). De hecho los ´ındices asociados con estos valores en el
vector s est´an dados por:
´ındices de b´usqueda
jb = ⌊
ya − q
m
⌋ and jt = ⌈
yb − q
m
⌉ (10)
Una vez que tenemos los indices podemos obtener los indices de el
rango de b´usqueda de acuerdo a:
Indices en el k-vector
kstart = k(jb) + 1 and kend = k(jt) (11)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-36-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Elementos buscados
Asi finalmente los elementos buscados en la base de datos y(i) ∈
[ya, yb] son los elementos y(I(k)), donde k ∈ [kstart , kend ]](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-37-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Elementos buscados
Asi finalmente los elementos buscados en la base de datos y(i) ∈
[ya, yb] son los elementos y(I(k)), donde k ∈ [kstart , kend ]Sin
embargo en la base de datos pueden aparecer elementos extra˜nos
originados por el hecho que en promedio los ´ındices kstar y kend
tienen cada uno 50 % de probabilidades de no pertenecer a los
intervalos [ya, z(ja + 1)] y [z(jb, yb)] respectivamente.](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-38-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Elementos buscados
Asi finalmente los elementos buscados en la base de datos y(i) ∈
[ya, yb] son los elementos y(I(k)), donde k ∈ [kstart , kend ]Sin
embargo en la base de datos pueden aparecer elementos extra˜nos
originados por el hecho que en promedio los ´ındices kstar y kend
tienen cada uno 50 % de probabilidades de no pertenecer a los
intervalos [ya, z(ja + 1)] y [z(jb, yb)] respectivamente.Asi si E0 es la
cantidad de elementos esperados en el rango [z(j), z(j + 1)]
entonces el n´umero de elementos extra˜nos esperados en el rango
[ya, yb] es 2E0
2 = E0 = n
(n−1) ≈ 1 para n ≫ 1.](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-39-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Elementos buscados
Asi finalmente los elementos buscados en la base de datos y(i) ∈
[ya, yb] son los elementos y(I(k)), donde k ∈ [kstart , kend ]Sin
embargo en la base de datos pueden aparecer elementos extra˜nos
originados por el hecho que en promedio los ´ındices kstar y kend
tienen cada uno 50 % de probabilidades de no pertenecer a los
intervalos [ya, z(ja + 1)] y [z(jb, yb)] respectivamente.Asi si E0 es la
cantidad de elementos esperados en el rango [z(j), z(j + 1)]
entonces el n´umero de elementos extra˜nos esperados en el rango
[ya, yb] es 2E0
2 = E0 = n
(n−1) ≈ 1 para n ≫ 1. Por ello en presencia
de este elemento extra˜no, debemos hacer dos b´usquedas locales
m´as para eliminar dicho elemento. Formalmente:](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-40-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Elementos buscados
Asi finalmente los elementos buscados en la base de datos y(i) ∈
[ya, yb] son los elementos y(I(k)), donde k ∈ [kstart , kend ]Sin
embargo en la base de datos pueden aparecer elementos extra˜nos
originados por el hecho que en promedio los ´ındices kstar y kend
tienen cada uno 50 % de probabilidades de no pertenecer a los
intervalos [ya, z(ja + 1)] y [z(jb, yb)] respectivamente.Asi si E0 es la
cantidad de elementos esperados en el rango [z(j), z(j + 1)]
entonces el n´umero de elementos extra˜nos esperados en el rango
[ya, yb] es 2E0
2 = E0 = n
(n−1) ≈ 1 para n ≫ 1. Por ello en presencia
de este elemento extra˜no, debemos hacer dos b´usquedas locales
m´as para eliminar dicho elemento. Formalmente:](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-41-320.jpg)








![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Inversi´on de funciones
y(x),x(k)=xmin + (xmax −xmin)(k−1)
(n−1)
s = y(I), s(k + 1) > s(k)
Realizar el k-vector para s
k(1) = 0,k(n) = n
δ = 1
2 max{|y(2 : n) − y(1 : n − 1)|}
Figura: Preprocesamiento
y ∈ [s(1), s(n)], b´usqueda k-vector
X = x(I(K)), Y = y(I(K))
Xs = X(J), Xs(k + 1) > Xs(k)
ji = 1, BUCLE jf = 2 : l
si Xs(jf ) − Xs(jf − 1) > 2∆x
Nroot = Nroot + 1, ne = jf − ji
ne = 1 → k=I(K(J(ji )))
m = min(|Ys(ji : jf − 1)) − y|
Luego alg´un m´etodo para encontrar ra´ıces
Figura: Inversi´on de una funci´on
no-lineal](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-50-320.jpg)





![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Interpolaci´on
Busqueda de datos en una tabla e interpolaci´on
Si consideramos una look-up table discreta de una dimensi´on con
coordenadas x = {x1, x2, x3....xn}T que mapea valores a otro
vector y = {y1, y2, y3....yn}T .La intepolaci´on con k-vector es
primero iniciada construyendo el k-vector fuera del procesamiento
en tiempo real. En este caso el k-vector esta dado por
k = {k1, k2, k3....kn}T donde kj es el n´umero de valores de x que
estan por debajo de la linea que une los puntos [1, −δ] [n, xn + δ]
al j-´esimo indice. Entonces el indice del k-vector es calculado de
acuerdo a:](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-56-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Interpolaci´on
Busqueda de datos en una tabla e interpolaci´on
Si consideramos una look-up table discreta de una dimensi´on con
coordenadas x = {x1, x2, x3....xn}T que mapea valores a otro
vector y = {y1, y2, y3....yn}T .La intepolaci´on con k-vector es
primero iniciada construyendo el k-vector fuera del procesamiento
en tiempo real. En este caso el k-vector esta dado por
k = {k1, k2, k3....kn}T donde kj es el n´umero de valores de x que
estan por debajo de la linea que une los puntos [1, −δ] [n, xn + δ]
al j-´esimo indice. Entonces el indice del k-vector es calculado de
acuerdo a:
j = floor(
x∗ − δ − q
m
) (15)](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-57-320.jpg)
![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Interpolaci´on
Busqueda de datos en una tabla e interpolaci´on
Si consideramos una look-up table discreta de una dimensi´on con
coordenadas x = {x1, x2, x3....xn}T que mapea valores a otro
vector y = {y1, y2, y3....yn}T .La intepolaci´on con k-vector es
primero iniciada construyendo el k-vector fuera del procesamiento
en tiempo real. En este caso el k-vector esta dado por
k = {k1, k2, k3....kn}T donde kj es el n´umero de valores de x que
estan por debajo de la linea que une los puntos [1, −δ] [n, xn + δ]
al j-´esimo indice. Entonces el indice del k-vector es calculado de
acuerdo a:
j = floor(
x∗ − δ − q
m
) (15)
Donde m = xn−x1+2δ
(n−1) . Entonces, para calcular el valor interpolado
y∗, se usa alguno de los m´etodos conocidos de interpolaci´on
(lineal, m´as alto orden, spline, spline c´ubico..) para aproximar entre
xkj
y xkj+1
.](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-58-320.jpg)



![Resumen Introducci´on Definiciones limitaciones Aplicaciones Resultados e implementaciones conclusiones Referncias
Ra´ıces de funciones no-lineales
Implementaci´on preprocesamiento y busqueda de ra´ıces
Como ejemplo de salida t´ıpica de la implementaci´on para la
funci´on y = sinc(x) en [−5, 5] es
octave:3> nonlinear_inversion
Raiz:1 ---> -5
Raiz:2 ---> -4
Raiz:3 ---> -3
Raiz:4 ---> -2
Raiz:5 ---> -1
Raiz:6 ---> 1
Raiz:7 ---> 2
Raiz:8 ---> 3
Raiz:9 ---> 4
Raiz:10 ---> 5
elapsed_time = 0.033457](https://image.slidesharecdn.com/presentacionkvector-140514142907-phpapp01/85/k-vector-search-technique-spanish-62-320.jpg)








