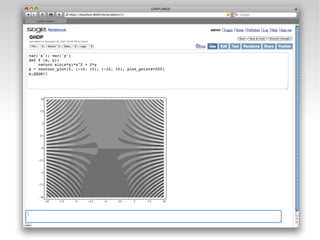
El desarrollo conjunto de Python y R representan probablemente el factor individual más decisivo en el futuro del análisis de datos y el cómputo numérico.

1. Gestión y Análisis de
Datos para las Ciencias
Económicas con
Python y R
Emancipando la Economía
Computacional
Francisco Palm
Spiralia :: SoLVe :: ULA

2. ¿Economía
Computacional?
Intersección entre el Análisis
Económico y la Informática

3. ¿De qué hay que
liberarse?

4. ¿De qué hay que
liberarse?
Herramientas inferiores
Enfoques limitados
Formatos cerrados
Obsolencia planificada
Interoperabilidad reducida

5. "...es probable que el
crecimiento conjunto de
Python y R sea el factor más
importante en el futuro de la
estadística computacional".
"The Future of Statistical Computing"
Leland Wilkinson
(TECHNOMETRICS, Vol. 50, Num. 4, Nov. 2008),

6. ¿Qué es Python?

7. ¿Qué es Python?
➔ Lenguaje dinámico
➔multiparadigma, multipropósito,
multiplataforma,
multiimplementación... multi*
➔ El único compromiso es la
productividad del programador
➔ Viene con las pilas puestas

8. ¿Qué es R?

9. ¿Qué es R?
➔Entorno para computación
estadística y gráficos
➔ Un amplio rango de técnicas y
utilidades (2000+ Paquetes)
➔ Varios años por delante de sus
contrapartes privativas (SAS, SPSS).
➔ Potentes capacidades gráficas

10. ¿En qué se parecen
Python y R?

11. ¿En qué se parecen
Python y R?
 Lenguajes interpretados
 Libres
 "Armas secretas" de Google
 Desarrollados por comunidades
internacionales e independientes
 Amplia difusión internacional
 Modulares y extensibles

12. ¿En qué se diferencian
Python y R?

13. ¿En qué se diferencian?
Python R
 Horizontal,  Vertical, análisis
multipropósito estadístico
 Diseñado para ser  Orientación
sencillo científica
 Técnicas  Funcional, pero
avanzadas de conservador
programación  Hay que instalarlo
 Incluido en Linux (incluso en Linux)

14. Python: numpy
http://numpy.scipy.org/

15. >>> from numpy import *
>>> from numpy.linalg import solve
>>>
>>> # Sistema a resolver para (x0,x1,x2):
>>> # 3 * x0 + 1 * x1 + 5 * x2 = 6
>>> # 1 * x0 + 8 * x2 = 7
>>> # 2 * x0 + 1 * x1 + 4 * x2 = 8
>>>
>>> a = array([[3,1,5],[1,0,8],[2,1,4]])
>>> b = array([6,7,8])
>>> x = solve(a,b)
>>> print x # La solución!
[-3.28571429 9.42857143 1.28571429]
>>>
>>> dot(a,x) # Verificación
array([ 6., 7., 8.])

16. Python: scipy
http://www.scipy.org/

17. from scipy import optimize, special
from numpy import *
from pylab import *
x = arange(0,10,0.01)
for k in arange(0.5,5.5):
y = special.jv(k,x)
plot(x,y)
f = lambda x: -special.jv(k,x)
x_max = optimize.fminbound(f,0,6)
plot([x_max], [special.jv(k,x_max)],'ro')
title(u'Funciones Bessel con optimos locales')
show()

18. Python: Matplotlib
http://matplotlib.sourceforge.net/

19. from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet)
plt.show()

20. Python: persistencia
pickle
marshall
sqlite
zodb
sqlalchemy

21. Python: Django
http://www.djangoproject.com/

22. Python: moin
http://moinmo.in

23. R: Análisis Espacial
http://cran.r-project.org/web/views/Spatial.html

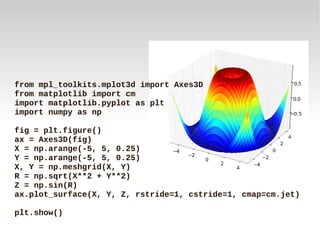
24. library(spatstat)
data(cells)
cells
planar point pattern: 42 points
window: rectangle = [0,1] x [0,1]
plot(cells)
plot(density.ppp(cells))
plot(Kest(cells))

25. R: Econometría y series de
tiempo
http://cran.r-project.org/web/views/Econometrics.html
http://cran.r-project.org/web/views/TimeSeries.html

26. > mort = ts(scan("cmort.dat"),start=1970, frequency=52)
Read 508 items
> part = ts(scan("part.dat"),start=1970, frequency=52)
Read 508 items
> ded = ts.intersect(mort,part,part4=lag(part,-4),dframe=TRUE)
> fit = lm(mort~part+part4, data=ded, na.action=NULL)
> summary(fit)
Call:
lm(formula = mort ~ part + part4, data = ded, na.action = NULL)
Residuals:
Min 1Q Median 3Q Max
-22.7429 -5.3677 -0.4136 5.2694 37.8539
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 69.01020 1.37498 50.190 < 2e-16 ***
part 0.15140 0.02898 5.225 2.56e-07 ***
part4 0.26297 0.02899 9.071 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.323 on 501 degrees of freedom
Multiple R-squared: 0.3091, Adjusted R-squared: 0.3063
F-statistic: 112.1 on 2 and 501 DF, p-value: < 2.2e-16

27. R: Finanzas
http://cran.r-project.org/web/views/Finance.html

28. R: Optimización
http://cran.r-project.org/web/views/Optimization.html

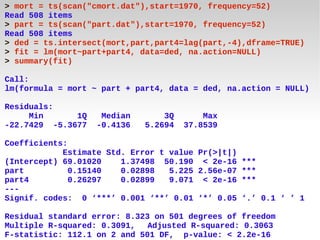
29. # Formular el problema: maximizar
# x1 + 9 x2 + x3 sujeto a
# x1 + 2 x2 + 3 x3 <= 9
# 3 x1 + 2 x2 + 2 x3 <= 15
#
f.obj <- c(1, 9, 3)
f.con <- matrix (c(1, 2, 3, 3, 2, 2), nrow=2, byrow=TRUE)
f.dir <- c("<=", "<=")
f.rhs <- c(9, 15)
#
# Ejecutar.
#
lp ("max", f.obj, f.con, f.dir, f.rhs)
## Salida: Exito: la funcion objetivo es 40.5
lp ("max", f.obj, f.con, f.dir, f.rhs)$solution
## Salida: [1] 0.0 4.5 0.0
#
# Obtener variables duales
lp ("max", f.obj, f.con, f.dir, f.rhs, compute.sens=TRUE)$duals
## Salida: [1] 4.5 0.0 -3.5 0.0 -10.5

30. R: rattle
http://rattle.togaware.com/

31. R: persistencia
read.table, write.table
DBI, filehash, filehashsqlite,
RMySQL, RODBC, ROracle,
RPostgreSQL
TSSQLite, TSMySQL, TSodbc,
TSPostgreSQL ...

32. Python & R: Sage
http://www.sagemath.org/

34. Python & R: manageR
http://www.ftools.ca/manageR/

35. Notas Finales
Komodo Edit – Sciviews-K
http://www.sciviews.org/SciViews-K/index.html

36. Contacto
francisco.palm@gmail.com
fpalm@ula.ve