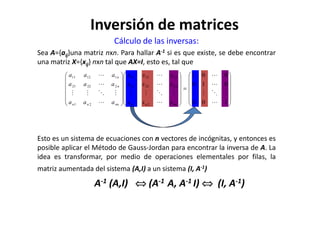
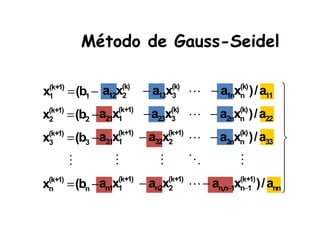
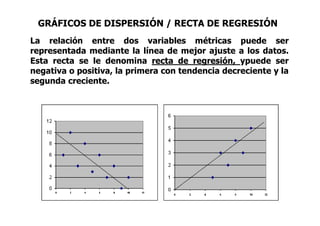
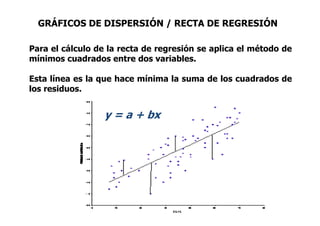
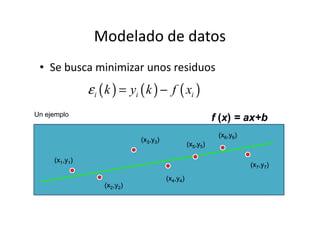
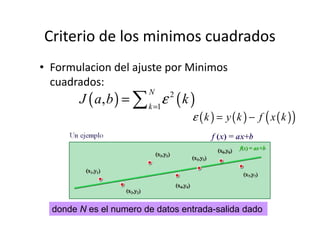
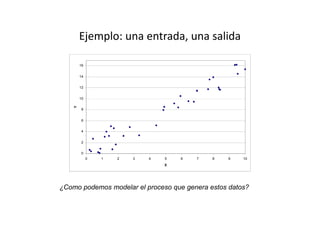
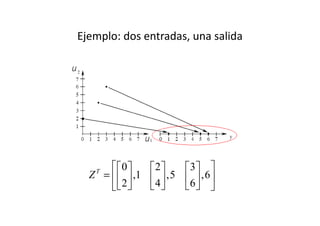
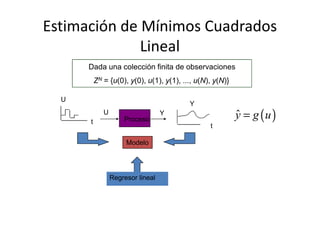
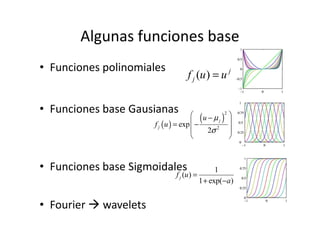
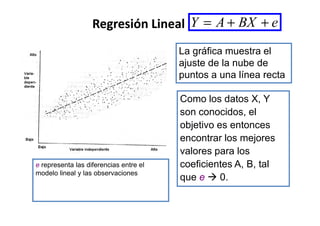
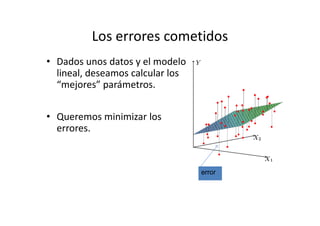
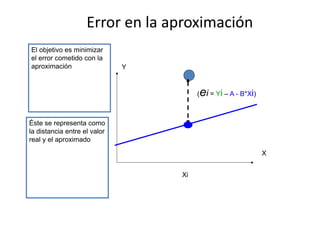
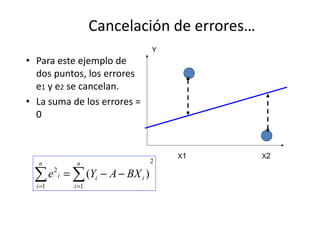
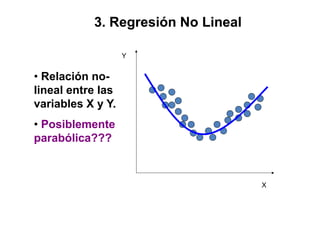
Este documento describe diferentes métodos matemáticos como la inversión de matrices, sistemas de ecuaciones lineales y mínimos cuadrados. Explica cómo calcular la inversa de una matriz y las propiedades de la inversión matricial. También cubre métodos para resolver sistemas de ecuaciones lineales como los métodos de Jacobi y Gauss-Seidel. Finalmente, introduce el concepto de ajuste de curvas por mínimos cuadrados para modelar datos experimentales.

1. Algoritmos matemáticos para:
sistemas de ecuaciones lineales,sistemas de ecuaciones lineales,
inversión de matrices y mínimos
cuadrados
Jose Aguilar

2. Inversión de matrices
Definición (Inversa de una matriz): Sea A una matriz nxn. Una matriz C de nxn
es una inversa de A si CA=AC=I.
Para la matriz no es difícil verificar que la matriz
satisface que






−
−
=
21
94
A 





=
41
92
C






=





−
−






10
01
21
94
41
92
Se dice entonces que la matriz C es una inversa de la matriz A. Esto se define
enseguida:
Teorema: Sea A una matriz nxn con inversa C tal que CA=AC=I. Si D es otra
matriz nxn tal que AD=I, entonces C=D.
Demostración: Como la multiplicación de matrices es asociativa, se tiene que
C(AD)=(CA)D, de donde, como AD=I y CA=I, se tiene que
C(AD)=CI=C y (CA)D=ID=D, por tanto, C=D.

3. Se denotará la inversa de una matriz A, cuando exista, como A-1. Entonces A
A-1 = A-1 A = I. Nótese que no se debe expresar A-1 como 1/A.
Definición: Una matriz cuadrada que tiene inversa se llama invertible. Una
matriz cuadrada que no tiene inversa se llama singular.
Teorema: La matriz 





=
dc
ba
A
Inversión de matrices
es invertible si ad - bc ≠0, en cuyo caso la inversa está dada por la fórmula
Teorema: Sean A y B matrices invertibles nxn. Entonces:
a) AB es invertible
b) (AB)-1 = B-1 A-1



 dc










−−
−
−
−=





−
−
−
=−
bcad
a
bcad
c
bcad
b
bcad
d
ac
bd
bcad
A
11

4. inversión de matrices
Propiedades de la inversión de matrices
La matriz inversa, si existe, es única
A-1·A = A·A-1= I
(At) –1 = (A-1) t
(A·B)-1 = B-1·A-1
(A-1)-1 = A
(kA)-1 = (1/k) · A-1

5. inversión de matrices
Observación:
Podemos encontrar matrices que cumplen A·B = I, pero que B·A ≠ I, en tal
caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la
inversa de A "por la derecha".
Por el método de Gauss-Jordan
Usando determinantes
Directamente
Hay varios métodos para calcular la matriz inversa de una matriz
dada:

6. inversión de matrices
Dada la matriz buscamos una matriz que cumpla A·A-1 = I, es decir
Cálculo Directo de la Matriz Inversa
La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil
comprobar que también cumple A-1 · A = I, con lo cual es realmente la inversa de A.
Para ello planteamos el sistema de ecuaciones:

7. Cálculo de las inversas:
Sea A={aij}una matriz nxn. Para hallar A-1 si es que existe, se debe encontrar
una matriz X={xij} nxn tal que AX=I, esto es, tal que














=




























100
010
001
21
22221
11211
21
22221
11211
⋯
⋮⋱⋮⋮
⋯
⋯
⋯
⋮⋱⋮⋮
⋯
⋯
⋯
⋮⋱⋮⋮
⋯
⋯
nnnn
n
n
nnnn
n
n
xxx
xxx
xxx
aaa
aaa
aaa
Inversión de matrices
Esto es un sistema de ecuaciones con n vectores de incógnitas, y entonces es
posible aplicar el Método de Gauss-Jordan para encontrar la inversa de A. La
idea es transformar, por medio de operaciones elementales por filas, la
matriz aumentada del sistema (A,I) a un sistema (I, A-1)
A-1 (A,I) ⇔⇔⇔⇔ (A-1 A, A-1 I) ⇔⇔⇔⇔ (I, A-1)

8. Sistema de ecuaciones lineales
a11x1+a12x2+...+a1nxn=b1
.
.
.
an1x1+an2x2+...+annxn=bn

9. SISTEMA DE ECUACIONESSISTEMA DE ECUACIONES
LINEALESLINEALES
sistema de ecuaciones lineales, por ejemplo 2x1 - 3x2=7
3x1 - x2=2,
tiene asociado una matriz A correspondiente a las incógnitas, y un vector b
correspondiente a los términos independientes, es decir,






=
2
7
b






−
−
=
13
32
A
Si ahora se escriben las incógnitas como un vector
se puede denotar el sistema de ecuaciones lineales
como Ax=b, es decir
Esta última ecuación sugiere la noción de multiplicación de una matriz A por
un vector columna x.



2


 −
=
13
A






=
2
1
x
x
x






=











−
−
2
7
13
32
2
1
x
x

10. Métodos directos e iterativosMétodos directos e iterativos
DIRECTOSDIRECTOS
• Ax =b
ITERATIVOSITERATIVOS
• x = Cx + d• Ax =b
• x = A-1 b
• Tamaño pequeño
• x(k+1) = Cx(k) + d
• Tamaño grande
x=A-1b
Limx->∞=Cx+d

11. Sistema de ecuaciones lineales
2x1+3x2=2
x1+x2=3
x2=2/3-(2/3)x1
x2=3-x1
3-x1=2/3-(2/3)x1 3-2/3 =x1-(2/3)x1
2.333=0.333x1 x1=7

12. Método de JacobiMétodo de Jacobi
A L D U
x D (b (L U)x )(k 1) 1 (k)
= + +
= − ++ −
- U=triang. sup; L=triang. Inf.
- D=diag(A);
La ecuación A x = b se transforma en (D - L - U) x = b
x = (L + U) x + b

13. Algoritmo Método de JacobiAlgoritmo Método de Jacobi
función Jacobi (A,)
// x0 es una aproximación inicial a la solución//
K=0
Mientras no convergencia
para i=1 hasta npara i=1 hasta n
y=0
para j=1 hasta n
si j≠i entonces
y=y+aij xj
k
xi
k+1= (bi-y)/aii
K=K+1

14. Método de Gauss-SeidelMétodo de Gauss-Seidel
x (b
x (b
a x a x a x )/a
a x a x a x )/a
1
(k+1)
1
(k+1)
12 2
(k)
13 3
(k)
1n n
(k)
11
(k+1) (k) (k)
= −
= −
− −
− −


⋯
⋯ x (b
x (b
x (b
a x a x a x )/a
a x a x a x )/a
a x a x a x )/a
2
(k+1)
2
3
(k+1)
3
n
(k+1)
n
21 1
(k+1)
23 3
(k)
2n n
(k)
22
31 1
(k+1)
32 2
(k+1)
3n n
(k)
33
n1 1
(k+1)
n2 2
(k+1)
n,n 1 n 1
(k+1)
nn
= −
= −
= −
− −
− −
− −

− −
⋮
⋯
⋯
⋮ ⋮ ⋱ ⋮
⋯







15. Modelo matricialModelo matricial
A L D U
(L D)x b Ux
x (L D) (b Ux )
(k 1) (k)
(k 1) 1 (k)
= + +
+ = −
= + −
+
+ −
- D = diag(A)
- U=triang. Sup; L=triang inf

16. Algoritmo Método de Gauss-SeidelAlgoritmo Método de Gauss-Seidel
función Gaussi (A, x, b)
// x0 es una aproximación inicial a la solución//
para k=1 hasta convergencia
para i=1 hasta npara i=1 hasta n
y=0
para j=1 hasta n
si j≠i entonces
y=y+aij xj
xi= (bi-y)/aii

17. APROXIMACIÓN DE MÍNIMOSAPROXIMACIÓN DE MÍNIMOS
CUADRADOS

18. Modelado de datos
• El modelado de datos se puede expresar de la
siguiente forma:
• Dadas:
(x , y )
– Una colección finita de datos
– Una forma funcional
• Hallar los parámetros de la función
– que mejor representen la relación entre los datos
(xi, yi)
y = f (x)

19. Para comprender datos experimentales, deseamos
determinar una recta o una curva que “encaje” o “se ajuste”
más (o describa mejor) estos datos
Imaginemos la siguiente tabla con los pasados de un curso
en semestres pasados.
Curso 1 2 3 4 5 6
Ejemplo
Si quisiéramos trazar una recta que acerque a los puntos en la
tabla hay muchas opciones. Sin embargo, hay una que se ajusta
mejor a estos datos, bajo cierto criterio.
Caso anterior es y = 0.13333 + 0.05 x
Curso
Porcentaje
de pasados
1
0.70 0.75 0.80 0.80 0.85 0.80
2 3 4 5 6

20. La relación entre dos variables métricas puede ser
representada mediante la línea de mejor ajuste a los datos.
Esta recta se le denomina rectarecta dede regresión,regresión, ypuede ser
negativa o positiva, la primera con tendencia decreciente y la
segunda creciente.
GRÁFICOS DE DISPERSIÓN / RECTA DE REGRESIÓN

21. Para el cálculo de la recta de regresión se aplica el método de
mínimos cuadrados entre dos variables.
Esta línea es la que hace mínima la suma de los cuadrados de
los residuos.
GRÁFICOS DE DISPERSIÓN / RECTA DE REGRESIÓN
y = a + bxy = a + bx

22. Modelado de datos
• Se busca minimizar unos residuos
( ) ( ) ( )i i ik y k f xε = −
f (x) = ax+bUn ejemplo
(x(x11,y,y11))
(x(x22,y,y22))
(x(x33,y,y33))
(x(x44,y,y44))
(x(x55,y,y55))
(x(x66,y,y66))
(x(x77,y,y77))
f (x) = ax+bUn ejemplo

23. Criterio de los minimos cuadrados
• Formulacion del ajuste por Minimos
cuadrados:
( ) ( )2
1
,
N
k
J a b kε=
= ∑
( ) ( ) ( )( )k y k f x kε = −
donde N es el numero de datos entrada-salida dado
( ) ( ) ( )( )k y k f x kε = −

24. Llamemos a “u” perturbación o error, siendo la diferencia que hay entre el
valor observado de la variable exógena (y) y el valor estimado que
obtendremos a través de la recta de regresión .
La metodología para la obtención de la recta será hacer MÍNIMA la suma de
los CUADRADOS de las perturbaciones. ¿Por qué se elevan al cuadrado?
ˆiy
ii bxay +=
∧
los CUADRADOS de las perturbaciones. ¿Por qué se elevan al cuadrado?
2 2
ˆ( )i i iu y y= −
2 2
1 1
ˆ( )
n n
i i i
i i
u y y
= =
= −∑ ∑
( )
22 2
, 1 1 1
ˆ( )min
n n n
i i i i i
q p i i i
xpu qy y y
= = =
 
= − = − +   
 
∑ ∑ ∑ a b

25. Un problema de optimizacion
• Aproximaciones computacionales:
– Algoritmos numéricos generales para la minimización de
una función
• Basados en el gradiente; algoritmos numéricos generales para• Basados en el gradiente; algoritmos numéricos generales para
hallar raíces; algoritmos que aprovechan la forma de la función
– Algoritmos con una aproximación basada en la inteligencia
artificial: algoritmos genéticos
• Solución analítica: mínimos cuadrados lineal

26. La aproximacion de funciones
• Al realizar la aproximacion de una funcion,
sólo están disponibles un número finito de
muestras
( ) ( )( ) ( ) ( )( ) ( ) ( )( ){ }ˆ ˆ ˆ1 , 1 , , , , ,N
Z u y u k y k u N y N= ⋯ ⋯

27. Ejemplo: una entrada, una salida
8
10
12
14
16
Y
0
2
4
6
0 1 2 3 4 5 6 7 8 9 10
X
¿Como podemos modelar el proceso que genera estos datos?

28. Ejemplo: dos entradas, una salida
0 2 3
,1 ,5 ,6
2 4 6
T
Z
      
=       
      

29. Modelos lineales vs . No lineales
• Es común asumir que f (u) pertenece a una
familia de funciones que comparten la misma
estructura y difieren por los valores tomados
por ciertos parámetros θ.por ciertos parámetros θ.
( ),y f u θ=

30. El modelo lineal
• Un modelo lineal asume que la función es
lineal respecto a los parámetros θ
( ) ( ) ( ) ( ),f u f u f u f uθ θ θ θ= + + +⋯( ) ( ) ( ) ( )1 1 2 2, q qf u f u f u f uθ θ θ θ= + + +⋯
Aquí, la linealidad se refiera a “con
respecto a los parametros”

31. Modelos no-lineales
• En los modelos no-lineales la función es no-
lineal respecto a los paramétros θ
( ) ( ), expf u uθ θ= −( ) ( ), expf u uθ θ= −

32. Estimación de Mínimos Cuadrados
Lineal
Dada una colección finita de observaciones
ZN = {u(0), y(0), u(1), y(1), ..., u(N), y(N)}
YU
U
Y
( )ˆy g u=t
t
YU
Proceso
Modelo
Regresor lineal
( )ˆy g u=

33. • El método de regresión de mínimos cuadrados
consiste en encontrar la curva o función que mejor se
ajuste a una serie de puntos (Xi,Yi), obtenidos
generalmente a partir de un experimento.
• La estrategia consiste en minimizar las diferencias
Mínimos Cuadrados
• La estrategia consiste en minimizar las diferencias
entre la función y los datos observados.
• El caso o ejemplo más sencillo es el ajuste de una
función lineal a la serie de puntos.

34. Regresión lineal
Se asume que la relación entrada-salida puede ser
descrita por una estructura de regresor lineal
f(u,θ) es denominada la funcion de ajuste. Las fi(u) son
denominadas las funciones base
( ) ( ) ( ) ( )1 1 2 2, q qf u f u f u f uθ θ θ θ ε= + + + +⋯

35. Algunas funciones base
• Funciones polinomiales
• Funciones base Gausianas
( ) j
jf u u=
( )
2
µ −
• Funciones base Gausianas
• Funciones base Sigmoidales
• Fourier wavelets
( )
( )
2
2
exp
2
j
j
u
f u
µ
σ
 −
 = −
 
 
1
( )
1 exp( )
jf u
a
=
+ −

36. RegresiónRegresión LinealLineal
La gráfica muestra el
ajuste de la nube de
puntos a una línea recta
eBXAY ++=
Como los datos X, Y
son conocidos, elson conocidos, el
objetivo es entonces
encontrar los mejores
valores para los
coeficientes A, B, tal
que e 0.
e representa las diferencias entre el
modelo lineal y las observaciones

37. Los errores cometidos
• Dados unos datos y el modelo
lineal, deseamos calcular los
“mejores” parámetros.
• Queremos minimizar los• Queremos minimizar los
errores.
error

38. Error en la aproximación
Y
(ei = Yi – A - B*Xi)
El objetivo es minimizar
el error cometido con la
aproximación
X
Xi
Éste se representa como
la distancia entre el valor
real y el aproximado

39. Los residuos
• El ajuste de minimos cuadrados halla el vector
de parametros θ tal que se minimiza
( )21 N
J kε= ∑
( ) ( ) ( )( )ˆ ,k y k f u kε θ= −
( )2
1
1 N
k
J k
N
ε=
= ∑
residuos = errores

40. Criterio para el mejor ajuste
• Como se tiene una serie de n puntos (Xi, Yi)
(i=1,…,n), la acumulación de los errores será:
∑∑ −−=
n
ii
n
i BXAYe )(
• Para que los valores de error positivos y negativos
no se cancelen entre sí, éstos se deben elevar al
cuadrado
∑∑ ==
−−=
i
ii
i
i BXAYe
11
)(

41. Cancelación de errores…
• Para este ejemplo de
dos puntos, los errores
e1 y e2 se cancelan.
• La suma de los errores =
0
Y
0
X1 X2
2
11
2
)(∑∑ ==
−−=
n
i
ii
n
i
i BXAYe

42. ∑∑ ==
−−==
n
i
ii
n
i
i BXAYeS
1
2
1
2
)(
Regresión LinealRegresión Lineal
• Sea:
• Como el objetivo es encontrar A y B, tal que S
sea mínimo, para esto se deriva S
parcialmente con respecto a A y B
respectivamente y se igualan a cero

43. Sistema de ecuaciones para encontrar A y B
• Las derivadas parciales de S con respecto a A y
a B se hacen cero, así:
∑ =−−−=
∂
0)1)((2 BXAY
S (1)
∑ =−−−=
∂
∂
∑ =−−−=
∂
∂
0))((2
0)1)((2
XBXAY
B
S
BXAY
A
S (1)
(2)

44. En resumen las fórmulas para calcular los coeficientes A y B de una
función lineal de regresión con sólo dos tipos de variables X y Y son:
Regresión LinealRegresión Lineal -- FórmulasFórmulas
∑ −−
N
YYXX ))((
XBYA −=
∑ ∑
∑
∑
= =
=
=
==
−
−−
=
N
i
N
i
iiN
i
i
i
ii
Y
N
YX
N
X
XX
YYXX
B
1 1
1
2
1 1
;
1
;
)(
))((

45. Regresión LinealRegresión Lineal -- AlgoritmoAlgoritmo
Entrada: Número de datos n, datos (x,y)
sumx, sumy, sumxy, sumx2 = 0
i=0
Mientras i<=n-1
sumx=sumx+x(i)sumx=sumx+x(i)
sumy=sumy+y(i)
sumx2=sumx2+(x(i)*x(i))
sumxy=sumxy+(x(i)*y(i))
i=i+1
Denominador=sumx*sumy-n*sumx2
a=(sumx*sumy-n*sumxy)/Denominador
b=(sumx*sumxy-sumx2*sumy)/Denominador
Imprimir a y b

46. :
:
AeYlExponencia
AXYPotencia
BX
B
=
=
Regresión No LinealRegresión No Lineal
Hay ocasiones en las cuales la relación existente entre X y Y no es lineal, sin
embargo ésta puede ser descrita por algún otro tipo de función. EJ:
2
2
210
:
...:
)()(
)()();(:
:
CXBXAYParabólica
XAXAXAAYPolinómica
ALogBXYLog
ALogXBLogYXBLogAYaLogarítmic
AeYlExponencia
N
N
ee
BX
++=
++++=
+=
+=+=
=

47. • Relación no-
lineal entre las
variables X y Y.
3. Regresión No Lineal3. Regresión No Lineal
Y
• Posiblemente
parabólica???
X

48. RegresiónRegresión nono--lineal:lineal: PotenciaPotencia:
B
AXY =
( )
N
XLog
XLog
N
YLogXLog
YLogXLog
B
N
i
iN
i
i
N
i
N
i
i
N
i
i
ii
2
1
1
2
1
11
)(
)(
)()(
)(*)(




∑
−∑
∑




∑



∑
−
=
=
=
=
==
;;
Ni
i
1
∑
=









 ∑
−
∑
= ==
N
XLog
B
N
YLog
A
N
i
i
N
i
i
11
)()(
exp

49. RegresiónRegresión nono--lineal:lineal: ExponencialExponencial:
BX
AeY =
( )
2
11
2
111
1
)(
1
)(




∑−∑




∑



∑−∑
=
==
===
N
i
i
N
i
i
N
i
i
N
i
i
N
i
ii
X
N
X
YLogX
N
YLogX
B ;;









 ∑
−
∑
= ==
N
X
B
N
YLog
A
N
i
i
N
i
i
11
)(
exp