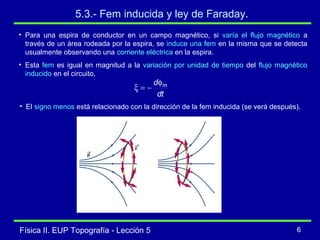
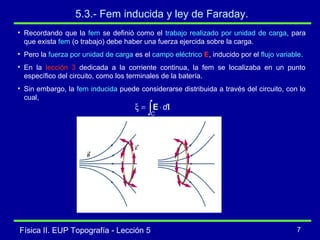
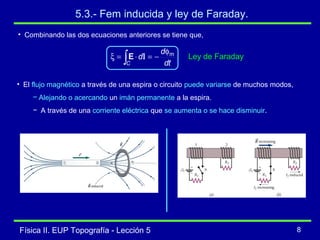
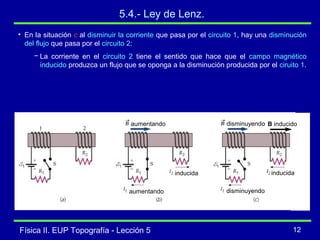
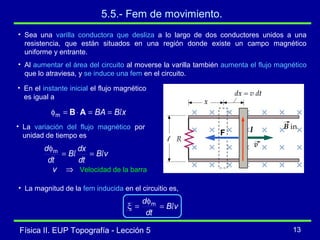
La lección describe la inducción magnética, incluyendo que una variación en el flujo magnético a través de un circuito induce una fuerza electromotriz (fem) de acuerdo con la ley de Faraday. Explica conceptos como el flujo magnético, la fem inducida, y la ley de Lenz, la cual establece que la corriente inducida se orienta para oponerse al cambio que la produce. También cubre la fem inducida por el movimiento de un conductor a través de un campo magnético.

1. Física II. EUP Topografía - Lección 5 1
Lección 5.- Inducción
Magnética
Física II – E.U.P. Topografía

2. Física II. EUP Topografía - Lección 5 2
Lección 5.- Inducción Magnética
5.1.- Introducción.
5.2.- Flujo magnético.
5.3.- Fem inducida y ley de Faraday.
5.4.- Ley de lenz.
5.5.- Fem de movimiento.
5.6.- Inductancia.

3. Física II. EUP Topografía - Lección 5 3
5.1.- Introducción.
 En la década de 1830, Michael Faraday y Joseph Henry descubrieron que un campo
magnético induce una corriente en un conductor, siempre que el campo sea variable.
 Las fuerzas electromotrices y corrientes eléctricas causadas por campos magnéticos
variables se denominan fems inducidas y corrientes inducidas, y al fenómeno en sí se
llama inducción magnética.
 Los campos magnéticos variables pueden
obtenerse de distintos modos:
• Mediante imanes móviles.
• A través de corrientes variables.
• Al alejar o acercar la bovina del conductor
o imán.
• Al hacer girar la bovina en un campo
magnético fijo (generador).
 Todos estos métodos se pueden recoger mediante una expresión conocida como ley de
Faraday, que relaciona el cambio del flujo magnético a través de un circuito con la fem
inducida en el circuito.

4. Física II. EUP Topografía - Lección 5 4
5.2.- Flujo magnético.
• Sea dA un vector que representa a un área elemental de una superficie A, situada en
una región donde está presente un campo magnético B.
• El flujo magnético a través de A se define por la expresión
• La unidad de φm en el SI es el weber (Wb).
2
mT1Wb1 ⋅=
• Como B es proporcional al número de líneas de campo por unidad de área, φm es
proporcional al número de líneas de campo que atraviesan el área.
∫∫∫ =θ=⋅=φ
SSS
dABBdAd nm cosAB
⇒θ= cosn BB Componente de B según la
dirección normal a dA
dA
A

5. Física II. EUP Topografía - Lección 5 5
5.2.- Flujo magnético.
• Es frecuente tratar con una bovina de alambre que contiene N vueltas.
• En este caso el flujo a través de la bovina es igual al producto de N por el flujo que
atraviesa una sola vuelta,
• Si la superficie es un plano de área A y B es constante en magnitud y dirección, y forma
un ángulo θ con el vector que representa a esa área, el flujo es
(Área dentro de
una espira)
θ=φ cosm BA
θ=φ cosm NBA

6. Física II. EUP Topografía - Lección 5 6
5.3.- Fem inducida y ley de Faraday.
• Para una espira de conductor en un campo magnético, si varía el flujo magnético a
través de un área rodeada por la espira, se induce una fem en la misma que se detecta
usualmente observando una corriente eléctrica en la espira.
• Esta fem es igual en magnitud a la variación por unidad de tiempo del flujo magnético
inducido en el circuito,
dt
d mφ
−=ξ
• El signo menos está relacionado con la dirección de la fem inducida (se verá después).

7. Física II. EUP Topografía - Lección 5 7
5.3.- Fem inducida y ley de Faraday.
• Recordando que la fem se definió como el trabajo realizado por unidad de carga, para
que exista fem (o trabajo) debe haber una fuerza ejercida sobre la carga.
• Pero la fuerza por unidad de carga es el campo eléctrico E, inducido por el flujo variable.
• En la lección 3 dedicada a la corriente continua, la fem se localizaba en un punto
específico del circuito, como los terminales de la batería.
• Sin embargo, la fem inducida puede considerarse distribuida a través del circuito, con lo
cual,
∫ ⋅=ξ
C
dlE

8. Física II. EUP Topografía - Lección 5 8
5.3.- Fem inducida y ley de Faraday.
• Combinando las dos ecuaciones anteriores se tiene que,
dt
d
d
C
mφ
−=⋅=ξ ∫ lE Ley de Faraday
• El flujo magnético a través de una espira o circuito puede variarse de muchos modos,
− Alejando o acercando un imán permanente a la espira.
− A través de una corriente eléctrica que se aumenta o se hace disminuir.

9. Física II. EUP Topografía - Lección 5 9
5.3.- Fem inducida y ley de Faraday.
− La propia espira puede alejarse o acercarse a la fuente de flujo.
− El área de la espira puede aumentar o disminuir en el interior de un campo B fijo.

10. Física II. EUP Topografía - Lección 5 10
5.4.- Ley de Lenz.
• El signo negativo de la ley de Faraday está relacionado con la dirección y sentido de la
fem y corriente inducidas.
• Estos pueden determinarse a partir de la ley de Lenz, que dice:
− La fem y la corriente inducidas tienen una dirección y sentido tal que tienden a
oponerse a la variación que las produce.
• En esta figura el movimiento del imán hacia la espira aumenta el flujo que pasa por ella.
• La corriente inducida en la espira produce un campo magnético propio.
• El sentido de esta corriente es aquel que produce un flujo magnético que se opone al del
imán. El campo magnético inducido tiende a disminuir el flujo que atraviesa la espira.
inducido

11. Física II. EUP Topografía - Lección 5 11
5.4.- Ley de Lenz.
• En esta figura cuando se hace variar la corriente en el circuito 1, hay un cambio en el
flujo que atraviesa el circuito 2.
• En la situación b al aumentar la corriente que pasa por el circuito 1, hay un aumento del
flujo que pasa por el circuito 2:
− La corriente en el circuito 2 tiene el sentido que hace que el campo magnético
inducido produzca un flujo que se oponga al aumento producido por el ciruito 1.
inducida inducida
aumentando
aumentando disminuyendo
disminuyendo
B inducido

12. Física II. EUP Topografía - Lección 5 12
5.4.- Ley de Lenz.
• En la situación c al disminuir la corriente que pasa por el circuito 1, hay una disminución
del flujo que pasa por el circuito 2:
− La corriente en el circuito 2 tiene el sentido que hace que el campo magnético
inducido produzca un flujo que se oponga a la disminución producida por el ciruito 1.
inducida
aumentando
aumentando disminuyendo
disminuyendo
B inducido
inducida

13. Física II. EUP Topografía - Lección 5 13
5.5.- Fem de movimiento.
• Sea una varilla conductora que desliza a lo largo de dos conductores unidos a una
resistencia, que están situados en una región donde existe un campo magnético
uniforme y entrante.
• Al aumentar el área del circuito al moverse la varilla también aumenta el flujo magnético
que lo atraviesa, y se induce una fem en el circuito.
• En el instante inicial el flujo magnético
es igual a
xBBA l==⋅=φ ABm
• La variación del flujo magnético por
unidad de tiempo es
vB
dt
dx
B
dt
d
ll ==
φm
⇒v Velocidad de la barra
• La magnitud de la fem inducida en el circuitio es,
vB
dt
d
l=
φ
=ξ m
IF