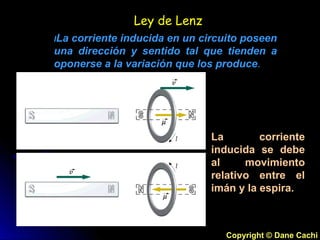
Este documento describe los principios de la inducción magnética y la corriente alterna. 1) Michael Faraday y Joseph Henry descubrieron de forma independiente que un campo magnético variable induce una corriente eléctrica en un conductor cercano. 2) La ley de Faraday establece que la fuerza electromotriz inducida en un circuito es proporcional al cambio en el flujo magnético a través del circuito. 3) Un generador de corriente alterna utiliza una bobina giratoria en un campo magnético para producir una corriente eléctrica