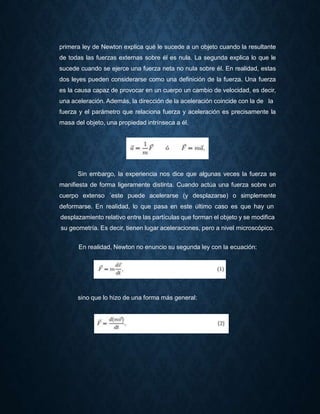
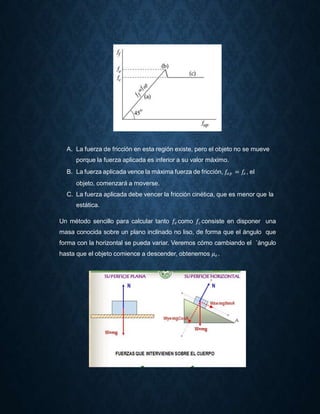
Las leyes de Newton explican el movimiento de los cuerpos y son la base de la mecánica clásica. La primera ley establece que un cuerpo permanece en reposo o movimiento rectilíneo uniforme a menos que actúe una fuerza sobre él. La segunda ley relaciona la fuerza neta sobre un cuerpo con su aceleración. La tercera ley establece que a toda acción le corresponde una reacción igual y de sentido contrario. Juntas, estas leyes permiten explicar gran parte de los fenómenos relacionados con el movimiento.