Este documento presenta información sobre varios proyectos de investigación relacionados con la dinámica de estructuras. Incluye una breve descripción del libro "Dinámica de Estructuras con CEINCI-LAB" de Roberto Aguiar Falconí, así como proyectos de reforzamiento sísmico de estructuras afectadas por el terremoto de 2016 en Ecuador y el proyecto de reforzamiento sísmico del Banco Central de Manta. También proporciona información sobre las publicaciones y proyectos del autor Roberto Aguiar.


















![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
9
1.2 PROGRAMA v_libre Y COMENTARIOS
El programa v_libre encuentra la respuesta en el tiempo de un sistema de un grado de
libertad, sometida a vibración libre. Se puede tener cualquiera de los cuatro casos indicados en
el apartado anterior o una combinación de ellos. Los datos de entrada del programa, son:
zi Es un vector que contiene los factores de amortiguamiento. Está programado
para que dibuje la respuesta en el tiempo para 2 valores de . Si solo se tiene
un solo valor de , copiar dos veces ese valor.
w Frecuencia natural de vibración.
qo Desplazamiento inicial para
qpo Velocidad inicial para
function v_libre(zi,w,qo,qpo)
%
% Vibraciones libres en sistemas de un grado de libertad
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% 5 de octubre de 2011
%-------------------------------------------------------------
% vlibre(zi,w,qo,qpo)
%-------------------------------------------------------------
% zi: Vector que contiene dos factores de amortiguamiento para
% los cuales se encuentra la respuesta en el tiempo.
% w : frecuencia natural del sistema de 1 gdl.
% qo: desplazamiento en t=0
% qpo: velocidad en t=0
% tmax: tiempo maximo de la respuesta igual a 0.6 segundos.
t=linspace(0,0.6,1000)';
np=length (zi); % np es el número de factores de amortiguamiento
for i=1:np
if zi(i)<1
wa=w*sqrt(1-zi(i)*zi(i));
B=qo;A=(qpo+zi(i)*w*B)/wa;q1=(A*sin(wa*t)+B*cos(wa*t));
q2=exp(-zi(i)*w*t); q(:,i)=q2.*q1;
elseif zi(i)==1
B=qo; A=qpo+B*w;q(:,i)=(A*t+B).*exp(-w*t);
else
landa1=-zi(i)*w+w*sqrt(zi(i)*zi(i)-1);
landa2=-zi(i)*w-w*sqrt(zi(i)*zi(i)-1);
C=[1 1; landa1 landa2]; D=[qo; qpo];
X=CD; A=X(1); B=X(2);
q(:,i)=A*exp(landa1*t)+B*exp(landa2*t);
end
end
plot (t,q(:,1),'r','LineWidth',2); hold on; plot (t,q(:,2), 'LineWidth',2)
xlabel ('Tiempo'); ylabel ('Desplazamiento')
title ('Vibracion libre en sistema de 1 gdl')
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-20-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
10
EJEMPLO 5
Encontrar la respuesta en el tiempo de la estructura que se ha venido analizando pero
para dos casos de amortiguamiento y . Comentar los resultados orientados al
Diseño Sismo Resistente.
SOLUCIÓN
>> zi=[0.05;0.25]; w=31.416; qo=2;qpo=10;
>> v_libre(zi,w,qo,qpo)
Figura 1.5 Respuesta en el tiempo que se obtiene con programa v_libre
En la figura 1.5 se indica lo que reporta el programa v_libre. Si bien es cierto la gráfica
corresponde a un caso de vibración libre, no es menos cierto que los comentarios que se
indican a continuación son aplicados a la Ingeniería Sismo Resistente, en lo referente al
amortiguamiento.
La diferencia entre las dos curvas de la figura 1.5, es notable. Mientras más
amortiguamiento tiene la estructura menor es la respuesta. Por lo tanto, se debe
conferir amortiguamiento a la estructura para que se mueva menos durante un sismo y
la forma de hacerlo es mediante la incorporación de disipadores de energía visco
elásticos (Aguiar, 2008) o aisladores de base (Aguiar et al. 2008).
En las estructuras sin sistemas de control pasivo (sin disipadores o aisladores), se verá
más adelante que a mayor amortiguamiento, más daño se espera en la estructura. De
esta manera se comportan las estructuras tradicionales, en este caso no conviene que
la estructura incursione demasiado en el rango no lineal; no conviene que tenga un
alto debido a que se tiene más daño.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-21-320.jpg)







![SISTEMAS DE UN GRADO DE LIBERTAD
18
En la figura 1.11 se presenta el factor de amplificación dinámica, en función de la
relación de frecuencias r , y para valores del factor de amortiguamiento desde 0.01 a 0.5.
De esta figura y de la ecuación (1.25) se tienen los siguientes comentarios:
Para el caso de vibración forzada, sin amortiguamiento 0
y para 1
r en la
ecuación ( 1.25 ) se tiene que
, que constituye el pico principal de resonancia.
A medida que aumenta el factor de amplificación dinámica disminuye.
Para 1
r el valor de tiene un máximo valor para factores de amortiguamiento
menores a 0.15. Tener 1
r significa que la frecuencia de la excitación es igual a la
frecuencia natural del sistema y para estos casos el factor de amplificación dinámica es
mayor que la unidad.
A medida que el valor de se incrementa más ancho es el pico de amplitudes
máximas.
A continuación se presenta el programa FAD que obtiene en forma gráfica el factor de
amplificación dinámica para cuatro valores del factor de amortiguamiento . La forma de
uso del programa, en MATLAB es la siguiente:
[f] = fad(z1,z2,z3,z4)
Como ejemplo de aplicación, se desea encontrar las curvas del factor de amplificación
para valores de igual a 0.01, 0.1, 0.15 y 0.5.
[f] = fad(0.01,0.1,0.15,0.5)
En la figura 1.12 se indican las curvas que se encuentran en el MATLAB, para los
datos indicados.
function [f]=fad(z1,z2,z3,z4)
%
% Factor de Amplificación Dinámica
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% ---------------------------------------
% [f]=fad(z1,z2,z3,z4)
% ---------------------------------------
% z1: Factor de amortiguamiento 1
% z2: Factor de amortiguamiento 2
% z3: Factor de amortiguamiento 3
% z4: Factor de amortiguamiento 4
% r : Relación entre la frecuencia excitación a frecuencia natural
% f : Factor de amplificación dinámica
hold off
dr=0.02;r=0;
for i=1:150
r=r+dr;
f(i)=1.0/(sqrt((1-r^2)^2+(2*z1*r)^2));f1(i)=1.0/(sqrt((1-r^2)^2+(2*z2*r)^2));
f2(i)=1.0/(sqrt((1-r^2)^2+(2*z3*r)^2));f3(i)=1.0/(sqrt((1-r^2)^2+(2*z4*r)^2));
rr(i)=r;
end
plot (rr,f); hold on
plot (rr,f1,'--'); plot (rr,f2,':'); plot (rr,f3,'-.')
xlabel('r'); ylabel('Factor de amplificacion');](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-29-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
19
axis([0,3,0,5]);
text (2.0,4.5,'z1 ---- ','Fontname','symbol'); text (2.0,4.0,'z2 - - -','Fontname','symbol')
text (2.0,3.5,'z3 .......','Fontname','symbol'); text (2.0,3.0,'z4 .-.-.-','Fontname','symbol')
hold off
% ---fin---
1.4.3 Fuerza transmitida a la fundación
Se ha visto que la solución de la ecuación diferencial ( 1.16 ) en régimen permanente
viene dada por:
t
sen
X
q
De donde la derivada con respecto al tiempo es:
t
X
q cos
.
La fuerza que llega a la cimentación, t
f , viene dada por la contribución de la fuerza del
resorte,
k
t
f , más la contribución de la fuerza del amortiguador
c
t
f .
t
X
c
t
sen
X
k
f
q
c
q
k
f
f
f
t
c
t
k
t
t
cos
.
Figura 1.12 Curvas que se obtienen con programa FAD en MATLAB.
Nuevamente se tiene la suma de dos armónicos por lo que la fuerza transmitida a la
fundación vale:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-30-320.jpg)






![SISTEMAS DE UN GRADO DE LIBERTAD
26
golpe a un sistema, a esto se llama Acción de Percusión y el modelo numérico se denomina
delta de dirac
, -
En este modelo se cumple, lo siguiente:
∫ ∫
Donde es un instante antes de que se aplique el golpe (martillazo) y es un
instante después de aplicarse el golpe.
1.6.1 Respuesta en ausencia de condiciones iniciales
Se define al Impulso como el producto de la Velocidad por la Masa, también se conoce
con el nombre de Momentum. Ahora bien se desea encontrar la respuesta en el tiempo de un
sistema de un grado de libertad, como el indicado en la figura 1.19 si la fuerza es un golpe.
León (1981).
Figura 1.19 Descripción del problema ante un Impulso Unitario
Como la fuerza (martillazo) se aplica en un instante de tiempo tan pequeño, el
desplazamiento inicial es cero. Pero la velocidad inicial no y esta es igual al Impulso dividido
para la masa. Luego las condiciones iniciales que se generan por el golpe dado al sistema son:
̇
En la ecuación (1.33) se tiene la respuesta en el tiempo para un pulso rectangular,
esta vale para
Pero (Impulso Unitario) y además . Al reemplazar todo esto en la expresión
anterior se encuentra luego de factorar .
[ ]
A la respuesta a un Impulso Unitario se le denomina . Luego:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-37-320.jpg)


![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
29
Se define la función de transferencia en el campo complejo como la relación entre
la respuesta (salida) y la excitación (entrada) Barbat y Canet (1994)
Por lo tanto, la respuesta en el dominio de las frecuencias viene dada por:
Al remplazar (1.47) en la primera ecuación de (1.45) se halla.
∫
1.10 INTEGRAL DE DUHAMEL
La solución de la ecuación diferencial (1.42) está compuesta por una solución
homogénea y una solución particular. La solución homogénea se obtiene sin considerar la
acción sísmica es decir igualando a cero; esta solución ya fue presentada cuando se estudio
vibraciones libres.
La solución particular queda determinada por la Integral de Duhamel, la misma que se
presenta a continuación.
∫
Donde es la frecuencia amortiguada (ecuación 1.9); es la frecuencia natural
(ecuación 1.3); es el factor de amortiguamiento; es la aceleración del suelo.
La solución homogénea desaparece en los primeros instantes por lo que la respuesta
del sistema tiene solamente el aporte de la solución particular, por este motivo en lugar de
escribir se denominará .
Al resolver las funciones exponencial y trigonométrica, indicada en la ecuación (1.49)
se obtiene:
∫ [ ]
La ecuación (1.50) puede escribirse de la siguiente manera:
[ ]
∫
∫
Las integrales indicadas en las ecuaciones (1.52) y (1.53) pueden resolverse con
Métodos Numéricos pero en este capítulo, no se lo va a realizar de esa manera sino que se
pretende encontrar una solución analítica lo más exacta posible ya que en el próximo capítulo
se resuelve con el Método de Newmark.
Es lo más exácta posible ya que la eceleración del sismo, se la discretiza y se
considera que la variación entre dos instantes de tiempo y es lineal, como se muestra en
(1.46)
(1.47)
(1.48)
(1.49)
(1.50)
(1.51)
(1.52)
(1.53)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-40-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
30
la figura 1.21. Para un instante de tiempo en el intervalo indicado la variación de la aceleración
está definida por la ecuación de una recta, con pendiente
Figura 1.21 Variación lineal de la excitación.
Al reemplazar la ecuación (1.54) en (1.52) y (1.53), se obtiene las variables en el
tiempo discreto . (Barbat y Caicedo, 1992),
[ ]
[ ]
Los límites de integración de las ecuaciones (1.55) y (1.56) son desde hasta
El programa Duhamel encuentra la respuesta en el tiempo de: desplazamiento,
velocidad y aceleración de un sistema de un grado de libertad sometido a una acción sísmica.
Los datos del programa, son:
p Archivo que contiene las aceleraciones del sismo.
dt Incremento de tiempo del archivo de aceleraciones.
m Masa del sistema.
k Rigidez del sistema.
zeda Factor de amortiguamiento.
function Duhamel (p,dt,m,k,zeda)
%
% Programa para encontrar la respuesta en el tiempo
% de un sistema de un grado de libertad aplicando la
% Integral de Duhamel
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% 12 de octubre de 2011
%-------------------------------------------------------------
% duhamel(p,m,k,zeda)
%-------------------------------------------------------------
(1.54)
(1.55)
(1.56)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-41-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
31
% p: Archivo que contiene al acelerograma
% dt: Incremento de tiempo del acelerograma entre dos puntos discretos
% m: Masa del sistema de un grado de libertad
% k: Rigidez del sistema de un grado de libertad
% zeda: Factor de amortiguamiento
%-------------------------------------------------------------
w=sqrt(k/m);wa=w*(1-zeda*zeda); % Frecuencias sin y con amortiguamiento
np=length(p); % Numero de puntos del acelerograma
q(1)=0;qp(1)=0; %Condiciones iniciales nulas
Asum=0; Bsum=0;
for i=2:np
a1=p(i-1); %Aceleración en tiempo discreto i-1
t1=dt*(i-1); %Tiempo
a2=p(i); %Aceleración en tiempo discreto i
t2=dt*i;t(i)=t2; %Tiempo
s=(a2-a1)/(t2-t1); % Pendiente de variación de la aceleración (sismo)
valA1=Aintegral(s,a2,t2,zeda,w,wa);valA2=Aintegral(s,a1,t1,zeda,w,wa);
Asum=Asum+valA1-valA2;
valB1=Bintegral(s,a2,t2,zeda,w,wa);valB2=Bintegral(s,a1,t1,zeda,w,wa);
Bsum=Bsum+valB1-valB2;
q(i)=exp(-zeda*w*t2)/wa*(Asum*sin(wa*t2)-Bsum*cos(wa*t2));
qp(i)=exp(-zeda*w*t2)*(Asum*cos(wa*t2)+Bsum*sin(wa*t2))-w*zeda*q(i);
qpp(i)=-w*w*q(i)-2*zeda*w*qp(i);
end
figure(1)
plot (t,q,'LineWidth',1.5);xlabel ('Tiempo'); ylabel ('Desplazamiento')
figure(2)
plot (t,qp,'LineWidth',1.5);xlabel ('Tiempo'); ylabel ('Velocidad')
figure (3)
plot(t,qpp,'LineWidth',1.5);xlabel ('Tiempo'); ylabel ('Aceleracion')
% fin
function [valor]=Aintegral(m,a,t,zeda,w,wa)
fac1=(zeda*w*a+m*(1-2*zeda*zeda))*cos(wa*t);
fac2=(wa/w)*(w*a-2*zeda*m)*sin(wa*t);
valor=exp(zeda*w*t)/(w*w)*(fac1+fac2);
return
function [valor1]=Bintegral(m,a,t,zeda,w,wa)
fac11=(zeda*w*a+m*(1-2*zeda*zeda))*sin(wa*t);
fac22=(wa/w)*(w*a-2*zeda*m)*cos(wa*t);
valor1=exp(zeda*w*t)/(w*w)*(fac11+fac22);
return
EJEMPLO 8
Encontrar la respuesta en el tiempo, de la estructura indicada en la figura 1, ante el
registro obtenido en la estación Sylmar, durante el sismo de Northridge del 17 de enero de
1994, que tuvo una magnitud de 6.7. El acelerograma tuvo una aceleración máxima de 826.76
gals. Se considera un factor de amortiguamiento
SOLUCIÓN
Como complemento a la información sísmica se debe indicar que el registro de Sylmar
fue obtenido en un suelo de bastante resistente (Clasificación tipo B según el Servicio
Sismológico de los Estados Unidos con velocidades de la onda de corte comprendidas entre
360 y 750 m/s), la estación se encontraba a 18 km., de la zona epicentral. Es un sismo
impulsivo cuya fase intensa tuvo una duración de 2 seg.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-42-320.jpg)











![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
43
M
Q
q i
..
iv. Se encuentra el incremento de velocidad
.
q
t
q
t
q
q i
2
..
..
.
v. Se determina el incremento de desplazamiento q
2
..
2
..
.
6
2
t
q
t
q
t
q
q i
i
vi. Se obtiene el nuevo desplazamiento, velocidad y aceleración en 1
i
t
..
..
1
..
.
.
1
.
1
q
q
q
q
q
q
q
q
q
i
i
i
i
i
i
vii. Los valores obtenidos en el tiempo 1
i
t se asignan a i
t
1
..
..
1
.
.
1
i
i
i
i
i
i
q
q
q
q
q
q
Para un nuevo incremento de tiempo se repite desde el paso dos. Es importante
destacar que en el Análisis Lineal, la masa equivalente
M se determina una sola vez.
2.2 PROGRAMA lineal
El programa lineal, halla en forma gráfica, la respuesta en el tiempo de un sistema de
un grado de libertad, ante una acción sísmica, definida por su acelerograma, aplicando el
Método de Aceleración Lineal indicado en el apartado anterior.
El programa ha sido elaborado en MATLAB y antes de utilizarlo se debe grabar el
archivo que contiene únicamente las aceleraciones del sismo en formato ASCII. El nombre
tiene extensión .dat. Después de ello cuando se encuentra en la modalidad consola se carga
el acelerograma y después se ejecuta lineal, de la siguiente manera:
[d,v,a] = lineal (p,m,c,k,dt)
p es el nombre del archivo que contiene el acelerograma.
m es la masa del sistema de 1 gdl.
c es el amortiguamiento del sistema de 1 gdl.
k es la rigidez del sistema de 1 gdl.
(2.5)
(2.6)
(2.7)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-54-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
44
dt es el incremento de tiempo con el cual se desea hallar la respuesta. El mismo que
tiene que ser igual al incremento de tiempo con el cual se obtuvo el acelerograma.
Una vez que se ejecuta lineal aparecen cuatro gráficas, la primera de ellas es el
acelerograma, que es dato. La segunda la respuesta en el tiempo de los desplazamientos, la
tercera de las velocidades y la última de las aceleraciones.
function [d,v,a]=lineal(p,m,c,k,dt)
%
% Respuesta en el tiempo de un sistema de un grado de libertad
% por el Método de la Aceleración Lineal
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
%------------------------------------------------------------------
% [d,v,a]=lineal(p,m,c,k,dt)
%------------------------------------------------------------------
% p : vector que contiene los registros del acelerograma
% m : masa del sistema
% c : amortiguamiento del sistema
% k : rigidez del sistema
% d, v, a : desplazamiento, velocidad y aceleración de la respuesta
% dt : incremento de tiempo
%
n=length(p); tmax=dt*n; t=linspace(0,tmax,n)';
ma=m+(c*dt/2)+(k*dt*dt/6);
d(1)=0; v(1)=0; a(1)=0;
for i=1:n-1
dq=-m*(p(i+1)-p(i));
dqa=dq-a(i)*(c*dt+k*dt*dt/2)-v(i)*k*dt;
inca=dqa/ma; incv=a(i)*dt+inca*dt/2; incd=v(i)*dt+a(i)*dt*dt/2+inca*dt*dt/6;
d(i+1)=d(i)+incd; v(i+1)=v(i)+incv; a(i+1)=a(i)+inca;
d(i)=d(i+1); v(i)=v(i+1); a(i)=a(i+1);
end
subplot (4,1,1); plot (t,p); title('Acelerograma');
subplot (4,1,2); plot (t,d); ylabel('Desplazamiento');
subplot (4,1,3); plot (t,v); ylabel('Velocidad');
subplot (4,1,4); plot (t,a);xlabel('Tiempo'); ylabel('Aceleracion');
%---fin---
EJEMPLO 1
Hallar la respuesta en el tiempo del oscilador indicado en la figura 2.1, que tiene una
masa
cm
s
T
m
2
004898
.
0
, una frecuencia natural
s
Wn
1
2832
.
6
y un coeficiente de
amortiguamiento 05
.
0
. Ante el sismo del 9 de noviembre de 1974, registrado en el Perú.
El acelerograma fue obtenido a 80 Km., del epicentro sobre un suelo limo arcilloso. El evento
tuvo una magnitud de 6. La aceleración máxima del sismo, en valor absoluto fue de 117 gals
(cm/s
2
). El incremento de tiempo con el cual fue obtenido el registro es s
t 02
.
0
.
SOLUCIÓN
Para utilizar el programa lineal se debe determinar el amortiguamiento y la rigidez del
sistema, en base a la frecuencia natural y al coeficiente de amortiguamiento.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-55-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
45
cm
T
m
W
k
m
k
W n
n /
19336619
.
0
004898
.
0
*
4786
.
39
/ 2
2
Figura 2.1 Modelo de un sistema de 1 gdl.
cm
Ts
mk
c
mk
c /
0030775
.
0
193366
.
0
*
004898
.
0
*
05
.
0
*
2
2
2
/
El período del sistema que se analiza es n
W
T /
2
= 1 s. Una vez cargado el
acelerograma como un vector, en la modalidad consola, se ejecuta el programa lineal.
>>load Peru04.dat
>>[d,v,a] = lineal (Peru04, 0.004898, 0.00307751136, 0.19336619, 0.02)
Es importante tener muy en cuenta las unidades. Si el acelerograma viene en gals.
Se debe trabajar todo con cm y s. Así es como se ha procedido en el ejemplo realizado.
En la figura 2.2 se indica la respuesta en el tiempo del sistema de 1 gdl., del ejemplo 1.
Como se indicó aparece el acelerograma, los desplazamientos, velocidad y aceleración.
Se puede hallar las respuestas máximas, en valor absoluto, desde la modalidad
consola de la siguiente manera:
>>Sd=max(abs(d))
Sd=
2.9842
>>Sv=max(abs(v))
Sv=
23.8650
>>Sa=max(abs(a))
Sa=
213.5134
Se ha denominado Sd, Sv, Sa a la máxima respuesta, en valor absoluto, de los
desplazamientos, velocidades y aceleraciones, respectivamente.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-56-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
47
grado de libertad, en base a una columna con una masa puntual. Lo importante es que el lector
observe que todos ellos, son formas de representar un sistema de 1 gdl.
Por su sencillez en el dibujo, se utilizará en el presente capítulo el último modelo
compuesto por una columna y la masa puntual.
EJEMPLO 2
Hallar la respuesta en el tiempo de un sistema cuya masa es 0.0024 Ts
2
/cm, la rigidez
es 0.023687 T/cm y el amortiguamiento vale 0.000753981 Ts/cm. Ante el sismo utilizado en el
ejemplo 1.
SOLUCIÓN
El sistema de 1 gdl del ejercicio anterior, tenía un período de vibración de 1 segundo y
el de este ejercicio, tiene un período de 2 segundos. Es importante tener esto presente para el
tema que se tratará en el próximo apartado.
>>load Peru04.dat
>>[d,v,a] = lineal (Peru04, 0.0024, 0.000753981, 0.023687, 0.02)
La respuesta en desplazamientos, velocidades y aceleraciones, que reporta el
MATLAB, al utilizar el programa lineal, se indica en la figura 2.4. Por otra parte, las respuestas
máximas son: cm
Sd 6702
.
2
. .
/
0933
.
15 s
cm
Sv y
2
/
5191
.
129 s
cm
Sa .
2.4 ESPECTROS DE RESPUESTA
Por los años de 1915, Naito diseñaba sus estructuras ante sismos considerando como
fuerzas laterales una fracción del peso de sus elementos y sus edificaciones tuvieron un buen
comportamiento durante el sismo de Tokyo de 1923 lo que no ocurrió con otras edificaciones
que colapsaron. El primer código de diseño sísmico del mundo fue el de Japón de 1919.
(Rosenblueth, 1965)
A partir de 1930 se reconoció el problema sísmico como un problema de dinámica de
estructuras y ya se empezaron a definir modelos numéricos de cálculo, en los que se
establecieron bien las variables involucradas (Suyehiro, 1932; Freeman, 1932; Biot, 1943). En
1934 Benioff introduce la definición de espectro de respuesta. Sin embargo de esto todavía
existen proyectistas estructurales que a lo mucho la naturaleza dinámica del problema sísmico,
la consideran al calcular el cortante basal Vo; por otra parte, determinan el período de vibración
T de la estructura utilizando ecuaciones muy elementales, lo propio realizan con la
determinación de las fuerzas laterales estáticas equivalentes. Existen importantes avances en
el análisis lineal y no lineal de estructuras que deben ser acogidas.
En 1952, Housner presenta el pseudo espectro de velocidades. Luego en 1959,
Housner propuso el primer grupo de formas espectrales promedio, normalizando para el efecto
8 registros obtenidos de los siguientes terremotos: El Centro 1934 y 1940, Western
Washington, (Olympia) 1949 y Kerb County (Taft) 1952. Nótese que ya se empieza con el tema
del espectro de diseño que será abordado en el siguiente capítulo en forma extensa.
2.4.1 Definición de espectro
Se define el espectro de respuesta como la respuesta máxima de un conjunto de
osciladores de 1 gdl que tienen el mismo amortiguamiento, sometidas a una historia de
aceleraciones dadas.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-58-320.jpg)


![SISTEMAS DE UN GRADO DE LIBERTAD
50
La forma de utilizar el programa espectro es:
>> [Sd,Sv,Sa] = espectro (p,dt,zeda)
Sd Matriz que contiene los desplazamientos espectrales para diferentes valores de .
Sv Matriz que contiene las velocidades espectrales para diferentes valores de .
Sa Matriz que contiene las aceleraciones espectrales para diferentes valores de .
p Vector que contiene las aceleraciones del suelo para el cual se hallan los espectros
dt Incremento de tiempo con el cual se halla la respuesta, igual al incremento de
tiempo del acelerograma.
zeda Vector que contiene los valores de para los cuales se desean los espectros.
El período obtiene los espectros, desde un período inicial igual a 0.01 s., hasta un
período máximo de 3.0 s., con un incremento en los períodos de 0.03 s. De tal manera que se
calculan los espectros en base a 100 osciladores, si se desea incrementar el número de
osciladores se debe disminuir el incremento de período. Cualquiera de estos valores se puede
modificar al ingresar al programa espectro
Antes de utilizar el programa, se debe cargar el archivo de datos en el cual se halla el
acelerograma y el vector que contiene los valores, del factor de amortiguamiento para los
cuales se desea encontrar los espectros.
function [Sd,Sv,Sa]=espectro(p,dt,zeda)
%
% Espectros de respuesta elástica de: desplazamientos, velocidad y aceleración.
% Empleando Método de Aceleración Lineal.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%
%------------------------------------------------------------------------------------------------
% [Sd,Sv,Sa]=espectro(p,dt,zeda)
%------------------------------------------------------------------------------------------------
%
% p Vector que contiene el acelerograma.
% dt Intervalo de tiempo con el que se halla la respuesta igual al
% valor con que fueron tomados los datos del acelerograma.
% zeda Vector que contiene los valores de amortiguamiento.
% Sd Valores máximos de los desplazamientos en absoluto.
% Sv Valores máximos de las velocidades en absoluto.
% Sa Valores máximos de las aceleraciones en absoluto.
% DT Intervalo de Periodos = 0.03 s.
% Tmin Período mínimo que se considera igual a 0.01 s.
% Tmax Período máximo que se considera igual a 3.00 s.
%
hold off; Tmin=0.01; Tmax=3.0; DT=0.03; n=((Tmax-Tmin)/DT)+1;
m=length(zeda); T=linspace(Tmin,Tmax,n)'; W=2*pi./T; K=W.*W;
for i=1:m
zi=zeda(i); C=(2*zi).*sqrt(K);
for j=1:n
xj=K(j); yj=C(j);
[d,v,a]=lineales(p,1,yj,xj,dt);
Sd(i,j)=max(abs(d)); Sv(i,j)=max(abs(v)); Sa(i,j)=max(abs(a));
end
end](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-61-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
51
subplot (3,1,1); plot (T,Sd); ylabel('Desplazamiento'); title('ESPECTROS DE
DESPLAZAMIENTO, VELOCIDAD Y ACELERACION RELATIVA')
hold on
subplot (3,1,2); plot (T,Sv); ylabel('Velocidad');
hold on
subplot (3,1,3); plot (T,Sa);xlabel('PERIODO'); ylabel('Aceleracion'); hold off
%---fin---
EJEMPLO 3
Hallar los espectros de respuesta elástica de desplazamiento, velocidad y aceleración
del sismo del 9 de noviembre de 1974, para valores de igual a: 0.05; 0.10 y 0.20.
SOLUCIÓN
>> load Peru04.dat
>> zeda=[0.05; 0.10; 0.20]
>> [Sd,Sv,Sa]=espectro (Peru04,0.02,zeda)
En la figura 2.6 se ha indicado los espectros que reporta el programa espectro. Los
comentarios que se realizan al respecto, son los siguientes:
La identificación del tipo de línea, que se encuentra en la parte inferior de la figura 2.6
se lo realizó con el programa PAINT.
El último de los espectros es de aceleración relativa. No se ha encontrado el espectro
de aceleración absoluta. La diferencia entre los dos, radica en que el espectro de
aceleraciones relativas, se encuentra de la respuesta máxima en valor absoluto de las
aceleraciones
..
)
(t
q . En cambio, para hallar de la aceleración absoluta se debe hallar
el valor máximo en valor absoluto de
..
..
)
(
)
( t
U
t
q g
, es decir se debe sumar la
aceleración del suelo.
A medida que los valores de se incrementan, las formas espectrales disminuyen.
Al presentar los tres espectros de respuesta de: desplazamiento, velocidad y
aceleración relativa, en un solo gráfico, la escala vertical se redujo con lo que se
deforma un poco las formas espectrales.
Se denominan espectros de respuesta, ya que son espectros para un determinado
sismo. Los espectros de diseño se obtienen en base a los espectros de respuesta de
varios sismos, como se ilustra en el próximo capítulo.
2.5 USO DEL PROGRAMA DEGTRA
Un programa muy versátil para el análisis dinámico de sistemas de 1 gdl es el
programa DEGTRA A4 desarrollado por Ordaz y Dulché (2002) en el Instituto de Ingeniería de
la Universidad Nacional Autónoma de México. En realidad son más los investigadores que han
aportado al desarrollo de este programa entre ellos están Jorge Arboleda y Mauricio Gallego.
Una vez que se tiene instalado el programa DEGTRA, lo primero que se debe hacer,
es abrir una ventana para lo cual se selecciona el icono que está indicado con una flecha en la
figura 2.7.
Después se busca el archivo en el cual se halla el acelerograma, para el efecto se
selecciona el icono que está indicado en la figura 2.8.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-62-320.jpg)


























![SISTEMAS DE UN GRADO DE LIBERTAD
78
Tabla 3.7 Sismos recomendados por el Comité VISION 2000 para edificios
Sismo Vida Útil
T
Probabilidad de
Excedencia
P
Período medio
de retorno, r
t
Tasa Anual de
excedencia, 1
p
Frecuente 30 años 50% 43 años 0.02310
Ocasional 50 años 50% 72 años 0.01386
Raro 50 años 10% 475 años 0.00211
Muy raro 100 años 10% 970 años 0.00105
La mayor parte de normativas sísmicas presentan únicamente el espectro para el
sismo Raro y surge el problema, para el Proyectista Estructural, que no va a contratar estudios
de Peligrosidad Sísmica, como encontrar formas espectrales para los restantes sismos
indicados en la tabla 3.6.
Por este motivo, es que en los años 2002 y 2003 se empezó a recopilar estudios de
Peligrosidad Sísmica, realizados para los períodos de retorno indicados en la tabla 3.7, en
América del Sur y que estipulan algunas normas al respecto, con esta información en Aguiar
(2003) se presenta una propuesta de cómo hallar espectros elásticos para los sismos:
Frecuente, Ocasional y Muy Raro, a partir del espectro para el sismo Raro. La propuesta se
resume a continuación.
Para el Sismo Frecuente se dividen las ordenadas espectrales del Sismo Raro para 3
y posteriormente se ajusta la forma espectral para un amortiguamiento del 2%,
empleando las ecuaciones propuestas por Newmark y Hall, que se indican a
continuación:
ln
68
.
0
21
.
3
a
ln
27
.
0
82
.
1
ln
41
.
0
31
.
2
d
v
Las ecuaciones denominadas (3.4) tienen un 50% de probabilidad de excedencia. Por
otra parte, en estas ecuaciones c
b
a
,
, , son los factores de amplificación para la
aceleración, velocidad y desplazamiento. Existe otra ecuación más sencilla, que
también se puede hallar para pasar del espectro que está calculado para un 05
.
0
a un 02
.
0
Esta es:
04
.
0
5
a
f
En la ecuación (3.5) el valor de se indica en porcentaje.
Para el Sismo Ocasional se multiplica el sismo frecuente por 1.4
Para el Sismo muy raro se multiplica el sismo raro por 1.3
Se ha elaborado un programa en MATLAB denominado Vision que determina los
cuatro espectros, para análisis sísmico por desempeño. La forma de uso del programa es:
[saf,sao,sar,sam]=Vision (A0)
A0 es la aceleración máxima del suelo en gals, definida en el Código Ecuatoriano de
la Construcción, varía desde 392 gals en la zona de mayor peligrosidad sísmica, hasta
147 gals.
(3.5)
(3.4)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-89-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
79
Posteriormente, por pantalla se debe indicar un código que identifica el perfil de suelo.
Para un perfil de suelo S1, el código es 1; para un suelo S2 el código es 2; para suelo
S3 es 3 y para suelo S4 es 4.
function [saf,sao,sar,sam]=Vision(a0);
%
% ESPECTROS POR DESEMPEÑO
%
% Por: Roberto Aguiar
% ESPE
%
%--------------------------------------------------------------------------
% [saf,sao,sar,sam]=Vision(a0)
%--------------------------------------------------------------------------
% a0 : Aceleración del suelo en roca en gal definido en la zona sismica
% Ta : Periodo donde termina la aceleracion constante
% Tm : Periodo donde termina la aceleracion descendente
% beta : Parámetro por tipo de suelo
% s : Parámetro por tipo de suelo
% alfa : Coeficiente de importancia
% is : Código del perfil de suelo
%
alfa=1.0;
fprintf ('n Códigos para perfiles de suelo: S1=1 S2=2 S3=3 S4=4');
is=input ('n Indique el código :');
if is==1
ta=0.50; tm=2.50; beta=2.5; s=1.0;
elseif is==2
ta=0.52; tm=3.11; beta=3.0; s=1.2;
elseif is==3
ta=0.82; tm=4.59; beta=2.8; s=1.5;
else
ta=2.0; tm=10.0; beta=2.5; s=2.0;
end
tmin=0.01; tmax=3.0; n=100; dt=(tmax-tmin)/n;
hold off
for i=1:n;
t(i)=i*dt;
if t(i)<=ta;
sar(i)= alfa*beta*a0;
elseif t(i)<=tm & t(i)>ta;
sar(i)= (1.25*alfa*a0*(s^s))/t(i);
else
sar(i)= (alfa*a0)/2;
end
saf(i)=sar(i)/3; sao(i)=saf(i)*1.4; sam(i)=sar(i)*1.3;
end
plot(t,saf);
hold on
plot(t,sao,'--'); plot(t,sar),':'; plot(t,sam),'-.';
xlabel ('Periodo (s)'); ylabel ('Aceleracion (gal)')
hold off
end](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-90-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
80
En el programa VISION no se ha realizado la corrección de las formas espectrales por
el factor de amortiguamiento, para los sismos frecuente y ocasional.
EJEMPLO 2
Ilustrar el uso del programa VISION para hallar los espectros por desempeño, para la
zona de mayor peligrosidad sísmica del Ecuador )
/
392
4
.
0
( 2
0 s
cm
g
A
en un perfil de
suelo S3.
SOLUCION
[saf,sao,sar,sam]=Vision (392)
Por pantalla se digitará el número 3, para indicar que corresponde al perfil de suelo S3.
En la figura 3.11 se indican los espectros de desempeño que reporta el programa.
Figura 3.11 Espectros para un perfil de suelo S3 en la zona de mayor peligrosidad sísmica.
FEMA 273 (1997) y NEHRP (2003) recomiendan nuevos períodos de retorno para
edificios que son más exigentes como se observa en la figura 3.8; el sismo frecuente pasa de
43 años a 72 años; el ocasional de 72 a 225 años y el muy raro de 970 a 2475 años. De tal
manera que se están tomando mayores precauciones sísmicas y habrá que esperar cuales son
las futuras recomendaciones cuando se tome en cuenta las grandes pérdidas dejadas por el
Mega Sismo de Chile de 2010. (Aguiar, 2011) En el mega sismo las pérdidas económicas se
estimaron en 30000 millones de dólares, las pérdidas humanas sobrepasaron las 500
personas. Muchos edificios de altura en Santiago de Chile, no colapsaron durante el mega
sismo pero la rehabilitación de los mismos será muy costosa, de ahí la necesidad de verificar
el desempeño sísmico de las estructuras tema que se aborda en el siguiente apartado.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-91-320.jpg)














![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
95
contrario para períodos grandes el desplazamiento máximo inelástico es igual al
desplazamiento máximo elástico y para los períodos intermedios se tienen valores
intermedios determinados por las ecuaciones (3.17).
El programa denominado newmakhall permite encontrar el factor de reducción para
algunos valores de ductilidad, el usuario en la modalidad consola mediante el vector u indicará
los valores de ductilidad para los cuales desea calcular el factor
R . El uso del programa es:
[Ru] = newmarkhall (u)
u Vector que contiene las ductilidades para las cuales se desea calcular
R .
function [Ru]=newmarkhall(u)
%
% Factor de reducción por Ductilidad propuesto por Newmark y Hall (1982)
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-----------------------------------------------------------------------
% [Ru]=newmarkhall(u)
%-----------------------------------------------------------------------
% Ru Factor de reducción por ductilidad
% u Vector que contiene las demandas de ductilidad que se obtienen.
% Ta, Tb Periodos del espectro definidos por Newmark y Hall.
% Tc Periodos característicos del suelo se consideran los del CEC-2000
% T Periodo de vibración de la estructura.
%
m=length(u);
fprintf ('n Códigos para perfiles de suelo: S1=1 S2=2 S3=3 S4=4');
is=input('n Indique el código del tipo de suelo :');
if is==1
Tc=0.50;
elseif is==2
Tc=0.52;
elseif is==3
Tc=0.82;
else
Tc=2.0;
end
Tmin=0.01; Tmax=3.0; n=100; DT=((Tmax-Tmin)/n); Ta=1/33; Tb=0.125; hold off;
for j=1:m
Tac=(sqrt(2*u(j)-1)/u(j))*Tc;
for i=1:n
T(i)=i*DT;
if T(i)<Ta
Ru(i,j)=1;
elseif T(i)>=Ta & T(i)<=Tb
beta=(log10(T(i)/Ta))/(2*log10(Tb/Ta)); Ru(i,j)=(2*u(j)-1)^beta;
elseif T(i)>=Tb & T(i)<=Tac
Ru(i,j)=sqrt(2*u(j)-1);
elseif T(i)>Tac & T(i) <Tc
Ru(i,j)=u(j)*T(i)/Tc;
else
Ru(i,j)=u(j);
end](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-106-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
96
end
end
for j=1:m
if j==1
plot (T,Ru)
elseif j==2
plot (T,Ru,'--')
else
plot (T,Ru,':')
end
hold on
end
xlabel('Periodo (s)'); ylabel ('Factor de Reducción por Ductilidad');
axis([0,3,0,4.5]);
%---fin
EJEMPLO 3
Utilizando el programa newmarhall encontrar los factores de reducción de ductilidad,
para un perfil de suelo S2, de acuerdo a la propuesta de Newmark y Hall (1982), para
ductilidades de 1.5, 2.0, 2.5, 3.0, 3.5 y 4.0
SOLUCIÓN
>> u = [ 1.5; 2.0; 2.5; 3.0; 3.5; 4.0]
>> [Ru]=newmarkhall(u)
En la figura 3.20 se indican las curvas que reporta el programa newmarhall. La
identificación de cada curva se la realizó utilizando PAINT.
Figura 3.20 Factores de reducción por ductilidad utilizando ecuaciones de Newmark y Hall.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-107-320.jpg)












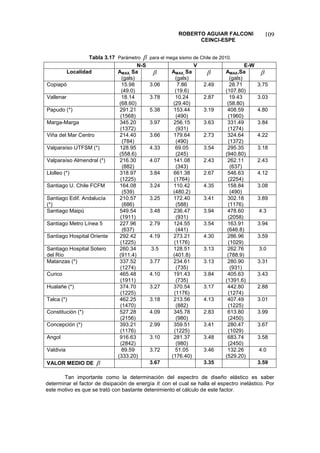






![SISTEMAS DE UN GRADO DE LIBERTAD
116
k
20
.
1510
24
.
609
32
.
329
99
.
743
24
.
609
20
.
1510
24
.
609
32
.
329
24
.
609
32
.
329
Con el propósito de que el lector aprenda MATLAB se presenta un programa que
calcula la matriz de rigidez de un elemento viga sin considerar nudos rígidos, se denomina
kviga y la forma de uso es la siguiente:
[k] = kviga (b,h,L,E)
b es la base de la sección transversal del elemento.
h es la altura de la sección transversal del elemento.
L es la longitud del elemento.
E es el módulo de elasticidad del elemento.
Para el ejemplo 1, los datos de entrada, son:
>> [k]=kviga (0.30,0.30,3.70,2100000)
function [k]=kviga(b,h,L,E)
%
% Matriz de rigidez de un elemento viga sin nudos rigidos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [k]=kviga(b,h,L,E)
%-------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% L: longitud del elemento.
% E: modulo de elasticidad del material
% beta: factor de forma se considera 1.2
G=0.4*E; beta=1.2; inercia=b*h^3/12; area=b*h; fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-2*fi))/(L*(1+4*fi));
kpf=kf; b=(kf+a)/L; bp=b; t=(b+bp)/L;
k(1,1)=t; k(1,2)=b; k(1,3)=-t; k(1,4)=bp; k(2,2)=kf; k(2,3)=-b; k(2,4)=a;
k(3,3)=t; k(3,4)=-bp; k(4,4)=kpf;
for i=1:3;
for j=i+1:4;
k(j,i)=k(i,j);
end
end
fprintf ('n Matriz de Rigidez de Elemento Viga: nn')
for i=1:4
for j=1:4
fprintf ('%10.3f', k(i,j))
end
fprintf('n')
end
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-127-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
118
'
0
'
0
0
0
0
0
'
0
0
k
r
b
t
a
b
k
r
r
b
t
b
t
(4.4)
La variable todavía no definida es:
L
EA
r
Tanto en la matriz (4.4) como en la (4.1) se ha utilizado la minúscula, para identificar
a la matriz de rigidez del elemento, se utiliza la mayúscula para la matriz de rigidez de la
estructura. Por otra parte la negreada es la matriz, en cambio que la es un elemento de la
matriz de rigidez. El programa que obtiene la matriz de rigidez de una columna en coordenadas
globales es kcolumna
function [k]=kcolumna (b,h,L,E)
%
% Matriz de rigidez de un elemento columna sin nudos rigidos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [k]=kcolumna(b,h,L,E)
%-------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% L: longitud del elemento.
% E: modulo de elasticidad del material
% beta: factor de forma se considera 1.2
G=0.4*E; beta=1.2; inercia=b*h^3/12; area=b*h; fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-2*fi))/(L*(1+4*fi));
kpf=kf; b=(kf+a)/L; bp=b; t=(b+bp)/L;r=E*area/L
k=zeros(6);
k(1,1)=t; k(1,3)=-b; k(1,4)=-t; k(1,6)=-bp; k(2,2)=r; k(2,5)=-r;
k(3,3)=kf; k(3,4)=b; k(3,6)=a; k(4,4)=t; k(4,6)=bp; k(5,5)=r; k(6,6)=kpf;
for i=1:5;
for j=i+1:6;
k(j,i)=k(i,j);
end
end
fprintf ('n Matriz de Rigidez de Elemento Columna: nn')
for i=1:6
for j=1:6
fprintf ('%12.3f', k(i,j))
end
fprintf('n')
end
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-129-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
120
Figura 4.4 Geometría de la viga con dos sectores de rigidez infinita.
SOLUCIÓN
Al reemplazar c1 = c2 = 0.15 y los restantes datos indicados en el ejemplo anterior, en
(4.5 ), se obtiene:
k=
39
.
1700
64
.
658
32
.
329
17
.
934
64
.
658
39
.
1700
64
.
658
32
.
329
64
.
658
32
.
329
El programa que determina la matriz de rigidez de un elemento viga, considerando
nudos rígidos, se denomina: kviganr . La forma de uso y los datos de entrada son:
[k]=kviganr(b,h,c1,c2,L,E)
b,h son la base y altura de la sección transversal del elemento.
c1,c2 son la longitudes del nudo rígido, en el nudo inicial y final, respectivamente.
L, E es la luz libre del elemento y el módulo de elasticidad.
function [k]=kviganr(b,h,c1,c2,L,E)
%
% Matriz de rigidez de un elemento viga con nudos rigidos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%--------------------------------------------------------------------
% [k]=kviganr(b,h,c1,c2,L,E)
%--------------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% c1 longitud del nudo rígido en el nudo inicial.
% c2 longitud del nudo rígido en el nudo final.
% L: longitud del elemento de borde a borde sin los nudos rigidos
% E: modulo de elasticidad del material
% beta: factor de forma se considera 1.2
G=0.4*E; beta=1.2; inercia=b*h^3/12; area=b*h; fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-2*fi))/(L*(1+4*fi));
kpf=kf; b=(kf+a)/L; bp=b; t=(b+bp)/L;
k(1,1)=t; k(1,2)=b+c1*t; k(1,3)=-t; k(1,4)=bp+c2*t;
k(2,2)=kf+2*c1*b+c1*c1*t; k(2,3)=-(b+c1*t); k(2,4)=a+c1*bp+c2*b+c1*c2*t;
k(3,3)=t; k(3,4)=-(bp+c2*t); k(4,4)=kpf+2*c2*bp+c2*c2*t;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-131-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
122
Por facilidad de escritura se han presentado la matriz triangular superior de todas las
matrices de rigidez, pero en los respectivos programas se obtiene toda la matriz de rigidez.
Primero se han programado los elementos de la matriz triangular superior y después mediante
dos lazos se ha encontrado los elementos de la matriz triangular inferior, sabiendo que estas
matrices son simétricas, con respecto a la diagonal principal.
EL programa que determina la matriz de rigidez de un elemento columna, con nudos
rígidos se denomina: kcolumnanr
[k]=kcolumnanr(b,h,c1,c2,L,E)
b,h son la base y altura de la sección transversal del elemento.
c1,c2 son la longitudes del nudo rígido, en el nudo inicial y final, respectivamente.
L, E es la luz libre del elemento y el módulo de elasticidad.
function [k]=kcolumnanr(b,h,c1,c2,L,E)
%
% Matriz de rigidez de un elemento columna con nudos rigidos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%---------------------------------------------------------------------------------
% [k]=kcolumnanr(b,h,c1,c2,L,E)
%---------------------------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% L: longitud del elemento.
% E: modulo de elasticidad del material
% beta: factor de forma se considera 1.2
G=0.4*E; beta=1.2; inercia=b*h^3/12; area=b*h; fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-2*fi))/(L*(1+4*fi));
kpf=kf; b=(kf+a)/L; bp=b; t=(b+bp)/L;r=E*area/L
k=zeros(6);
k(1,1)=t; k(1,3)=-(b+c1*t); k(1,4)=-t; k(1,6)=-(bp+c2*t);k(2,2)=r; k(2,5)=-r;
k(3,3)=kf+2*c1*b+c1*c1*t; k(3,4)=b+c1*t; k(3,6)=a+c1*bp+c2*b+c1*c2*t;
k(4,4)=t; k(4,6)=bp+c2*t; k(5,5)=r; k(6,6)=kpf+2*c2*bp+c2*c2*t;
for i=1:5;
for j=i+1:6;
k(j,i)=k(i,j);
end
end
fprintf ('n Matriz de Rigidez de Elemento Columna: nn')
for i=1:6
for j=1:6
fprintf ('%12.3f', k(i,j))
end
fprintf('n')
end
%---fin---
4.2 MATRIZ DE RIGIDEZ DE LA ESTRUCTURA
Se presenta en forma rápida, la forma como se obtiene la matriz de rigidez de una
estructura, orientada al cálculo de la matriz de rigidez lateral. Para el efecto se verá como se
obtiene la matriz de Coordenadas Generalizadas, CG; la matriz que contiene a los Vectores de](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-133-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
123
Colocación, VC, el ensamblaje de la matriz de rigidez de la estructura y finalmente el cálculo de
la matriz de rigidez lateral.
4.2.1 Coordenadas Generalizadas
Para ilustrar el cálculo de la matriz de Coordenadas Generalizadas, CG, en la figura 4.6
se ha dibujado un pórtico de 1 vano y dos pisos. Para el análisis sísmico se considera que
las vigas son axialmente rígidas, de tal forma que se tiene un solo desplazamiento lateral por
piso. Las columnas son totalmente flexibles. Con estas hipótesis se tiene que cada nudo
interior de un pórtico plano tiene dos grados de libertad que son: la componente de
desplazamiento vertical y la rotación. Además en cada piso se tiene un desplazamiento lateral.
Se puede numerar primero los dos grados de libertad de cada nudo interior y al final los
desplazamientos horizontales de piso, así se ha procedido en la figura 4.6. Se pudo también
numerar en primer lugar los desplazamientos horizontales de piso y al final los dos grados de
libertad de cada nudo.
Figura 4.6 Numeración de los nudos y grados de libertad.
A continuación se indica el programa cg, que obtiene los grados de libertad de un
pórtico plano, en el que primero se numeran los dos grados de libertad por nudo
(desplazamiento vertical y giro) y posteriormente el desplazamiento horizontal por piso. La
forma para utilizar el programa es:
[CG]=cg(nod,np,nr)
nod Número de nudos del pórtico plano.
np Número de pisos del pórtico
nr Número de nudos restringidos.
Con esta información de entrada el programa se ejecuta y empieza un dialogo entre el
programa, que hace preguntas y el usuario que suministra los datos.
Con la información del número de nudos, el programa genera una matriz de (nod,3)
llena de 1. El número de filas es igual al número de nudos y el número de columnas es igual a
3, que son los tres grados de libertad que tiene un nudo de un pórtico plano. La primera
columna define el desplazamiento horizontal, la segunda el desplazamiento vertical y la tercera
el giro. A esta matriz se ha denominado CG.
Posteriormente cuando se indica el número de nudos restringidos, se genera un lazo
en que el usuario debe responder, con letra minúscula, si el nudo restringido puede](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-134-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
124
desplazarse horizontalmente, verticalmente o si puede rotar. Para la estructura de la figura 4.6,
las dos primeras filas de la matriz CG que estaban con 1 se cambian por 0. Finalmente en la
última parte del programa se obtienen todos los grados de libertad. En resumen, los valores
que tiene la matriz CG, en cada etapa son:
8
7
10
6
5
10
4
3
9
2
1
9
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
function [CG]=cg(nod,np,nr)
%
% Programa para encontrar las coordenadas generalizadas
% orientado al cálculo de la matriz de rigidez lateral
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [CG]=cg(nod,np.nr)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% nod Número de nudos
% np Número de pisos
% nr Número de nudos restringidos
%
ngl=0; CG=ones(nod,3);
for i=1:np
fprintf ('Nudo mayor del piso, %d ',i)
nn(i)=input (' Numero del nudo:');
end
% análisis de restricciones
for i=1:nr
nudres= input ('n Numero del nudo restringido:');
X1 = input (' Desplazamiento en X ,si(s) o no(n):','s');
if X1=='n'
CG(nudres,1)=0;
else
ngl=ngl+1; CG(nudres,1)=ngl;
end
Y1 = input (' Desplazamiento en Y ,si(s) o no(n):','s');
if Y1=='n'
CG(nudres,2)=0;
else
ngl=ngl+1; CG(nudres,2)=ngl;
end
R1 = input (' Rotacion ,si(s) o no(n):','s');
if R1=='n'
CG(nudres,3)=0;
else
ngl=ngl+1; CG(nudres,3)=ngl;
end](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-135-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
125
end
% grados de libertad
for i=1:nod
for j=1:2
if CG(i,j+1)~=0
ngl=ngl+1; CG(i,j+1)=ngl;
else,end
end
end
ico=0;ii=1;
for i=1:nod-nr
j=nr+i;
if ico==0
ngl=ngl+1; ico=1;
else, end
if j<=nn(ii)
CG(j,1)=ngl;
else,end
if j==nn(ii)
ico=0;ii=ii+1;
else,end
end
% ---end---
En la figura 4.7 se indica la entrada de datos, de la estructura de la figura 4.6, para el
programa CG. Al final se indica lo que reporta el programa. Cada fila de CG contiene la
información de los grados de libertad de un nudo.
>> [CG] = cg (6,2,2)
Nudo mayor del piso, 1 Número del nudo: 4
Nudo mayor del piso, 2 Número del nudo: 6
Número del nudo restringido: 1
Desplazamiento en X, si (s) o no (n): n
Desplazamiento en Y, si (s) o no (n): n
Rotación si (s) o no (n): n
Número del nudo restringido: 2
Desplazamiento en X, si (s) o no (n): n
Desplazamiento en Y, si (s) o no (n): n
Rotación si (s) o no (n): n
CG=
0 0 0
0 0 0
9 1 2
9 3 4
10 5 6
10 7 8
4.2.2 Vector de Colocación
El Vector de Colocación de cada elemento, está conformado por los grados de libertad
del nudo inicial y del nudo final, escritos en el siguiente orden: primero, el desplazamiento
horizontal; segundo, el desplazamiento vertical y tercero, el giro.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-136-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
126
En la figura 4.7, a la izquierda, se indica la numeración de los nudos y a la derecha, de
los elementos de la estructura de 2 pisos y 1 vano. La identificación del nudo inicial y del nudo
final de un elemento, es arbitraria. Sin embargo, se recomienda que en columnas el nudo inicial
sea el que se halla abajo y el nudo final el que se halla arriba; para vigas, se recomienda que el
nudo inicial este a la izquierda y el nudo final a la derecha del elemento. Al aplicar esta
recomendación, se tienen los valores indicados en la tabla 4.1 para la ubicación del nudo inicial
y final.
Figura 4.7 Numeración de nudos y elementos.
function [VC]=vc(mbr,ncol,CG)
%
% Programa para encontrar el vector de colocación de pórticos planos
% orientado al cálculo de la matriz de rigidez lateral
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [VC]=vc(mbr,ncol,CG)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% VC Vector de colocacion
% mbr Número de miembros
% ncol Número de columnas
%
% Información de elementos
for i=1:mbr
if i<=ncol
fprintf ('n Columna %d:',i);
ini(i)=input ('nNumero nudo inicial:');
fin(i)=input ('Numero nudo final:');
else
fprintf ('n viga %d:',i);
ini(i)=input ('nNumero nudo inicial:');
fin(i)=input ('Numero nudo final:');
end
end
% Arreglo VC. Vectores de colocacion
for i=1:mbr
for k=1:3
VC(i,k)= CG(ini(i),k);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-137-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
127
VC(i,k+3) = CG(fin(i),k);
end
end
fprintf(' n Vectores de colocacion de los elementos n')
for i=1:mbr
for k=1:6
fprintf('%7d',VC(i,k))
end
fprintf( 'n')
end
% ---fin---
Tabla 4.1 Identificación del nudo inicial y final de los elementos.
Elemento 1 2 3 4 5 6
Nudo Inicial 1 2 3 4 3 5
Nudo Final 3 4 5 6 4 6
Con la información de la tabla 4.1 y con la matriz de Coordenadas Generalizadas, se
hallan los Vectores de Colocación, que son:
8
7
10
6
5
10
)
6
(
4
3
9
2
1
9
)
5
(
8
7
10
4
3
9
)
4
(
6
5
10
2
1
9
)
3
(
4
3
9
0
0
0
)
2
(
2
1
9
0
0
0
)
1
(
VC
VC
VC
VC
VC
VC
El programa que obtiene el vector de colocación se ha denominado VC y la entrada de
datos es la siguiente:
[VC]=vc(mbr,ncol,CG)
mbr Número de elementos del pórtico.
ncol Número total de columnas.
CG Matriz que contiene las coordenadas generalizadas de cada elemento.
Cuando se ejecuta VC el usuario por pantalla debe indicar al programa el nudo inicial y
el nudo final de cada uno de los elementos de la estructura.
4.2.3 Ensamblaje directo
Una vez que se tiene determinado el Vector de Colocación de cada uno de los
elementos, se procede al cálculo de la matriz de rigidez de la estructura, para lo cual en un
gran lazo que va de 1 al número total de elementos (mbr) se halla la matriz de rigidez del
elemento k , sea este viga o columna. Luego se realiza el ensamblaje utilizando el vector de
colocación como se lo indica en el diagrama de flujo indicado en la figura 4.8. Se ha
denominado SS a la matriz de rigidez de la estructura. En el libro Análisis Matricial de
Estructuras, Aguiar (2004), se presenta el fundamento teórico del ensamblaje directo, con una
serie de ejemplos.
El programa klateral obtiene la matriz de rigidez de la estructura, que se ha visto en
este subapartado y en la última parte del programa determina la matriz de rigidez lateral, que
se estudiará en el próximo apartado. La forma de uso de este programa, es:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-138-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
128
[KL]=klateral(E)
E Es el módulo de elasticidad del material.
Cuando se ejecuta el programa, a más de los datos ya indicados para encontrar las
Coordenadas Generalizadas y el Vector de Colocación, el usuario deberá indicar por pantalla,
la base, la altura de la sección transversal; las longitudes del nudo rígido inicial y final y la luz
libre.
Figura 4.8 Diagrama de flujo para encontrar la matriz de rigidez
function [KL]=klateral(E)
%
% Programa para encontrar la matriz de rigidez lateral de un pórtico plano
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [KL]=klateral(E)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% VC Vector de colocacion
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% long: longitud del elemento.
%
nod=input('n Numero de nudos:');
np=input(' Numero de pisos:');
nr=input(' Numero de nudos restringidos:');
[CG,ngl]=cg1(nod,np,nr);
i=1:mbr
k
i=1:6
jj=VC(i,j)
jj==0 m=1:6
i=1:6
mm=VC(i,m)
mm==0 SS(jj,mm)=SS(jj,mm)+k(j,m)
si
no
si
no](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-139-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
129
mbr=input('nn Numero de miembros:' );
ncol=input('n Numero de columnas:');
[VC]=vc1(mbr,ncol,CG)
for i=1:mbr
if i<=ncol
fprintf ('n Columna %d:',i);
B(i)=input ('n Base:'); H(i)=input ('Altura:'); L(i)=input ('Luz libre:');
C1(i)=input ('Longitud de nudo rigido inicial:');
C2(i)=input ('Longitud de nudo rigido final:');
else
fprintf ('n viga %d:',i);
B(i)=input ('n Base:'); H(i)=input ('Altura:'); L(i)=input ('Luz libre:');
C1(i)=input ('Longitud de nudo rigido inicial:');
C2(i)=input ('Longitud de nudo rigido final:');
end
end
% Calculo de la matriz de rigidez de la estructura
SS=zeros(ngl,ngl);
for i=1:mbr
b=B(i);h=H(i);c1=C1(i);c2=C2(i);long=L(i);
if i<=ncol
[k]=kcnr(b,h,c1,c2,long,E);
else
[k]=kvnr(b,h,c1,c2,long,E);
end
for j=1:6
jj=VC(i,j);
if jj==0
continue
end
for m=1:6
mm=VC(i,m);
if mm==0
continue
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
% Matriz de rigidez lateral
na=ngl-np;nb=np;
Kaa=SS(1:na,1:na);Kab=SS(1:na,na+1:ngl);Kba=Kab';Kbb=SS(na+1:ngl,na+1:ngl);
KL=Kbb-Kba*inv(Kaa)*Kab;
fprintf ('n Matriz de rigidez lateral :')
for i=1,np;
for j=1,np;
fprintf ('%12.3f', KL(i,j))
end
fprintf('n')
end
%---fin---
En el apartado 3.6 se presenta la rutina kvnr que se indica en el programa klateral,
tiene la particularidad de que se usa el artificio, mediante el cual la matriz de rigidez de un
elemento viga es de 6x6 para poder realizar el ensamblaje directo en la forma indicada en el
programa. La otra rutina que se utiliza es kcnr pero esta se obtiene eliminando las
impresiones de la rutina kcolumnanr.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-140-320.jpg)



![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
133
Sea K
+
la matriz de rigidez condensada a las coordenadas "b".
ab
aa
ba
bb K
K
K
K
K 1
(4.11.3)
La ecuación (4.11.3) es la que se utilizó en el programa klateral. En MATLAB como
ya se cuentan con rutinas definidas es muy sencillo determinar las submatrices. El cálculo de la
matriz de rigidez lateral se encuentra en la parte final del programa.
EJEMPLO 4
Encontrar la matriz de rigidez condensada a la coordenada lateral 1, indicada en la
figura 4.10. Que corresponde a la estructura de la figura 4.9, del ejemplo anterior.
SOLUCIÓN
En este caso, la partición de la matriz de rigidez de la estructura K se la realiza en la
primera fila y primera columna, toda vez que existe una sola "coordenada a". Por lo tanto las
submatrices, son:
72
.
1655
0
72
.
1655
0
20
.
2499
ab
aa
K
K
40
.
4497
64
.
658
85
.
80754
17
.
934
64
.
658
40
.
4497
64
.
658
32
.
329
64
.
658
85
.
80754
bb
K
La submatriz Kba es la transpuesta de la submatriz Kab. Para aplicar la ecuación
(4.10.3) es necesario calcular la inversa de Kbb.
5
1
10
27
.
23
1501
.
0
241
.
1
790
.
4
1501
.
0
27
.
23
1501
.
0
0026
.
0
1501
.
0
24
.
1
bb
K
]
772
.
1485
[
*
*
428
.
1013
1
1
K
K
K
K
K
K
K
K
K
ba
bb
ab
aa
ba
bb
ab
4.4 CONDENSACIÓN MEDIANTE SOLUCIÓN DE ECUACIONES
El trabajar con la ecuación (4.10.3) o con la ecuación (4.11.3) implica calcular una
matriz inversa, lo cual demanda bastante tiempo de cálculo, si se piensa en estructuras de
algunos pisos. Razón por la cual, en la práctica, se transforma el cálculo de la matriz inversa
por un sistema de ecuaciones lineales, como se ve a continuación.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-144-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
134
4.4.1 Caso en que Qb = 0
En la ecuación (4.10.3) se realiza, se define la matriz T de la siguiente manera:
ba
bb K
K
T 1
(4.12.1)
Al multiplicar ambos lados de la ecuación (4.12.1) por Kbb, se obtiene:
ba
bb K
T
K
(4.12.2)
Para encontrar la matriz T, se debe resolver un conjunto de ecuaciones lineales, cuya
matriz de coeficientes es la submatriz Kbb y los términos independientes son las diferentes
columnas de la submatriz Kba.
Con el cambio de variable realizado, la ecuación (4.10.3) se transforma en:
T
K
K
K ab
aa
* (4.12.3)
A la matriz se le conoce con el nombre de Matriz de Paso, ya que relaciona dos
sistemas de coordenadas. Aguiar (2004). También se le conoce con el nombre de Matriz de
Incidencia.
EJEMPLO 5
Encontrar la matriz de rigidez condensada del ejercicio anterior, por intermedio de la
matriz T.
SOLUCIÓN
Al sustituir las submatrices, del ejemplo anterior en (4.12.2), se obtiene:
72
.
1655
0
72
.
1655
0
40
.
4497
64
.
658
17
.
934
64
.
658
64
.
658
85
.
80754
64
.
658
32
.
329
17
.
934
64
.
658
40
.
4497
64
.
658
64
.
658
32
.
329
64
.
658
85
.
80754
41
31
21
11
T
T
T
T
La solución del sistema de ecuaciones lineales, reporta
30599
.
0
00497
.
0
30605
.
0
00497
.
0
T
]
772
.
1485
[
*
*
]
428
.
1013
[
K
T
K
K
K
T
K
ab
aa
ab](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-145-320.jpg)







![SISTEMAS DE UN GRADO DE LIBERTAD
142
Matriz de rigidez lateral
492
.
5358
309
.
3509
309
.
3509
582
.
4516
15
.
8013
15
.
8013
15
.
8013
30
.
16026
1
ba
bb
ab
aa K
K
K
K
658
.
2654
841
.
4503
841
.
4503
718
.
11509
L
K
Se han presentado dos modelos para el cálculo de la matriz de rigidez lateral, el
primero es más adecuado pero demanda de una mayor cantidad de números. En estructuras
esbeltas es necesario considerar la deformación axial en los elementos, si la relación alto-
ancho en planta, es mayor que tres se debe considerar la deformación axial.
En el programa klateral se utilizan dos rutinas que no han sido indicadas la una es la
que obtiene la matriz de rigidez de elemento, en vigas, denominada kvnr y la otra la que
obtiene la matriz de rigidez de elemento, en columnas. En el ensamblaje de la matriz de rigidez
que se utiliza en el programa klateral, se trabaja con matrices de 6 x 6 para los elementos pero
al considerar que la viga es axialmente rígida, esta matriz es de 4 x 4 razón por la cual se
utiliza un artificio en el programa kvnr para que sea de 6 x 6.
Figura 4.18 Significado físico de los elementos de la primera columna de la matriz de rigidez, para el
primer modelo de cálculo.
En la figura 4.18 se indica el significado físico de los elementos de la primera columna
de la matriz de rigidez lateral, para el primer modelo de cálculo. Se aprecia que son las fuerzas
que producen un desplazamiento unitario en el primer piso y nulo en el segundo piso.
function [k]=kvnr(b,h,c1,c2,L,E)
%
% Matriz de rigidez de un elemento viga con nudos rígidos
% Se usa para el cálculo de la matriz de rigidez de la estructura
% Se la completa a 6X6 con ceros en la primera y cuarta fila.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%--------------------------------------------------------------------
% [k]=kvnr(b,h,c1,c2,L,E)
%--------------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% c1 longitud del nudo rígido en el nudo inicial.
% c2 longitud del nudo rígido en el nudo final.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-153-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
144
Figura 4.19 Pila de un Puente y modelo para el análisis sísmico.
SOLUCIÓN
En la figura 4.20 se presenta el modelo de cálculo con nudos rígidos. La línea de la
mitad representan los ejes de cada uno de los elementos y las partes más negreadas los nudos
rígidos; se indica los valores de y . La Pila del Puente está empotrada en la cimentación,
razón por la cual para determinar el valor de en el nudo inicial se supone que existe una viga
de las mismas dimensiones de la viga superior.
Figura 4.20 Modelo de análisis con nudos rígidos.
La matriz de rigidez de la viga izquierda que se halla con la ecuación (4.5), en la que se
tiene es la siguiente:
[ ]
A la longitud del elemento se ha denominado luz libre. Para la viga derecha los
valores son: Más abajo se indica esta matriz de rigidez.
Para la Pila se trabaja con la ecuación matricial indicada en la ecuación (4.5). En este
caso los valores son: La matriz que se obtiene es:
C1= 0
C2= 1.0 C1= 1.0
C2= 0
C1= 0.6
C2= 0.6
3.40
4.00 4.00
LL=
LL= LL=](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-155-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
145
[ ]
No se ha colocado decimales en la matriz de rigidez del elemento 3. La matriz de
rigidez de la estructura se halla por ensamblaje directo. Cuando se realiza el ensamblaje a
mano es conveniente colocar los vectores de colocación en la parte superior de la matriz de
rigidez del elemento y a la derecha.
Se deja al lector la realización del ensamblaje y la verificación de los resultados que se
indican más adelante. De igual forma la obtención de las sub matrices con las cuales se
obtiene la matriz de rigidez condensada, la misma que vale 48659.17 T/m.
Elemento 1
Elemento 2
Elemento 3
Matriz de rigidez de la estructura
Ahora, se resuelve el problema, utilizando el programa de CEINCI-LAB denominado:
krigidez_nudo_rigido que encuentra la matriz de rigidez por ensamblaje directo. Este
programa llama al programa kmiembro_nudo_rigido. El usuario debe elaborar su propio
programa de ordenador e indicar los datos que requieren los programas que va a utilizar.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-156-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
146
A continuación se indica el listado del programa que se ha elaborado para calcular la
matriz de rigidez lateral de la estructura de la figura 4.19. Los resultados han sido ya
presentados.
% Programa para calcular matriz de rigidez para análisis sísmico de %
% una Pila de un Puente considerando nudos rígidos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%--------------------------------------------------------------
ngl=7; % Número de grados de libertad
VC=[1 2 3 1 4 5; 1 4 5 1 6 7; 0 0 0 1 4 5];
L=[4.0; 4.0; 3.40]; % Luz Libre
cc1=[0; 1; 0.6]; % Nudo rígido Nudo Inicial
cc2=[1; 0; 0.6]; % Nudo rígido Nudo Final
seno=[0; 0; 1]; coseno=[1; 1; 0];
ELEM=[0.80 1.20; 0.80 1.20; 1.0 2.0];
E=1800000; % Modulo de Elasticidad
[SS]=krigidez_nudo_rigido(ngl,ELEM,cc1,cc2,L,seno,coseno,VC,E)
Kaa=SS(1,1); Kab=SS(1,2:7); Kbb=SS(2:7,2:7);Kba=Kab';
K=Kaa-Kab*inv(Kbb)*Kba % Matriz de rigidez en coordenadas principales
%end
Programa krigidez_nudo_rigido
function
[SS]=krigidez_nudo_rigido(ngl,ELEM,cc1,cc2,L,seno,coseno,VC,E)
%
% Programa para encontrar la matriz de rigidez de un pórtico plano
% o de una Armadura Plana
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [SS]=krigidez_nudo_rigido(ngl,ELEM,cc1,cc2,L,seno,coseno,VC,E)
%-------------------------------------------------------------
% ELEM Matriz que contiene la base y la altura de los elementos
% para el caso de pórticos planos.
% ELEM Vector que contiene el área de los elementos de armadura
% cc1 Vector con longitud del nudo final de cada elemento.
% cc2 Vector con longitud del nudo final de cada elemento
% L Vector que contiene la luz libre de los elementos
% seno Vector que contiene los senos de los elementos
% coseno Vector que contiene los cosenos de los elementos
% VC Matriz que contiene los vectores de colocación de elementos
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% ngl Número de grados de libertad
%
mbr=length(L); SS=zeros(ngl);icod=length(VC(1,:));
for i=1:mbr
if icod==4
A=ELEM(i,1); %Area de elemento
Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kdiagonal(A,Lon,E,sen,cose);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-157-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
147
else
b=ELEM(i,1);h=ELEM(i,2);Lon=L(i);sen=seno(i);cose=coseno(i);
c1=cc1(i); % Longitud de nudo rigido de nudo inicial.
c2=cc2(i); % Longitud de nudo rigido de nudo final.
[k]=kmiembro_nudo_rigido (b,h,c1,c2,Lon,E,sen,cose);
end
for j=1:icod
jj=VC(i,j);
if jj==0
continue
end
for m=1:icod
mm=VC(i,m);
if mm==0
continue
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
return
%---fin---
Programa kmiembro_nudo_rigido
function [K3]=kmiembro_nudo_rigido(b,h,c1,c2,L,E,seno,coseno)
%
% Matriz de rigidez de un elemento en coordenadas globales
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [K3]=kmiembro_nudo_rigido(b,h,c1,c2,L,E,seno,coseno)
%-------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% c1: Longitud de nudo rígido del Nudo Inicial.
% c2: Longitud de nudo rígido de Nudo Final.
% L: longitud del elemento.
% E: modulo de elasticidad del material
% seno: seno del elemento para pasar de local a global
% coseno: coseno del elemento para pasar de local a global
G=840000; beta=1.2; inercia=b*h^3/12; area=b*h;
fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-
2*fi))/(L*(1+4*fi));
b=(kf+a)/L; t=2*b/L; r=E*area/L;
if seno==0 % caso de viga
K3=[0 0 0 0 0 0;
0 t b+c1*t 0 -t b+c2*t;
0 b+c1*t kf+2*c1*b+c1^2*t 0 -(b+c1*t) a+c1*b+c2*b+c1*c2*t;
0 0 0 0 0 0;
0 -t -(b+c1*t) 0 t -(b+c2*t);
0 b+c2*t a+c1*b+c2*b+c1*c2*t 0 -(b+c2*t) kf+2*c2*b+c2^2*t];
else
K3=[t 0 -(b+c1*t) -t 0 -(b+c2*t);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-158-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
148
0 r 0 0 -r 0;
-(b+c1*t) 0 kf+2*c1*b+c1^2*t b+c1*t 0 a+c1*b+c2*b+c1*c2*t;
-t 0 b+c1*t t 0 b+c2*t;
0 -r 0 0 r 0;
-(b+c2*t) 0 a+c1*b+c2*b+c1*c2*t b+c2*t 0 kf+2*c2*b+c2^2*t];
end
return
%---fin---
EJEMPLO 10
Los dos primeros pisos, de la estructura, presentada a la izquierda, de la figura 4.21,
son de hormigón armado, compuesto por columnas de 30/80 cm., y vigas de 30/70 cm., con un
módulo de elasticidad de 1800000 T/m
2
. El tercer piso es de acero de lamina delgada
conformada por 2 perfiles doble “G” de 200/50/10/3 mm. , cuya sección se indica en la parte
derecha de la figura 4.21.
Figura 4.21 Estructura mixta de hormigón y acero.
Figura 4.22 Modelo de análisis sísmico y grados de libertad.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-159-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
149
Para el análisis sísmico las masas se han concentrado en los nudos y se ha
considerado que las vigas son axialmente rígidas. Se pide realizar un programa de
computación, utilizando la librería de programas de CEINCI-LAB y presentar la matriz de
rigidez asociada a las coordenadas laterales de piso.
SOLUCIÓN
El momento de inercia de las dos vigas de acero doble “G” es ; y el
área es . Como se va a trabajar en T. y m.; la inercia y área anotados se debe
transformar a y , respectivamente: El módulo de elasticidad del acero .
% Programa para realizar el análisis sísmico de estructura
% con dos pisos de hormigón armado y tercer piso de acero.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Mayo de 2011
%--------------------------------------------------------------
ngl=15; % Número de grados de libertad
%--------------Hormigón Armado-----------------------
VCH=[0 0 0 1 4 5; 0 0 0 1 6 7; 1 4 5 2 8 9; 1 6 7 2 10 11;
1 4 5 1 6 7; 2 8 9 2 10 11];
LH=[2.9; 2.9; 2.9; 2.9; 5.7; 5.7];
senoH=[1; 1; 1; 1; 0; 0];
cosenoH=[0; 0; 0; 0; 1; 1];
ELEMH=[0.3 0.8;0.3 0.8;0.3 0.8;0.3 0.8;0.3 0.7;0.3 0.7];
EH=1800000; % Modulo de elasticidad del Hormigón
[SH]=krigidez(ngl,ELEMH,LH,senoH,cosenoH,VCH,EH);% K elemen. Hormigón
%--------------Acero---------------------------------------
VCA=[2 8 9 3 12 13; 2 10 11 3 14 15;3 12 13 3 14 15];
LA=[2.9; 2.9; 5.7];
senoA=[1; 1; 0]; cosenoA=[0; 0; 1];A=0.001801; Ix=0.0000097468;
ELEMA=[A Ix; A Ix; A Ix];
EA=21000000; % Modulo de elasticidad del Acero
[SA]=krigidez_acero(ngl,ELEMA,LA,senoA,cosenoA,VCA,EA); % K Acero
%------------------------------------------------------------
S=SH+SA; % Matriz de rigidez Acero y Hormigón
Kaa=S(1:3,1:3); Kab=S(1:3,4:15); Kbb=S(4:15,4:15);Kba=Kab';
K=Kaa-Kab*inv(Kbb)*Kba % Matriz de rigidez en coordenadas principales
%end
La matriz de rigidez, asociada a las coordenadas principales, indicadas a la derecha de
la figura 4.22, es.
[ ]
Programa krigidez
function [SS]=krigidez(ngl,ELEM,L,seno,coseno,VC,E)
%
% Programa para encontrar la matriz de rigidez de un pórtico plano
% O de una Armadura Plana
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-160-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
150
% Octubre de 2009 Primera Versión
% Noviembre de 2009 Segunda Versión (Se incorpora armadura)
%-------------------------------------------------------------
% ELEM Matriz que contiene la base y la altura de los elementos
% para el caso de pórticos planos.
% ELEM Vector que contiene el área de los elementos de armadura
% L Vector que contiene la longitud de los elementos
% seno Vector que contiene los senos de los elementos
% coseno Vector que contiene los cosenos de los elementos
% VC Matriz que contiene los vectores de colocación de elementos
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% ngl Número de grados de libertad
%
mbr=length(L); SS=zeros(ngl);icod=length(VC(1,:));
for i=1:mbr
if icod==4
A=ELEM(i,1); %Area de elemento
Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kdiagonal(A,Lon,E,sen,cose);
else
b=ELEM(i,1);h=ELEM(i,2);Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kmiembro(b,h,Lon,E,sen,cose);
end
for j=1:icod
jj=VC(i,j);
if jj==0
continue
end
for m=1:icod
mm=VC(i,m);
if mm==0
continue
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
return
%---fin---
Programa kmiembro
function [K3]=kmiembro(b,h,L,E,seno,coseno)
%
% Matriz de rigidez de un elemento en coordenadas globales
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Octubre de 2009
%-------------------------------------------------------------
% [K3]=kmiembro(b,h,L,E,seno,coseno)
%-------------------------------------------------------------
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% L: longitud del elemento.
% E: modulo de elasticidad del material](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-161-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
151
% seno: seno del elemento para pasar de local a global
% coseno: coseno del elemento para pasar de local a global
G=840000; beta=1.2; inercia=b*h^3/12; area=b*h;
fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-
2*fi))/(L*(1+4*fi));
kpf=kf; r=E*area/L;
K1=[kf a 0; a kpf 0; 0 0 r];% Matriz de rigidez en
sistema uno
T12=[0 1/L 1 0 -1/L 0;% Matriz de paso de sistema 1 a sistema 2
0 1/L 0 0 -1/L 1;% Sistema 2 son coordenadas locales
-1 0 0 1 0 0];
K2=T12'*K1*T12;% Matriz de rigidez en coordenadas locales
T23=zeros(6,6);T23(1,1)=coseno;T23(2,2)=coseno;T23(3,3)=1;T23(4,4)=cos
eno;
T23(5,5)=coseno;T23(6,6)=1;T23(2,1)=-seno;T23(1,2)=seno;T23(5,4)=-
seno;T23(4,5)=seno;
K3=T23'*K2*T23;
return
%---fin---
Programa krigidez_acero
function [SS]=krigidez_acero(ngl,ELEM,L,seno,coseno,VC,E)
%
% Programa para encontrar la contribución de vigas de acero
% a la matriz de rigidez.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Enero de 2010
%-------------------------------------------------------------
% [SS]=krigidez_acero(ngl,ELEM,L,seno,coseno,VC,E)
%-------------------------------------------------------------
% ELEM Matriz que contiene el área e inercia de los elementos
% L Vector que contiene la longitud de los elementos
% seno Vector que contiene los senos de los elementos
% coseno Vector que contiene los cosenos de los elementos
% VC Matriz que contiene los vectores de colocación de elementos
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% ngl Número de grados de libertad
%
mbr=length(ELEM(:,1))
SS=zeros(ngl);
for i=1:mbr
area=ELEM(i,1);iner=ELEM(i,2);Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kmiembro_acero(area,iner,Lon,E,sen,cose);
for j=1:6
jj=VC(i,j);
if jj==0
continue
end
for m=1:6
mm=VC(i,m);
if mm==0
continue](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-162-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
152
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
return
%---fin---
Programa kmiembro_acero
function [K3]=kmiembro_acero(area,inercia,L,E,seno,coseno)
%
% Matriz de rigidez de un elemento en coordenadas globales
% son datos el ares y la inercia del elemento
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Enero de 2010
%-------------------------------------------------------------
% [K3]=kmiembro(area,iner,L,E,seno,coseno)
%-------------------------------------------------------------
% area: area de la seccion transversal.
% iner: inercia de la seccion transversal.
% L: longitud del elemento.
% E: modulo de elasticidad del material
% seno: seno del elemento para pasar de local a global
% coseno: coseno del elemento para pasar de local a global
G=0.4*E; beta=1.2; fi=(3*E*inercia*beta)/(G*area*L*L);
kf=((4*E*inercia)*(1+fi))/(L*(1+4*fi)); a=((2*E*inercia)*(1-
2*fi))/(L*(1+4*fi));
kpf=kf; r=E*area/L;
K1=[kf a 0; a kpf 0; 0 0 r];% Matriz de rigidez en
sistema uno
T12=[0 1/L 1 0 -1/L 0;% Matriz de paso de sistema 1 a sistema 2
0 1/L 0 0 -1/L 1;% Sistema 2 son coordenadas locales
-1 0 0 1 0 0];
K2=T12'*K1*T12;% Matriz de rigidez en coordenadas locales
T23=zeros(6,6);T23(1,1)=coseno;T23(2,2)=coseno;T23(3,3)=1;T23(4,4)=cos
eno;
T23(5,5)=coseno;T23(6,6)=1;T23(2,1)=-seno;T23(1,2)=seno;T23(5,4)=-
seno;T23(4,5)=seno;
K3=T23'*K2*T23;
return
%---fin---
Se ha trabajado con un modelo aproximado para el acero ya que se ha considerado los
giros, se deja al lector calcular con otro modelo que no considere los giros en el tercer piso; la
matriz de rigidez va a cambiar muy poco.
4.8 PROGRAMA rlaxinfi
El programa reporta la matriz de rigidez lateral en pórticos planos de hormigón
armado y que sean completamente regulares en elevación. La matriz de rigidez lateral se
graba en consola con el nombre de KL para que se pueda utilizar en otros cálculos. La
forma de uso del programa es:
[KL] = rlaxinfi (Nombre)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-163-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
153
Nombre. Es el nombre del archivo que contiene la base y la altura de la sección
transversal y la longitud de los elementos.
function[KL]=rlaxinfi(nombre)
%
% Programa para encontrar la matriz de rigidez lateral de un pórtico plano
% considerando que todos los elementos son axialmente rigidos.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [KL]=rlaxinfi(nombre)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% VC Vector de colocacion
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% long: longitud del elemento.
% nombre Archivo de datos que contiene la base, la altura y la longitud
% de cada uno de los elementos.
%
nod=input('n Numero de nudos:');
np=input(' Numero de pisos:');
nr=input(' Numero de nudos restringidos:');
E=input(' Modulo de elasticidad:');
% Coordenadas Generalizadas
CG=zeros(nod,2);ngl=0;k=nr;
for i=1:np
ngl=ngl+1;
for j=1:nr
k=k+1; CG(k,1)=ngl;
end
end
for i=1:nod-nr
ngl=ngl+1;
k=nr+i; CG(k,2)=ngl;
end
ncol=np*nr; mbr=ncol+(nr-1)*np;nvig=mbr-ncol;
ici=0;icf=nr;
for i=1:ncol
ici=ici+1; icf=icf+1;ini(i)=ici;fin(i)=icf;
end
ii=ncol;
for j=1:np
ici=j*nr;
for i=1:nr-1
ii=ii+1;ici=ici+1;ini(ii)=ici;fin(ii)=ici+1;
end
end
% Arreglo VC. Vectores de colocacion
for i=1:mbr
for k=1:2
VC(i,k)= CG(ini(i),k);
VC(i,k+2) = CG(fin(i),k);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-164-320.jpg)


![SISTEMAS DE UN GRADO DE LIBERTAD
156
>> casa=[0.4 0.4 3.0;
0.4 0.4 3.0;
0.4 0.4 3.0;
0.4 0.4 3.0;
0.4 0 .4 3.0;
0.0001 0.0001 3.0;
0.3 0.3 4.0;
0.3 0.3 4.0;
0.3 0.3 4.0;
0.0001 0.0001 4.0]
>> load c:casa
>> [KL]=rlaxinfi(casa)
Número de nudos: 9
Número de pisos: 2
Número de nudos restringidos: 3
Módulo de Elasticidad: 2100000
Cálculo con Inercias Gruesas, Código = 0. Con Inercias Agrietadas, Código = 1
Ingrese Código de Inercias=0
PROGRAMA REPORTA
2
.
1257
3
.
2047
3
.
2047
4
.
6405
KL
Al calcular con Inercias Agrietadas, se halla:
4
.
831
0
.
1487
0
.
1487
2
.
4804
KL
El NEC-11 contempla las siguientes inercias agrietadas: g
V I
I 5
.
0
; g
C I
I 8
.
0
.
Donde g
I es la inercia gruesa.
4.9 MATRIZ DE RIGIDEZ DE ELEMENTO MAMPOSTERÍA
En el Ecuador se construyen las columnas dejando unos chicotes, que son hierros de 8
mm de diámetro que sobresalen de la columna unos 40 o 50 cm.; cada 30 o 40 cm., de alto.
Posteriormente se coloca la mampostería y los chicotes quedan en la mitad del mortero
horizontal utilizado para pegar la mampostería.
También se acostumbra primero construir la mampostería dejando entrantes y salientes
en el sitio donde van las columnas de hormigón armado, de esta manera la pared se convierte
en encofrado ya que cuando se vierte el hormigón, una parte va a la mampostería.
En los dos casos la mampostería se está acoplando a la estructura y es fundamental
considerarla en el análisis, no hacerlo puede ser peligroso en estructuras que tienen una mala
distribución de las paredes (no colocadas en forma simétrica).
En la parte superior izquierda de la figura de 4.25, se presenta un pórtico con
mampostería acoplada a las columnas; en la parte superior derecha se aprecia el ancho
equivalente a del puntal equivalente con que se modela la mampostería que trabaja a](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-167-320.jpg)



![SISTEMAS DE UN GRADO DE LIBERTAD
160
Matriz de rigidez completa
9
.
683
4
.
99
9
.
259
4
.
99
9
.
683
9
.
259
9
.
259
9
.
259
1
.
4254
K
Submatrices
9
.
683
4
.
99
4
.
99
9
.
683
9
.
259
9
.
259
1
.
4254 BB
t
AB
BA
AB
AA K
K
K
K
K
Matriz de rigidez lateral
6
.
4081
L
K
En la figura 4.28 se presenta, los valores de la matriz de rigidez lateral que se halla,
con nueve modelos, para encontrar el ancho del puntal equivalente, se deja al lector que saque
sus propias conclusiones con los diferentes resultados.
Figura 4.28 Matriz de rigidez lateral encontrada con nueve modelos.
4.10 PROGRAMA rlaxinfimamposteria
La forma de uso del programa rlaxinfimamposteria es muy similar al del programa
rlaxinfi. Debido a que se debe crear un archivo de datos con la siguiente información:
Base, altura y longitud de todas las columnas y de todas las vigas. En este orden.
Se debe indicar el nudo inicial, el nudo final y la longitud de la diagonal equivalente.
Por pantalla, se suministra información complementaria como el número de nudos,
número de pisos, módulos de elasticidad del hormigón y de la mampostería, etc.
0
1000
2000
3000
4000
5000
6000
0 1 2 3 4 5 6 7 8 9 10
Modelo Matemático
Rigidez
Lateral
del
Pórtico
[Tn/m]
1. Holmes (1961)
2. Mainstone (1971)
3. Bazan (1980)
4. Hendry (1981)
5. Liauw y Kw an (1984)
6. Decanini y Fantin (1986)
7. Paulay y Priestley (1992)
8. FEMA (1997)
9. Crisafulli (1997)
Valor Medio](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-171-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
161
El ancho de la diagonal equivalente se halla con el modelo de Paulay y Priestley (1992)
que ha sido acogido por la norma de Albañilería del Perú E 070.
function[KL]=rlaxinfimamposteria(nombre)
%
% Programa para encontrar la matriz de rigidez lateral de un pórtico plano
% considerando que todos los elementos son axialmente rigidos.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Incorporación de Mampostería en Noviembre de 2007
%
%-------------------------------------------------------------
% [KL]=rlaxinfimamposteria(nombre)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% VC Vector de colocacion
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% b: base de la seccion transversal.
% h: altura de la seccion transversal.
% long: longitud del elemento.
% t: espesor de la mampostería
% nombre Archivo de datos que contiene la base, la altura y la longitud
% de cada uno de los elementos. El nombre debe tener extensión .tex.
% Esto para columnas y vigas. Después para la mampostería se debe
% indicar el nudo inicial, el final y la longitud de la diagonal.
%
% Se considera el modelo de la Norma de Perú para el ancho
% equivalente de la mampostería.
%
nod=input('n Numero de nudos:');
np=input(' Numero de pisos:');
nr=input(' Numero de nudos restringidos:');
nd=input(' Numero de diagonales de mamposteria:');
E=input(' Modulo de elasticidad de Hormigon (T/m2):');
Em=input(' Modulo de elasticidad de Mamposteria (T/m2):');
t=input(' Espesor de la Mamposteria (m):');
% Coordenadas Generalizadas
CG=zeros(nod,2);ngl=0;k=nr;
for i=1:np
ngl=ngl+1;
for j=1:nr
k=k+1; CG(k,1)=ngl;
end
end
for i=1:nod-nr
ngl=ngl+1;
k=nr+i; CG(k,2)=ngl;
end
ncol=np*nr; mbr=ncol+(nr-1)*np;nvig=mbr-ncol;
ici=0;icf=nr;
for i=1:ncol
ici=ici+1; icf=icf+1;ini(i)=ici;fin(i)=icf;
end
ii=ncol;
for j=1:np](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-172-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
163
continue
end
for m=1:4
mm=VC(i,m);
if mm==0
continue
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
% Matriz de rigidez lateral
na=np;nb=ngl-np;
Kaa=SS(1:na,1:na);Kab=SS(1:na,na+1:ngl);Kba=Kab';Kbb=SS(na+1:ngl,na+1:ngl);
KL=Kaa-Kab*inv(Kbb)*Kba;
fprintf ('n Matriz de rigidez lateral :');
save c:KL
%---fin---
EJEMPLO 13
Presentar el archivo de datos, para hallar la matriz de rigidez lateral del pórtico,
presentado a la izquierda de la figura 4.29. Todas las vigas y columnas son de 30/40 cm., el
ancho de la pared es de 20 cm. El módulo de elasticidad del hormigón es 1500000 T/m
2
y el
módulo de elasticidad de la mampostería es 100000 T/m
2
. Ilustrar la forma de uso del programa
rlaxinfimamposteria
Figura 4.29 Estructura con mampostería acoplada y numeración de nudos y elementos
SOLUCIÓN
>> casa_mamposteria=[.3 .4 3.2;.3 .4 3.2;.3 .4 3.2;.3 .4 3.2;.3 .4
5;.3 .4 5;1 4 5.49;3 6 5.38]
casa_mamposteria =
0.3000 0.4000 3.2000](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-174-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
164
0.3000 0.4000 3.2000
0.3000 0.4000 3.2000
0.3000 0.4000 3.2000
0.3000 0.4000 5.0000
0.3000 0.4000 5.0000
1.0000 4.0000 5.4900
3.0000 6.0000 5.3800
>> [KL]=rlaxinfimamposteria(casa_mamposteria)
Numero de nudos:6
Numero de pisos:2
Numero de nudos restringuidos:2
Numero de diagonales de mamposteria:2
Modulo de elasticidad de Hormigón (T/m2):1500000
Modulo de elasticidad de Mampostería (T/m2):100000
Espesor de la Mampostería (m):.20
Calcula con: Inercias gruesas, código=0. Con inercias agrietadas, código=1
Ingrese código de inercias :0
Para diagonal equivalente i= 7
Ingrese la distancia horizontal de mampostería: 4.6
Para diagonal equivalente i=8
Ingrese la distancia horizontal de mampostería: 4.6
Con el último dato se halla el
Cos dividiendo este valor para la longitud de la diagonal
equivalente; con esto se halla la matriz de rigidez en coordenadas globales.
* +
REFERENCIAS
1. Aguiar R., (2004), Análisis Matricial de Estructuras, Centro de Investigaciones
Científicas. Politécnica del Ejército. Segunda edición, 550 p., Quito.
2. Bazán E., and Meli R., (1980), “Seismic analysis of structures with masonry walls”,
Proceedings of the Seventh World Conference on Earthquake Engineering, Vol. 5, 633-
640, Istanbul, Turkey.
3. Carrillo C., (2008), Comparación de la respuesta sísmica incorporando y desacoplando
la mampostería y técnicas de reforzamiento, Tesis de Pregrado en Ing. Civil.
Politécnica del Ejército, 200 p., Quito.
4. Crisafulli F., (1997), Seismic behaviour of reinforced concrete structures with masonry
infills, A thesis submitted in partial fulfillment of the requirements for the degree of
Doctor of Philosophy in Civil Engineering, University of Canterbury, 404 p.,
Christchurch, New Zealand.
5. Decanini L., y Fantin G., (1986), “Modelos simplificados de la mampostería incluida en
pórticos. Carácteristicas de rigidez y resistencia lateral en estado limite” Jornadas
Argentinas de Ingeniería Estructural, Vol 2, 817-836, Buenos Aires, Argentina.
6. Holmes M., (1961), “Steel frames with brickwork and concrete infilling”, Proceedings of
the Institution of Civil Engineers, Vol. 19, 473-478.
7. Liauw T., and Kwan K., (1984), “Nonlinear behaviour of non-integral infilled frames”,
Computers & Structures, 18 (3), 551-560.
8. Mainstone R., (1971), “On the stiffnesses and strengths of infilled frames”, Proceedings
of the Institution of Civil Engineers, Supplement IV, 57-90.
9. Paulay T., and Priestley M., (1992), Seismic design of reinforced concrete and masonry
buildings, John Wiley & Sons Inc, 744 p.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-175-320.jpg)
















![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
181
̇ ̇ ̇ ̇ ̇ ̇ ̇ ̇
Figura 5.16 Modelo de análisis Plano de Interacción suelo-estructura.
Figura 5.17 Deformada General.
Al desarrollar la expresión indicada, sacar factor común y al aplicar la regla indicada para
encontrar la matriz de masas, se encuentra.
[ ]
(5.11)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-192-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
183
Figura 5.19 Estructura de Ejemplo 4, considerando interacción suelo estructura.
Figura 5.20 Modelo numérico y grados de libertad.
En general la matriz de rigidez, para el caso plano, en que se considera la interacción
suelo-estructura tiene la siguiente forma. Aguiar (1991).
[ ]
(5.12)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-194-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
185
√
( )
( )
* +
[ ]
[ ]
5.9 AISLADORES DE BASE
En el mega sismo de Chile de 2010, las estructuras con aisladores de base o con
disipadores de energía tuvieron un excelente comportamiento sísmico lo que ha motivado un
incremento notable de las construcciones con estos dispositivos de control pasivo, en Chile. En
el Ecuador todavía no despeja la construcción de edificios con aisladores de base; se han
construido varios puentes con aisladores FPS (Frictional Pendulum System) en el estuario del
río Esmeraldas y en Bahía de Caráquez. Aguiar et al. (2010).
En la figura 5.22 se tiene una estructura de un vano y un piso sobre aisladores de base
elastoméricos (goma-acero-goma-acero….). Se ha denominado , a la rigidez,
amortiguamiento y masa del sistema de aislamiento, , , , a la rigidez, amortiguamiento y
masa de la estructura (con base empotrada) que en los libros de aislación sísmica se denomina
superestructura. Aguiar et al. (2008).
En la figura 5.22 se aprecia que los aisladores de base se han colocado debajo de una
losa de piso y están sobre la cimentación, la misma que puede ser: plintos, viga o losa de
cimentación.
Los aisladores se deforman en la forma indicada a la derecha de la figura 5.22, trabajan
al corte, pero mueven a la superestructura como cuerpo rígido, de tal manera que todo el
sistema se desplaza , como se aprecia a la izquierda de la figura 5.22. La superestructura se
deforma el mismo que se mide con relación al desplazamiento](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-196-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
186
Figura 5.22 Nomenclatura y coordenadas relativas.
5.9.1 Matriz de Masas
La energía cinética del sistema estructural indicado en la figura 5.22, es la siguiente:
̇ ̇ ̇
Luego:
[ ̇ ̇ ̇ ̇ ]
De donde:
* +
5.9.2 Matriz de Rigidez y Amortiguamiento
La matriz de rigidez que se presentó para el caso de interacción suelo estructura,
ecuación (5.12) es diagonal, en la que en primer lugar se ha numerado los grados de libertad
de la estructura y después de la cimentación. Ahora si en ese modelo, no se considera el
resorte rotacional y además primero se numera el desplazamiento de la cimentación y luego
de la estructura, como se indica en la figura 5.23, la matriz de rigidez es:
[ ]
Donde es la rigidez del resorte traslacional; es la matriz de rigidez de la
estructura con base empotrada. El modelo indicado en la figura 5.23, corresponde también al
de aislación sísmica por lo que al trabajar con coordenadas relativas, su matriz de rigidez es:
[ ]
Siendo la rigidez del sistema de aislación y la matriz de rigidez de la
superestructura obtenida con base empotrada.
(5.17)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-197-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
187
Figura 5.23 Similitud con modelo de aislación sísmica
Se deja al lector que demuestre que la matriz de masas del sistema indicado en la
figura 5.23 es.
[ ]
En base a la matriz de masas presentada y a la indicada en el apartado anterior, el
lector puede generalizar está matriz para el caso plano, de estructuras con aisladores de base,
solamente debe tener en cuenta que .
La matriz de amortiguamiento se verá con detenimiento en el capítulo 7, sin embargo
para aprovechar el tema que se está tratando se presenta a continuación, la matriz de
amortiguamiento para el modelo numérico indicado en la figura 5.22.
[ ]
5.9.3 Ecuación diferencial del movimiento
En la figura 5.24 se ha vuelto a presentar el modelo de 2 grados de libertad indicado en
la figura 5.22, para tenerlo presente, ya que en este apartado se indica a continuación el
sistema de ecuaciones diferenciales de ese modelo numérico de cálculo, con el propósito de
entender un poco más el comportamiento de estructuras con aisladores de base.
La ecuación diferencial que gobierna el comportamiento de las estructuras con
aisladores de base elastoméricos, es la siguiente.
̈ ̇
Donde ,son las matrices de masa, amortiguamiento y rigidez de la estructura con
aisladores de base; ̇ ̈ , son los vectores de desplazamiento, velocidad y aceleración; es el
vector que relaciona el movimiento del suelo con los grados de libertad de la estructura, para el
caso de análisis sísmico en sentido horizontal y para el sistema de 2 grados de libertad, que se
está analizando, el vector vale 1 y 0; es la aceleración del suelo.
kd
m1
m2
mo
m1
m2
mo
q1
q2
q3
q1
q2
q3
(5.18)
(5.19)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-198-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
188
Figura 5.24 Sistema de dos grados de libertad.
Al reemplazar las matrices de masa, amortiguamiento y rigidez, del sistema de 2
grados de libertad, indicado en la figura 5.24, en la ecuación diferencial del movimiento, se
halla.
* + [
̈
̈
] [ ] [
̇
̇
] [ ] * + * + * +
Al desarrollar el sistema de ecuaciones diferenciales se encuentra.
̈ ̈ ̇
̈ ̈ ̇
Ahora lo que interesa ilustrar es como se obtiene para ello se denomina masa total
del sistema a:
Al trabajar solo con la primera ecuación diferencial se tiene:
̈ ̇ ̈
Como aproximación se considera que ̈ . Luego la ecuación diferencial queda.
̈ ̇
Que corresponde a un sistema de un grado de libertad con masa total . En un
sistema de 1 gdl., se sabe que:
√
Pero la frecuencia natural . Donde es el período objetivo del sistema de
aislación. Luego:
( )
(5.20)
(5.21)
(5.22)
(5.23)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-199-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
190
[ ]
La matriz de rigidez se obtuvo con el programa rlaxinfi, visto en el capítulo anterior y
es la siguiente.
[ ]
En el capítulo 6 está dedicado al cálculo de las Propiedades Dinámicas de una
estructura, como los períodos y modos de vibración pero para completar el ejercicio se
presenta en la Tabla 5.1, los períodos de vibración, frecuencia natural y modos de vibración, de
la estructura que se está analizando y en la figura 5.26 se dibujan dichos modos.
Tabla 5.1 Propiedades Dinámicas de estructura analizada con base empotrada.
Modo 1 Modo 2 Modo 3 Modo 4
Período (s.) 0.7076 0.2260 0.1230 0.0834
Frecuencia (1/s.) 8.8799 27.8023 51.0922 75.3812
Modo de
vibración
-0.0527 0.1428 0.2124 -0.1854
-0.1310 0.2048 0.0117 0.2084
-0.1947 0.0379 -0.2032 -0.1483
-0.2360 -0.2198 0.1414 0.0598
Figura 5.26 Modos de vibración con base empotrada.
En el capítulo 7 se estudia el cálculo de la matriz de amortiguamiento. Pero por el
mismo argumento de poder resolver el ejercicio, se coloca esta matriz.
[ ]
m3
m4
Modo 1 Modo 2 Modo 3 Modo 4
Modos de vibración con Base empotrada
m1
m2
m3
m4
m1
m2
m3
m4
m1
m2
m3
m4
m1
m2](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-201-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
191
EJEMPLO 6
En la figura 5.27 se presenta el modelo para el análisis sísmico de la estructura con
aisladores de base. En la planta baja se ha construido una losa maciza de 10 cm., de espesor,
sobre vigas, que se denomina losa de aislación. Este peso más el peso de las columnas de la
planta baja y el peso de los aisladores es de 1.815 T/m. Al multiplicar este peso por 19.20 y al
dividir para la aceleración de la gravedad se encuentra .
En la tabla 5.2 se presentan las propiedades dinámicas de la estructura con aisladores
de base y en la figura 5.28 se dibujan los modos de vibración. Para la estructura con aisladores
de base es importante tener presente que se trabaja con coordenadas relativas.
Se pide encontrar las matrices de masa, rigidez y amortiguamiento de la estructura con
aisladores de base de la figura 5.27. Además dibujar los modos de vibración.
Figura 5.27 Estructura de 4 pisos con aisladores
SOLUCIÓN
[ ]
[ ]
1.815 T/m
m m
m
1
mb
3,6
m
m
m
m
7,1 5 7,1
3,6
3,6
3,6
2
3
4
5
m1
m2
m3
m4
4.00 T/m
4.97 T/m
4.97 T/m
4.97 T/m](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-202-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
192
[ ]
√
√
[ ]
Tabla 5.2 Propiedades Dinámicas de estructura analizada con aislamiento sísmico.
Modo 1 Modo 2 Modo 3 Modo 4 Modo 5
Período (s.) 2.10 0.37 0.17 0.10 0.07
Frecuencia
(1/s.)
2.998 17.078 36.614 62.222 86.519
Modo de
vibración
0.143 0.217 0.226 -0.244 -0.321
0.006 -0.039 -0.149 0.297 0.521
0.014 -0.162 -0.404 0.401 0.183
0.020 -0.317 -0.356 0.034 0.394
0.023 -0.443 -0.034 0.352 0.295
Figura 5.28 Modos de vibración de la estructura con aisladores de base.
Se deja que el lector comente la forma de los modos de vibración encontrados,
especialmente del primer modo.
5.10 ANÁLISIS ESPACIAL
En la figura 5.29, se presenta el modelo en el cual, se considera que la losa es
totalmente rígida en el plano; de tal manera que en cada piso se tiene, tres grados de libertad
por planta, que son la componente de desplazamiento horizontal en sentido X; la componente
m1
m2
m3
m4
mb
m1
m2
m3
m4
mb
m1
m2
m3
m4
mb
m1
m2
m3
m4
mb
m1
m2
m3
m4
mb
Modo 1 Modo 2 Modo 3 Modo 4 Modo 5
Modos de vibración con aislamiento sísmico](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-203-320.jpg)



![SISTEMAS DE UN GRADO DE LIBERTAD
196
2
2
2
2
1
2
2
1
395
.
2
00
.
4
00
.
4
12
898
.
0
898
.
0
8
.
9
8
.
8
s
m
T
J
J
m
s
T
m
m
395
.
2
395
.
2
898
.
0
898
.
0
J
m
[ ]
La matriz de rigidez lateral de los pórticos, se la obtuvo con el programa rlaxinfi,
trabajando con inercias gruesas. Como todas las columnas son iguales (30/30 cm.) y las vigas
son iguales (25/25 cm.) la matriz de rigidez lateral de todos los pórticos son iguales.
* +
Se considera que el C.M., coincide con el centro de gravedad de la planta. Con ésta
hipótesis que es válida en estructuras en las cuales las masas están distribuidas en forma
simétrica se hallan las siguientes matrices
* + * +
* + * +
Al emplear la ecuación (5.28) se halla:
[ ]
5.10.3 Programa matriz_es
Este programa sirve para el cálculo de la matriz de rigidez en coordenadas de piso, de
estructuras que tengan el centro de masas colineal o no colineal. Antes de utilizar este
programa se debe determinar la matriz de rigidez lateral de cada uno de los pórticos, tanto en
sentido X, como en sentido Y.
[KE]=matriz_es(ntot,iejes,r,NP,KL,RT)
Los datos para el programa matriz_es son los siguientes.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-207-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
197
ntot Número total de pórticos tanto en sentido X, como en sentido Y.
iejes Número de pórticos en la dirección del análisis sísmico. Si se realiza el análisis sísmico
en sentido X, se indicará el número de pórticos en ese sentido. Lo propio para el
sentido Y.
r Este vector sirve para cuando el centro de masas es colineal. La estructura de la figura
5.30 tiene el centro de masas colineal para ese caso los datos para el análisis sísmico
en X serían [ ]. Se da un solo valor de la distancia del centro de
masa al pórtico, con este dato el programa encuentra las matrices indicadas en el
ejemplo anterior. Donde es la identificación del pórtico. Si la estructura no tiene el
centro de masa colineal igual se debe dar un valor a .
El programa pregunta si la estructura es regular o irregular. Si es regular el programa
trabaja con el vector . Si la estructura es irregular el programa ignora al vector y
trabaja con la matriz , que se indicará más adelante.
NP Es el número de pisos que tiene la estructura.
KL Matriz que contiene las matrices de rigidez lateral de cada uno de los pórticos. Primero
se debe colocar las matrices de los pórticos en el sentido de análisis y luego las
matrices de rigidez lateral de los pórticos en sentido perpendicular.
RT Es obligatorio indicar este matriz. Cuando se trata de estructuras regulares se da
. Cuando es rregular el programa ignora . Para estructuras irregulares, la
matriz está compuesta por las matrices indicadas en el ejemplo anterior, para
cada uno de los pórticos.
Para el ejemplo 7, los datos y forma de usar el programa matriz_es, es la siguiente:
El programa presenta la matriz de rigidez en coordenadas de piso indicada en el
ejemplo 7.
function [KE]=matriz_es(ntot,iejes,r,NP,KL,RT)
%
% Programa que calcula la Matriz de rigidez en coordenadas de piso
% considerando tres grados de libertad por planta, dos desplazamientos
% horizontales y una rotación de piso
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-----------------------------------------------------------------------
% [KE]=matriz_es(ntot,iejes,r,NP,KL,RT)
%-----------------------------------------------------------------------
% Datos
% iejes= # de ejes de columnas en dirección de análisis sísmico.
% ntot Número total de pórticos.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-208-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
198
% NP Número de Pisos
% KL= Matriz que contiene las matrices de rigidez lateral de todos los
% pórticos. Primero los de sentido X.
% r= Vector que contiene la distancia del pórtico al centro de masa, de
% cada uno de los pórticos, con signo, positivo anti horario.
% RT= archivo de datos que contiene todos los vectores r en el caso de que
% la estructura sea irregular Pero hay que dar esta información.
% Si el Centro de Masas es colineal RT=r.
%-------------------------------------------------------
% Reporta
% KE Matriz de rigidez en coordenadas de piso.
%--------------------------------------------------------
nx=iejes; ny=ntot-nx;
%Submatrices de rigidez: KEE
Kxx=zeros(NP,NP);Kyy=zeros(NP,NP);Kteta=zeros(NP,NP);cero=zeros(NP,NP);
Kxt=zeros(NP,NP);Kyt=zeros(NP,NP);for k=1:NP;identidad(k,k)=1;end;
te=input('n Tipo de estructura : Regular=1 Irregular=2 n ');
if te==1
for i=1:ntot
for k=1:NP
rtet(k,k)=r(i);
end
rteta=rtet*rtet;
ji=NP*(i-1)+1;jf=NP*(i-1)+NP;
if i<=nx
Kxx=Kxx+KL(ji:jf,1:NP);Kxt=Kxt+KL(ji:jf,1:NP)*rtet;
Kteta=Kteta+KL(ji:jf,1:NP)*rteta;
A(ji:ji+NP-1,:)=[identidad cero rtet];
else
Kyy=Kyy+KL(ji:jf,1:NP);Kyt=Kyt+KL(ji:jf,1:NP)*rtet;
Kteta=Kteta+KL(ji:jf,1:NP)*rteta;
A(ji:ji+NP-1,:)=[cero identidad rtet];
end
end
elseif te==2;
rtet=zeros(NP,NP);
n=1
for i=1:ntot;
rtet=RT(n:i*NP,:);
n=n+NP;
rteta=rtet*rtet;
ji=NP*(i-1)+1;jf=NP*(i-1)+NP;
if i<=nx
Kxx=Kxx+KL(ji:jf,1:NP);Kxt=Kxt+KL(ji:jf,1:NP)*rtet;
Kteta=Kteta+KL(ji:jf,1:NP)*rteta;
A(ji:ji+NP-1,:)=[identidad cero rtet];
else
Kyy=Kyy+KL(ji:jf,1:NP);Kyt=Kyt+KL(ji:jf,1:NP)*rtet;
Kteta=Kteta+KL(ji:jf,1:NP)*rteta;
A(ji:ji+NP-1,:)=[cero identidad rtet];
end
end
end
%Matriz de rigidez espacial con 3 grados de libertad por planta
KE=[Kxx cero Kxt;cero Kyy Kyt;Kxt Kyt Kteta];
return](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-209-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
199
5.11 EJERCICIO DE REFUERZO
EJEMPLO 8
En la estructura, que se encuentra a la izquierda, de la figura 5.31, las barras AB y BC
son homogéneas, de sección constante y de masas respectivamente; la barra CD es
totalmente flexible. En la parte central de la figura 5.31, se indican los dos grados de libertad
que tiene la estructura, se pide encontrar la Matriz de Masas. (Lamar, 1981)
Figura 5.31 Estructura de Ejemplo 8, grados de libertad y diagrama de velocidades.
SOLUCIÓN
A la derecha de la figura 5.31 se indica el diagrama de distribución de velocidades, se
deja al lector la comprobación respectiva.
̇ 0 ̇ ( ̇ ) 1 ̇
Luego de reemplazar y factorar se halla la matriz de masas.
[ ]
EJEMPLO 9
En la figura 5.32 se presenta el modelo numérico de análisis sísmico de una estructura
de acero de lámina delgada, la misma que va a ser analizada con un modelo de piso flexible.
Las masas discretas valen en los extremos y en el cumbrero. Se pide encontrar la matriz
de masas, considerando que cada masa tiene tres desplazamientos: dos horizontales y un
vertical.
SOLUCIÓN
En la figura 5.33 se presentan los grados de libertad de la estructura, en total se tienen
18 grados de libertad. En cada nudo existe una componente de desplazamiento horizontal en
dirección X, otra en dirección Y, y otra en dirección vertical.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-210-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
201
De donde:
[ ]
Donde es la matriz de masas para cuando solo se considera sismo en dirección
transversal; es la matriz de masas para cuando solo se considera la acción sísmica en
sentido longitudinal; es la matriz de masas para cuando el sismo actúa en sentido vertical.
Estas matrices valen.
[ ] [ ]
La matriz de rigidez tiene una forma similar y vale.
[ ]
Donde , , , son las matrices de rigidez asociadas a las coordenadas:
transversales, longitudinales y verticales, respectivamente. Estas matrices se obtienen con los
vectores de colocación los mismos que están compuestos por los grados de libertad indicados
en la figura 5.33. Así por ejemplo, para hallar los vectores de colocación para el pórtico
transversal primero son [ ] y para el segundo pórtico transversal son [ ]; de
tal manera que se encuentran las matrices de rigidez de los pórticos transversales en
coordenadas principales y se ubican en la diagonal de ; es un modelo aproximado ya que
no se considera el acoplamiento de los pórticos longitudinales (igual sucede cuando se analiza
con un modelo de Piso Rígido).
COMENTARIO
Las estructuras de acero para cubrir piscinas, laboratorios, auditorios, se construyen
con modelos similares al indicado en la figura 5.32, se tienen dos ejes de columnas en el
sentido longitudinal y varios ejes de columnas en el sentido transversal.
La luz en el sentido transversal, por lo general está alrededor de los 20 m., como es
importante esta luz que se cubre con dos columnas, la viga tiene dimensiones considerables,
de tal manera que la estructura es bastante rígida en sentido transversal.
En el sentido longitudinal los pórticos se encuentran cada 4 o 5 m. AL pensar solo en
cargas verticales, no es necesario colocar vigas en sentido longitudinal sino únicamente
correas formadas por un perfil G y en el cumbrero se acostumbra colocar una doble G. Ahora
bien al considerar el sismo, estas estructuras son sumamente vulnerables en sentido
longitudinal ya que son muy flexibles. Aguiar (2012).
Por lo tanto, se recomienda que en estructuras de acero de lámina delgada se piense
en el sismo y se le confiera mayor rigidez en sentido longitudinal. Por ejemplo para la
estructura de la figura 5.32 hace falta una columna en la mitad del pórtico (bajo el cumbrero).
En Aguiar (2012) se presenta el reforzamiento sísmico realizado en 3 piscinas de Quito; en una
vivienda de interés social y en un laboratorio.
(5.32)
(5.33)
(5.34)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-212-320.jpg)








![SISTEMAS DE UN GRADO DE LIBERTAD
210
o
M
2
1
Al reemplazar (6.13) en (6.12) se tiene:
o
o M
M
M
K
2
1
2
1
Por otro lado se tiene que:
2
1
2
1
M
M
M
Al reemplazar en la última ecuación se encuentra:
o
o M
M
K
2
1
2
1
Al multiplicar por la izquierda, por 2
1
M se obtiene:
o
o
M
K
M
2
1
2
1
Se denomina
2
1
2
1
M
K
M
Ko
De donde, la ecuación ( 6.14 ) se transforma en:
o
o
o
K
El procedimiento de cálculo para encontrar los valores y vectores propios de una
estructura aplicando el algoritmo de 2
1
M es el siguiente:
1. Se encuentra la matriz 2
1
M . Normalmente la matriz de masas es diagonal de
tal manera que 2
1
M se encuentra sacando la raíz cuadrada de los elementos
de la diagonal.
2. Se determina 2
1
M . Para el caso de matrices diagonales no es más que la
inversa de los elementos de la diagonal.
3. Se determina o
K .
4. Se aplica cualquier Método de cálculo de valores y vectores propios en o
K .
5. Finalmente se hallan los vectores propios o
M
2
1
El programa modosplano escrito en MATLAB determina los períodos y modos de
vibración de pórticos planos, utilizando el algoritmo de 2
1
M . Previamente el usuario habrá
obtenido con otro programa la matriz de rigidez lateral o carga esta matriz. La forma de uso, es:
[Modos]=modosplano (K)
K es la matriz de rigidez lateral del pórtico.
Modos son los modos de vibración del pórtico.
(6.13)
(6.14)
(6.15)
(6.16)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-221-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
211
function [Modos]=modosplano(K)
%
% Calculo de modos de vibracion de porticos planos.
% Empleando algoritmo de M elevado a la 1/2.
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
% -----------------------------------------------------------------
% [Modos]=modosplano(K)
% -----------------------------------------------------------------
% K Matriz de rigidez lateral del portico plano
% M Matriz de masas, se programa como vector ya que es diagonal
% NP Numero de pisos.
% Por pantalla se indicara las masas de cada piso.
% Previamente el usuario habra calculado la matriz de rigidez lateral
% con otro programa.
% T Periodos de vibracion.
%
NP = input (' n Numero de pisos ');
for i=1:NP
fprintf ('Indique la masa del piso , %2d',i);
M(i) = input (', Valor de la masa: ');
end
M12=sqrt(M);
for i=1:NP
M12(i)=1.0/M12(i);
end
MINV=zeros(NP,NP); MINV=diag(M12); Ko=MINV*K*MINV;
[V,D]=eig(Ko); Modos=MINV*V; Wn=sqrt(D); T=diag(Wn);
for i=1:NP
T(i)=2*pi/T(i);
end
fprintf ('n Periodos de vibracion ')
T
fprintf ('n Modos de vibracion ')
Modos;
% ---fin
EJEMPLO 4
Encontrar los períodos y modos de vibración de la estructura de la figura 6.2. Si
2
/
21
.
1738965 m
T
E . La carga es uniforme distribuida en cada piso y tiene una magnitud
de 2.0 T/m., aplicando el algoritmo de 2
1
M .
SOLUCIÓN
Al multiplicar la carga uniforme repartida por la longitud total de 8 m., y al dividir por el
valor de la gravedad, se encuentra la masa concentrada en cada piso, que vale 1.633 Ts
2
/m.
La matriz de rigidez y la matriz de masas para el cálculo del problema de valores y
vectores propios, son:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-222-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
213
Figura 6.3 Modos de vibración
El cálculo de los valores y vectores propios, en la matriz o
K se hallaron aplicando el
Método de Jacobi que se indica en el siguiente apartado.
Si se desea encontrar los períodos de vibración con el programa modosplano se debe
proceder de la siguiente manera:
>> K=[2761.1 -1538.1 285.7; -1538.1 2278.0 -1080.6; 285.7 -1080.6 836.9]
>> [Modos] = modos plano(K)
Numero de pisos 3
Indique la masa del piso, 1, Valor de la masa: 1.633
Indique la masa del piso, 2, Valor de la masa: 1.633
Indique la masa del piso, 3, Valor de la masa: 1.633
Luego el programa reporta los períodos y modos indicados en el ejemplo. Con la
salvedad que está cambiado de signo los valores del tercer modo pero esto no tiene
trascendencia ya que los modos son una base.
MATLAB presenta otra opción para calcular directamente los valores y vectores
propios directamente, por consola, utilizando el comando eig pero de forma diferente a la que
está en el programa modosplano. Pero el programa eig de MATLAB no presenta los valores
propios ordenados de menor a mayor, eso lo hace el programa orden_eig de CEINCI-LAB que
se verá posteriormente.
EJEMPLO 5
Determinar, por consola, los valores y vectores propios del ejemplo 4.
SOLUCIÓN
>> K=[2761.1 -1538.1 285.7; -1538.1 2278.0 -1080.6; 285.7 -1080.6 836.9];
>> M=[1.633 0 0; 0 1.633 0; 0 0 1.633];
>> [V,D] = eig (K,M)
En V se encuentran los modos de vibración o vectores propios y en D los valores
propios.
PRIMER MODO SEGUNDO MODO
47
TERCER MODO](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-224-320.jpg)








![SISTEMAS DE UN GRADO DE LIBERTAD
222
1 4 7 1 10 13; 1 10 13 1 16 19; 2 5 8 2 11 14; 2 11 14 2 17 20];
LH=[2.9; 2.9; 2.9; 2.9; 2.9; 5.7; 1.9; 5.7; 1.9];
senoH=[1; 1; 1; 1; 1; 0; 0; 0; 0];
cosenoH=[0; 0; 0; 0; 0; 1; 1; 1; 1];
ELEMH=[0.3 0.8;0.3 0.8; 0.001 0.001; 0.3 0.8;0.3 0.8;0.3 0.7;0.3 0.3;
0.3 0.7; 0.3 0.3];
EH=1800000; % Modulo de elasticidad del Hormigón
[SH]=krigidez(ngl,ELEMH,LH,senoH,cosenoH,VCH,EH);% K elemen. Hormigón
%--------------Acero---------------------------------------
VCA=[1 16 19 2 17 20; 2 5 8 3 6 9;2 11 14 3 12 15;2 17 20 3 18 21;3 6
9 3 12 15;3 12 15 3 18 21];
LA=[2.9; 2.9; 2.9; 2.9; 5.70; 1.9];
senoA=[1; 1; 1; 1; 0; 0]; cosenoA=[0; 0; 0; 0; 1; 1];A=0.001801;
Ix=0.0000097468;
ELEMA=[A Ix; A Ix; A Ix; A Ix; A Ix; A Ix];
EA=21000000; % Modulo de elasticidad del Acero
[SA]=krigidez_acero(ngl,ELEMA,LA,senoA,cosenoA,VCA,EA); % K Acero
%------------------------------------------------------------
S=SH+SA; % Matriz de rigidez Acero y Hormigón
Kaa=S(1:3,1:3); Kab=S(1:3,4:21); Kbb=S(4:21,4:21);Kba=Kab';
K=Kaa-Kab*inv(Kbb)*Kba % Matriz de rigidez en coordenadas principales
%end
La matriz de rigidez lateral que se obtiene es:
[ ]
Tabla 6.1 Cálculo de las masas en estructura con base empotrada.
Piso D
L D+0.25L
Ancho
cooperante Carga q Longitud
Carga
P
Masa
m
No T/m² T/m² T/m² M T/m m T Ts2
/m
1 0.76 0.25 0.82 4.5 3.70 7.60 28.13 2.870
2 0.65 0.25 0.71 4.5 3.21 7.60 24.37 2.486
3 0.05 0 0.05 4.5 0.23 7.60 1.71 0.174
[ ]
En la tabla 6.2 se presentan las propiedades dinámicas que se hallan en la estructura
con base empotrada utilizando el programa orden_eig de la librería de CEINCI-LAB
Tabla 6.2 Propiedades dinámicas en estructura con base empotrada.
Modo 1 2 3
Período (seg.) 0.2345 0.1670 0.0569
0.1699 0.1914 -0.5319
0.4121 0.3965 0.2743
1.6865 -1.7021 -0.0737
Los valores del Primer Modo de vibración están indicando que el tercer piso es muy
flexible ya que se va a desplazar aproximadamente cuatro veces de lo que se desplaza el
segundo piso; algo similar se tiene para el segundo modo. Las estructuras responden
fundamentalmente en el primer modo.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-233-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
224
( ) ( )
( ) ( )
[ ]
La masa de los dos plintos, vale:
En la figura 6.8 se presenta el modelo considerado para la interacción suelo estructura,
se indican los grados de libertad y las alturas a cada una de las masas medidas a partir de la
cimentación, para la evaluación de la matriz de masas.
Figura 6.8 Modelo considerado para la interacción suelo estructura.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-235-320.jpg)


![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
227
. /
El aislador de la figura 6.10 es esquemático; la goma tiene 4 mm., de espesor y las
placas de acero 2 mm. Si se dibuja todas las gomas, la figura va a ser muy grande.
Figura 6.10 Dimensiones del aislador elastomérico a utilizar.
EJEMPLO 8
Encontrar la matriz de rigidez de la estructura indicada en la figura 6.9, la matriz de
masas y los períodos de vibración, utilizando los programas de CEINCI-LAB. Modelar a los
aisladores como resortes que tienen una rigidez , considerar los grados de
libertad indicados en la figura 6.11, la losa de aislación solo tiene un grado de libertad en el
piso, que se ha definido con la coordenada 1 y considerar los desplazamientos laterales de la
superestructura con relación al desplazamiento lateral del sistema de aislación.
Las dimensiones de las columnas son de 45/60 y las vigas de los tres primeros pisos
son de 35/60 y del cuarto piso de 35/50. El módulo de elasticidad del hormigón es 2168870
T/m
2
. En el modelo numérico de la figura 6.11, no influye las dimensiones de la viga de la losa
de aislación.
SOLUCIÓN
En el capítulo 5 se resolvió este problema, considerando que todos los elementos de la
superestructura son axialmente rígidos, para el efecto se utilizó el programa rlaxinfi. Ahora de
acuerdo al modelo de la figura 6.11, solo las vigas son axialmente rígidas, de tal manera que la
matriz de rigidez lateral es diferente. Pero los períodos de vibración y formas modales son los
mismos o difieren muy poco, razón por la cual se presenta el programa con el cual se resuelve
el ejercicio y los programas de CEINCI-LAB que se han utilizado, en el siguiente apartado. Las
matrices de rigidez y masa, son:
[ ]](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-238-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
228
[ ]
Figura 6.11 Grados de libertad y coordenadas principales.
Tabla 6.4 Propiedades Dinámicas de estructura con aisladores de base
Modo 1 2 3 4 5
Período (seg.) 2.10 0.38 0.18 0.10 0.08
-0.1419 -0.2168 0.2262 0.2431 -0.3217
-0.0063 0.0388 -0.1483 -0.2956 0.5222
-0.0147 0.1613 -0.4039 -0.4002 0.1846
-0.0208 0.3156 -0.3559 -0.0327 0.3947
-0.0245 0.4423 -0.0347 -0.3510 0.2962
El programa que se indica a continuación, encuentra las matrices de rigidez, masa,
periodos de vibración, modos de vibración, que se han anotado y también halla la matriz de
amortiguamiento, tema que se estudia en el siguiente capítulo y encuentra la respuesta en el
tiempo ante la componente horizontal del sismo de El Centro de 1940 utilizando el algoritmo de
Procedimiento de Espacio de Estado que se estudiará posteriormente; se presenta todo en
este ejemplo para tener completa la respuesta.
% Ejemplo 8
%
% Dr. Roberto Aguiar
% 18 Nov 2011
%-----------------------------------------------------------
nod=20;np=4;nr=4;
[CG,ngl]=cg_aislador(nod,np,nr);
GEN=[1 1 5 3 1 1 1;5 5 9 3 1 1 1;9 9 13 3 1 1 1; 13 13 17 3 1 1 1;
17 1 2 2 1 1 1; 20 5 6 2 1 1 1; 23 9 10 2 1 1 1; 26 13 14 2 1 1 1;
29 17 18 2 1 1 1];
[NI,NJ]=gn_portico(GEN);
30
31
32
33
34
35
36
37
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
m1
m2
m3
m4
1
mb
6
7
8
9
10
11
2
3
4
5
1](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-239-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
229
[VC]=vc_aislador(NI,NJ,CG);
NUDOS=[1 0.0 0.0 4 4 0.0 3.6; 2 7.1 0.0 4 4 0.0 3.6;
3 12.1 0.0 4 4 0.0 3.6; 4 19.2 0.0 4 4 0.0 3.6];
[X,Y]=glinea_portico(NUDOS);
% dibujo(X,Y,NI,NJ);
[L,seno,coseno]=longitud (X,Y,NI,NJ);
ELEM=[0.45 0.60;0.45 0.60;0.45 0.60;0.45 0.60;
0.45 0.60;0.45 0.60;0.45 0.60;0.45 0.60;
0.45 0.60;0.45 0.60;0.45 0.60;0.45 0.60;
0.45 0.60;0.45 0.60;0.45 0.60;0.45 0.60;
0.35 0.60; 0.35 0.60; 0.35 0.60;
0.35 0.60; 0.35 0.60; 0.35 0.60;
0.35 0.60; 0.35 0.60; 0.35 0.60;
0.35 0.60; 0.35 0.60; 0.35 0.60;
0.35 0.50; 0.35 0.50; 0.35 0.50];
E=2168870;
kb=[100.3; 100.3; 100.3; 100.3];
[SS]=krigidez_aislador(ngl,ELEM,L,seno,coseno,VC,E,kb);
Kaa=SS(1:5,1:5);Kab=SS(1:5,6:37);Kbb=SS(6:37,6:37);Kba=Kab';
K=Kaa-Kab*inv(Kbb)*Kba% Matriz de rigidez de aislación estructura
masas=[3.56;9.74;9.74;9.74;7.84];
[M]=masas_aislador (masas) % Matriz de masas de aislación estructura
[T,fi,OM]=orden_eig(K,M) % Estructura con aislación
zedas=0.05;% Superestructura
Ks=K(2:5,2:5);Ms=M(2:5,2:5);
[Ts,fis,OMs]=orden_eig(Ks,Ms); % Estructura con base empotrada
[Cs]=amortiguamiento(Ms,fis,OMs,zedas) % Amortiguamiento Base Empotrada
mt=M(1,1); % Masa total
zedab=0.10; % Amortiguamiento Aislador
cb=2*zedab*sqrt(mt*sum(kb));
cero=[0 0 0 0];
C=[cb cero;cero' Cs]; % Matriz de amortiguamiento con Aisladores
J=[1;0;0;0;0]; % Vector de Incidencia
load rec_centro; %Sismo de El Centro de 1940
p=ux/100; % Paso el acelerograma a m/s2.
n=length (p); % Numero de puntos del sismo
for i=1:5; q(i)=0; qp(i)=0; end; q=q'; qp=qp'; Y=[q;qp]
for i=1:n
a=p(i); % Un valor del acelerograma
t(i)=i*dT; % Tiempo
[Yn]=pee_de_uno(K,C,M,J,a,dT,Y);
qb(i)=Yn(1); % Desplazamiento del sistema de aislación
qt(i)=Yn(5); % Desplazamiento en el tope de la estructura
qt1(i)=Yn(2); %Desplazamiento en el primer piso
Y=Yn;
end
figure (1) % Acelerograma
plot(t,p);xlabel ('Tiempo'); ylabel ('Aceleracion'); title ('Acelerograma');
figure (2) % Desplazamiento Sistema de Aislación
plot(t,qb);xlabel ('Tiempo'); ylabel ('Desplazamiento'); title ('Aislacion');
figure (3); % Desplazamiento de Superestructura cuarto piso
plot (t,qt); hold on; plot (t,qt1,'r');
xlabel ('Tiempo'); ylabel ('Desplazamiento'); title ('1er Piso 4to piso');
figure (4)
plot(t,qb); hold on; plot (t,qt,'r');
xlabel ('Tiempo'); ylabel ('Desplazamiento'); title ('Aislacion-Super estructura');](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-240-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
230
6.7 PROGRAMAS DE CEINCI-LAB PARA AISLADORES DE BASE
Para que se entienda el archivo de datos del ejemplo 8, que se acaba de presentar y
sobre todo para comprender los programas de la librería de CEINCI-LAB, se presenta en la
figura 6.12, la numeración de los nudos dentro de un rectángulo, de los elementos dentro de un
círculo, se ha numerado las coordenadas principales de primero, del 1 al 5, luego los restantes
grados de libertad y a la derecha se indica el modelo de cálculo para el análisis sísmico.
Figura 6.12 Numeración de nudos, elementos y grados de libertad.
Programa cg_aislador
[CG,ngl]=cg_aislador (nod,np,nr)
Este programa calcula, la matriz que contiene a las Coordenadas Generalizadas de
cada uno de los nudos y el número de grados de libertad de la estructura. Para los nudos del
sistema de aislación 1, 2, 3 y 4; este arreglo es [ 1 0 0 ], solo puede desplazarse en sentido
horizontal. Es decir este programa reproduce los grados de libertad que están indicados en la
figura 6.12. Los datos de entrada, son:
nod Número de nudos del pórtico.
np Número de pisos.
nr Número de nudos restinguidos.
function [CG,ngl]=cg_aislador(nod,np,nr)
%
% Programa para encontrar las coordenadas generalizadas
% en un Portico Plano con Aisladores de Base sobre la cimentación
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [CG,ngl]=cg_aislador(nod,np,nr)
%-------------------------------------------------------------
% CG Matriz de coordenadas generalizadas
% nod Numero de nudos
2
3
4
5
m1
m2
m3
m4
1
mb
2
3
4
5
1
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
1 2
6
9
13
17 18
14
10
5
3
7
11
15
19
4
8
12
16
20
5
17 18 19
22
21
20
23 24 25
28
27
26
29 30 31
6 7 8
4
3
2
1
12
11
10
9
16
13 14 15](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-241-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
231
% np Numero de pisos
% nr Numero de nudos con aisladores de base sobre cimentacion
%
ngl=0;CG=zeros(nod,3);
for i=1:nr
CG(i,1)=1;
end
ngl=ngl+1;icon=nr;
%------------Coordenadas Principales----------------------------
for i=1:np
ngl=ngl+1;
for j=1:nr
nn=icon+j;
CG(nn,1)=ngl;
end
icon=nn;
end
%-----------Coordenadas Secundarias----------------------------
icon=nr;
for i=1:np
for j=1:nr
nn=icon+j;ngl=ngl+1;
CG(nn,2)=ngl;
ngl=ngl+1;
CG(nn,3)=ngl;
end
icon=nn;
end
return
Programa gn_portico
[NI,NJ]=gn_portico (GEN)
Este programa obtiene dos vectores denominados NI, NJ que contienen los nudos
iniciales y finales del pórtico. Los datos de ingreso vienen en la matriz GEN, el usuario podrá
ver el significado de cada variable de ingreso en el programa que se indica a continuación.
function [NI,NJ]=gn_portico(GEN)
%
% Programa para generar el Nudo inicial y final de los elementos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Septiembre de 2009
% Revisado Septiembre 2011
%-------------------------------------------------------------
% [NI,NJ]=gn_portico(GEN)
%-------------------------------------------------------------
% GEN=[i,ia,ib,nig,ii,ina,inb]
% i Número del elemento
% ia Nudo inicial del elemento
% ib Nudo final del elemento
% nig Número de elementos a generar
% ii Incremento en la numeración de los elementos
% ina Incremento en la numeración del nudo inicial
% inb Incremento en la numeración del nudo final](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-242-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
232
% NI,NJ Vectores con los nudos iniciales y finales generados
nf=length(GEN(:,1));
for ij=1:nf
i=GEN(ij,1);ia=GEN(ij,2);ib=GEN(ij,3);nig=GEN(ij,4);
ii=GEN(ij,5);ina=GEN(ij,6);inb=GEN(ij,7);
NI(i)=ia;NJ(i)=ib;
for k=1:nig
i=i+ii;NI(i)=ia+ina;NJ(i)=ib+inb;
ia=NI(i);ib=NJ(i);
end
end
return
% ---end---
Programa vc_aislador
[VC]=vc_aislador (NI,NJ,CG)
Este programa halla la matriz que contiene a los vectores de colocación de cada uno
de los elementos de la estructura. Este programa es diferente al vc_portico debido a que
ahora se trabaja con coordenadas relativas. Si se trabajará con el programa vc_portico, el
vector de colocación del elemento 1, sería: [1 0 0 2 6 7]. Pero como los desplazamientos de la
superestructura son relativos al sistema de aislación, el vector de colocación es [0 0 0 2 6 7] y
esto se obtiene con el programa vc_aislador
Los datos de entrada son: NI, NJ , vectores que contienen al nudo inicial y final de la
estructura y CG que es la matriz que contiene a las coordenadas generalizadas.
function [VC]=vc_aislador(NI,NJ,CG)
%
% Programa para calcular la matriz con los vectores de colocación
% en Porticos Planos con Aisladores de Base.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [VC]=vc(NI,NJ,CG)
%-------------------------------------------------------------
% NI Vector con los nudos iniciales de los elementos
% NJ Vector con los nudos finales de los elementos
% CG Matriz que contiene las coord. generalizadas de nudos
mbr=length(NI);icod=length(CG(1,:));VC=zeros(mbr,icod);
for i=1:mbr
for j=1:icod
VC(i,j)=CG(NI(i),j);VC(i,j+icod)=CG(NJ(i),j);
end
if VC(i,1)==1
if VC(i,4)==1
continue
else
VC(i,1)=0;
end
end
end
return
% ---end----](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-243-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
233
Programa glinea_portico
[X,Y]=glinea_portico (NUDOS)
Este programa obtiene dos vectores denominados X, Y, con las coordenadas en
sentido X, Y, de cada uno de los nudos de la estructura. El ingreso de datos se realiza en la
matriz NUDOS, el contenido de esta matriz se ve en el listado del programa que se indica a
continuación.
function [X,Y]=glinea_portico(NUDOS)
%
% Programa para generar las coordenadas de los nudos en forma lineal
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Septiembre de 2009
%-------------------------------------------------------------
% [X,Y]=glinea_portico(NUDOS)
%-------------------------------------------------------------
% NUDOS=[i,xi,yi,ij,inci,dx,dy]
% i Nudo inicial
% xi,yi Coordenadas del nudo inicial
% ij Numero de nudos a generar
% inci Incremento en la numeración del nudo inicial
% dx Incremento de longitud en X.
% dy Incremento de longitud en Y.
% X,Y Vector que contiene las coordenadas de los nudos
nf=length(NUDOS(:,7));
for k=1:nf
i=NUDOS(k,1);X(i)=NUDOS(k,2);Y(i)=NUDOS(k,3);
ij=NUDOS(k,4);inci=NUDOS(k,5);
dx=NUDOS(k,6);dy=NUDOS(k,7);
for ii=1:ij
X(i+ii*inci)=X(i)+ii*dx;
Y(i+ii*inci)=Y(i)+ii*dy;
end
end
return
Programa longitud
[L,seno,coseno]=longitud (X,Y,NI,NJ)
Este programa halla tres vectores que se han denominado L, seno, coseno, que contiene
la longitud de cada uno de los elementos, el primer vector; el seno del ángulo que forma el eje
del miembro con el eje de las X, y el coseno del ángulo anterior. Esta información sirve para
obtener la matriz de rigidez en coordenadas globales. En la figura 6.13 se indica, a la izquierda
un elemento inclinado que forma un ángulo , con la horizontal; la longitud del elementos se
halla con las coordenadas X, Y, del nudo inicial y final, por eso son datos los vectores X, Y, que
contienen las coordenadas de todos los nudos; NI, NJ, los vectores con la información del nudo
inicial y final de cada elemento.
Con los valores del seno y coseno se halla la matriz de paso de coordenadas locales a
globales. Aguiar (2004).](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-244-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
234
Figura 6.13 Coordenadas Locales y Globales de un elemento.
function [L,seno,coseno]=longitud (X,Y,NI,NJ)
%
% Programa que calcula longitud, seno, coseno de los elementos
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Septiembre de 2009
%-------------------------------------------------------------
% [L,seno,coseno]=longitud (X,Y,NI,NJ)
%-------------------------------------------------------------
% X,Y Vector de coordenadas de los nudos
% NI,NJ Vector de nudos inicial y final de elementos
mbr=length(NI);
for i=1:mbr
dx=X(NJ(i))-X(NI(i));dy=Y(NJ(i))-Y(NI(i));
L(i)=sqrt(dx*dx+dy*dy);
seno(i)=dy/L(i);coseno(i)=dx/L(i);
end; return
Programa krigidez_aislador
[SS]=krigidez_aislador (ngl,ELEM,L,seno,coseno,VC,E,kb)
El programa krigidez_aislador determina la matriz de rigidez de la estructura, es similar al
programa krigidez, que obtiene la matriz de rigidez de un pórtico plano con base empotrada.
Ahora se debe dar un dato más que es:
Kb Vector que contiene la rigidez de cada uno de los aisladores.
function [SS]=krigidez_aislador(ngl,ELEM,L,seno,coseno,VC,E,kb)
%
% Programa para encontrar la matriz de rigidez de un portico plano
% o armadura plana con aisladores de base
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [SS]=krigidez_aislador(ngl,ELEM,L,seno,coseno,VC,E,kb)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-245-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
235
%-------------------------------------------------------------
% ELEM Matriz que contiene la base y la altura de los elementos
% para el caso de pórticos planos.
% ELEM Vector que contiene el área de los elementos de armadura
% L Vector que contiene la longitud de los elementos
% seno Vectorque contiene los senos de los elementos
% coseno Vector que contiene los cosenos de los elementos
% VC Matriz que contiene los vectores de colocación de elementos
% E Modulo de elasticidad del material
% SS Matriz de rigidez de la estructura
% ngl Número de grados de libertad
% kb Vector que contiene la rigidez de cada uno de los aisladores
%
mbr=length(L); SS=zeros(ngl);icod=length(VC(1,:));
for i=1:mbr
if icod==4
A=ELEM(i,1); %Area de elemento
Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kdiagonal(A,Lon,E,sen,cose);
else
b=ELEM(i,1);h=ELEM(i,2);Lon=L(i);sen=seno(i);cose=coseno(i);
[k]=kmiembro(b,h,Lon,E,sen,cose);
end
for j=1:icod
jj=VC(i,j);
if jj==0
continue
end
for m=1:icod
mm=VC(i,m);
if mm==0
continue
end
SS(jj,mm)=SS(jj,mm)+k(j,m);
end
end
end
% Contribucion de aisladores
icont=length(kb); % Numero de aisladores
for i=1:icont
SS(1,1)=SS(1,1)+kb(i);
end; return
Programa masas_aislador
[M]=masas_aislador(masas)
Programa para encontrar la matriz de masas de un pórtico plano con aisladores de
base, cuyo modelo numérico de cálculo, es similar al que está a la derecha de la figura 6.12.
Los datos se ingresan en el vector:
masas Contiene la masa del sistema de aislación , pero la total; del primer
piso , total; del segundo piso , etc. Con esta información el
programa encuentra la masa total de la estructura con sistema de
aislación que se había denominado , que es el primer elemento de la
matriz de masas.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-246-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
236
function [M]=masas_aislador(masas)
%
% Programa para encontrar la matriz de masas de una estructura
% Plana con aisladores de base elastomericos sobre la cimentacion
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2011
%-------------------------------------------------------------
% [M]=masas_aislador(masas)
%-------------------------------------------------------------
% masas Vector que contiene las masas de cada piso empezando
% por la masa de la losa de aislación; luego del primer
% piso hasta la del último piso.
ngl=length(masas); M=zeros(ngl);
for i=1:ngl
if i==1
M(i,i)=sum(masas);
else
M(i,i)=masas(i);M(1,i)=masas(i);M(i,1)=masas(i);
end
end
return
Programa orden_eig
[T,fi,OM]=orden_eig (KE,MASA)
Programa que encuentra los valores y vectores propios de una estructura, a partir de los
siguientes datos:
KE Matriz de rigidez de la estructura.
MASA Matriz de masas de la estructura.
El programa reporta:
T Períodos de vibración de la estructura de mayor a menor.
fi Modos de vibración de la estructura.
OM Frecuencias de vibración.
function [T,fi,OM]=orden_eig(KE,MASA)
%
% Programa que calcular y ordenar los valores y vectores propios
% de menor a mayor
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Octubre de 2009
%-------------------------------------------------------------
% [T,phi,OM]=orden_eig(K,M)
%-------------------------------------------------------------
% KE,MASA Matrices de rigidez y de masas
% V,OM Vectores propios y frecuencias de vibración
% T Períodos de vibración
n=length(KE);
[V,lamda]=eig(full(KE),full(MASA));
OM=sqrt(diag(lamda));[OM,ind]=sort(OM);fi=V(:,ind);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-247-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
237
for i=1:n; T(i)=2*pi/OM(i); end; T=T';
Md=diag(fi'*MASA*fi);S=sqrt(1./Md);% Normalización de modos
fi=fi*diag(S);% Normalizado de tal manera que fi'*M*fi=1
return
Programa amortiguamiento
[C]=amortiguamiento (M,phi,OM,zeda)
Programa que determina la matriz de amortiguamiento, tema que se estudiará en el
siguiente capítulo. Los datos de entrada, son:
M Matriz de masas.
phi Matriz que contiene los modos de vibración.
OM Vector con las frecuencias de vibración.
zeda Factor de amortiguamiento, un solo valor el mismo que se considera igual en
todos los modos de vibración.
function [C]=amortiguamiento(M,phi,OM,zeda)
%
% Programa para encontrar la matriz de amortiguamiento de una estructura
% Amortiguamiento tipo Wilson y Penzien
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2009
%-------------------------------------------------------------
% [C]=amortiguamiento(M,phi,OM,zeda)
%-------------------------------------------------------------
% M Matriz de masa de la estructura
% phi Matriz que contiene los modos de vibración normalizados
% OM Vector que contiene las frecuencias de vibración de menor a mayor.
% ngl Número de grados de libertad
% zeda Factor de amortiguamiento de la estructura, un solo valor
n=length(M(:,1));
ZEDA=zeros(n);for i=1:n; ZEDA(i,i)=zeda; end
mms=diag(phi'*M*phi); % mms es un vector unitario
Cd=zeros(n);for i=1:n; Cd(i,i)=2*ZEDA(i,i)*OM(i)/mms(i); end
C=M*phi*Cd*phi'*M;
return;end
Programa pee_de_uno
[Yn]=pee_de_uno (K,C,M,J,a,dT,Y)
Este programa encuentra la respuesta en el tiempo de una estructura, empleando el
Método denominado: Procedimiento de Espacio de Estado, que se estudiará más adelante.
Antes de describir los datos de entrada, es importante indicar el sistema de ecuaciones
diferenciales que se resuelve.
̈ ̇
Donde son las matrices de masa, amortiguamiento y rigidez del sistema; es el
vector de incidencia de los grados de libertad con el movimiento del suelo; es la
aceleración del suelo definida por su acelerograma; ̇ ̈ , son los vectores de desplazamiento,
velocidad y aceleración.
(6.35)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-248-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
238
En la formulación del Método: Procedimiento de Espacio de Estado, de la ecuación
(6.35) se despeja el vector ̈ .
̈ ̇
En la ecuación (6.36), están prácticamente indicados todos los datos que ingresan al
programa, faltando indicar que el vector de estado está formado por el vector de
desplazamientos y por el vector de velocidades.
* ̇ +
Los datos de entrada son:
K Matriz de rigidez.
C Matriz de amortiguamiento.
M Matriz de masas.
J Vector de incidencia de movimiento del suelo, teniendo en cuenta la forma de
escritura de la ecuación (6.36).
a Un valor del acelerograma,
dT Incremento de tiempo con el cual viene el archivo del acelerograma.
Y Vector de estado que contiene los desplazamientos y velocidades, en el tiempo
discreto .
El programa reporta, el vector de estado en el tiempo que se ha denominado .
function [Yn]=pee_de_uno(K,C,M,J,a,dT,Y)
%
% Procedimiento de Espacio de Estado pero obtiene la respuesta
% en el tiempo. En este programa se halla para cada aceleración
% del suelo la respuesta en el tiempo.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Octubre de 2009
%-------------------------------------------------------------
% [Yn]=pee_de_uno(K,C,M,J,a,dT,Y)
%-------------------------------------------------------------
% K,C,M Matrices de rigidez, amortiguamiento y masas
% J El vector de cargas Q=-M*J*a
% a Valor de una aceleración del acelerograma
% dT Incremento de tiempo
% Y Vector que contiene a los desplazamientos y velocidades
% en el tiempo discreto k. Solo se halla la respuesta para
% un solo valor de aceleración
% Yn Nuevo vector Y para tiempo discreto k+1
n=length(K);for i=1:n; cero(i)=0; end; cero=cero';
F=[zeros(n) eye(n); -inv(M)*K -inv(M)*C];
B=[cero;J];A=expm(F*dT);Bd=F(A-eye(2*n))*B;
Yn=A*Y+Bd*a;
return
Con relación a la estructura de 4 pisos, con aisladores de base, ejemplo 8; el programa
descrito en el apartado anterior y que utiliza los programas del sistema CEINCI-LAB, que se
han indicado, reporta los siguientes gráficos.
(6.36)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-249-320.jpg)








![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
247
A más de calcular el área sombreada es importante fijarse en la figura 4 y justificarse
por que se multiplica por 4 para hallar la energía disipada pero esto además ayuda a
entender el modelo bilineal. Jennings (1968)
( )
( ) ( )
Al reemplazar las áreas elementales en y luego de simplificar términos se obtiene:
( )
Para hallar la energía que absorbe el sistema se trabaja con el modelo de la rigidez
secante, que es muy utilizado en Ingeniería Sísmica, de tal manera que se debe calcular el
área sombreada de la figura 7.5.
Figura 7.5 Energía absorbida por el sistema de rigidez secante.
Una vez que se tienen calculadas las energías , para encontrar se debe
utilizar la ecuación (7.6) pero se desea obtener una ecuación en función de la demanda de
ductilidad de la estructura , definida por:
La fuerza máxima en un ciclo de carga se halla con la siguiente ecuación.
( )
Pero . Por otra parte . Luego
( )
[ ]
(7.9)
(7.10)
(7.11)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-258-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
248
Luego la energía se obtiene con la siguiente expresión:
[ ]
Ahora al desarrollar la ecuación (7.9) se tiene:
( )
Sacando factor común , y luego de factorar se halla.
Finalmente el factor de amortiguamiento equivalente se encuentra con la siguiente
ecuación. Jennings (1968)
[ ]
7.1.4 Recomendaciones del ATC-40
El amortiguamiento viscoso efectivo, para el rango no lineal eq
se puede considerar
igual al amortiguamiento viscosos inherente a la estructura , más el amortiguamiento viscoso
equivalente eq
, el mismo que se ha obtenido en el apartado anterior mediante la rigidez
secante propuesta por Jennings (1968).
El ATC-40 al considerar las imperfecciones de las curvas de histéresis, en el sentido
de que no son rectas como se ha considerado en el modelo bilineal sino curvas, introduce un
factor de corrección , el mismo que se indica en la figura 7.6. De tal manera que el
amortiguamiento viscoso efectivo, es:
eq
eq
En la figura 7.6, se aprecian tres curvas para determinar el factor de corrección ,
las mismas que corresponden a tres categorías de comportamiento estructural. La Tipo A, tiene
un comportamiento estable y perfectamente histerético. La tipo C, es para estructuras con un
pobre comportamiento histerético que corresponden a estructuras con mal comportamiento
sísmico y la Tipo B, es para un caso intermedio.
En la figura 7.6, se aprecia que el ATC-40 considera 1
, para un eq
menor a
0.15 para las estructuras tipo A. Para las tipo B, el factor es 0.667 para un amortiguamiento
viscoso equivalente menor a 0.25 y para las estructuras tipo C, el factor es 0.333 lo que implica
una considerable reducción en el área del diagrama de histéresis. Por otra parte, el valor eq
tiene que ser menor a 0.45.
(7.12)
(7.13)
(7.14)
( 7.15)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-259-320.jpg)





![SISTEMAS DE UN GRADO DE LIBERTAD
254
La excitación
wt
sen
F
t
f 0
)
( . Donde 0
F es la amplitud máxima de la fuerza )
(t
f y
w la frecuencia de la excitación. La ecuación diferencial a resolver es:
t
w
sen
F
t
q
k
t
q
c o
)
(
)
(
.
Figura 7.10 Excitación armónica
Si se considera ; en la solución de la ecuación diferencial que se presentó en el
capítulo 1, se tiene que la solución permanente vale:
t
sen
C
K
F
t
q o
2
2
)
(
El ángulo de fase es:
K
C
tg
1
Luego la velocidad )
(
.
t
q se obtiene con la siguiente ecuación:
t
C
K
F
t
q o
cos
)
(
2
2
.
La fuerza )
(t
f es:
t
sen
C
K
F
K
t
C
K
F
C
t
f
t
q
K
t
q
C
t
f
2
2
0
2
2
0
.
cos
)
(
)
(
)
(
)
(
El programa kelvin reporta las curvas de histéresis para el modelo de Kelvin Voight.
[q] = kelvin(K,C,Fo,w)
K Es la rigidez del oscilador.
C Es el amortiguamiento.
Fo Es la máxima fuerza de la excitación armónica.
Es la frecuencia de la excitación.
El programa reporta la curva de histéresis y el desplazamiento máximo.
function [qmax]=kelvin(k,c,Fo,w)
%
% Curva de histeresis de un oscilador Kelvin-Voight
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
% Agosto de 2006
(7.22)
(7.23)
(7.20)
(7.21)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-265-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
255
%------------------------------------------------------------------
% [qmax]=kelvin(k,c,Fo,w)
%------------------------------------------------------------------
% k : rigidez del oscilador kelvin-voight
% c : amortiguación del oscilador kelvin-voight
% Fo: Amplitud máxima de excitación Fo Sen (wt)
% w : Frecuencia de la excitación
% dt : incremento de tiempo con el cual se calcula la respuesta.
% q : Respuesta en desplazamientos.
% Ft: Fuerza en el tiempo
%
tmax=10; n=1000; t=linspace(0,tmax,n)';
% Calculo de fi
if k==0
fi=0;
else
fi=atan(c*w/k);
end
% Respuesta en desplazamientos
den1=k*k+(c*c*w*w); coef1=Fo/sqrt(den1);
for i=1:n
q=coef1*sin(w*t+fi);
end
qmax=max(abs(q));
% Respuesta en fuerzas
coef2=(Fo*c*w)/sqrt(den1); coef3=(Fo*k)/sqrt(den1);
for i=1:n
Ft=coef2*cos(w*t+fi)+coef3*sin(w*t+fi);
end
plot (q,Ft)
ylabel('Fuerza');xlabel('Desplazamiento')
%---fin---
EJEMPLO 3
Encontrar las curvas de histéresis para el modelo de Kelvin Voight, para los siguientes
casos:
i. 0
20
C
cm
kg
K
ii.
cm
s
Kg
C
cm
kg
K 45
.
0
20
iii.
cm
s
Kg
C
cm
kg
K 0
.
2
20
iv.
cm
s
Kg
C
K 45
.
0
0
En todos los casos la fuerza
t
sen
t
f
80
)
(
SOLUCIÓN
Para resolver el ejemplo se utilizó el programa kelvin se deja al lector interpretar las
curvas de histéresis presentadas en la figura 7.11.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-266-320.jpg)



![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
259
2 ̇ ̇ ̇ ̇
̇ ̇
3
Luego de elevar al cuadrado y factorar, se tiene:
2 ̇ ̇ ̇ ̇ . / ̇ . / ̇ ( ) ̇ ̇ 3
De donde la matriz de amortiguamiento es la siguiente:
[ ]
EJEMPLO 6
Resolver el Ejemplo 5, con las coordenadas presentadas en la figura 7.15. Se recuerda
que las columnas de la planta baja son axialmente rígidas y que las dos vigas son totalmente
rígidas.
Figura 7.15 Estructura y grados de libertad de Ejemplo 6
SOLUCIÓN
Se recomienda al lector que haga las deformadas elementales y encuentre le
desplazamiento vertical en el punto “a” con estas nuevas coordenadas. Este desplazamiento
resulta.
{ ̇ ̇ ̇ 0 ̇ ̇ 1 }](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-270-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
260
[
( )
( ) ]
EJEMPLO 7
A la izquierda de la figura 7 se presenta el sistema de coordenadas con que se obtuvo
la matriz de amortiguamiento en el Ejemplo 5; se denomina a esta matriz . A la derecha de la
figura 7 se indica el sistema de coordenadas para el cual se halló la matriz de amortiguamiento
en el Ejemplo 6. Se han denominado a estos dos sistemas “Q-q” y “Q
*
-q
*
”. Se pide encontrar la
matriz de paso , tal que: , y comprobar que la matriz de amortiguamiento en el
sistema “Q
*
-q
*
” que se va a denominar , se halla de la siguiente manera:
Siendo la matriz de amortiguamiento en el sistema “Q-q”
Sistema Q-q Sistema Q
*
-q
*
Figura 7.16 Dos sistemas de coordenadas para Ejemplo 7.
SOLUCIÓN
La matriz de paso , resulta:
[ ]
Se recuerda que la matriz de paso se halla construyendo deformadas elementales en
el sistema y midiendo las deformaciones en el sistema .
Al realizar el triple producto matricial , con la matriz del Ejemplo 5, se halla la
matriz de amortiguamiento encontrada en el Ejemplo 6.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-271-320.jpg)



![SISTEMAS DE UN GRADO DE LIBERTAD
264
SOLUCIÓN
Los valores propios, son 9323
.
61
1
y 0970
.
562
2
, y los vectores propios son:
01731
.
0
03351
.
0
03747
.
0
01548
.
0
2
1
0
.
1
0
.
1 2
2
2
1
1
1
M
M
M
M t
t
Modo 1
7870
.
0
1
8697
.
7
05
.
0
2
2
8697
.
7
9323
.
61
1
1
1
1
M
W
W n
n
Al aplicar la ecuación (7.41) se obtiene:
6911
.
380
6778
.
196
6778
.
196
6104
.
101
1
C
Modo 2
3709
.
2
1
7086
.
23
05
.
0
2
2
7086
.
23
0970
.
562
2
2
2
2
M
W
W n
n
8089
.
244
5193
.
592
5193
.
592
0948
.
1434
2
C
Finalmente, al sumar las dos matrices de amortiguamiento, se obtiene:
4999
.
625
8415
.
395
8415
.
395
7052
.
1535
C
Nótese en este ejemplo que la contribución del modo dos es más importante en valores
que la contribución del modo uno.
El programa denominado amortiguamiento_1 obtiene la matriz de amortiguamiento de
una estructura utilizando el algoritmo de Wilson y Penzien. Para su uso en la modalidad
consola el usuario debe indicar la matriz de rigidez y el vector zeda que contiene los factores
de amortiguamiento , tantos como el orden de la matriz de rigidez. La forma de uso, es:
>> [C]=amortiguamiento_1 (K,zeda)
K es la matriz de rigidez.
zeda vector que contiene los factores de amortiguamiento.
Posteriormente por pantalla se indican las masas de cada piso.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-275-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
265
function [C]=amortiguamiento_1 (K,zeda)
%
% Calculo de la matriz de amortiguamiento utilizando
% Algoritmo de Wilson y Penzien
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
% -----------------------------------------------------------------
% [C]=amortiguamiento_1 (K,zeda)
% -----------------------------------------------------------------
% K Matriz de rigidez lateral del portico plano.
% M Matriz de masas.
% NP Número de pisos.
% Por pantalla se indicara las masas de cada piso.
% Previamente el usuario habra calculado la matriz de rigidez lateral
% con otro programa.
% T Periodos de vibracion.
% C Matriz de amortiguamiento.
% zeda Vector que contiene los coeficientes de amortiguamiento.
%
NP = input (' n Numero de pisos ');
M = zeros(NP,NP); C = zeros(NP,NP);
for i=1:NP
fprintf ('Indique la masa del piso , %2d',i);
M(i,i) = input (', Valor de la masa: ');
end
[V,D]=eig(K,M); Wn=sqrt(D); W=diag(Wn);
for i=1:NP
fi=V(:,i); mi=fi'*M*fi; aux=2*zeda(i)*W(i)/mi;
C=C+aux.*M*fi*fi'*M;
end
fprintf ('n Matriz de amortiguamiento')
C
% ---fin
EJEMPLO 10
Ilustrar la forma de uso del programa amortiguamiento_1 con los datos del Ejemplo 9.
SOLUCIÓN
>> K = [348000 -125000; -125000 88000]
>> zeda =[0.05; 0.05]
>> [C] = amortiguamiento (K,zeda)
Número de pisos 2
Indique la masa del piso, 1, Valor de la masa: 734
Indique la masa del piso, 2, Valor de la masa: 587
REPORTE DE PROGRAMA
Matriz de amortiguamiento
C =
1.0 e+003 *
1.5357 -0.3958
-0.3958 0.6255](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-276-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
266
7.5 PROGRAMA amortiguamiento
En lugar de encontrar la contribución de cada uno de los modos a la matriz de
amortiguamiento y luego sumarlos se puede calcular la matriz de amortiguamiento
directamente con la siguiente ecuación:
M
C
M
C t
d
Donde C es la matriz de amortiguamiento de la estructura; es la matriz de masas; es la
matriz modal cuyas columnas son los modos de vibración
)
(i
; d
C es una matriz diagonal
cuyos elementos valen
)
(
)
(
)
(
)
(
/
2 i
t
i
i
n
i
M
W
, siendo
)
(i
el factor de amortiguamiento
en el modo de vibración i;
)
(i
n
W la frecuencia natural de vibración en el modo i;
)
(i
es el
modo de vibración en el modo i. Es conveniente encontrar los modos
)
(i
normalizados de tal
manera que el triple producto matricial 1
)
(
)
(
i
t
i
M
.
El programa amortiguamiento que se presenta a continuación encuentra la matriz de
amortiguamiento mediante la ecuación (7.42).
function [C]=amortiguamiento(M,phi,OM,zeda)
%
% Programa para encontrar la matriz de amortiguamiento de una estructura
% Amortiguamiento tipo Wilson y Penzien
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2009
%-------------------------------------------------------------
% [C]=amortiguamiento(M,phi,OM,zeda)
%-------------------------------------------------------------
% M Matriz de masa de la estructura
% phi Matriz que contiene los modos de vibración normalizados
% OM Vector que contiene las frecuencias de vibración de menor a mayor.
% ngl Número de grados de libertad
% zeda Factor de amortiguamiento de la estructura, un solo valor
n=length(M(:,1));
ZEDA=zeros(n);for i=1:n; ZEDA(i,i)=zeda; end
mms=diag(phi'*M*phi); % mms es un vector unitario
Cd=zeros(n);for i=1:n; Cd(i,i)=2*ZEDA(i,i)*OM(i)/mms(i); end
C=M*phi*Cd*phi'*M;
return;
end
7.6 ECUACIONES DIFERENCIALES DESACOPLADAS
En el algoritmo de Wilson y Penzien, se empezó indicando que:
M
C
C
t
2
Para demostrar esta ecuación, es necesario explicar el desacoplamiento del sistema de
ecuaciones diferenciales. Para ello, se recurre al sistema de ecuaciones diferenciales que
gobiernan los problemas dinámicos. Esta es:
(7.42)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-277-320.jpg)







![SISTEMAS DE UN GRADO DE LIBERTAD
274
Se halla el exponencial de
t
F
e
Finalmente se encuentra la respuesta )
(t
X mediante la ecuación (7.67).
El programa vlibreamortiguado, resuelve el problema de vibraciones libres en un
sistema de múltiples grados de libertad considerando el amortiguamiento. La forma de uso del
programa es la siguiente:
[q]=vlibreamortiguado(K, zeda, Xo)
K es la matriz de rigidez lateral de la estructura, la misma que deberá indicarse en
consola.
zeda es el vector que contiene los factores de amortiguamiento. Si el sistema tiene n
grados de libertad, se deberán indicar n valores de .
Xo es el vector de condiciones iniciales, que contiene los desplazamientos y
velocidades del sistema. El orden de este vector es 2n; los n primeros valores
corresponden a los desplazamientos y los n restantes a las velocidades en 0
t .
function [q]=vlibreamortiguado(K,zeda,Xo)
%
% Vibraciones libres considerando amortiguamiento.
% Solucion por medio del exponencial de una matriz.
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
% -----------------------------------------------------------------
% [q]=vlibreamortiguado(K,zeda,Xo)
% -----------------------------------------------------------------
% K Matriz de rigidez lateral del portico plano, viene de consola.
% M Matriz de masas.
% NP Numero de pisos, igual al número de grados de libertad.
% Por pantalla se indicara las masas de cada piso.
% Previamente el usuario habra calculado la matriz de rigidez lateral
% con otro programa.
% T Periodos de vibracion.
% C Matriz de amortiguamiento.
% zeda Vector que contiene los coeficientes de amortiguamiento. viene de
% consola, sirve para calcular matriz de amortiguamiento.
% Xo Vector de condiciones iniciales, viene de consola.
% F Matriz de orden 2nx2n
% q Los n primeros valores corresponden a los desplazamientos y los
% restantes a las velocidades.
% dt Incremento de tiempo con el cual se obtiene la respuesta.
% n Número de puntos que se desean obtener en la respuesta.
% Programado para dt=0.02 y n=100
dt=0.02; n=100;
NP = input (' n Numero de pisos ');
M = zeros(NP,NP); C = zeros(NP,NP);
% Matriz de Masas
for i=1:NP
fprintf ('Indique la masa del piso , %2d',i);
M(i,i) = input (', Valor de la masa: ');
end
% Matriz de amortiguamiento mediante algoritmo de Wilson y Penzien
[V,D]=eig(K,M); Wn=sqrt(D); W=diag(Wn);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-285-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
275
for i=1:NP
fi=V(:,i); mi=fi'*M*fi; aux=2*zeda(i)*W(i)/mi;
C=C+aux.*M*fi*fi'*M;
end
% Matriz F
CERO=zeros(NP,NP); IDENT=eye(NP,NP);MIK=(-1)*inv(M)*K; MIC=(-1)*inv(M)*C;
F=[CERO IDENT; MIK MIC];
% Valores Propios de F
[V,D] = eig(F)
% Respuesta en el tiempo
for j=1:n
t=j*dt; E=expm(F*t); EE=real(E); q=EE*Xo;
tt(j)=t; des(j)=q(NP);
end
% Dibujo para la respuesta en el tiempo del último piso
plot (tt,des)
xlabel ('Tiempo (s)'); ylabel ('Desplazamiento ultimo piso');
title ('Vibracion libre considerando amortiguamiento');
% ---fin
EJEMPLO 12
Encontrar la respuesta en el tiempo, para el tercer piso, de la estructura indicada en la
figura 7.18, cuyas matrices de rigidez y masa, son:
633
.
1
0
0
0
633
.
1
0
0
0
633
.
1
9
.
836
6
.
1080
7
.
285
6
.
1080
0
.
2278
1
.
1538
7
.
285
1
.
1538
1
.
2761
M
K
Para los siguientes casos:
i) En t=0 ; los desplazamientos laterales son 1.0 cm., para el primer piso; 2.0 cm.,
para el segundo piso y 3.0 cm., para el tercer piso. Las velocidades son nulas para
t=0.
ii) En t=0; únicamente el desplazamiento del tercer piso vale 3.0 cm. Las velocidades
son nulas.
Para los dos casos los valores de 05
.
0
3
2
1
Esta estructura fue analizada en el capítulo 6, cuando se hallaron los modos de
vibración.
SOLUCIÓN
Los vectores de condiciones iniciales, para los dos casos que se van a analizar, son:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-286-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
276
0
0
0
03
.
0
0
0
0
0
0
03
.
0
02
.
0
01
.
0
0
0 X
X
Figura 7.18 Pórtico plano sometido a dos ensayos de vibración libre.
Se detalla el cálculo para el primer caso, con el programa vlibreamortiguado
>> K=[2761.1 -1538.1 285.7; -1538.1 2278.0 -1080.6; 285.7 -1080.6 836.9];
>> zeda=[0.05; 0.05; 0.05];
>> Xo=[0.01; 0.02; 0.03; 0; 0; 0];
>> [q]=vlibreamortiguado(K,zeda,Xo)
Número de pisos 3
Indique la masa del piso, 1, Valor de la masa: 1.633
Indique la masa del piso, 2, Valor de la masa: 1.633
Indique la masa del piso, 3, Valor de la masa: 1.633
La respuesta, para los desplazamientos laterales del tercer piso se indica en la figura
7.19. El programa vlibreamortiguado encuentra la respuesta en el tiempo para un incremento
de tiempo de 0.02 s., y hasta un tiempo de 2 s., si se desea la respuesta para un incremento de
tiempo menor se debe cambiar dt en el programa. De igual forma si se desea calcular para un
mayor tiempo se debe cambiar n.
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
3
3
3
4 4](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-287-320.jpg)














![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
291
Figura 8.2 Modelo de cálculo de un pórtico plano para el análisis sísmico.
SOLUCIÓN
Para el análisis sísmico plano, en que se concentran las masas, como se indica en la
figura 8.2, el vector J es unitario. Para encontrar las matrices de rigidez, masas y
amortiguamiento, las unidades utilizadas son T., m., y s. Esto se debe tener cuenta para que el
acelerograma tenga unidades de m/s
2
.
Para resolver el problema se elaboró el programa newmarklineal y la forma de uso es
la siguiente:
[Y] = newmarlineal (p,M,C,K,J,dt,beta)
p Corresponde al nombre del archivo que contiene el acelerograma.
M Es la matriz de masas de orden (nxn) Siendo n el número de grados de libertad.
C Es la matriz de amortiguamiento.
K Es la matriz de rigidez.
J Es el vector unitario, para el caso plano (Q = - M J a(t) ).
dt Es el incremento de tiempo del acelerograma y con el cual se halla la respuesta
dinámica.
beta Vale 0.25 cuando se considera aceleración constante o 0.167 para aceleración
lineal.
Y Es la respuesta máxima de los desplazamientos, en valor absoluto, del
último piso de un pórtico plano.
>> K=[2761.1 -1538.1 285.7; -1538.1 2278.0 -1080.6; 285.7 -1080.6 836.9]
>> M=[1.63 0 0; 0 1.63 0; 0 0 1.63]
>> C=[ 6.3608 -2.1516 0.0124; -2.1516 5.3010 -2.1143; 0.0124 -2.1143 3.0325]
>> J=[1; 1; 1]
>> load Peru04.dat
>> [Y] =newmarklineal (Peru04,M,C,K,J,0.02,0.167)
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
30x30
3
3
3
4 4](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-302-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
292
El archivo del acelerograma tiene un 02
.
0
dt y se ha considerado 167
.
0
. La
respuesta del tercer piso se indica en la figura 8.3 y el valor máximo del desplazamiento es
0.0226 m. Este ejercicio se resuelve también, más adelante, por el Procedimiento de Espacio
de Estado.
function [ymax]=Newmarklineal(p,M,C,K,J,dt,beta)
% Respuesta en el tiempo de un sistema de multiples grados de libertad
% por el Metodo de Newmark, ante una sismo definido por su acelerograma
%
% Por: Roberto Aguiar Falconi
% 27 de enero de 2015
%------------------------------------------------------------------
% [ymax]=Newmarklineal(p,M,C,K,J,dt,beta)
%------------------------------------------------------------------
% p : vector que contiene los registros del acelerograma en gals
% M : matriz de masas del sistema (T s2/m)
% C : matriz de amortiguamiento del sistema (T s/m)
% K : matriz de rigidez del sistema (T/m)
% J : Q=-M J a(t) es vector unitario para caso plano.
% dt : incremento de tiempo con el cual se calcula la respuesta.
% beta: Vale 1/4 para aceleracion constante, 1/6 para aceleracion lineal,
% 1/8 escalonada
% gama: Vale 0.5
% d, v, a : desplazamiento, velocidad y aceleracion de la respuesta
%
% El programa solo guarda el corrimiento en ultimo piso
n=length(p);tmax=dt*n;t=linspace(0,tmax,n)';gama=0.5;ngl=length(K);
% Cambio de cm/s2 a m/s2 en el acelerograma
for i=1:n
p(i)=p(i)/100;
end
% Constantes auxiliares de cálculo
fac1=1/(beta*dt);fac2=gama/(beta*dt); fac3=1/(beta*dt*dt);
fac4=(1/(2*beta))-1;fac5=1-(gama/beta); fac6=1-(gama/(2*beta));
% Calculo de K sombrero
Ks=K+fac3*M+fac2*C;
% Condiciones iniciales nulas
for i=1:ngl
d(i)=0; v(i)=0; a(i)=0;
end
d=d';v=v';a=a';
% Respuesta en el tiempo
for i=1:n-1
F=-M*J*p(i+1)+M*(fac1*v+fac4*a)-C*(fac5*v+fac6*dt*a)-K*d;
dq=KsF;aa=fac3*dq-fac1*v-fac4*a;
vv=fac2*dq+fac5*v+fac6*dt*a;dd=dq+d;
y(i)=dd(ngl);tt(i)=dt*i; % Desplazamiento en ultimo piso
y1(i)=dd(1); % Desplazamiento del primer piso
d=dd; v=vv; a=aa;
end
plot (tt,y)
ylabel('Desplazamiento ultimo piso');xlabel('Tiempo')
ymax=max(abs(y))
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-303-320.jpg)







![SISTEMAS DE UN GRADO DE LIBERTAD
300
factor de reducción de las fuerzas sísmicas R , que es función del factor de reducción por
ductilidad
R , del factor de resistencia s
R y del factor de redundancia . Aguiar, (2007)
Figura 8.15 Variación en el tiempo del cortante basal.
8.5 PROCEDIMIENTO DE ESPACIO DE ESTADO
El Procedimiento de Espacio de Estado, SSP, es muy utilizado para encontrar la
respuesta en el tiempo de estructuras y es muy apropiado para trabajar con matrices de
rigidez, masa y amortiguamiento que no son diagonales. El Procedimiento de Espacio de
Estado, tiene enormes ventajas de exactitud y tiempo de ejecución respecto a métodos
clásicos. Además de ello no presenta problemas de estabilidad en la solución numérica.
8.5.1 Formulación del Problema
El sistema de ecuaciones diferenciales que gobiernan los problemas de dinámica
estructural, fue indicado en la ecuación (8.12) sin embargo para tenerlo presente se vuelve a
repetir la mencionada ecuación. De igual manera se repite la obtención de la matriz y de la
ecuación de estado que se presentó en el capítulo anterior.
̈ ̇
Donde son las matrices de masa, amortiguamiento y rigidez, respectivamente;
̇ ̈ son los vectores de desplazamiento, velocidad y aceleración. es el vector de cargas
generalizadas.
Al premultiplicar la ecuación por
1
M , por la izquierda, se halla:
Q
M
q
K
M
q
C
M
q 1
1
.
1
..
Como artificio numérico de cálculo se introduce la siguiente ecuación:
̇ ̇
Se introduce la siguiente notación:
* ̇ + ̇ [
̇
̈
]
Con esta notación, las ecuaciones (8.21) y (8.20), quedan:
-2
0
2
4
6
8
10
12
14
16
0 5 10 15 20
Tiempo (Seg)
Cortante
Basal
(Ton)
(8.20)
(8.21)
(8.22)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-311-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
302
Al discretizar la respuesta y considerando un incremento constante de tiempo t
se
puede encontrar la respuesta en un instante t
k
t
1 en función del valor anterior para
t
k
t
0 .
t
k
t
k
d
r
F
t
k
t
k
X
t
F
t
t
k
X
1
1
exp
exp
Se considera que la variación de la excitación r entre el instante de tiempo t
k y el
instante de tiempo t
k
1 es lineal. Luego:
t
k
t
k
t
t
k
r
t
t
k
r
t
k
t
k
r
r
1
Al sustituir esta variación de
r en la integral y considerando el siguiente cambio de
variable:
d
d
t
k
1
Se tiene:
t
d
t
k
r
t
t
k
r
t
t
k
r
t
F
t
k
X
t
F
t
t
k
X
0
exp
exp
Ecuación que puede expresarse en forma condensada, de la siguiente manera:
k
r
k
r
P
k
r
P
k
X
A
k
X
1
1
1 2
1
Donde:
A
P
t
F
P
I
A
F
P
e
A F
t
1
1
2
1
1
1
El algoritmo de Espacio de Estado puede ser considerado como la generalización de la
integral de Duhamel (Capítulo 1) para varios grados de libertad.
8.5.4 Programa pse
El programa pse encuentra la respuesta en el tiempo de un sistema de n grados de
libertad ante una acción sísmica definida por un acelerograma. La forma de uso del programa
es la siguiente:
[q]=pse(M,C,K,Qo,p,dt)
M es la matriz de masas del sistema, de orden nXn. El usuario debe indicar por consola
esta matriz.
C es la matriz de amortiguamiento del sistema, que debe el usuario dar por consola.
K es la matriz de rigidez del sistema, que debe el usuario dar por consola.
Qo es el vector que multiplica a la aceleración del suelo, se debe indicar por consola.
p es el nombre del archivo que contiene al acelerograma.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-313-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
303
dt es el incremento de tiempo del acelerograma. Con este incremento de tiempo se
encuentra la respuesta en el tiempo.
Si se tiene un sistema de un grado de libertad, la ecuación del movimiento es:
)
(
.
..
t
a
m
q
k
q
c
q
m
Para este caso el valor de Qo que se debe indicar al programa es: Qo=[-m]
Para un sistema de múltiples grados de libertad, el sistema de ecuaciones diferenciales
es el siguiente:
)
(
.
..
t
a
J
M
q
K
q
C
q
M
En este caso el valor de Qo es: J
M
Q
0
Como se aprecia Qo es el vector que multiplica a la aceleración del suelo )
(t
a . Es
importante tener presente las unidades en las cuales está el acelerograma. Si las unidades
están en cm./s
2
, en el cálculo de las matrices de masa, rigidez y amortiguamiento se deberá
trabajar con T., y cm., como se aprecia en el primer ejemplo que se resuelve, posteriormente.
Si en todo el cálculo dinámico se ha trabajado en T., y m., el usuario del programa
debe cambiar las unidades del acelerograma de cm./s
2
a m/s
2
. Esto antes de utilizar el
programa pse, la otra opción es modificar al programa de tal manera que la aceleración del
suelo se pase de cm./s
2
., a m/s
2
.; este procedimiento se ilustra en el segundo ejemplo. Lo
importante es que se tengan unidades compatibles.
function [q]=pse(M,C,K,Qo,p,dt)
%
% Procedimiento de Espacio de Estado para sistemas de n grados de libertad
% Programa general en que se requiere la respuesta ante un acelerograma.
%
% Por: Roberto Aguiar Falconi
% CEINCI ESPE
% -----------------------------------------------------------------
% [q]=pse(M,C,K,Qo,p,dt)
% -----------------------------------------------------------------
% M Matriz de masas.
% C Matriz de amortiguamiento.
% K Matriz de rigidez.
% Qo Coeficiente del vector de cargas que multiplica a la aceleración
% del suelo.
% p Acelerograma para el cual se calcula la respuesta en el tiempo.
% Previamente el usuario habrá calculado las matrices de masa,
% amortiguamiento, rigidez, así como el coeficiente Qo.
% F Matriz de orden 2nx2n
% q Los n primeros valores corresponden a los desplazamientos y los
% restantes a las velocidades.
% dt Incremento de tiempo con el cual se obtiene la respuesta.
ngl=length(K);
% Matriz F
CERO=zeros(ngl,ngl); IDENT=eye(ngl,ngl);MIK=(-1)*inv(M)*K;MIC=(-1)*inv(M)*C;
F=[CERO IDENT; MIK MIC];
% Exponencial de la matriz F multiplicado por dt
A=expm(dt*F);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-314-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
304
% Matrices P1 y P2
IDEN=eye(2*ngl,2*ngl); P1=inv(F)*(A-IDEN); P2=inv(F)*((1/dt)*P1-A);
% Vector r de cargas sísmicas
for i=1:ngl; NULO(i)=0; end; MIQ=inv(M)*Qo;
% respuesta en el tiempo
n=length(p);
for i=1:2*ngl; Xk(i)=0;end; Xk=Xk';q=Xk(ngl);
for i=1:n-1
t(i)=i*dt;
MCARGA=MIQ*p(i); MCARGA2=MIQ*p(i+1);rk=[NULO'; MCARGA];rk2=[NULO'; MCARGA2];
Xk2=A*Xk+P1*rk2+P2*(rk2-rk);
% Solo almacena la respuesta en el tiempo del ultimo grado de libertad
q(i)=Xk2(ngl); Xk=Xk2;
end
q=q'; t=t';
% Dibujo para la respuesta en el tiempo del ultimo piso
plot (t,q)
xlabel ('Tiempo (s)'); ylabel ('Desplazamiento ultimo piso');
% ---fin
EJEMPLO 5
Encontrar la respuesta en el tiempo de un sistema de 1 gdl., que está definido por:
cm
T
k
cm
T
c
cm
s
T
m 193366
.
0
0030775
.
0
004898
.
0
2
Ante el sismo registrado en el Perú el 9 de noviembre de 1974, cuyo archivo está en
gals y se denomina Peru04.dat. El intervalo de tiempo de este archivo es 0.02 s. (Este ejercicio
fue resuelto en el capítulo 2).
SOLUCIÓN
En la figura 8.16 se presenta la respuesta en el tiempo del sistema, pero antes se
indica la forma como se debe proceder para la entrada de datos, para utilizar el programa.
>> M=[0.004898]
>> C=[0.003775]
>> K=[0.193366]
>> Qo=[-0.004898]
>> load Peru04.dat
>> [q]=pse(M,C,K,Qo,Peru04,0.02)
Las matrices ,
,
,
,
, 2
1
1
P
P
A
F
F
son:
0
1
0253
.
0
0159
.
0
6283
.
0
4786
.
39
1
0 1
F
F
9797
.
0
7826
.
0
0198
.
0
9921
.
0
A
0099
.
0
0052
.
0
0001
.
0
010
.
0
0198
.
0
0079
.
0
0002
.
0
0199
.
0
2
1 P
P](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-315-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
306
Figura 8.17 Desplazamientos del tercer piso de ejemplo 2.
Los desplazamientos laterales máximos, para cada uno de los pisos y el cálculo de la
deriva máxima de piso se indican en la tabla 8.2. La deriva máxima de piso es el
desplazamiento relativo de piso dividido para la altura de piso.
Tabla 8.2 Cálculo de la deriva máxima de piso
Piso Desplazamiento
Máximo
(m)
Desplazamiento
Relativo
(m)
Altura de Piso
(m)
Deriva de Piso
(%)
3 0.0227 0.0063 3.00 0.21
2 0.0164 0.0092 3.00 0.31
1 0.0072 0.0072 3.00 0.24
En la última columna de la tabla 8.2 se indica la deriva máxima de piso en porcentaje.
Interesa el mayor valor de todos ellos. Este es 0.31%.
8.5.5 Segunda forma de solución
Para la segunda forma de cálculo, en la ecuación (8.25) se remplaza ,
con lo que se obtiene.
[ ]
La solución es la misma presentada en la ecuación (8.26) pero escrita de otra manera.
Donde:
C
M
K
M
I
F 1
1
0
(8.32)
(8.33)
(8.34)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-317-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
307
[ ]
El programa que encuentra la respuesta en el tiempo de la forma indicada en este
apartado se denomina pee_de_uno. Este programa para cada valor de la aceleración del suelo
encuentra la respuesta en el tiempo. En el capítulo 6 se presentó este programa.
Figura 8.18 Estructura de un piso con aislador de base.
8.6 AISLADORES DE BASE ELASTOMÉRICOS CASO PLANO
En el capítulo 5, se presentó el marco teórico para el caso de una estructura de un piso
con aisladores de base elastoméricos; en la figura 8.18 se muestra el modelo numérico de
análisis y se va a volver a presentar las ecuaciones diferenciales, con el propósito de entender
bien el modelo y poder generalizarlo para pórticos de varios pisos.
* + [
̈
̈
] [ ] [
̇
̇
] [ ] * + * + * +
El significado de las variables está indicado en forma gráfica en la figura 8.18. Al
desarrollar el sistema de ecuaciones diferenciales se encuentra.
̈ ̈ ̇
̈ ̈ ̇
Se denomina:
Con lo que las ecuaciones diferenciales quedan de la siguiente forma.
:
̈ ̇ ̈
̈ ̇ - ̈
La ecuación (8.35) corresponde al sistema de aislación y la (8.36) a la superestructura,
que en este caso es de un piso. Generalizando lo presentado para pórticos planos con
aisladores de base elastoméricos, y en lugar de denominar a la coordenada del aislador
se la denomina a secas y a las coordenadas laterales de la superestructura se las llama con
la letra ; se tiene:
̈ ̇ ̈
̈ ̇ [ ̈]
(8.35)
(8.36)
(8.37)
(8.38)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-318-320.jpg)




![SISTEMAS DE UN GRADO DE LIBERTAD
312
de la figura 8.21. A la derecha de 8.22 se presentan los grados de libertad, considerando que
las vigas son axialmente rígidas. Se tienen 10 grados de libertad; interesa conocer la reacción
vertical y la . Se utiliza este modelo para calcular directamente las reacciones, caso
contrario se debió emplear un modelo con empotramiento en el sitio donde van los aisladores.
El sistema de coordenadas indicado a la derecha de la figura 8.22 está
compuesto por coordenadas “a” y “b”. Las coordenadas “a” son aquellas cuyo desplazamiento
es cero para el cálculo de las reacciones. . Las coordenadas “b” van de la 6 a la 10.Con
esta acotación la ecuación básica de análisis estático se escribe de la siguiente manera.
b
BB
BA
AB
AA
b
a
q
K
K
K
K
Q
Q
R
q
K
Q
0
Donde R es el vector que contiene a las reacciones de la estructura; a
Q es el vector
de cargas asociado a las coordenadas a (apoyos); b
Q es el vector de cargas de la estructura
como que si estuviera empotrada en la base. Al desarrollar los productos matriciales se halla:
b
BB
b
b
AB
a
q
K
Q
q
K
Q
R
Figura 8.22 Modelo para el cálculo de las reacciones de la superestructura.
Luego el procedimiento de cálculo para encontrar las reacciones es el siguiente:
i. Encontrar la matriz de rigidez de toda la estructura, utilizando todos los programas de
CEINCI-LAB que se han indicado en los capítulos anteriores de este libro. Particionar
esta matriz y hallar las submatrices que están indicadas en la ecuación (8.47).
ii. Encontrar el vector de cargas , que contiene a: . Para el efecto se debe utilizar
el programa cargas.
iii. Particionar y hallar: .
iv. Resolver el sistema de ecuaciones , y encontrar .
v. Calcular con la primera ecuación de (8.48)
A continuación se indica el programa cargas, se deja al lector que vea la entrada de datos.
function [Q,Q2]=cargas(njc,nmc,ngl,L,seno,coseno,CG,VC,F,Fm)
%
% Programa que calcula el vector de cargas Q de un pórtico plano
(8.47)
(8.48)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-323-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
313
% con cargas en los elementos y en las juntas
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Octubre de 2009
%-------------------------------------------------------------
% [Q,Q2]=cargas(njc,nmc,ngl,L,seno,coseno,CG,VC,F,Fm)
%-------------------------------------------------------------
% njc número de juntas cargadas
% nmc número de miembros cargados
% ngl número de grados de libertad
% L Vector que contiene la longitud de los elementos
% seno Vector que contiene el seno de cada elemento
% coseno Vector que contiene el coseno de cada elemento
% VC Matriz de vectores de colocación de elementos
% F Matriz con: Nudo cargado, FH, FV, Momento
% Fm Matriz con: Núm elem, Carga, Código, elem a gener, incr. num elem.
% Código=1 Carga Uniforme en elemento horizontal
% Código=2 Carga Triangular en elemento horizontal
%
% Q Vector de cargas generalizadas
% Q2 Matriz con Vectores de empotramiento perfecto en
% coordenadas locales de todos los elementos
% CARGAS EN JUNTAS
Q=zeros(ngl,1);ic=length(VC(1,:));mbr=length(L);
Q2=zeros(mbr,ic);% Empotramiento perfecto en coord. locales.
if njc~=0
for i=1:njc
nudo=F(i,1);
for j=1:3
gdl(j)=CG(nudo,j);Q(gdl(j))=F(i,j+1);
end
end
end
% CARGAS EN LOS ELEMENTOS
if nmc~=0
nf=length(Fm(:,5));
for icon=1:nf
i=Fm(icon,1); % Numero de elemento cargado
P=Fm(icon,2); % Carga en elemento
icod=Fm(icon,3); % Código del tipo de carga
ielem=Fm(icon,4); % Elementos a generar con igual carga y longitud
icr=Fm(icon,5); % Incremento en la numeración de elementos con igual carga
if icod==1 & seno(i)==0 % CARGA UNIFORME EN ELEMENTO HORIZONTAL
Q2(i,2)=P*L(i)/2;Q2(i,5)=Q2(i,2);
Q2(i,3)=P*L(i)*L(i)/12;Q2(i,6)=-Q2(i,3);
elseif icod==1 & seno(i)~=0 % CARGA UNIFORME EN ELEMENTO INCLINADO
Px=P*seno(i)*coseno(i);Py=P*coseno(i)*coseno(i);
dx=L(i)/100;
for k=1:100
x(k)=(k-1)*dx;fac=x(k)/L(i);
f1(k)=(1-fac)*Px; %Funcion de forma fi1 * Px
f2(k)=(1-3*fac^2+2*fac^3)*Py; %Funcion de forma fi2 * Py
f3(k)=(x(k)*(1-fac)^2)*Py; % Funcion de forma fi3 * Py
f4(k)=fac*Px; %Función de forma fi4 * Px
f5(k)=(3*fac^2-2*fac^3)*Py; % Funcion de forma fi5 * Py
f6(k)=(-x(k)^2/L(i))*(1-fac)*Py; % Funcion de forma fi6 * Py](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-324-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
315
en coordenadas locales, que se encuentra con la siguiente ecuación.
[ ]
Donde es la rigidez horizontal del aislador; es la rigidez vertical del aislador. La
rigidez horizontal ya se indicó como se obtiene; la rigidez vertical se halla en función del área
de las placas, del módulo de compresión para el conjunto goma-acero y de la altura total de
goma del aislador.
Figura 8.24 Sistema de coordenadas de un aislador.
Interesa encontrar la matriz de rigidez del aislador en coordenadas globales, para ello
se debe determinar en primer lugar la matriz de paso , definida de la siguiente manera:
p
T
p
Esta matriz es:
T
0
1
0
0
1
0
0
1
1 lj
l
0 i
Sean 0
K y
0
K las matrices de rigidez asociadas a las coordenadas locales y globales
del aislador. Se conoce la matriz de rigidez 0
K y para encontrar
0
K se utiliza la siguiente
ecuación. Aguiar (2004).
T
K
T
K t
0
0
Una vez que se tiene la matriz de rigidez de cada aislador en coordenadas globales, se
encuentra la contribución de los aisladores a la matriz de rigidez de la estructura por
ensamblaje directo utilizando los vectores de colocación. Esto se lo hace con el programa
kaisladores, que se lista a continuación.
function [KELAS]=kaisladores(ngl,nais,Ko,Lo,VCAIS)
%
% Programa para encontrar la contribución de los aisladores a la
% Matriz de rigidez de un pórtico
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2009
%-------------------------------------------------------------
% [KELAS]=kaisladores(ngl,nais,Ko,Lo,VCAIS)
%-------------------------------------------------------------
(8.50)
( 8.51)
(8.49)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-326-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
316
% ngl Número de grados de libertad de la estructura
% nais Número de aisladores de la estructura
% Ko Matriz que contiene la rigidez horizontal y vertical de cada
% uno de los aisladores, colocados en la diagonal Ko(2*nais,2*nais)
% Lo Matriz de transformación de coord. locales a globales en aislador
% Tiene 2 filas y 6 columnas
% VCAIS Matriz que contiene los vectores de colocación de los aisladores
%
% KELAS Matriz que contiene la contribución de los aisladores a la matriz
% de rigidez de la estructura
%
KELAS=zeros(ngl);
for i=1:nais
ii=[1:2]+(i-1)*2;
K=Ko(ii,ii); % Rigidez en coordenadas locales
KG=Lo'*K*Lo; % Rigidez en coordenadas globales
for j=1:6
jj=VCAIS(i,j);
if jj==0
continue
end
for m=1:6
mm=VCAIS(i,m);
if mm==0
continue
end
KELAS(jj,mm)=KELAS(jj,mm)+KG(j,m);
end
end
end; return
%---fin---
Figura 8.25 Modelo de masas puntuales.
8.7.3 Matriz de Masas
Para encontrar la matriz de masas M se concentró la masa en los nudos, como se
observa en la figura 8.25. Los giros son muy bajos en comparación a los desplazamientos](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-327-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
317
laterales, por esto los giros son coordenadas secundarias pero como se está trabajando con
todos los grados de libertad se considera la energía cinética de rotación que vale
J siendo
J el momento de inercia de la masa que es igual a
2
r
m
J , donde r es el radio de giro que
se considera igual a 20
/
L
r .
El programa que determina la matriz de masas en el sistema CEINCI-LAB se
denomina: masas_ais.
function [M]=masas_ais(ngl,L,VC,Fm,g)
%
% Programa que calcula la Matriz de masas en pórticos planos
% con un modelo de masas puntuales
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2009
%-------------------------------------------------------------
% [M]=masas_ais(ngl,L,VC,Fm,g)
%-------------------------------------------------------------
% ngl número de grados de libertad
% L Vector que contiene la longitud de los elementos
% VC Matriz de vectores de colocación de elementos
% Fm Matriz con: Núm elem, Carga, Código, elem a gener, incr. num elem.
% Código=1 Carga Uniforme en elemento horizontal
% Código=2 Carga Triangular en elemento horizontal
% g aceleración de la gravedad
%
% M Matriz de masas
M=zeros(ngl);
nf=length(Fm(:,1)); % Número de filas de datos
for icon=1:nf
i=Fm(icon,1); % Numero de elemento cargado
P=Fm(icon,2); % Carga en elemento
icod=Fm(icon,3); % Código del tipo de carga
ielem=Fm(icon,4); % Elementos a generar con igual carga y longitud
icr=Fm(icon,5); % Incremento en la numeración de elementos con igual carga
if icod==1 % CARGA UNIFORME EN ELEMENTO
radio=L(i)/20;
m(1)=P*L(i)/(2*g);m(2)=m(1);m(3)=(P*L(i)/(2*g))*radio*radio;
m(4)=m(1);m(5)=m(1);m(6)=m(3);
end
for ij=1:6
gdl=VC(i,ij);
if gdl==0
continue
else
M(gdl,gdl)=M(gdl,gdl)+m(ij);
end
end
for ik=1:ielem
for ki=1:6
gdl=VC(i+ik*icr,ki);
if gdl==0
continue
else](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-328-320.jpg)

![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
319
Considerar que la rigidez vertical de los aisladores es 100 veces la rigidez horizontal.
Se pide encontrar la respuesta en el tiempo en los grados de libertad 1, 6 y 11 (ver figura 8.21)
ante la componente N-S., del sismo de El Centro de 1940. Presentar el desplazamiento relativo
del segundo piso, con respecto al primer piso.
Encontrar también el desplazamiento lateral máximo y para dicho valor encontrar las
fuerzas y momentos en cada uno de los elementos de hormigón armado.
SOLUCIÓN
El programa desarrollado para resolver el Ejemplo 7, utilizando la librería de programas
de CEINCI-LAB se indica a continuación.
clear all; close all; echo off
%
% Programa para el análisis sísmico de Pórtico con
% Aisladores Elástoméricos en la parte superior de las columnas
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Noviembre de 2009
%-------------------------------------------------------------
% aislador_elastomerico_ej1_libro
%-------------------------------------------------------------
% 1. Datos generales
L1=5.0; H=3.0; %Longitud y altura del pórtico
bv=0.40; hv=0.60; %base y altura de las vigas
bc=0.60; hc=0.60; %base y altura de columnas
bm=0.20; %ancho de mampostería
zeda=0.05; %Factor de amortiguamiento de superestructura
zedab=0.15; %Factor de amortiguamiento de aisladores
li=0.10;h=0.40;lj=0.10;% Dimensiones en altura de aislador
nais=2; %Número de aisladores
Tb=2.0; % Período objetivo de sistema de aislación
g=9.81; % Aceleración de la gravedad
E=1800000; % Modulo de elasticidad del material
njc=0; F=0; % Número de juntas cargadas. Se debe colocar F=0
%--------------------------------------------------------------------------
% 1. Cálculo de reacciones en superestructura
nod=4; % Número de nudos del pórtico de superestructura
gdlv=[2 4]; % grados de libertad verticales de aisladores
nmc=2; % Número de miembros cargados de superestructura
Fm=[1 3.0 1 0 0;%Elem carg, carga, código, elem a gener, incr numero elemento
4 2.0 1 0 0];%Carga uniforme repartida en viga 4.
CG=[1 2 3;1 4 5;6 7 8;6 9 10];
ngl=10; % Número de grados de libertad de superestructura
% MATRIZ DE GENERACION DE NUDOS DE LOS ELEMENTOS
GEN=[1 1 2 1 3 2 2; %elem, ni, nf, elem a gene, inc en elem, inc en ni, inc en nf
2 1 3 1 1 1 1];
% Generación de vector NI (Nudo Inicial) y NJ (Nudo Final) de elementos
[NI,NJ]=gn_portico(GEN);
% MATRIZ DE GENERACION DE COORDENADAS DE LOS NUDOS
NUDOS=[1 0.0 0.0 0 0 0 0;% i, xi, yi, nudos a gener, incr num nudo, dx,dy
2 L1 0.0 0 0 0 0;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-330-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
320
3 0.0 H 0 0 0 0;
4 L1 H 0 0 0 0];
% Generación de las coordenadas de los nudos
[X,Y]=glinea_portico(NUDOS);
% Dibuja la superestructura
dibujo (X,Y,NI,NJ);
% Vector de colocación
[VC]=vc(NI,NJ,CG);
% Longitud, Seno y Coseno de elementos
[Ls,senos,cosenos]=longitud (X,Y,NI,NJ);
% Secciones de los elementos
SECCION=[1 bv hv 1 3; % Eleme, base, altura, elem a gener, increm en elem
2 bc hc 1 1];
[ELEM]=gelem_portico(SECCION);
% Matriz de rigidez de la estructura
[K]=krigidez(ngl,ELEM,Ls,senos,cosenos,VC,E); %Matriz Rigidez Estructura
r=[1:ngl];r1=[1,2,3,4,5]; %Grados de libertad para calcular reacciones apoyos
r2=setdiff(r,r1); %Grados de libertad de nudos libres
Kaa=K(r1,r1);Kab=K(r1,r2);Kbb=K(r2,r2);
Xi=-KbbKab'; %Matriz de influencia estática
Kbf=Kbb; % Matriz de rigidez con base empotrada
% Cargas solo en los elementos horizontales
[Q,Q2]=cargas(njc,nmc,ngl,Ls,senos,cosenos,CG,VC,F,Fm);
% Kaa*qa+Kab*qb=F1+R; Kab'*qa+Kbb*qb=F2
F2=Q(r2);qb=KbbF2;
% Cálculo de las reacciones
F1=Q(r1);% Son las contribuciones de los elementos cargados
R=Kab*qb-F1;
%-----------------------------------------------------------------------
% 2. Rigidez de aisladores elastoméricos
wn=2*pi/Tb;% Frecuencia para Tb=2 s. wn=2*pi/T
Mo=R(gdlv)/g; % Masas de los apoyos con aisladores
Kb=diag([wn^2*Mo]);% Rigidez de los aisladores horizontales
for k=1:nais % Rigidez de aisladores en diagonal (kb, kv) de cada aislador
kk=[1:2]+(k-1)*2;
Ko(kk,kk)=[Kb(k,k) 0; 0 100*Kb(k,k)]; % Rigidez de aislador horiz. y vert.
end
%--------------------------------------------------------------------------
% 3. Matriz de rigidez, superestructura y subestructura
CG=[0 0 0;0 0 0;1 2 3;1 4 5;6 7 8;6 9 10;11 12 13;11 14 15];
ngl=15; % Número de grados de libertad de superestructura y subestructura
% MATRIZ DE GENERACION DE NUDOS DE LOS ELEMENTOS
GEN=[1 1 3 1 1 1 1; %elem, ni, nf, elem a gene, inc en elem, inc en ni, inc en nf
3 3 4 1 1 2 2;
5 5 7 1 1 1 1;
7 7 8 0 0 0 0;
8 3 5 1 1 1 1];
% Generación de vector NI (Nudo Inicial) y NJ (Nudo Final) de elementos
[NI,NJ]=gn_portico(GEN);
% MATRIZ DE GENERACION DE COORDENADAS DE LOS NUDOS
NOD=[1 0.0 0.0 0 0 0 0;% i, xi, yi, nudos a gener, incr num nudo, dx,dy
2 L1 0.0 0 0 0 0;
3 0.0 H 0 0 0 0;
4 L1 H 0 0 0 0;
5 0.0 H+h 0 0 0 0;
6 L1 H+h 0 0 0 0;
7 0.0 2*H+h 0 0 0 0;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-331-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
321
8 L1 2*H+h 0 0 0 0];
% Generación de las coordenadas de los nudos
[X,Y]=glinea_portico(NOD);
% Dibuja la superestructura
dibujo (X,Y,NI,NJ);
% Vector de colocación
[VC]=vc(NI,NJ,CG);
% Longitud, Seno y Coseno de elementos
[L,seno,coseno]=longitud (X,Y,NI,NJ);
% Secciones de los elementos solo vigas y columnas
SECC=[1 bc hc 1 1; % Eleme, base, altura, elem a gener, increm en elem
3 bv hv 1 1;
5 bc hc 1 1;
7 bv hv 0 0];
[ELEMEN]=gelem_portico(SECC);
% Matriz de rigidez de la estructura
[K]=krigidez(ngl,ELEMEN,L,seno,coseno,VC,E); %Matriz Rigidez Estructura sin aisladores
%--------------------------------------------------------------------------
%4. Contribución de aisladores
% Vector de colocación de aisladores
VCAIS=[1 2 3 6 7 8;
1 4 5 6 9 10];
Lo=[-1 0 -li 1 0 -lj;
0 -1 0 0 1 0];%[d1,d2]=Lo*[p(i);p(j)]
[KELAS]=kaisladores(ngl,nais,Ko,Lo,VCAIS);% KELAS es la contribución de los aisladores
KT=K+KELAS;% Mariz de rigidez estructura con aisladores
%--------------------------------------------------------------------------
%5. Matriz de masas y de amortiguamiento
% Matriz de Masas (Modelo de masas puntuales)
Fmasa=[3 0.576 1 0 0;%Elem carg, carga, código, elem a gener, incr numero elemento
4 3.0 1 0 0;
7 2.0 1 0 0];%Carga uniforme repartida en viga 4.
[M]=masas_ais(ngl,L,VC,Fmasa,g);
% Matriz de amortiguamiento
[T,phi,omega]=orden_eig(KT,M);% Períodos y Frecuencias de vibración
[C]=amortiguamiento(M,phi,omega,zeda);
Cb=diag(2*zedab*wn*Mo); % Amortiguamiento horizontal de los aisladores
for k=1:nais
kk=[1:2]+(k-1)*2;
Co(kk,kk)=[Cb(k,k) 0; 0 0]; % Amortiguador de aislador horiz
end
[CELAS]=Caisladores(ngl,nais,Co,Lo,VCAIS);% Contribución de aisladores
CC=C+CELAS;
%--------------------------------------------------------------------------
%6. Vectores de incidencia
S=zeros(ngl,2);Jh=zeros(ngl,1);
pp=CG(:,1); k1=pp(find(pp>0)); Jh(k1,1)=1; %Sismo horizontal
pp=CG(:,2); k2=pp(find(pp>0)); Jv(k2,1)=1; %Sismo vertical
% Respuesta en el tiempo ante componente horizontal
load rec_centro
nn=length(ux);tu(1)=0;ugx=0.01*ux; %Acelerograma viene en gals
% Condiciones iniciales
qp=zeros(ngl,1);q=qp; %Vector de velocidades y desplazamientos iniciales nulos
Y=[q;qp]; % El vector inicial de q es el de las cargas verticales estáticas.
Y1=Y; % Para segunda corrida en que se halla vector q asociado a desp. max. de aisl.
%qmax=zeros(ngl,1);% Para calcular desplazamientos máximos en diferentes tiempos
%qmax1=zeros(ngl,1);% Para calcular desplazamientos cuando se produce desplaz1 max](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-332-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
322
% Respuesta en el tiempo de aisladores punto en punto
for iji=1:nn-1
iji
acel=-ugx(iji);tu(iji+1)=iji*dT;
[Yn]=pee_de_uno(KT,CC,M,Jh,acel,dT,Y);
Y=Yn;
for i=1:ngl;
if i==1 % Se almacena desplazamiento inferior de aislador de base
q1t(1,iji+1)=Y(1);
end
if i==6 % Se almacena desplazamiento superior de aislador de base
q6t(1,iji+1)=Y(6);
end
if i==11 % Se almacena desplazamiento en segundo piso de estructura
q11t(1,iji+1)=Y(11);
end
end
end
for i=1:length(q1t)
q6tr(1,i)=q6t(1,i)-q1t(1,i); %desplazamientos relativos de 6 con 1
q11tr(1,i)=q11t(1,i)-q6t(1,i); %desplazamiento realtivo de 11 con 6
end
[qmaxaislador,ind]=max(q6t(1,:)) % ind es el instante de despla. máximo
Y=Y1; % Se inicia de nuevo en cero
for iji=1:ind % Vector q asociado a desplazamiento máximo aislador
iji
acel=-ugx(iji);
[Yn]=pee_de_uno(KT,CC,M,Jh,acel,dT,Y);
Y=Yn;
end
qmax=Y(1:ngl); % Desplazamientos y giros asociados a despl.- máx.
% Calculo de Momentos y Fuerzas máximas en los elementos en desp. max.
Q2=zeros(length(L),6);
[FF]=fuerzas(ngl,ELEMEN,L,seno,coseno,VC,E,qmax,Q2)% Por sismo en X
% Fuerzas en los aisladores
fprintf ('n Fuerzas y desplazamientos en los aisladores');
%[FFA,Dx]=fuerzas_aisladores(ngl,Ko,VCAIS,qmax,li,lj,h)% Por sismo
figure (1)
subplot(311), plot(tu',q1t');
subplot(312), plot(tu',q6t','r');
subplot(313), plot(tu',q11t','g')
figure (2)
subplot(111), plot(tu',q1t'); grid; hold on;
plot(tu',q6t','r:')
figure (3)
subplot(111);plot(tu',q6tr');
figure (4)
subplot(111);plot(tu',q11tr');
% ---end---
En la parte superior de la figura 8.26 se encuentra los desplazamientos laterales del
grado de libertad 1, bajo el aislador. Nótese que están multiplicados por , de tal manera
que prácticamente no se mueve la sub estructura.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-333-320.jpg)





![SISTEMAS DE UN GRADO DE LIBERTAD
328
La definición de espectro está relacionada a un sistema de un grado de libertad. Por lo
tanto el factor permite pasar la respuesta en desplazamientos, de un sistema de un
grado de libertad a un sistema de múltiples grados de libertad.
Se ha utilizado la definición de seudo espectro para encontrar el desplazamiento
espectral di
S .
di
i
ni
di
di A
T
W
A
S
2
2
2
Para tener la respuesta en las coordenadas se utiliza la ecuación (9.2) con lo que se
halla:
)
(
2
)
(
2
i
di
i
i
i
A
T
q
El factor de participación modal, se considera en valor absoluto y representa
que tanto participa el modo en la respuesta. Con la ecuación (9.11) se encuentra la respuesta
de una estructura en cada modo de vibración. Para hallar la respuesta total se debe utilizar un
criterio de combinación modal, que se estudiará en este capítulo, más adelante. Sin embargo
de ello a continuación se presenta el programa desplazamientos_modales de la librería de
CEINCI-LAB, que halla los desplazamientos máximos aplicando el Criterio de Combinación
modal de la Norma Técnica de Perú 2003. Se destaca que este criterio es bueno para edificios
pero no para Presas de Proyectos Hidroeléctricos. El usuario puede fácilmente modificar el
criterio, en el programa.
[qt]=desplazamientos_modales(T,phi,Ad,gama,na)
Datos:
T Periodos de vibración en cada modo de vibración de la estructura.
phi Matriz modal .
Ad Vector con las aceleraciones espectrales en cada modo de vibración.
gama Vector que contiene los factores de participación modal.
Na Número de modos con los que desea encontrar la respuesta sísmica.
Resultados:
qt Vector que contiene los desplazamientos elásticos máximos.
function [qt]=desplazamientos_modales(T,phi,Ad,gama,na)
%
% Programa que determina los desplazamientos en cada modo de vibración
% y los desplazamientos totales, aplicando el criterio de la Norma de Perú 2003
% Son desplazamientos totales Elásticos (sin multiplicar por el factor R)
%
% T Son los periodos de vibración en cada modo
% phi Es una matriz que contiene a los modos de vibración, primera columna
% es el primer modo de vibración, segunda columna es el segundo modo.
% Ad Es un vector que contiene las aceleraciones espectrales en cada
% modo de vibración.
% gama Es un vector con los factores de participación de cada modo
% na Número de modos de vibración
% q Es la matriz que contiene los desplazamientos en cada modo
% qt Es el vector de desplazamientos resultantes luego de la combinación modal
(9.11)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-339-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
330
sísmico plano, el vector contiene las fuerzas laterales en cada uno de los pisos, que se nota
también con la letra . Es solo nomenclatura. Aguiar (2004)
Nuevamente la ecuación (9.12) reporta las respuestas máximas de cargas (Fuerzas y/o
momentos) en cada modo de vibración. Para encontrar la resultante se debe aplicar un criterio
de combinación modal.
El programa del sistema de computación CEINCI-LAB que determina las fuerzas
resultantes se denomina fuerzas_modales y se presenta a continuación.
function [Ft]=fuerzas_modales(M,phi,Ad,gama,na)
%
% Programa que determina las fuerzas en cada modo de vibración
% y las fuerzas totales, aplicando el criterio de la Norma de Perú 2003
%
% M Es la matriz de masas
% phi Es una matriz que contiene a los modos de vibración, primera columna
% es el primer modo de vibración, segunda columna es el segundo modo.
% Ad Es un vector que contiene las aceleraciones espectrales en cada
% modo de vibración.
% gama Es un vector con los factores de participación de cada modo
% na Número de modos de vibración
% P Es la matriz que contiene las fuerzas en cada modo
% Ft Es el vector de fuerzas resultantes luego de la combinación modal
% Criterio 0.25 Valor Absoluto+0.75 Valor Máximo Probable
% --------------------------------------------------------------
% Dr. Roberto Aguiar
% Octubre de 2010
% CEINCI-ESPE
%---------------------------------------------------------------
masafi=M*phi; gamaAd=(gama.*Ad)';
for i=1:na
for j=1:na
P(j,i)=gamaAd(i)*masafi(j,i);
end
end
for i=1:na % Criterio de Combinación Modal de Norma Técnica de Perú 2003
RRR(i)=0; RR(i)=0;
for j=1:na
RRR(i)=RRR(i)+abs(P(i,j));RR(i)=RR(i)+P(i,j)*P(i,j);
end
Ft(i)=0.25*RRR(i)+0.75*sqrt(RR(i));
end; return
9.4 CRITERIOS DE COMBINACIÓN MODAL
En el Método de Superposición Modal, se hallan las respuestas en cada modo de
vibración y para encontrar la respuesta resultante, se debe aplicar un criterio de combinación
modal. En la literatura existen una gran cantidad de criterios entre los que se destacan los
siguientes:
Criterio del Máximo Valor Probable (SRSS)
Sea r un cierto valor de respuesta que se desea obtener, puede ser un
desplazamiento, un momento, un corte, etc. El criterio del valor máximo probable, es:](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-341-320.jpg)








![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
339
las dimensiones de los elementos estructurales debido a que con esa deriva se espera un gran
daño en la estructura. Ghobarath et al. (1997).
Efecto
Cuando se tienen desplazamientos laterales significativos, el peso propio tiende a
voltearla, de tal manera que en la estructura deformada, por la acción sísmica, actúan cargas
adicionales los mismos que son tomados en cuenta cuando se analiza con teoría de segundo
orden. Las normativas sísmicas tratan este tema en forma simplificada controlando el efecto
. Para ello se debe determinar el índice de estabilidad de piso .
i
i
ei
i
i
h
V
P
Donde es la carga vertical que gravita desde el piso i hasta el tope, se calcula en
función de la carga muerta D más el porcentaje de la carga viva L; es el cortante de piso;
es la deriva de piso calculada con los desplazamientos elásticos , y es la altura de
entrepiso. Se destaca que es la deriva de piso elástica.
El NEC-11 establece que si la estructura no tiene problemas de efecto
P y se prosigue con el cálculo pero si la estructura debe ser reforzada a menos
que se demuestre mediante un análisis de segundo orden que la estructura sigue siendo
estable. Finalmente si tanto las derivas de piso como las fuerzas estáticas se
multiplicarán por.
i
P
f
1
1
Con relación a la estructura de dos pisos que se está analizando en la tabla 9.2 se
presenta el control del efecto . .
Tabla 9.2 Cálculo del índice de estabilidad de piso.
Piso Fuerza
Horizontal
( T. )
Cortante
( T. )
Peso desde
piso al tope
( T. )
Deriva de
piso elástica
i
1 1.41 4.72 19.80 0.0046 0.0190
2 3.31 3.31 9.9 0.0060 0.0178
Programa modal_plano_nec
function [V]=modal_plano_nec(alt,pesoD,pesoL,KL)
%
% Análisis Modal plano de acuerdo al NEC-11
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Abril de 2012
%-----------------------------------------------------------------------
% [V]=modalplanonew(alt,pesoD,pesoL,KL,KLG)
%-----------------------------------------------------------------------
% alt Vector que contiene las alturas a cada piso medido desde la base.
% pesoD Vector que contiene la carga muerta D de cada piso.
% pesoL Vector que contiene el porcentaje de carga viva L de cada piso.
% KL Matriz de rigidez lateral del pórtico con inercias agrietadas.
%-----------------------------------------------------------------------
(9.26)
(9.27)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-350-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
340
% PESO Peso total Reactivo calculado con carga viva V Cortante Basal
% H Altura total del edificio
%-----------------------------------------------------------------------
NP=length(alt);H=alt(NP); for i=1:NP-1; j=NP-i+1; alt(j)=alt(j)-alt(j-1);end
%Matriz de masas
for i=1:NP; masaD(i)=pesoD(i)/9.8; masaL(i)=pesoL(i)/9.8;
mas(i)=masaD(i)+masaL(i);end
masa=zeros(NP,NP);for i=1:NP; masa(i,i)=mas(i);end
PESO=0;for i=1:NP; PESO=PESO+pesoD(i)+pesoL(i);end;
% Periodos de vibración y periodo fundamental
[T,fi,OM]=orden_eig(KL,masa);Tf=T(1);
R=4;fip=1;fie=1; % Reducción de espectro elástico a inelástico
% Aceleraciones modales
[Ad]=espectro_nec11 (R,fip,fie,T);
I=1; % Factor de Importancia
Ad=I*Ad; % Ad ya está dividida para el factor R.
%Cortante basal Mínimo
Sa=Ad(1)/9.8;Vmin=I*Sa*PESO
%Factores de participación modal
for i=1:NP; b(i)=1; end;b=b';NUM=fi'*masa*b;DEN=diag(fi'*masa*fi);
for i=1:NP; gama(i)=abs(NUM(i)/DEN(i));end
%Fuerzas modales
masafi=masa*fi;gamaAd=(gama.*Ad)';
for i=1:NP;
for j=1:NP;
P(j,i)=gamaAd(i)*masafi(j,i);
end
end
%Cortantes
VV=zeros(NP,NP);
for i=1:NP;
for j=1:NP;k=NP+1-j;
if k==NP;
VV(k,i)=VV(k,i)+P(k,i);
else
VV(k,i)=VV(k+1,i)+P(k,i);
end
end
end
%Criterio de Norma Técnica de Perú de 2003 se aplica en cortantes
for i=1:NP
RRR(i)=0; RR(i)=0;
for j=1:NP
RRR(i)=RRR(i)+abs(VV(i,j)); RR(i)=RR(i)+VV(i,j)*VV(i,j);
end
Corte(i)=0.25*RRR(i)+0.75*sqrt(RR(i));
end;Corte=Corte';
% Cálculo de las Fuerzas Laterales
for i=1:NP
j=NP+1-i;
if j==NP
F(j)=Corte(j);
else
F(j)=Corte(j)-Corte(j+1);
end
end
%Control del Cortante Basal Mínimo](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-351-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
341
V=sum(F);F=F';
if Vmin > V; factor1=Vmin/V; F1=factor1*F; else F1=F; end;
%Control de la deriva de los pórticos
q=KLF1;qine=0.75*R*q; F=F';
for i=1:NP
j=NP+1-i;
if j==1
drift(j)=qine(j)/alt(j);drife(j)=q(j)/alt(j);
else
drift(j)=(qine(j)-qine(j-1))/alt(j);
drife(j)=(q(j)-q(j-1))/alt(j);
end
end
gamamax=max(drift)*100;
fprintf ('n Modos de vibracion');fi
fprintf ('n Periodos de vibracion');T
fprintf ('n Factores de participacion');gama
fprintf ('n Aceleraciones espectrales');Ad
fprintf ('n Cortante Basal Minimo ');Vmin
fprintf ('n Fuerzas laterales en los porticos sin controles');F=F'
fprintf ('n Desplazamientos laterales inelasticos');qine
fprintf ('n Derivas de piso'); drift=drift'
fprintf ('n Deriva maxima de piso en porcentaje, sin control de P-Delta');gamamax
%Control de efecto P-Delta
for i=1:NP
j=NP-i+1;
if j==NP
Peso(j)=masa(j,j)*9.8;Corte(j)=F1(j);
else
Peso(j)=masa(j,j)*9.8+Peso(j+1);Corte(j)=F1(j)+F1(j+1);
end
theta(j)=(Peso(j)/Corte(j))*drife(j);
if theta(j)>=0.30
fprintf ('n Estructura debe ser reforzada');
elseif theta(j)>=0.10 & theta(j)<0.30
fpd(j)=1/(1-theta(j));
else
fpd(j)=1;
end
end
F2=max(fpd)*F1;V=sum(F);gamamax=max(fpd)*gamamax;
fprintf ('n Deriva maxima de piso en porcentaje, con control de P-Delta');gamamax
fprintf ('n Indice de estabilidad de piso');theta'
fprintf ('n Fuerzas laterales finales luego de controles');F2
%---fin
Programa espectro_nec11
function [Ad]=espectro_nec11 (R,fip,fie,T)
% Programa que determina las aceleraciones espectrales para determinados
% períodos de vibración. Utilizando la nueva Normativa Ecuatoriana de la
% construcción NEC-11. Versión Octubre de 2011
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
% Abril de 2012
%----------------------------------------------------------------------](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-352-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
342
% [Ad]=espectro_nec11 (R,fip,fie,T)
%-----------------------------------------------------------------------
% R Factor de reducción de las fuerzas sísmicas
% fip Factor de irregularidades en planta
% fie Factor de irregularidades en elevación
% T Períodos de vibración
% Resultados:
% Ad Aceleraciones Espectrales para cada período de vibración en m/seg2
%-----------------------------------------------------------------------
% Sae Espectro Elástico
% Fa Factor de amplificación de las ordenadas espectrales por efecto
% del tipo de suelo.
% Fd Factor de amplificación de las ordenadas espectrales por efecto
% del tipo de suelo.
% Fs Factores que toma en cuenta comportamiento no lineal del suelo, la
% degradación del período y desplazamientos relativos del suelo.
np=length(T); %Número de puntos para determinar aceleraciones espectrales
FAC=R*fip*fie;
is=input ('n Ingrese código para perfil de suelo 1=A, 2=B, 3=C, 4=D, 5=E :');
iz=input ('n Ingrese zona sísmica 1=0.15 g, 2=0.25 g, 3=0.30 g, 4=0.35, 5=0.4 g, 6=0.5 g :');
ip=input ('n Ingrese código de Región 1=Costa, 2=Sierra, 3=Oriente :');
FA=[0.9 0.9 0.9 0.9 0.9 0.9;
1 1 1 1 1 1;
1.4 1.3 1.25 1.23 1.2 1.18;
1.6 1.4 1.3 1.25 1.2 1.15;
1.8 1.5 1.4 1.28 1.15 1.05];
FD=[0.9 0.9 0.9 0.9 0.9 0.9;
1 1 1 1 1 1;
1.6 1.5 1.4 1.35 1.3 1.25;
1.9 1.7 1.6 1.5 1.4 1.3;
2.1 1.75 1.7 1.65 1.6 1.5];
FS=[0.75 0.75 0.75 0.75 0.75 0.75;
0.75 0.75 0.75 0.75 0.75 0.75;
1.0 1.1 1.2 1.25 1.3 1.45;
1.2 1.25 1.3 1.4 1.5 1.65;
1.5 1.6 1.7 1.8 1.9 2.0];
Fa=FA(is,iz);Fd=FD(is,iz);Fs=FS(is,iz);
if iz==1; z=0.15; end; if iz==2; z=0.2; end; if iz==3; z=0.3; end
if iz==4;z=0.35; end; if iz==5;z=0.4; end; if iz==6;z=0.45; end
To=0.1*Fs*Fd/Fa; % Período To
Tc=0.55*Fs*Fd/Fa; % Período donde inicia rama descendente de espectro
if is==1; r=1; end; if is==2; r=1; end; if is==3; r=1; end;
if is==4; r=1.5; end; if is==5; r=1.5; end;
if ip==1; eta=1.8; end; if ip==2; eta=2.48; end; if ip==3; eta=2.6; end
for i=1:np
if T(i) <= To
Sa(i)=z*Fa*(1+(eta-1)*(T(i)/To))*9.8;Ad(i)=Sa(i)/FAC;
end
if T(i) > To & T(i) <= Tc
Sa(i)=eta*z*Fa*9.8;Ad(i)=Sa(i)/FAC;
end
if T(i) > Tc
Sa(i)=eta*z*Fa*9.8*(Tc/T(i))^r;Ad(i)=Sa(i)/FAC;
end
end
return](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-353-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
344
Las matrices de rigidez lateral de los pórticos indicados en la figura 9.7, encontradas
con inercias agrietadas, para un módulo de Elasticidad , que se encontró
con el programa rlaxinfi, son las siguientes:
* +
* +
Figura 9.7 Pórtico tipo en sentido X, y en sentido Y.
SOLUCIÓN
La matriz de Masas, para las coordenadas de piso indicada en la figura 9.8, es:
[ ]
Figura 9.8 Coordenadas de piso en el Centro de Masa.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-355-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
345
% Análisis Espacial en Coordenadas de Piso, utilizando Espectro
% del NEC-11 y empleando Método de Superposición Modal
%
% Dr. Roberto Aguiar
% Abril de 2012
%--------------------------------------------------------------
% 1.- Matrices de rigidez lateral
K1=[4331.2 -1642.2;-1642.2 978.6];
KA=[2721.7 -1124.9;-1124.9 784.1];
% 2.- Matriz de rigidez en coordenadas de piso
ntot=6;iejes=3;NP=2;
r=[-3;0;3;-4;0;4];KL=[K1;K1;K1;KA;KA;KA];RT=r;
[KE,rtet,A]=matriz_es(ntot,iejes,NP,r,KL,RT);
% 3.- Matriz de masas
m=3.1837;J=26.5306;
M=[m 0 0 0 0 0;0 m 0 0 0 0;0 0 m 0 0 0;0 0 0 m 0 0;
0 0 0 0 J 0; 0 0 0 0 0 J];
% 4.- Propiedades Dinámicas
[T,fi,OM]=orden_eig(KE,M);
% 5.- Aceleraciones Espectrales
R=4;fip=1;fie=1;
[Ad]=espectro_nec11 (R,fip,fie,T);
% 6.- Factores de participación modal para sismo en X
b=[1;1;0;0;0;0];
NUM=fi'*M*b;DEN=diag(fi'*M*fi);
for i=1:6; gama(i)=abs(NUM(i)/DEN(i));end
% 7.- Desplazamientos Modales
na=6;
[q]=desplazamientos_modales(T,fi,Ad,gama,na)
qine=R*q
% 8.- Fuerzas Modales
[Ft]=fuerzas_modales(M,fi,Ad,gama,na)
En la tabla 9.3 se indican los períodos de vibración (con inercias agrietadas) y los
factores de participación modal.
Tabla 9.3 Períodos de vibración y factores de participación modal.
Modo 1 2 3 4 5 6
0.395 0.369 0.271 0.114 0.092 0.074
0 2.326 0 0 0.978 0
La estructura analizada no tiene problemas de torsión, por esta razón cuando actúa el
sismo en sentido X, los desplazamientos laterales solo existen en ese sentido y no hay giros de
torsión; en la tabla 9.4 se presentan estos desplazamientos y fuerzas estáticas equivalentes en
coordenadas de piso, en la figura 9.9 se indican estas fuerzas estáticas que deben ser
repartidas a los pórticos.
Tabla 9.4 Desplazamientos y Fuerzas en Sentido X, en coordenadas de piso.
Piso 1 2
Desplazamiento Elástico
Horizontal (cm)
0.5 1.21
Desplazamiento Inelástico
Horizontal (cm.)
2.0 4.86
Fuerza lateral en sentido X
(T.)
6.25 11.61](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-356-320.jpg)


![SISTEMAS DE UN GRADO DE LIBERTAD
348
armado de un piso tipo y de sección idéntica a la del aislador; también presenta ecuaciones
para hallar la rigidez vertical del aislador para producir una frecuencia vertical de vibración
superior a 10 Hz.
La matrices de rigidez y de masas, relacionadas con las coordenadas laterales 1 y 2,
son las siguientes:
* + * +
Los períodos de vibración que se hallan con estas matrices, son:
[ ]
Se recuerda que el período objetivo de la estructura es 2.0 seg. Por este motivo se
obtuvo ese período en el primer modo. Los modos de vibración son:
* + * +
El espectro del NEC-11 es para un factor de amortiguamiento del 5%. Ahora la
estructura va a tener aisladores de base que tienen un factor de amortiguamiento de 15%.
Habría que encontrar el factor de amortiguamiento de todo el sistema, hay varios trabajos al
respecto uno de ellos es el propuesto por Inaudi et al. (1993) denominado “Energía Modal de
Deformación”, en el que se determina el factor de amortiguamiento en función de las
propiedades dinámicas (frecuencia natural de vibración) de la estructura sin y con aisladores de
base y de los factores de amortiguamiento.
En el presente ejercicio se considera que el factor de amortiguamiento equivalente es
igual al factor de amortiguamiento que tiene la estructura (5%) más el factor de
amortiguamiento de los aisladores (15%) con lo que se obtiene un . Para encontrar el
espectro asociado a este amortiguamiento a partir del espectro del NEC-11, se encuentra el
factor con el que se debe multiplicar las ordenadas espectrales con la siguiente ecuación.
( )
El UBC (1997) propone en forma conservadora determinar el factor de reducción por
amortiguamiento que es el inverso de , mediante la tabla 9.5, en función del
amortiguamiento efectivo del sistema de aislación,
Tabla 9.5 Factores de modificación de respuesta por amortiguamiento.
5 10 20 30 40
0.8 1.0 1.2 1.5 1.7 1.9 2.0
Luego el espectro elástico para 5% de amortiguamiento, habrá que dividir para el valor
, se destaca que es bastante conservador esta propuesta. La Norma Chilena de Aislación
Sísmica presenta una propuesta para calcular para los tres perfiles de suelo de su código.
Los desplazamientos laterales que se encuentran son:
* +
Nótese que el aislador es el que se desplaza 22.68 cm.; en la parte inferior del aislador
el desplazamiento lateral esperado es 0.03 cm.
(9.28)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-359-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
349
Las fuerzas estáticas equivalentes en los grados de libertad 1 y 2, son:
* +
El programa que se elaboró para resolver este ejercicio es el siguiente:
% Programa para el Análisis Sísmico Plano de un Pórtico Plano
% con Aisladores de Base Elastoméricos ubicados sobre las columnas
% del Primer Piso
%
% Dr. Roberto Aguiar
% 4 de Abril de 2012
%-------------------------------------------------------------
% 1.- Rigidez de aisladores
kb= 9.064;kv=10*kb;
ko=[kb 0; 0 kv];
% 2.- Geometría y Grados de libertad de Pórtico
nod=6;np=2;nr=2;mbr=6;nais=2;na=2;zedab=0.15;zeda=0.05;
[CG,ngl]=cg_aislador_col(nod,np,nr); % Arreglo CG
GEN=[1 1 3 1 1 1 1;
3 3 4 1 1 2 2;
5 3 5 1 1 1 1];
[NI,NJ]=gn_portico(GEN);
[VC]=vc(NI,NJ,CG);
X=[0.0; 6.0; 0.0; 6.0; 0.0; 6.0];
Y=[0.0; 0.0; 3.25; 3.25; 3.55; 3.55];
[L,seno,coseno]=longitud (X,Y,NI,NJ);
%dibujo(X,Y,NI,NJ);
% 3.- Contribución del Hormigón a la matriz de rigidez
LH=L(1:mbr-nais);
senH=seno(1:mbr-nais);cosH=coseno(1:mbr-nais);
VCH=VC(1:mbr-nais,1:6);
bc=0.3;hc=0.65; %dimensiones de las columnas
bv=0.20;hv=0.30; %dimensiones de las vigas
ELEMH=[bc hc;bc hc;bv hv;bv hv]; EH=1800000;
[SH]=krigidez(ngl,ELEMH,LH,senH,cosH,VCH,EH);
% 4.- Contribucion de los Aisladores
cero=zeros(2);li=0.05;lj=0.05;
Ko=[ko cero;
cero ko];
Lo=[-1 0 -li 1 0 -lj; % Matriz de Paso
0 -1 0 0 1 0];
VCAIS=VC(mbr-nais+1:mbr,1:6);
[SA]=kaisladores(ngl,nais,Ko,Lo,VCAIS);
%5.- Matriz de rigidez total
ST=SH+SA
%6.- Condensación Estática
Kaa=ST(1:na,1:na);Kab=ST(1:na,na+1:ngl);Kba=Kab';
Kbb=ST(na+1:ngl,na+1:ngl);K=Kaa+Kab*inv(Kbb)*Kba
%7.- Matriz de Masas
g=9.8;m1=0.5*6/g;m2=3*6/g;
M=[m1 0;0 m2];
% 8.- Propiedades Dinámicas
[T,fi,OM]=orden_eig(K,M);
% 9.- Ordenadas espectrales
R=1;fip=1;fie=1;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-360-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
350
[Ad]=espectro_nec11 (R,fip,fie,T);
% 10.- Factor de amortiguamiento del aislador
fa=(0.05/(zedab+zeda))^0.4;Ad=fa*Ad;
% 11.- Factores de Participación Modal
b=[1;1];NUM=fi'*M*b;DEN=diag(fi'*M*fi);
for i=1:na; gama(i)=abs(NUM(i)/DEN(i));end
gama
% 12.- Desplazamientos Modales
[q]=desplazamientos_modales(T,fi,Ad,gama,na)
% 13.- Fuerzas Modales
[Ft]=fuerzas_modales(M,fi,Ad,gama,na)
Se recomienda al lector si alguna subrutina que llama el programa, no la tiene que
intenté hacerlo con las otras subrutinas que se han indicado en este libro, de esta manera
afianzará sus conceptos.
REFERENCIAS
1. ACHISINA, (2001), Proposición de código para el análisis y diseño de edificios con
aislación sísmica, Asociación Chilena de Sismología e Ingeniería Sísmica, Grupo de
Protección Sísmica, Santiago de Chile.
2. Aguiar R., (2004), Análisis Matricial de Estructuras, Centro de Investigaciones
Científicas. Escuela Politécnica del Ejército. Tercera Edición, 550 p., Quito.
3. Chopra A., (2001), Dynamic of Structures: Theory and aplications to earthquake
engineering, 2
nd
edn., Prentice Hall: Saddle River New York.
4. Ghobarah A., Aly N. and El-Attar M. (1997) “Performance level criteria and evaluation.
A critical review of proposed guidelines”. Seismic design methodology for the next
generation of codes. Fajfar and Krawinkler Editors, Balkema, Slovenia.
5. Gómez J., (2002), “Presentación de un nuevo modelo matemático para cálculo de la
respuesta modal total de estructuras de edificios”, XIII Congreso Nacional de Ingeniería
Estructural, Colegio de Ingenieros Civiles de Puebla, 10 p., Puebla, México.
6. Iberisa (2008), “Puente solicitado por un espectro sísmico”, www.iberisa.com.
7. ICBO, (1997), Division IV-Earthquake Regulations for Seismic Isolated Structures,
Chapter 16, Uniform Building Code, 1997 Edition, International Conference of Building
Officials, Whittier, California
8. Inaudi J., Zambrano A., and Kelly J., (1993), On the analysis of structures with
viscoelastic dampers, Earthaquake Engineering Research Center, UBC/EERC-93/06,
119 p.
9. Norma E.030, (2003), Reglamento Nacional de Construcciones. Norma Técnica de
Edificaciones. Diseño Sismo resistente, Servicio Nacional de Normalización,
Capacitación e Investigación para la Industria de la Construcción. SENCICO, 36 p.,
Quito.
10. NRCC., (1990, National Building Code of Canada, Associate Committee on the National
Building Code. National Research Council of Canada, Ottawa.
11. Romo M., y Mosquera P., (2010), Puente sobre el estuario del río Chone, Primer
Encuentro Académico: “Puentes Siglo XXI”, Escuela Politécnica del Ejército, Noviembre
de 2010, Bahía de Caráquez.
12. Santana G., (2008), “Evaluación del Código Sísmico de Guatemala”,www.disaster-
info.net, 13 p.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-361-320.jpg)






![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
357
El programa vlibrevoladizo encuentra en forma gráfica los tres primeros modos de
vibración de una viga de sección constante en voladizo. La forma de uso del programa, es:
[v]=vlibrevoladizo(L)
L es la longitud de la viga en voladizo.
v es la forma modal.
function [V]=vlibrevoladizo(L)
%
% Vibraciones libres en un sistema continuo de una viga de flexion en voladizo
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [v]=vlibrevoladizo(L)
%-------------------------------------------------------------
% L : Longitud del elemento
% Las tres primeras raices de: 1+cos(p)*cosh(p)=0
% son: p1=1.875 p2=4.694 p3=7.854
% p=aL
% Constantes de Integracion
p1=1.875;a1=p1/L;dx=L/100; p2=4.694; a2=p2/L; p3=7.854; a3=p3/L;
A=1; C=-1; D1=(cos(p1)+cosh(p1))/(sinh(p1)-sin(p1));B1=-D1;
D2=(cos(p2)+cosh(p2))/(sinh(p2)-sin(p2));B2=-D2;
D3=(cos(p3)+cosh(p3))/(sinh(p3)-sin(p3));B3=-D3;
for i=1:100
x(i)=i*dx;
v1(i)=A*sin(x(i)*a1)+B1*cos(x(i)*a1)+C*sinh(x(i)*a1)+D1*cosh(x(i)*a1);
v2(i)=A*sin(x(i)*a2)+B2*cos(x(i)*a2)+C*sinh(x(i)*a2)+D2*cosh(x(i)*a2);
v3(i)=A*sin(x(i)*a3)+B3*cos(x(i)*a3)+C*sinh(x(i)*a3)+D3*cosh(x(i)*a3);
end
hold off
plot(v1,x,'--'); hold on
plot(v2,x,':'); plot(v3,x,'-.')
ylabel('Altura'); title('Formas modales de una viga en voladizo')
hold off
%---fin---
En la figura 10.4, se indican las tres primeras formas modales de la viga en voladizo del
ejemplo 1.
10.2.2 Viga apoyada
EJEMPLO 2
Encontrar los modos de vibración de la viga apoyada-apoyada, de sección constante,
presentada en la figura 10.5, calculada como un sistema continuo. Si la longitud es de 4.0 m.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-368-320.jpg)


![SISTEMAS DE UN GRADO DE LIBERTAD
360
En la figura 10.6 se indican las tres primeras formas modales de la viga apoyada-
apoyada.
El programa que encuentra los modos de vibración de una viga de sección constante,
apoyada-apoyada, se denomina vlibreapoyado y la forma de uso es la siguiente:
[v]=vlibreapoyado (L)
L es la longitud de la viga en voladizo.
v es la forma modal.
function [V]=vlibreapoyado(L)
%
% Vibraciones libres en un sistema continuo de una viga en voladizo
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [v]=vlibreapoyado(L)
%-------------------------------------------------------------
% L : Longitud del elemento
% Las cuatro primeras raices de: sen(p)*senh(p)=0
% son: p1=3.1416 p2=6.2832 p3=9,4248 p4=12.5664
% p=aL
% Constantes de Integracion
p1=pi;a1=p1/L;dx=L/100; p2=2*pi; a2=p2/L; p3=3*pi; a3=p3/L; p4=4*pi; a4=p4/L;
B=0; D=0; A=1; C1=-sin(p1)/sinh(p1); C2=-sin(p2)/sinh(p2);
C3=-sin(p3)/sinh(p3);
for i=1:100
x(i)=i*dx;
v1(i)=A*sin(x(i)*a1)+B*cos(x(i)*a1)+C1*sinh(x(i)*a1)+D*cosh(x(i)*a1);
v2(i)=A*sin(x(i)*a2)+B*cos(x(i)*a2)+C2*sinh(x(i)*a2)+D*cosh(x(i)*a2);
v3(i)=A*sin(x(i)*a3)+B*cos(x(i)*a3)+C3*sinh(x(i)*a3)+D*cosh(x(i)*a3);
end
hold off
plot(x,v1,'--'); hold on
plot(x,v2,':'); plot(x,v3,'-.');
xlabel('Longitud'); title('Formas modales de una viga apoyada-apoyada')
hold off
%---fin---
10.2.3 Interacción suelo estructura
En la figura 10.7 se indica el modelo que se considera la para el estudio de la
interacción suelo-estructura. Se tiene la viga a flexión de sección constante, con masa uniforme
distribuida, la misma que está simplemente apoyada y en su base existen dos resortes: un
horizontal de rigidez lineal d
k y uno rotacional de rigidez r
k .
Para el modelo numérico de las figura 10.7, las condiciones de borde, son:
i. En )
0
(
0 v
K
V
x d
ii. En )
0
(
0
r
k
M
x
iii. En 0
V
L
x
iv. En 0
M
L
x](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-371-320.jpg)


![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
363
De tal manera que el parámetro p conduce al cálculo de la frecuencia natural de
vibración.
Para resolver el ejercicio se elaboró el programa vlibreinteraccion cuya forma de
utilización es la siguiente:
[p] = vlibreinteraccion
function [p]=vlibreinteraccion
%
% Vibraciones libres en un sistema continuo de una viga en voladizo
% considerando la interaccion suelo estructura.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [p]=vlibreinteraccion
%-------------------------------------------------------------
% L : Longitud del elemento
% ii = kr/(EI/L) jj = kd/(EI/L3)
% kr : Rigidez rotacional del conjunto suelo-cimentacion
% kd : Rigidez traslacional del conjunto suelo-cimentacion
% p=aL
% Constantes de Integracion
tol=0.1; valores=[0.5; 5; 50; 500];
for k=1:4
ii=valores(k);
for jj=1:500
dx=0.001; icod=0;
for i=1:3000
p=i*dx; f1= p*((p*p/jj)+(1/ii))*sin(p)*cosh(p);
f2= p*((1/ii)-(p*p/jj))*cos(p)*sinh(p);
f3=(1-(p^4/(ii*jj)))*cos(p)*cosh(p);
f4=1+(p^4/(ii*jj));
ft=abs(f1-f2-f3-f4);
if ft <= tol & icod==0
pp(jj)=p; icod=1;
end
end
end
if k==1
p1=pp';
elseif k==2
p2=pp';
elseif k==3
p3=pp';
else
p4=pp';
end
end
hold off
plot(p1,'--'); hold on; plot(p2,':'); plot(p3,'-.'); plot(p4)
xlabel('Valores de j'); ylabel('Valores de p'), title('Primer modo')
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-374-320.jpg)







![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
371
Tabla 10.1 Masas modales de viga en flexión en voladizo
Modo j
__
*
m
mj
5
1
*
__
1
j
j
m
m
1 0.6130 0.6130
2 0.1882 0.8012
3 0.0648 0.8660
4 0.0315 0.8975
5 0.0391 0.9366
Las normativas sísmicas establecen que el mínimo número de modos de vibración que
se consideren en el cálculo sea tal que la suma de las masas modales sea mayor a 0.9, de tal
manera que con los resultados encontrados se debe trabajar con 5 modos de vibración.
La forma de uso del programa, es:
>> L=4
>> [m]= masamodalflexion (L)
function [m]=masamodalflexion (L)
%
% Calculo de masas modales de viga en flexion en voladizo.
% Calculo para los cinco primeros modos de vibracion
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [m]=masamodalflexion(L)
%-------------------------------------------------------------
% L : Longitud del elemento
% Las cinco primeras raices de: 1+cos(p)+cosh(p)=0
% son: p1=1.875 p2=4.694 p3=7.854 p4=10.996 p5=14.137
% p=aL
% Constantes de Integracion
p1=1.875;a1=p1/L;dx=L/100; p2=4.694; a2=p2/L; p3=7.854; a3=p3/L;
p4=10.996; a4=p4/L; p5=14.137; a5=p5/L;
A=1; C=-1; D1=(cos(p1)+cosh(p1))/(sinh(p1)-sin(p1));B1=-D1;
D2=(cos(p2)+cosh(p2))/(sinh(p2)-sin(p2));B2=-D2;
D3=(cos(p3)+cosh(p3))/(sinh(p3)-sin(p3));B3=-D3;
D4=(cos(p4)+cosh(p4))/(sinh(p4)-sin(p4));B4=-D4;
D5=(cos(p5)+cosh(p5))/(sinh(p5)-sin(p5));B5=-D5;
for i=1:100
x(i)=i*dx;
v1(i)=A*sin(x(i)*a1)+B1*cos(x(i)*a1)+C*sinh(x(i)*a1)+D1*cosh(x(i)*a1);
v2(i)=A*sin(x(i)*a2)+B2*cos(x(i)*a2)+C*sinh(x(i)*a2)+D2*cosh(x(i)*a2);
v3(i)=A*sin(x(i)*a3)+B3*cos(x(i)*a3)+C*sinh(x(i)*a3)+D3*cosh(x(i)*a3);
v4(i)=A*sin(x(i)*a4)+B4*cos(x(i)*a4)+C*sinh(x(i)*a4)+D4*cosh(x(i)*a4);
v5(i)=A*sin(x(i)*a5)+B5*cos(x(i)*a5)+C*sinh(x(i)*a5)+D5*cosh(x(i)*a5);
v11(i)=v1(i)*v1(i); v22(i)=v2(i)*v2(i); v33(i)=v3(i)*v3(i);
v44(i)=v4(i)*v4(i); v55(i)=v5(i)*v5(i);
end
NUM1=trapz(x,v1);NUM2=trapz(x,v2);NUM3=trapz(x,v3);
NUM4=trapz(x,v4);NUM5=trapz(x,v5)
DEN1=trapz(x,v11);DEN2=trapz(x,v22);DEN3=trapz(x,v33);
DEN4=trapz(x,v44);DEN5=trapz(x,v55);
m1=NUM1*NUM1/DEN1;m2=NUM2*NUM2/DEN2;m3=NUM3*NUM3/DEN3;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-382-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
372
m4=NUM4*NUM4/DEN4;m5=NUM5*NUM5/DEN5;
m=[m1/L; m2/L; m3/L; m4/L; m5/L]; suma=sum(m)
%---fin---
10.4.2 Respuesta en el tiempo
Para hallar la respuesta en el tiempo de una viga de flexión en voladizo ante una
acción sísmica se debe desarrollar un poco más la ecuación (10.44) que se copia a
continuación.
t
nj
L
j
nj
j
j d
t
W
sen
a
dx
x
m
W
m
t
y
0
0
__
*
)
(
)
(
)
(
La integral que contiene a la aceleración del tiempo es la que se desarrolla a
continuación:
t t
nj
nj
nj d
t
W
sen
t
senW
a
d
t
W
sen
a
0 0
cos
cos
)
(
)
(
t t t
nj
nj
nj d
sen
a
t
W
d
a
t
senW
d
t
W
sen
a
0 0 0
)
(
cos
cos
)
(
)
(
De tal manera que la ecuación (10.44) queda:
t t
nj
nj
L
j
nj
j
j d
sen
a
t
W
d
a
t
senW
dx
x
m
W
m
t
y
0 0
0
__
*
)
(
cos
cos
)
(
)
(
)
(
Para calcular las frecuencias naturales de vibración se trabaja con la ecuación (10.11)
en la que se sustituye L
p
a /
__
2
2
4
4
__
4
__
2
m
EI
L
p
W
L
p
m
EI
a
m
EI
W n
n
Al reemplazar:
137
.
14
996
.
10
854
.
7
694
.
4
875
.
1 5
4
3
2
1
p
p
p
p
p
Se tiene:
__
2
5
__
2
4
__
2
3
__
2
2
__
2
1
8548
.
199
9120
.
120
6853
.
61
0336
.
22
5156
.
3
m
EI
L
W
m
EI
L
W
m
EI
L
W
m
EI
L
W
m
EI
L
W
n
n
n
n
n
(10.45)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-383-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
373
Finalmente la respuesta en el tiempo se obtiene con la ecuación (10.41)
1
)
(
)
(
)
,
(
j
j
j t
y
x
t
x
Y
EJEMPLO 5
Encontrar la respuesta en el tiempo de una viga de flexión en voladizo, ante el sismo
registrado el 9 de noviembre de 1974 en Perú. Se desea la respuesta en el tiempo en el tope
de la viga. La geometría y masa por unidad de longitud, son:
.
.
.
2694
.
0
.
15
.
.
028
.
231862 2
2
__
2
m
s
T
m
m
L
m
T
EI
SOLUCIÓN
Se consideran los cinco primeros modos para hallar la respuesta en L
x .
1
)
(
)
(
)
,
(
j
j
j t
y
x
t
x
Y
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
,
( 5
5
4
4
3
3
2
2
1
1 t
y
x
t
y
x
t
y
x
t
y
x
t
y
x
t
L
x
Y
El programa vforzadavoladizo encuentra la respuesta en el tope del edificio ante un
sismo definido por un acelerograma. Es importante que las unidades de los datos sean
compatibles. En este caso el acelerograma tiene que estar en m/s
2
. La forma de uso del
programa es:
[des]=vforzadavoladizo (EI,mu,L,Sismo,dt)
EI Valor de la rigidez a flexión de la viga en voladizo.
mu Es el valor de la masa por unidad de longitud
__
m .
L Es la longitud de la viga en voladizo
Sismo Es el nombre del archivo que contiene el acelerograma.
dt Es el incremento de tiempo del archivo del acelerograma.
Para el ejemplo se debe proceder de la siguiente manera:
>> EI=231862.028
>>mu=0.2694
>>L=15
>>load Peru04.dat
>>[des]=vforzadavoladizo (EI,mu,L,Peru04,0.02)
La respuesta en el tiempo se presenta en la figura 10.9. A continuación se lista el
programa.
function [des]=vforzadavoladizo(EI,mu,L,sismo,dt)
%
% Cálculo de la respuesta en el tiempo, de una viga de flexión
% en voladizo. Cálculo de desplazamiento en el tope del voladizo](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-384-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
374
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [des]=vforzadavoladizo(EI,mu,L,sismo,dt)
%-------------------------------------------------------------
% L : Longitud del elemento
% EI : es la rigidez a flexion de la viga en voladizo
% mu : es la masa por unidad de longitud de la viga en voladizo
% sismo : es el vector que contiene al archivo del acelerograma.
% dt : incremento de tiempo del acelerograma.
% des : desplazamiento en el tope del voladizo
% Las cinco primeras raices de: 1+cos(p)*cosh(p)=0
% son: p1=1.875 p2=4.694 p3=7.854 p4=10.996 p5=14.137
%
% Constantes de Integracion
p1=1.875;a1=p1/L;dx=L/100; p2=4.694; a2=p2/L; p3=7.854; a3=p3/L;
p4=10.996; a4=p4/L; p5=14.137; a5=p5/L;
A=1; C=-1; D1=(cos(p1)+cosh(p1))/(sinh(p1)-sin(p1));B1=-D1;
D2=(cos(p2)+cosh(p2))/(sinh(p2)-sin(p2));B2=-D2;
D3=(cos(p3)+cosh(p3))/(sinh(p3)-sin(p3));B3=-D3;
D4=(cos(p4)+cosh(p4))/(sinh(p4)-sin(p4));B4=-D4;
D5=(cos(p5)+cosh(p5))/(sinh(p5)-sin(p5));B5=-D5;
% Calculo de Integrales donde interviene accion sismica
np=length(sismo);tmax=dt*np;t=linspace(0,tmax,np)';
for i=1:np
F1(i)=sismo(i)*cos(i*dt);F2(i)=sismo(i)*sin(i*dt);
end
F1=F1';F2=F2';INT1=trapz(t,F1);INT2=trapz(t,F2);
% Calculo de frecuencias de los cinco primeros modos
aux1=sqrt(EI/mu); aux2=1/(L*L); aux=aux1*aux2; Wn1=3.5156*aux;
Wn2=22.0336*aux; Wn3=61.6853*aux; Wn4=120.912*aux; Wn5=199.8548*aux;
% Calculo de numerador que contiene al acelerograma para 5 primeros modos
for i=1:np
NSIS1(i)=sin(Wn1*i*dt)*INT1-cos(Wn1*i*dt)*INT2;
NSIS2(i)=sin(Wn2*i*dt)*INT1-cos(Wn2*i*dt)*INT2;
NSIS3(i)=sin(Wn3*i*dt)*INT1-cos(Wn3*i*dt)*INT2;
NSIS4(i)=sin(Wn4*i*dt)*INT1-cos(Wn4*i*dt)*INT2;
NSIS5(i)=sin(Wn5*i*dt)*INT1-cos(Wn5*i*dt)*INT2;
end
% Cálculo de la Integral del denominador en funcion del modo de vibracion
for i=1:100
x(i)=i*dx;
v1(i)=A*sin(x(i)*a1)+B1*cos(x(i)*a1)+C*sinh(x(i)*a1)+D1*cosh(x(i)*a1);
v2(i)=A*sin(x(i)*a2)+B2*cos(x(i)*a2)+C*sinh(x(i)*a2)+D2*cosh(x(i)*a2);
v3(i)=A*sin(x(i)*a3)+B3*cos(x(i)*a3)+C*sinh(x(i)*a3)+D3*cosh(x(i)*a3);
v4(i)=A*sin(x(i)*a4)+B4*cos(x(i)*a4)+C*sinh(x(i)*a4)+D4*cosh(x(i)*a4);
v5(i)=A*sin(x(i)*a5)+B5*cos(x(i)*a5)+C*sinh(x(i)*a5)+D5*cosh(x(i)*a5);
v1(i)=v1(i)*mu; v2(i)=v2(i)*mu; v3(i)=v3(i)*mu; v4(i)=v4(i)*mu; v5(i)=v5(i)*mu;
end
INT31=trapz(x,v1);INT32=trapz(x,v2);INT33=trapz(x,v3);
INT34=trapz(x,v4);INT35=trapz(x,v5);
% Masas modales
aux3=mu*L;
Mj1=0.6130*aux3; Mj2=0.1882*aux3; Mj3=0.0648*aux3; Mj4=0.0315*aux3;Mj5=0.0391*aux3;
%Calculo de y(t)
FAC1=-Mj1/(Wn1*INT31);FAC2=-Mj2/(Wn2*INT32);FAC3=-Mj3/(Wn3*INT33);](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-385-320.jpg)






![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
381
Figura 11.4 Modos de vibración de una viga de corte en voladizo.
En la figura 11.4 se presentan los tres primeros modos de vibración de la viga de corte,
en voladizo. Esta figura fue realizada con el programa vlibrevigacorte, que se utiliza de la
siguiente manera:
[V]=vlibrevigacorte (L)
L Es la longitud del elemento.
function [V]=vlibrevigacorte(L)
%
% Vibraciones libres en un sistema continuo de una viga de corte en voladizo
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [v]=vlibrevigacorte(L)
%-------------------------------------------------------------
% L : Longitud del elemento
% Las tres primeras raices son:
% p1=1.5708 p2=4.7124 p3=7.854
% p=aL
% Constantes de Integracion
p1=1.578;a1=p1/L;dx=L/100; p2=4.7124; a2=p2/L; p3=7.854; a3=p3/L; A=1;
for i=1:100
x(i)=i*dx; v1(i)=A*sin(x(i)*a1); v2(i)=A*sin(x(i)*a2);v3(i)=A*sin(x(i)*a3);
end
hold off
plot(v1,x,'--'); hold on
plot(v2,x,':'); plot(v3,x,'-.')](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-392-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
382
ylabel('Altura'); title('Formas modales de una viga de corte')
hold off
%---fin---
11.2.2 Comparación de formas modales
EJEMPLO 2
Presentar en un grafico el primer modo de vibración de una viga de flexión y de una
viga de corte, en voladizo.
SOLUCIÓN
En la figura 11.5 se presenta el primer modo de vibración de una viga de corte en la
cual se aprecia que en la parte inferior tiene mayores amplitudes que la viga de flexión y en la
parte superior se tiene mayores amplitudes en la viga de flexión que en la de corte.
Este ejemplo es muy ilustrativo del comportamiento de las estructuras e indica que los
edificios compuestos únicamente por vigas y columnas tienen mayores desplazamientos en
los pisos inferiores que un edificio solo con muros de corte pero en la parte superior el
comportamiento es al revés, de ahí que lo ideal es tener una combinación entre el
comportamiento de una viga de flexión con una viga de corte. El programa que compara los
modos de vibración se denomina: vlibrecomparacion y se utiliza de la siguiente manera:
[A]=vlibrecomparacion (L)
L Es la longitud del elemento
function [A]=vlibrecomparacion(L)
%
% Comparacion del primer modo de vibracion de una viga de flexion
% y del primer modo de vibracion de una viga de corte.
% Normalizados en los dos casos a la unidad en el tope del voladizo
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [A]=vlibrecomparacion(L)
%-------------------------------------------------------------
% L : Longitud del elemento
% Viga de flexion
p1=1.875;a1=p1/L;dx=L/100;
A=1; C=-1; D1=(cos(p1)+cosh(p1))/(sinh(p1)-sin(p1));B1=-D1;
for i=1:100
x(i)=i*dx;
vf(i)=A*sin(x(i)*a1)+B1*cos(x(i)*a1)+C*sinh(x(i)*a1)+D1*cosh(x(i)*a1);
end
% Viga de corte
p1=1.578;a1=p1/L; A=1;
for i=1:100
x(i)=i*dx; vc(i)=A*sin(x(i)*a1);
end
hold off
plot(vf,x,'--'); hold on
plot(vc,x,':');
ylabel('Altura'); title('Comparacion de formas modales')](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-393-320.jpg)






![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
389
EJEMPLO 3
Encontrar las cinco primeras frecuencias naturales y sus correspondientes períodos, de
una viga de corte de las siguientes características:
2
2
__
2
2
68
.
0
.
15
36
.
0
08
.
695586
m
Ts
m
m
L
m
A
m
T
G
SOLUCION
Las frecuencias y períodos de vibración, se hallan con las siguientes ecuaciones:
ni
i
ni
W
T
m
GA
L
i
W
2
2
1
2
__
Tabla 11.2 Frecuencias y períodos de vibración
Modo i
ni
W
(1/s)
i
T
(s)
1 58.0110 0.1083
2 174.0330 0.0361
3 290.0549 0.0217
4 406.0769 0.0155
5 522.0989 0.0120
Los resultados obtenidos se indican en la tabla 11.2
EJEMPLO 4
Encontrar la respuesta en el tiempo del cortante basal en los primeros 5 segundos, de
la viga de corte del ejemplo anterior, ante el sismo del 9 de noviembre de 1974, registrado en
Perú, que dura 40 segundos.
Hallar el cortante basal máximo considerando los cinco primeros modos de vibración y
presentar la contribución, al cortante basal, de cada uno de los modos.
2
2
__
2
2
68
.
0
.
15
36
.
0
08
.
695586
m
Ts
m
m
L
m
A
m
T
G
SOLUCIÓN
Para resolver este problema se desarrolló el programa vigacortebasal, cuya forma de
uso es la siguiente:
[Vmax]=vigacortebasal(G,A,mu,L,Sismo,dt)
G Es el módulo de corte de la viga.
A Es el área de la viga de corte.
mu Es el valor de la masa por unidad de longitud
__
m
L Es la longitud de la viga de corte.
Sismo Es el nombre del archivo que contiene el acelerograma.
dt Es el incremento de tiempo en que viene el acelerograma.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-400-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
390
function [Vmax]=vigacortebasal(G,A,mu,L,sismo,dt)
%
% Frecuencias Naturales de una viga de corte en voladizo para
% los cinco primeros modos de vibracion
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [Vmax]=vigacortebasal(G,A,mu,L,sismo,dt)
%-------------------------------------------------------------
% G : Modulo de corte
% A : Area de la seccion transversal de la viga de corte
% mu : Masa por unidad de longitud
% L : Longitud de la viga de corte
% beta : factor de forma por corte se considera igual a 1.2
% sismo: Nombre del archivo que contiene al acelerograma.
% dt : Incremento de tiempo del acelerograma.
beta=1.2;aux1= sqrt((G*A)/(mu*beta)); aux2=pi/(2*L); aux=aux1*aux2;
% Frecuencias Naturales y periodos
Wn1=aux; Wn2=3*aux; Wn3=5*aux; Wn4=7*aux; Wn5=9*aux;
% Calculo de Integrales donde interviene accion sismica
np=length(sismo);tmax=dt*np;t=linspace(0,tmax,np)';
% cambio de unidades del acelerograma de cm/s2 a m/s2
for i=1:np
sismo(i)=sismo(i)/100;
end
for i=1:np
F1(i)=sismo(i)*cos(i*dt);F2(i)=sismo(i)*sin(i*dt);
end
F1=F1';F2=F2';INT1=trapz(t,F1);INT2=trapz(t,F2);
% masas modales
Mt=mu*L;m1=0.811*Mt; m2=0.090*Mt; m3=0.032*Mt; m4=0.017*Mt; m5=0.010*Mt;
FAC1=m1*Wn1;FAC2=m2*Wn2; FAC3=m3*Wn3;FAC4=m4*Wn4;FAC5=m5*Wn5;
% Calculo de numerador que contiene al acelerograma para 5 primeros modos
for i=1:np
NSIS1(i)=sin(Wn1*i*dt)*INT1-cos(Wn1*i*dt)*INT2;
NSIS2(i)=sin(Wn2*i*dt)*INT1-cos(Wn2*i*dt)*INT2;
NSIS3(i)=sin(Wn3*i*dt)*INT1-cos(Wn3*i*dt)*INT2;
NSIS4(i)=sin(Wn4*i*dt)*INT1-cos(Wn4*i*dt)*INT2;
NSIS5(i)=sin(Wn5*i*dt)*INT1-cos(Wn5*i*dt)*INT2;
end
% Calculo del Cortante Basal
Vo=FAC1*NSIS1+FAC2*NSIS2+FAC3*NSIS3+FAC4*NSIS4+FAC5*NSIS5;
plot (t,Vo)
xlabel ('Tiempo'); ylabel ('Cortante Basal')
Vmax=max(abs(Vo))
%---fin---
En la figura 11.6, se presenta la respuesta del cortante en la base para los primeros
cinco segundos. No se indica la respuesta para los 40 segundos debido a que ve una gran
mancha de resultados y no se visualiza bien.
El cortante máximo considerando los cinco primeros modos de vibración es 37.2611 T.,
y en la tabla 11.3 se presentan los cortantes máximos que se obtienen en cada modo de
vibración.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-401-320.jpg)




![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
395
)
(
)
(
)
( '
'
'
'
'
'
z
w
z
u
GA
z
u
EI
Siendo )
(z
u es el desplazamiento en el punto z. Al dividir todo para EI se halla:
EI
z
w
z
u
H
z
u
)
(
)
(
)
( '
'
2
2
'
'
'
'
Donde:
EI
GA
H
c
2
2
Para valores muy pequeños de el comportamiento es de una viga de flexión, para
0
sería viga de flexión. Por el otro lado, para valores muy altos de el comportamiento
es de una viga de corte; concretamente para
es viga de corte. De tal manera que de
acuerdo al valor de se puede tener una viga de flexión o una de corte o una que tenga las
propiedades de las dos.
La forma de distribución de la carga lateral considerada por Miranda, está definida por:
a
H
z
a
e
e
W
z
w
1
1
)
(
/
max
Donde max
W es el valor máximo de la carga distribuida. Mediante el parámetro a se
puede tener variaciones de carga: triangular si 01
.
0
a ; parabólica sí 03
.
2
a ; uniforme
distribuida si a tiene un valor muy alto.
EJEMPLO 1
Presentar la variación de la carga a lo largo de la altura de la viga, para los siguientes
valores de a: 0.01, 2, 5 y 2000. La variación e la carga dividirla para max
W .
SOLUCIÓN
Para resolver el problema se elaboró el programa variacioncarga cuya forma de uso
es la siguiente:
[w]=variacioncarga (a)
a Es un vector que contiene 4 valores de a para los cuales se desea hallar la
variación de la carga.
>>a=[ 0.01; 2; 5; 2000]
>> [w]=variacioncarga(a)
En la figura 12.2 se presenta la variación de la carga para los valores de a solicitados.
(12.7)
(12.8)
(12.9)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-406-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
396
Figura 12.2 Diferentes variaciones de carga transversal
function [w]=variacioncarga(a)
%
% Variacion de la carga en viga de corte acoplada a la flexion
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [w]=variacioncarga(a)
%-------------------------------------------------------------
% a :Parámetro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% Es un vector que se da como dato, el programa obtiene la
% distribucion de carga para 4 valores de a.
% Wmax : intensidad de la carga uniforme distribuida. Programado para 1
dz=0.01; hold off;
for k=1:4
aa=a(k);
for z=1:101
zh=(z-1)*dz;num=1-exp(-aa*zh);den=1-exp(-aa);w(z)=num/den;zz(z)=zh;
end
if k==1
plot(w,zz,'--'); hold on;
elseif k==2
plot(w,zz,':');
elseif k==3
plot(w,zz,'-.');
else
plot(w,zz)
end
end
xlabel ('Valor w(z) / Wmax'); ylabel ('z / H');
%---fin---](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-407-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
397
12.2.1 Respuesta en desplazamiento
La respuesta de la ecuación diferencial (12.7) encontrada por Miranda (1999) para la
variación de carga definida en (12.9) es:
6
5
2
4
/
3
2
1
4
max
cosh
1
)
( C
H
z
C
H
z
C
e
C
H
z
C
H
z
senh
C
e
EI
H
W
z
u H
az
a
Las constantes de integración para la viga en voladizo son:
2
2
3
2
2
3
2
2
1
a
a
a
a
e
a
e
C
a
a
cosh
1
cosh 2
2
4
2
2
2
2
2
3
2
2
3
2
2
2
a
a
e
senh
a
a
a
a
e
e
a
C
a
a
a
2
2
2
3
1
a
a
C
2
4
2
1
C
2
2
2
2
3
2
2
5
a
a
a
a
e
e
a
C
a
a
cosh
1
1
cosh 2
2
4
2
2
2
2
2
2
1
6
a
a
e
a
a
senh
C
C
a
EJEMPLO 2
La viga en voladizo indicada en la figura 12.3 de 15 m., de altura tiene una rigidez
1
EI y sobre ella actúa una carga triangular cuyo valor máximo es 2 T./m., Se desea
presentar un gráfico para la variación del desplazamiento transversal dividido para el
desplazamiento máximo. Para los siguientes valores de : 1; 2; 10 y 50.
SOLUCIÓN
Para resolver este problema se elaboró el programa desplazamientomiranda cuya
forma de uso es la siguiente:
[u] = desplazamiento(Wmax,alfa,H,EI)
Wmax Valor máximo de la carga distribuida.
alfa Vector que contiene los cuatro valores de que definen la estructura.
H Altura de la viga en voladizo.
EI Rigidez a flexión de la viga en voladizo.
(12.10)
(12.11)
(12.12)
(12.13)
(12.14)
(12.15)
(12.16)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-408-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
398
Figura 12.3 Viga en voladizo sometida a carga triangular.
function [u]=desplazamientomiranda(Wmax,alf,H,EI)
%
% Respuesta de una viga de flexion acoplada a una de corte, propuesta
% por Miranda (1999). Valida para vigas de seccion constante.
% Programado para distribucion de carga triangular.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [u]=desplazamientomiranda(Wmax,alf,H,EI)
%-------------------------------------------------------------
% a :Parametro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% Wmax :Intensidad de la carga uniforme distribuida
% alf :Vector que contiene los cuatro valores de alfa para los cuales
% :se encuentra el desplazamiento de la viga
% alfa :Parametro que controla el comportamiento de la viga si es cero
% comporta como una viga de flexion y si es infinito como de corte.
% H :Altura total de la viga de corte acoplada a la de flexion
% EI :Rigidez a flexion de la viga.
%Constantes de Integracion
a=0.01;
for k=1:4
alfa=alf(k);
num1=alfa^2*exp(-a)-a^2*exp(-a)-a^3+a*alfa^2-alfa^2;
den1=a*alfa^3*(a^2-alfa^2); c1=num1/den1;
num21=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2+alfa^2;
num22=alfa^2*exp(-a)+a^2-alfa^2; den2=alfa^4*(a^2-alfa^2);
aux1=num21/den1; aux2=num22/den2;
c2=(aux1*sinh(alfa)/cosh(alfa))+(aux2*(1/cosh(alfa)));
den3=a^2*(a^2-alfa^2); c3=-1/den3;
den4=2*alfa^2; c4=-1/den4;
num5=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2;
den5=a*alfa^2*(a^2-alfa^2); c5=num5/den5;
num6=alfa^2*exp(-a)+a^2-alfa^2; aux3=1/den3;aux4=num6/den2;
aux5=c1*sinh(alfa)/cosh(alfa); aux6=aux4*(1/cosh(alfa));
c6=aux5+aux3-aux6;
z
EI=1 H = 15](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-409-320.jpg)


![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
401
Figura 12.6 Comparación del efecto de aplicación de las cargas.
El programa, elaborado en MATLAB, con el cual se resolvió este ejemplo se llama:
comparaciondesplazamiento. Su forma de uso es:
[u] = comparaciondesplazamiento (Wmax,alfa,H,EI)
Wmax es la carga máxima por unidad de longitud.
alfa es el valor que define el comportamiento estructural.
H es la altura de la viga en voladizo.
EI es la rigidez a flexión de la viga en voladizo.
function [u]=comparaciondesplazamiento(Wmax,alfa,H,EI)
%
% Compara los desplazamientos laterales de una viga en voladizo
% ante carga triangular y carga uniforme distribuida.
% Utilizando desarrollo numerico de Miranda (1999).
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [u]=comparaciondesplazamiento(Wmax,alfa,H,EI)
%-------------------------------------------------------------
% a :Parametro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% Wmax :Intensidad de la carga uniforme distribuida
% alfa :Parametro que controla el comportamiento de la viga si es cero
% comporta como una viga de flexion y si es infinito como de corte.
% H :Altura total de la viga de corte acoplada a la de flexion
% EI :Rigidez a flexion de la viga.
%Constantes de Integracion
aa(1)=0.01; aa(2)=2000;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-412-320.jpg)


![SISTEMAS DE UN GRADO DE LIBERTAD
404
SOLUCIÓN
Antes de presentar el programa betauno con el cual se hallan las curvas pedidas,
veamos como se procedería para el caso de un edificio de 2 pisos. En este caso la altura total
es 6
H m. Por lo tanto se debe evaluar .)
0
.
3
( 1 m
z
y
.
0
.
6
2 m
z
con la ecuación
(12.21) . Luego de lo cual se realiza la sumatoria de la ecuación ( 12.19 ) para hallar 1
. La
forma de uso del programa betauno es la siguiente:
[beta]=betauno(alfa)
alfa Es un vector que contiene los valores de para los cuales se desean hallar
las curvas de 1
.
>> alfa = [ 2; 4; 8; 30 ]
>> [beta]=betauno(alfa)
function [beta]=betauno(alf)
%
% Calculo del parametro beta1 utilizando el modelo de Miranda (1999)
% Obtiene la curva para 1 a 10 pisos para varios valores de alfa.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [beta]=betauno(alf)
%-------------------------------------------------------------
% a :Parametro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% alf : Vector de datos de alfa que da el usuario.
% alfa :Parametro que controla el comportamiento de la viga si es cero
% comporta como una viga de flexion y si es infinito como de corte.
% H :Altura total de la viga de corte acoplada a la de flexion
% N :Numero de pisos
KT=length(alf); a=0.01;hold off
for K=1:KT;
alfa=alf(K);
%Constantes de Integracion
num1=alfa^2*exp(-a)-a^2*exp(-a)-a^3+a*alfa^2-alfa^2;
den1=a*alfa^3*(a^2-alfa^2); c1=num1/den1;
num21=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2+alfa^2;
num22=alfa^2*exp(-a)+a^2-alfa^2; den2=alfa^4*(a^2-alfa^2);
aux1=num21/den1; aux2=num22/den2;
c2=(aux1*sinh(alfa)/cosh(alfa))+(aux2*(1/cosh(alfa)));
den3=a^2*(a^2-alfa^2); c3=-1/den3;
den4=2*alfa^2; c4=-1/den4;
num5=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2;
den5=a*alfa^2*(a^2-alfa^2); c5=num5/den5;
num6=alfa^2*exp(-a)+a^2-alfa^2; aux3=1/den3;aux4=num6/den2;
aux5=c1*sinh(alfa)/cosh(alfa); aux6=aux4*(1/cosh(alfa));
c6=aux5+aux3-aux6
% Calculo de denominador
denominador=c1*sinh(alfa)+c2*cosh(alfa)+c3*exp(-a)+c4+c5+c6;
% Calculo del numerador
for N=1:20
H=3*N;dz=H/N;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-415-320.jpg)


![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
407
12.3.2 Desplazamiento lateral
La ecuación (12.17) sirve para encontrar la respuesta elástica, en desplazamientos, de
un edificio ante un espectro elástico. En este sub apartado interesa encontrar la relación
j
d
S
z
u
1
/
)
( para ver como varían los desplazamientos en diferentes estructuras
caracterizadas por el valor .
EJEMPLO 6
Encontrar la relación d
S
z
u /
)
( para cuatro estructuras definidas por los siguientes
valores de : 0.5; 3; 8 y 30. Considerando que son edificios de 20 pisos. Calcular con la
función j
normalizada a unidad en el tope.
SOLUCIÓN
En la figura 12.9 se presenta la respuesta del problema, la misma que se encontró con
el programa desplazamientolateral que se utiliza de la siguiente forma:
[u] = desplazamientolateral (N,alfa)
N es el número de pisos.
Alfa es el vector que contiene los valores de .
Para el ejemplo se tiene:
>> alfa=[0.5; 3; 8; 30]
>> desplazamientolateral (20,alfa)
Figura 12.9 Variación del desplazamiento en altura para diferentes estructuras.](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-418-320.jpg)
![SISTEMAS DE UN GRADO DE LIBERTAD
408
Es interesante notar en la figura 12.9 que existe un punto en 85
.
0
/
H
z que define
el comportamiento para valores menores y para valores mayores. Es como un punto de
inflexión donde cambia el comportamiento de las estructuras, las que se deforman menos
antes de este valor a partir de este punto se deforman más.
function [u]=desplazamientolateral(N,alf)
%
% Determina la variacion del desplazamiento lateral en altura, como un
% sistema continuo para diferentes valores de alfa. Utilizando el modelo
% propuesto por Miranda (1999)
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [u]=desplazamientolateral(N,alf)
%-------------------------------------------------------------
% a :Parametro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% alf : Vector de datos de alfa que da el usuario.
% alfa :Parametro que controla el comportamiento de la viga si es cero
% comporta como una viga de flexion y si es infinito como de corte.
% H :Altura total de la viga de corte acoplada a la de flexion
% N :Numero de pisos
% Este programa calcula: u(z)/Sd = beta1 * La forma modal
KT=length(alf); a=0.01;hold off
for K=1:KT;
alfa=alf(K);
%Constantes de Integracion
num1=alfa^2*exp(-a)-a^2*exp(-a)-a^3+a*alfa^2-alfa^2;
den1=a*alfa^3*(a^2-alfa^2); c1=num1/den1;
num21=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2+alfa^2;
num22=alfa^2*exp(-a)+a^2-alfa^2; den2=alfa^4*(a^2-alfa^2);
aux1=num21/den1; aux2=num22/den2;
c2=(aux1*sinh(alfa)/cosh(alfa))+(aux2*(1/cosh(alfa)));
den3=a^2*(a^2-alfa^2); c3=-1/den3;
den4=2*alfa^2; c4=-1/den4;
num5=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2;
den5=a*alfa^2*(a^2-alfa^2); c5=num5/den5;
num6=alfa^2*exp(-a)+a^2-alfa^2; aux3=1/den3;aux4=num6/den2;
aux5=c1*sinh(alfa)/cosh(alfa); aux6=aux4*(1/cosh(alfa));
c6=aux5+aux3-aux6;
% Calculo de denominador
denominador=c1*sinh(alfa)+c2*cosh(alfa)+c3*exp(-a)+c4+c5+c6;
% Calculo del numerador
H=3*N;dz=H/N;
for z=1:N
zh=z*dz; coef1=c1*sinh(alfa*zh/H)+c2*cosh(alfa*zh/H)+c3*exp(-a*zh/H);
coef2=c4*(zh/H)^2+c5*(zh/H)+c6; si(z)=(coef1+coef2)/denominador;
end
% Calculo de sumatorias
sumn=0; sumd=0;
for z=1:N
sumn=sumn+si(z); sumd=sumd+si(z)*si(z);
end
beta=sumn/sumd;
dz=0.01;](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-419-320.jpg)

![SISTEMAS DE UN GRADO DE LIBERTAD
410
La deriva de piso es aproximadamente igual a la derivada de u con respecto a z . A
continuación se halla la deriva a lo largo de la viga multiplicada por )
(
/ H
u
H .
6
5
4
3
2
1
5
4
/
3
2
1
cosh
2
cosh
)
(
)
/
(
C
C
C
e
C
C
senh
C
C
H
z
C
e
a
C
H
z
senh
C
H
z
C
H
u
H
dz
H
z
du
a
H
az
EJEMPLO 7
Presentar la variación de la deriva de piso normalizada por el producto )
(
/ H
u
H para
valores de : 2; 5; 10 y 30. El valor del desplazamiento en el último piso dividido para la altura
total es la deriva global, luego lo que se pide en el ejercicio es la relación entre la deriva de piso
dividida para la deriva global.
SOLUCIÓN
En la figura 12.10 se presenta la variación de la deriva de piso solicitada. Nótese que
los mayores valores se hallan para valores de 5
.
0
H
z
es decir en los pisos inferiores.
Figura 12.10 Variación de la deriva a lo largo de la altura.
El programa con el cual se obtiene la figura 12.10 se denomina: variacionderiva y la
forma de uso es la siguiente:
[u] = variacionderiva (alfa)
alfa es el vector que contiene los valores de
La entrada de datos para el ejemplo es la siguiente:
( 12.24 )](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-421-320.jpg)
![ROBERTO AGUIAR FALCONI
CEINCI-ESPE
411
>> alfa = [ 2; 5; 10; 30]
>> [u] = variacionderiva (alfa)
function [u]=variacionderiva(alf)
%
% Determina la variacion de la deriva de piso con la altura, multiplicada
% por H/u(H). Trabajo de Miranda (1999) Calcula la variacion de la deriva
% para varios valores de alfa.
%
% Por: Roberto Aguiar Falconi
% CEINCI-ESPE
%-------------------------------------------------------------
% [u]=variacionderiva(alf)
%-------------------------------------------------------------
% a :Parametro que define la variacion de la carga a=0.01 es
% triangular y a= infinito es carga uniforme distribuida.
% alf : Vector de datos de alfa que da el usuario.
% alfa :Parametro que controla el comportamiento de la viga si es cero
% comporta como una viga de flexion y si es infinito como de corte.
% H :Altura total de la viga de corte acoplada a la de flexion
% N :Numero de pisos
% Este programa calcula: u(z)/Sd = beta1 * La forma modal
KT=length(alf); a=0.01;hold off
for K=1:KT;
alfa=alf(K);
%Constantes de Integracion
num1=alfa^2*exp(-a)-a^2*exp(-a)-a^3+a*alfa^2-alfa^2;
den1=a*alfa^3*(a^2-alfa^2); c1=num1/den1;
num21=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2+alfa^2;
num22=alfa^2*exp(-a)+a^2-alfa^2; den2=alfa^4*(a^2-alfa^2);
aux1=num21/den1; aux2=num22/den2;
c2=(aux1*sinh(alfa)/cosh(alfa))+(aux2*(1/cosh(alfa)));
den3=a^2*(a^2-alfa^2); c3=-1/den3;
den4=2*alfa^2; c4=-1/den4;
num5=a^2*exp(-a)-alfa^2*exp(-a)+a^3-a*alfa^2;
den5=a*alfa^2*(a^2-alfa^2); c5=num5/den5;
num6=alfa^2*exp(-a)+a^2-alfa^2; aux3=1/den3;aux4=num6/den2;
aux5=c1*sinh(alfa)/cosh(alfa); aux6=aux4*(1/cosh(alfa));
c6=aux5+aux3-aux6;
% Calculo de denominador
denominador=c1*sinh(alfa)+c2*cosh(alfa)+c3*exp(-a)+c4+c5+c6;
% Calculo del numerador
dz=0.01;
for z=1:101
zh=(z-1)*dz;
coef1=c1*alfa*cosh(alfa*zh)+c2*alfa*sinh(alfa*zh)-c3*a*exp(-a*zh);
coef2=2*c4*zh+c5; u(z)=(coef1+coef2)/denominador;y(z)=zh;
end
if K==1
plot(u,y,'--'); hold on;
elseif K==2
plot(u,y,'-.')
elseif K==3
plot(u,y,':')
else
plot(u,y)](https://image.slidesharecdn.com/librodinamicadeestructuras-220419023418/85/LIBRODINAMICADEESTRUCTURAS-pdf-422-320.jpg)




