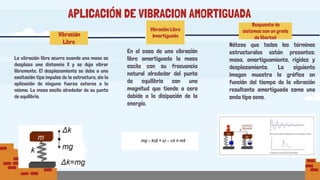
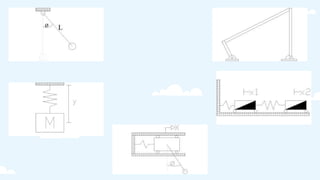
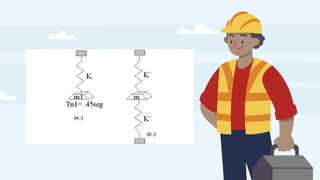
Este documento trata sobre la aplicación de vibración libre amortiguada, rigidez lateral de pórticos y muros de albañilería de un grado de libertad. Explica conceptos como vibración libre, amortiguamiento, rigidez lateral y sistemas con un grado de libertad. También analiza ejemplos numéricos y concluye enfatizando la importancia de considerar aspectos sísmicos y de amortiguamiento en la construcción peruana debido al alto riesgo sísmico del país.

1. APLICACIÓN DE VIBRACIÓN LIBRE AMORTIGUADA, RIGIDEZ LATERAL DE
PÓRTICOS Y MUROS DE ALBAÑILERÍA DE UN GRADO DE LIBERTAD,
RESPUESTA DE SISTEMAS CON UN GRADO DE LIBERTAD”.
DOCENTE
• ING. PINEDO DELGADO ANDRES
INTEGRANTES:
• ROJAS MOZOMBITE, Hia Malu
• SOTO FLORES, Raúl Jesús
• MORALES VASQUEZ Jheyson
CURSO:
INGENIERIA SISMICA
2022

2. INTRODUCCION
En el informe de investigación se verá la aplicación de vibración libre
amortiguada, rigidez lateral de pórticos y muros de albañilería de un
grado de libertad, respuesta de sistemas con un grado de libertad y
conceptos iniciales importantes para el estudio de las vibraciones
mecánicas.
Es importante conocer la clasificación de las vibraciones mecánicas ya
que nos presentan un panorama de los diferentes estudios.

3. APLICACIÓN DE VIBRACION AMORTIGUADA
La vibración libre ocurre cuando una masa se
desplaza una distancia X y se deja vibrar
libremente. El desplazamiento se debe a una
excitación tipo impulso de la estructura, sin la
aplicación de ninguna fuerza externa a la
misma. La masa oscila alrededor de su punto
de equilibrio.
En el caso de una vibración
libre amortiguada la masa
oscila con su frecuencia
natural alrededor del punto
de equilibrio con una
magnitud que tiende a cero
debido a la disipación de la
energía.
Nótese que todos los términos
estructurales están presentes:
masa, amortiguamiento, rigidez y
desplazamiento. La siguiente
imagen muestra la gráfica en
función del tiempo de la vibración
resultante amortiguada como una
onda tipo seno.
Vibración
Libre
Vibración Libre
Amortiguada
Respuesta de
sistemas con un grado
de libertad

4. RIGIDEZ LATERAL DE PORTICOS
La deformación axial de los elementos no se considera
apreciable, de modo que los tres grados de libertad del
sistema consisten en un desplazamiento lateral y dos
giros en los nudos superiores.

5. Matriz de Rigidez Lateral de un
Pórtico de Varios Pisos
En un pórtico de varios pisos, la matriz de rigidez total es una
operación repetitiva de ensambles de matrices de los elementos,
sean estas vigas, columnas, muros o arriostres.

6. Vibración lineal: Si los
componentes básicos de un
sistema tienen un
comportamiento lineal la
vibración resultante es lineal.
Vibración no lineal: Se
produce si alguno de sus
componentes se comporta
como no lineal.
El comportamiento lineal de un
elemento facilita su estudio, en
la realidad todo elemento de
comporta como no lineal pero
los resultados de su estudio no
difieren, en su mayoría, a los
realizados si se consideran
como elementos lineales.

7. Si las características de señal de la vibración de un
sistema se asemejan a una señal senoide, entonces se
dice que la vibración es senoide.
Una señal compleja a simple vista no se pude
representar por medio de una ecuación matemática,
pero si puede ser determinado por medio de senos y
cosenos.

8. METODOS PARA EL CALCULO DE ECUACIONES DIFERENCIALES DE SISTEMAS
LIBRES NO AMORTIGUADOS
Algunos sistemas vibratorios pueden ser expresados a la forma
canónica y posteriormente calcular su frecuencia natural y/o
respuesta en el tiempo.
Movimiento rectilíneo 1° método de Newton F = ma
Movimiento angular 2° método de Newton (momentos)
Movimiento rect. y/o angular o método de energía.
Por lo tanto, el primer tipo es identificar el tipo de movimiento para ver el método
apropiado para calcular la ecuación diferencial.
Si el sistema posee movimiento rectilíneo utilizar el análisis cinético S (fy = S fy efect =
mx) es apropiado solo hay que llegar a la ecuación diferencial del movimiento.

9. . ESTRUCTURA CON 1 GDL
Una deformada estructural a lo largo de un eje.
Una frecuencia de resonancia.
Una masa condensada constituyendo un nodo de la estructura.
Una estructura con un único GDL tiene un solo modo de vibración y se caracteriza
por:

11. Ejemplo
Un resorte de constante elástica ‘K’ es empotrado de un extremo
mientras que el otro extremo se coloca una masa de 4.53 kg
logrando tener un periodo natural de 0.45 seg. Posteriormente el
resorte se parte justo a la mitad empotrándose de los extremos y
colocando la masa en el punto medio. Calcule el periodo natural
nuevo.

13. Analizando el sistema (b)
Para ver cómo afecta la constante al dividirse
a la mitad partimos de la fórmula para
calcular la constante en función de sus
características
K= Gd4 n = # vueltas k’ = Gd4 = 2K K’= 2K
64R3n 64R3(n/2)
cómo están en paralelo
Keq= K’ + K’ = 2K +2K = 4K Keq = 4 (882.25) =
3526 Nw/mt
Wn = √Keq = √3526 = 88.22 rad/seg
√m √0.453
un elemento elástico de constante
desconocida sufre una deformación estática
‘Xs’ al colocarle una masa ‘m’. calcule la
frecuencia natural.
Solución:
Aquí no es necesario hacer un análisis
Cinético ya que la ecuación Diferencial
es directa.
0.453 x + kx
vamos a analizar los sistemas por
separado analizando el sistema (a)
Wn = √K = √K è K=Wn12 m = (13.95)2
(4.53)
√m 0.453 k=887.54 Nw/m
Solución:
La constante elástica k se
puede calcular a partir de la
ley de Hooke mg= KXs
k=mg/xs sustituyéndolo en la
fórmula de la frecuencia
natural.
Wn = √K = √mg = √g Wn = √g
√m √mxs √xs √xs

14. AMORTIGUAMIENTO DE ESTRUCTURAS
Consiste en suspender una enorme masa cerca de la parte superior
de la estructura. Los cables de acero soportan la masa, mientras
que los amortiguadores de fluido viscoso se encuentran entre la
masa y el edificio que está tratando de proteger.
Amortiguadores de rendimiento metálico
En los amortiguadores de deformación la energía es absorbida por
los componentes metálicos que ceden con lo que se reduce la
demanda de disipación de energía en los miembros estructurales
primarios y se minimiza el posible daño estructural.

15. La construcción de un amortiguador viscoso o de
fluidos se parece al amortiguador común que se
encuentra en los automóviles. El pistón transmite
energía moviendo el fluido en el regulador, este
movimiento del fluido absorbe la energía cinética
convirtiéndola en calor.

16. CONCLUSIONES
Previo al diseño estructural de cualquier tipo de edificación, en
especial los
edificios abiertos; ya que en los pórticos que forman parte de
estas paredes la
mampostería abarca el 100 % por la ausencia de ventanas,
puertas y balcones;
al momento de que no se toma en cuenta ésta mampostería
Sin embargo los sistemas de amortiguación en las
estructuras no solo deben aplicarse en obras de gran
magnitud sino que tambien deben ser mas usuales en
obras pequeñas ya que no llevan un control muchas
veces por parte de un profesional .

17. CONCLUSIONES
El Perú es un país de alto riesgo sísmico sujeto a distintos tipos
de desastres, ya que las personas a cargo de distintos tipos de
construcciones deben tener en cuenta ese aspecto para tomar
las medidas y prevenciones necesarias al momento de ejecutar
cualquier tipo de estructuras asegurando la integridad y
seguridad de las personas.