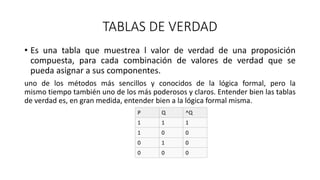
El documento resume conceptos clave de lógica matemática como proposiciones, conectivos lógicos, proposiciones condicionales y bicondicionales, tautologías, equivalencias y contradicciones. También describe métodos de demostración como el directo e indirecto e introduce tablas de verdad como una herramienta para evaluar proposiciones compuestas.

2. Concepto de lógica matemática
Definición y clase de proposiciones
Conectivos lógicos en proposiciones compuestas
Proposiciones condicionales
Proposiciones bicondicional
Tecnología, equivalencia y contradicción
Leyes notables en lógica
Métodos de demostración
Tablas de verdad

3. LOGICA MATEMATICA
CONCEPTO
•
EJEMPLOS
Es la disciplina que trata de métodos de
razonamiento. En un nivel elemental, la
lógica proporciona reglas y técnicas para
determinar si es o no valido un
argumento dado.
• Todos los españoles son europeos,
Shakespeare no era español, luego
Shakespeare no era europeo. no es
un razonamiento valido,1 pues las
premisas son verdaderas y, pese a
ello, la conclusión es falsa. Aquí es
crucial entender que, para que un
razonamiento sea valido, (si parte
de premisas verdaderas) no basta
con que sus conclusiones sean
verdaderas, sino que tienen que
ser necesariamente verdaderas.

4. PROPOSICIONES
DEFINICION
• es una oración con valor
referencial o informativo, de la
cual se puede predicar su
veracidad o falsedad, es decir,
que puede ser falsa o verdadera
pero no ambas a la vez.
CLASES
• Proposiciones Simples:
• Son aquellas que no tienen oraciones
componentes afectadas por negaciones
(“no”) o términos de enlace como
conjunciones (“y”), disyunciones (“o”) o
implicaciones (“si . . . entonces”). Pueden
aparecer términos de enlace en el sujeto o
en el predicado, pero no entre oraciones.
• Proposiciones Compuestas:
• Una proposición será compuesta si no es
simple. Es decir, si está afectada por
negaciones o términos de enlace entre
oraciones componentes.

5. CONECTORES LOGICOS EN PROPOSICIONES
COMPUESTAS
• Los conectores lógicos son ciertas palabras y/o expresiones cuya
función en el discurso es enlazar las distintas ideas que puede
contener una oración, un párrafo o un texto, de manera fluida y
comprensible, pero además incorporando una relación determinada
de sentido entre ellas.
Existen conectores u operadores lógicas que permiten formar
proposiciones compuestas(formadas por varias proposiciones).

6. PROPOSICION CONDICIONAL
El condicional es una proposición
compuesta formada por dos
proposiciones simples, ligadas por el
conectivo si ..., entonces... Si las
proposiciones
se denominan p y q, el condiional se
escribe . p se llama antecedente y q
se llama consecuente.

7. PROPOSICION BICONDICIONAL
El condicional es una proposición compuesta formada por dos
proposiciones simples, ligadas por el conectivo si ...,
entonces... Si las proposiciones se denominan p y q, el condiional
se escribe . p se llama antecedente y q se llama
consecuente.

8. TAUTOLOGIA,EQUIVALENCIA Y
CONTRADICCIÓN
• Tautología: Es una expresión lógica que resulta verdadera para
cualquier interpretación; es decir, para cualquier asignación de
valores de verdad.
• Contradicción: Si una proposición compuesta es falsa para todas las
asignaciones entonces es una contradicción.
• Equivalencia: Se dice que dos proposiciones son lógicamente
equivalentes, o simplemente equivalentes. Si coinciden sus resultados
para los mismos valores de verdad.

9. LEYES NOTABLES EN LOGICA
• Ley de doble negación: Dentro de un sistema de lógica clásica, la doble negación, esto es, la negación de la negación de
una proposición p, es lógicamente equivalente a p. Expresado simbólicamente, ¬(¬p) ⇔ p. En lógica intuicionista, una
proposición implica su doble negación, pero no al revés. Esto marca una importante diferencia entre la negación clásica e
intuicionista. Algebraicamente, la negación clásica es llamada una involución de periodo dos.
• Leyes de idempotencia: En matemática y lógica, la idempotencia es la propiedad para realizar una acción determinada
varias veces y aun así conseguir el mismo resultado que se obtendría si se realizase una sola vez. Un elemento que cumple
esta propiedad es un elemento idempotente, o un idempotente.
• Leyes asociativas: Las "Leyes asociativas" quieren decir que no importa cómo agrupes los números (o sea, qué calculas
primero) cuando sumas o cuando multiplicas.(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c)
• Leyes conmutativas:Las "leyes conmutativas" sólo quieren decir que puedes intercambiar los números
cuando sumas o cuando multiplicas y la respuesta va a ser la misma.a + b = b + a
a × b = b × a
• Leyes distributivas:La "ley distributiva" es la MEJOR de todas, pero hay que usarla con
mucho cuidado Quiere decir que la respuesta es la misma cuando:sumas varios números
y el resultado lo multiplicas por algo, o haces cada multiplicación por separado y
luego sumas los resultados
• Así:(a + b) × c = a × c + b × c

10. METODOS DE DEMOSTRACIÓN
• Es una cadena finita de proposiciones verdaderas, que se obtienen con ayuda de
reglas de inferencia lógicas. El punto de partida de esta cadena son proposiciones
cuya verdad es conocida. El punto final de la cadena es el teorema a demostrar.
• El Método Directo :Consiste en partir de las premisas (datos) del teorema y
aplicando las reglas de la lógica y la teoría desarrollada, obtener o llegar a
la tesis (conclusión) del teorema después de un número finito de pasos.
• El Método Indirecto: Consiste en negar la tesis del teorema y a partir de esta
proposición y con ayuda de las reglas de la lógica y la teoría desarrollada
encontrar una contradicción respecto a las premisas, una proposición verdadera
o respecto a la suposición.
• Demostraciones por Inducción Completa : Es un método especial de
demostración matemática que permite, a base de observaciones particulares,
juzgar de las regularidades generales correspondientes.

11. TABLAS DE VERDAD
• Es una tabla que muestrea l valor de verdad de una proposición
compuesta, para cada combinación de valores de verdad que se
pueda asignar a sus componentes.
uno de los métodos más sencillos y conocidos de la lógica formal, pero la
mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas
de verdad es, en gran medida, entender bien a la lógica formal misma.
P Q ^Q
1 1 1
1 0 0
0 1 0
0 0 0