Este documento presenta un resumen del curso de Matemática Aplicada a la Medicina impartido en 2010. Incluye contenidos como lógica y conjuntos, análisis combinatorio y probabilidades, sistemas de números reales y relaciones y funciones. También explica conceptos de lógica proposicional como enunciados, proposiciones, conectivos lógicos, tablas de verdad y cuantificadores.

1. ASIGNATURA: Matemática aplicada a la Medicina 2010 JEFE DEL CURSO: Dr. Félix Peña Palomino

2. CONTENIDO Lógica y Conjuntos Análisis combinatorio y probabilidades Sistema de números reales Relaciones y funciones. Logaritmos y exponenciales. Mediciones y magnitudes.

3. Lógica Proposicional Enunciado abierto Son expresiones que contienen variables y que no tienen propiedad de ser verdaderos o falsos. Ejemplo: x+3 = 8 ; El tiene 20 años Enunciado: Es toda frase u oración que se emite. Algunos enunciados indican expresiones imperativas, exclamativas, interrogativas; otros en cambio pueden ser verdaderos o falsos. Ejemplo: ¿Qué hora es? , ¡Arriba Perú! La matemática es fácil. x + 4 = 6

4. Proposición : Es toda expresión que tiene la propiedad de ser verdadera o falsa. Ejemplo: Notación . Generalmente a las proposiciones se les denota por letras minúsculas tales como: p, q, r, .. Así : P: Luis estudia ; q : Luis trabaja Juan estudia medicina en la USMP. 2 + 5 = 8 Si estudio matemática, entonces apruebo el examen. Mario Vargas Llosa nació en Arequipa.

5. Conectivos lógicos: p : Luis estudia q : Luis trabaja : Luis estudia “y” trabaja Son expresiones que enlazan dos o más proposiciones Entre estas , se tiene: “o”; “y” ; “entonces”, “implica”; “ si y solo si”, etc. Los conectivos lógicos que usaremos son: La Conjunción Enlaza dos o más proposiciones con la palabra “y”, denotado por Ejemplo:

6. Su tabla de verdad es: La conjunción sólo es verdadera, cuando las dos proposiciones son verdaderas F F F F V F F F V V V V p q q p

7. La Disyunción: Relaciona dos o más proposiciones con la palabra “0”; que se denota por “ “ Su tabla de verdad es: La disyunción sólo es falsa, cuando ambas proposiciones son falsas. F F F V V F V F V V V V p q q p

8. La disyunción exclusiva o diferencia simétrica La disyunción exclusiva, sólo admite que es verdadera, si una de las proposiciones es verdadera y la otra es falsa. Se denota por: Se lee: “p o q pero no ambos ” “ o es p o es q” p: Víctor Raúl nació en Trujillo. q: Víctor Raúl nació en Lima. “ o Víctor Raúl nació en Trujillo o en Lima” F F F V V F V F V F V V p q q p

9. La negación : La negación de una proposición “p”, es otra proposición , denotado por “ ~ p”, que se lee: “no p” , o “no es cierto que”, cuya verdad o falsedad queda determinada por la siguiente tabla: Ejemplo: P: Pedro es estudioso ~p: Pedro no es estudioso, o también: No es cierto que Pedro es estudioso V F F V ~p p

10. El condicional: En el condicional: p q “ p” se llama antecedente “ q” se llama consecuente Denotado por el símbolo: se lee: “Entonces” o “implica”, etc. Por lo tanto, este conectivo une dos o más proposiciones con la palabra “entonces” Ejemplo: p: Juan estudia q: Juan aprueba el examen p q : Si Juan estudia, entonces aprueba el examen.

11. Su tabla de verdad es: Nota : En el condicional: Sólo, es falso, cuando el antecedente es verdadero y el consecuente es falso; en todo los demás casos es verdadero. p q V F F V V F F F V V V V p ⇒ q q p

12. Al condicional se le asocia tres expresiones lógicas importantes: Sea el condicional: p ⇒q La proposición Recíproca es: q ⇒ p La proposición inversa es: ~p ⇒ ~ q La Contrarrecíproca es: ~q ⇒ ~p Construyendo la tabla de verdad, se tiene: Directo Rcíproco Inversa Contrarecíproco V V V V F F V F F V F V F V V F V F V V V V V V p q

13. El Bicondicional o Doble implicación Denotado por: Se lee: “Sí y sólo sí”. Relaciona dos o más proposiciones mediante la palabra “sí y sólo si”. Su tabla de verdad es: p: Londres está en Inglaterra q: París está en Francia. Londres está en Inglaterra si, y solamente si, París está en Francia. V F F F V F F F V V V V q p

14. Cálculo de valores de verdad de fórmulas lógicas Utilizando los conectivos lógicos estudiados, se pueden combinar cualquier número finito de fórmulas lógicas para obtener el valor de verdad de otras expresiones más complejas. Tener en cuenta que el número de combinaciones de valores de verdad de una proposición, está supeditado al número de variables o proposiciones simples que intervienen. Para esto basta aplicar la fórmula: 2 n , donde “n” indica el número de variables que hay en la proposición compuesta.

15. Ejemplo: Construir la tabla de vedad de las siguientes expresiones lógicas: Solución: V F F F V F F V F F V F V F F V F V V F V F V V F F V V q p

16. F F F V V F F F F F F F V F V V V V F F V F F F V V V F V F V V V V V V V V V F F F V V F F F F F V F F V V F F V V F V V V V V F F V F V V V V V V F F V V V V r q p

17. Proposiciones equivalentes : Se dice que dos proposiciones son equivalentes, si tienen iguales valores de verdad. Ejemplo: Construyendo su tabla de verdad: Son equivalentes V V F F V V V F F F F V V V V V ~p ∨ q q p

18. Tautologías, contradicciones y contingencias: Una expresión proposicional se llama Tautología, si los valores de su tabla de verdad todos son verdaderos Una expresión proposicional se llama Contradicción, si los valores de su tabla de verdad, todos son falsos. Una expresión proposicional se llama Contingencia , si los valores de su tabla de verdad hay valores verdaderos y falsos

19. Determinar si el siguiente esquema es tautológico, consistente o contradictorio. V F V V V V V F F F F V V F F V V F V F F V V V F F V V F V F V V F F F V V V V q p

20. Dada las proposiciones : p: 18 es un número primo q: 4 es un número cuadrado perfecto. r: 13 es un número par Determinar el valor de verdad del siguiente esquema: V(p)= F V(q)= V V( r )= F Solución: = V V V V V V V

21. INFERENCIA LÓGICA Y CUANTIFICADORES La inferencia lógica, llamado también razonamiento lógico, es un par ordenado de la forma: Donde es un conjunto finito de proposiciones, llamadas premisas y ”q”, otra proposición, llamada conclusión. Es decir, si p 1 , p 2 , p 3 ….., p n , son proposiciones llamadas premisas y q la conclusión, entonces la implicación : Es una tautología Por lo tanto: Si la implicación es una tautología, entonces, se tiene un Argumento válido. Si la implicación es Falsa, entonces, se tiene una Falacia.

22. Ejemplo: Simbolizando, se tiene: P: El día está frío. q: El cielo está nublado. Simbolizando la inferencia Determinar la validez de la siguiente inferencia: “ El día está frío, entonces el cielo está nublado. El día está frío. Por lo tanto : El cielo está nublado” Solución:

23. Desarrollando la tabla de verdad de: Es una tautología, por lo tanto, la inferencia es Válida V F V F F F F V V V F F V F V F F F V F V V V V V V V V q p

24. Principales leyes lógicas o Tautologías:

25. Principales Leyes Lógicas

26. Equivalencias Notables

27. Equivalencias notables :

28. Principales leyes lógicas

29. Principales leyes lógicas

30. CUANTIFICADORES Función Proposicional : Es todo enunciado abierto, que tiene la propiedad de convertirse en una proposición al ser sustituido la variable “x” por una constante específica. Se les denota asi: P(x) ; q(x) ; etc. Ejemplo: Sea : p(x): x+5=12 ; donde si reemplazamos x por 3 , la expresión es falsa; si reemplazamos x por 7, la expresión es verdadera. Esto escribimos asi: P(3): 3+5=12 es falsa P(7): 7+5=12 es verdadera.

31. TIPOS DE CUANTIFICADORES 1.- Cuantificador Universal: Es toda función proposicional presedida por el Prefijo “Para Todo”, que está denotado por: Así por ejemplo: Se lee: “Para todo x perteneciente a los reales, x 2 es mayor o igual a cero” 2.- Cuantificador Existencial Es toda función proposicional presedida por el prefijo “Existe algún x”, que está denotado por :

32. Negación de los Cuantificadores: Dada una función proposicional , tal como : P(x), entonces si esta función proposicional está cuantificada y se niega,entonces, se cumple la siguiente igualdad: Dada una función proposicional, tal como : P(x), entonces, si esta función proposicional está cuantificada en forma existencial y se niega, entonces, se cumple la igualdad:

33. Circuitos lógicos Llamados también redes lógicas. Son como su nombre indica, redes que representan posiciones lógicas. Estas redes se presentan como redes en serie o como redes en paralelo /p /q

34. . P/ q/

35. Circuitos lógicos Describir simbólicamente el circuito 1. r y ~q están conectados en paralelo : r v ~q 2. P y (r y ~q) están conectados en serie: 3. q y ~r están conectados en serie: y Están conectados en paralelo, Luego se simboliza: p r ~q q ~r

36. Circuitos lógicos Determinar el circuito equivalente al circuito: ~p Solución El circuito se simboliza por: ~p q p q ~p

37. Circuitos lógicos Solución Simplificamos utilizando las leyes lógicas y las equivalencias notables. Asociativa Ley del tercio excluido , Idempotencia. Elemento neutro para la conjunción El circuito equivalente es: ~p q

38. CONJUNTO : Idea Intuitiva: La palabra conjunto sugiere de inmediato la idea de: Grupo Colección Selección Asociación Agregado , etc. NOTACION Para representar un conjunto se utilizan letras Mayúsculas, tales como A , B , C ....... LA TEORIA DE CONJUNTOS

39. ELEMENTO : Son los objetos que forman parte del conjunto la propiedad fundamental de un elemento es la pertenencia ; que se simboliza así  : Se lee : “ pertenece a ” A los elementos se les designa con letras minúsculas , tales como x , y , z etc. Si un elemento x forma parte del conjunto A, entonces, ese elemento pertenece a ese conjunto A así denotamos : x  A : Se lee: “ x pertenece a A” Si un elemento x no forma parte del conjunto A, entonces, ese elemento no pertenece a ese conjunto A. Así denotamos : x  A : Se lee: “ x no pertenece a A” Ejemplo : Sea A = {x , y , z} x  A y  A z  A m  A LA TEORIA DE CONJUNTOS

40. Determinación de un conjunto : Un conjunto se puede determinar: por extensión y por comprensión Por extensión : Nombrando uno a uno los elementos del conjunto Ejemplo: A = {m , n , p , q} Por Comprensión : Enunciando una propiedad o característica común a los elementos del conjunto. Ejemplo: A = {x  x es un número par } LA TEORIA DE CONJUNTOS

41. Conjuntos Especiales : Conjunto Unitario : Ejemplo: M = { x } ; N = { x  N  1 < x < 3 } Conjunto Nulo o Vacío : Denotado por  Ejemplo: P = { x  N  1 < x < 2 } =  Conjunto Finito Ejemplo: M = { x  x es número dígito par menor que 40 } Conjunto Infinito Ejemplo: N = { x  R  1 < x  5 } Conjunto Universal Constituido por todos los elementos de una determinada materia. El conjunto Universal no está definida en forma única, podemos elegir a nuestra conveniencia. Se denota por la letra U Ejemplo: Sea el universo U = { a , e , i , o , u } LA TEORIA DE CONJUNTOS

42. Diagrama de Veen - Euler : Consisten en representar a los conjuntos por medio de figuras geométricas planas y cerradas en cuyo interior se ubican los elementos. Ejemplo: A = {m , n , p } .m .n .p A LA TEORIA DE CONJUNTOS

43. Relaciones entre Conjuntos : LA INCLUSION Denotado por  se lee: está incluido o contenido . Se dice que un conjunto A está incluido en otro conjunto B, sí y solo sí , todos los elementos de A pertenece a B ; es decir : Ejemplo : Sea A = {2 , 3 , 5} y B = {1 , 2 , 3 , 4 , 5 , 6 } .1 .4 .6 La inclusión denotado por  da la posibilidad de que A y B tengan los mismos elementos .2 .3 .5 A B LA TEORIA DE CONJUNTOS

44. Subconjunto Propio o Parte Propia : Se dice que un conjunto A es subconjunto propio de o parte propia de B ; sí y solo si, todos los elementos de A pertenecen a B , existiendo elementos de B que no pertenecen a A ; se denota así: A  B se lee: A es subconjunto propio de B Nota : El conjunto nulo es subconjunto de todo conjunto .   A ;  A LA TEORIA DE CONJUNTOS

45. Propiedades de la Inclusión : Reflexiva : A  A ;  A Antisimétrica : Si A  B  B  A  A = B Transitiva : Para los conjuntos A , B y C Si A  B  B  C  A  C LA TEORIA DE CONJUNTOS

46. Igualdad de Conjuntos : A y B son iguales , cuando están formados por los mismos elementos. Y definimos así: Ejemplo: A={x , y } y B= { y , x } A = B LA TEORIA DE CONJUNTOS

47. Relaciones entre Conjuntos : Conjuntos Comparables .b .d .f Tienen algunos elementos en común. A={a , b , c , d} y B= { a , c , e , f} .a .c A B Conjuntos no comparables .e Conjuntos Disjuntos: Números pares Números impares A B No tienen ningún elemento en común LA TEORIA DE CONJUNTOS

48. Conjunto de conjuntos o familia de conjuntos : Es el conjunto que tiene como elementos a otros conjuntos. Ejemplo: A= { {1 , 2 } , { 0 } , { 3 } } LA TEORIA DE CONJUNTOS Conjunto Potencia Es el conjunto cuyos elementos son todos los subconjuntos de ese conjunto , incluyendo el mismo y el nulo. Dado un conjunto A ; el conjunto potencia de A, se denota por P(A) Luego : Ejemplo: Sea A = {a , b} P(A) = { {a } , { b } , { a , b } ,  }

49. Nota : Si A tiene “ n” elementos, el número de elementos de la P(A) es igual a 2 n elementos. LA TEORIA DE CONJUNTOS El conjunto potencia de A es una familia de conjuntos

50. El Conjunto de Números Naturales ( N ) N = { 1 , 2 , 3 ,4 , .................. } En este conjunto sólo se puede efectuar operaciones de adición y multiplicación sin restricciones. CONJUNTOS NUMERICOS El Conjunto de Números Enteros ( Z ) Son los números naturales precedidos por el signo - o + , incluyendo el cero. Z = { ............... – 3 , , - 2 , - 1 , 0 , 1 , 2 , 3 , .................. } Donde N  Z N Z

51. El Conjunto de Números Racionales ( Q ) Q = { x / x = ; a , b  Z ; b  0 } Es decir el conjunto Q resulta de dividir 2 números enteros , con el divisor diferente de cero . Y puede obtenerse. CONJUNTOS NUMERICOS N Z Q

52. Conjunto de Números Irracionales ( Q  ) Son aquellos números que no pueden expresarse en la forma ; b  0 a , b  Z , es decir que no presentan periodicidad en sus cifras decimales. CONJUNTOS NUMERICOS Q  = Conjunto de Números Reales ( R ) R = Q  Q  Nota: Existe una correspondencia biunívoca entre los elementos del conjunto de números reales y el conjunto de puntos de la recta . P i P 2 P 1 (x 1 ) (x 2 ) (x i ) -  + 

53. GRAFICA CONJUNTISTA R Q Z N Q’

54. El Conjunto de Números Complejos ( C ) Al resolver la ecuación : CONJUNTOS NUMERICOS i se llama unidad imaginaria Por lo tanto : Un número Complejo podemos escribir en la forma a + bi ; a ,b  R Luego : C = { a + bi  a , b  R ; i 2 = - 1 }

55. OPERACIONES ENTRE CONJUNTOS Unión o Reunión de Conjuntos Dado dos conjuntos A y B , se tiene : A  B = { x/ x  A  x  B } A B Si A y B son no comparables , entonces: A  B gráficamente es: Si A y B son comparables , entonces: A  B es: Si A y B son Disjuntos A  B es: B B A A

56. OPERACIONES ENTRE CONJUNTOS Propiedades de la Reunión de Conjuntos

57. OPERACIONES ENTRE CONJUNTOS Intersección de Conjuntos Dado dos conjuntos A y B , se tiene : A  B = { x/ x  A  x  B } A B Si A y B son no comparables , entonces: A  B gráficamente es: Si A y B son comparables , entonces: A  B es: Si A y B son Disjuntos A  B es: B B A A

58. OPERACIONES ENTRE CONJUNTOS Propiedades de la Intersección de Conjuntos

59. OPERACIONES ENTRE CONJUNTOS Diferencia de Conjuntos Dado dos conjuntos A y B , se tiene : A - B = { x/ x  A  x  B } Gráficamente , mediante el diagrama de Veen se tiene: A B Si A y B son no comparables , entonces: A - B es: Si A y B son comparables , entonces: A - B =  (No hay gráfico) Si A y B son Disjuntos A  - B es: B – A es: B A B A

60. OPERACIONES ENTRE CONJUNTOS Propiedades de la Diferencia de Conjuntos

61. OPERACIONES ENTRE CONJUNTOS Complemento de un Conjunto Dado el universo U y un conjunto A ; el complemento de A , denotado por A  O A c se define asi : A c = { x/ x  U  x  A } = U - A A c Gráficamente: A Si el conjunto referencial no es el conjunto universo, tal como B , donde A  B ; entonces el complemento de A con respecto a B , denotado por C B (A) Será : C B (A) = { x / x  B  x  A } = B - A U

62. OPERACIONES ENTRE CONJUNTOS Propiedades del Complemento

63. Diferencia Simétrica Dado dos conjuntos A y B ; la diferencia Simétrica , denotada por A  B se define así: A  B = (A – B ) U (B – A) B Gráficamente: A Ejemplo . Si A = { 2 , 3 , 5 } y B = { 0 , 1 , 2 , 3 , 8 , 9 } Hallar A  B Solución. Como A  B = (A – B )  (B – A) = { 5 }  { 0 , 1 , 8 , 9 } A  B = { 0 , 1 , 5 , 8 , 9 }

64. Propiedades de la Diferencia simétrica

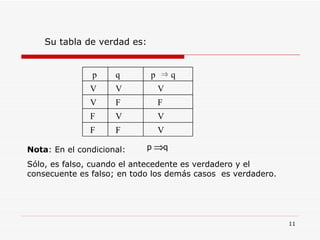
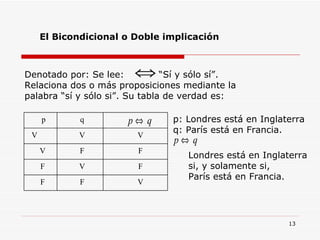
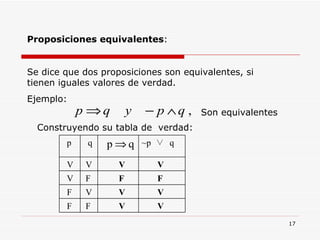
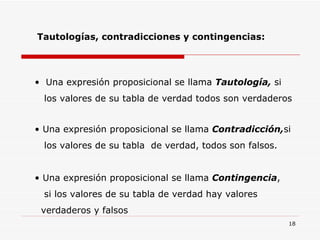
65. TEORIA DE CONJUNTOS Número de Elementos de un Conjunto Al número de elementos de un conjunto se le llama : Cardinal de un Conjunto y se denota así: Para un conjunto A se tiene n(A) ó Card (A Ejemplo . Si A = { a , e , i , o , u }  n(A ) = 5 ó n [ P(A) ] = 2 5 = 32

66. TEORIA DE CONJUNTOS Propiedades

67. TEORIA DE CONJUNTOS Para la gráfica de A , B y C se tiene: Las operaciones que representan las regiones: A B C R 1 R 4 R 5 R 7 R 2 R 6 R 3 R 8 U

68. TEORIA DE CONJUNTOS Para la gráfica de A , B y C se tiene: Las operaciones que representan las regiones: A B C R 1 R 4 R 5 R 7 R 2 R 6 R 3 R 8 U

69. TEORIA DE CONJUNTOS Ejemplo: Sean los conjuntos: A = { 1 , 2 , 3 , 4} ; B = { 0 , 2 , 5 , 6} y C = { 1 , 2 , 4 , 6 , 7 } con U ={ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } Hallar : Solución:

70. TEORIA DE CONJUNTOS Ejemplo: Si los conjuntos A y B tienen los siguientes datos: n(A  B) = 60 ; n(A – B) = 24 y n(B  A  ) = 20 Hallar: n(A) + n(B) Solución: Restando : (1) y (2) se tiene : n(B) = 36 Restando : (1) y (3) se tiene : n(A) = 40 Luego n(A) + n(B) = 40 + 36 = 76

71. TEORIA DE CONJUNTOS Ejemplo: Dado los conjuntos: A = { a , {a , b} } ; B = { a , b , { c } } ; C = A – B Hallar : a) P(A  C) b) P(A)  P(B) Solución:

72. Ejemplo: En una encuesta realizada en un centro hospitalario de Lima , conformado por 60 profesionales de la salud se tiene la siguiente información : 40 profesionales hablan inglés ; 28 hablan el francés , 16 hablan alemán ; 12 hablan el inglés y el francés 5 el inglés y el alemán , los tres idiomas sólo 2. Si el número de profesionales que hablan sólo el francés es igual al número de profesionales que hablan el francés y el alemán. ¿Cuántos hablan únicamente el francés? Solución: I F A 25 3 2 10 x 16-(3+2+x) 28-(10+2+x)

73. Solución: I F A 25 3 2 10 x 16-(3+2+x) 28-(10+2+x)