Este documento proporciona recomendaciones didácticas para docentes sobre cómo enseñar los capítulos de funciones y funciones lineales en un libro de matemáticas. Incluye sugerencias sobre cómo introducir cada tema, actividades para el aula, y ejercicios para reforzar los conceptos. También ofrece consejos específicos sobre cómo abordar diferentes secciones de cada capítulo.

















![Ejemplo 3
Dada la función g tal que x −→ 1/ x, encuentra las imágenes de 2, 1 ,
2 2 y −3.
Solución. Lo que debes hacer es determinar los valores f (2), f (1/2), f ( 2) y f (0):
1 1
f (2) = . f ( 2) = .
2 2
1
f (1/2) = 1 = 2. 1 1
f (−3) = =− .
2 −3 3
¿Cuál es la imagen de 0? Para calcularla, deberías poder calcular f (0):
1
f (0) = ;
0
sin embargo, esta división no existe; por tanto, f no se puede evaluar en 0, y 0 no tiene una
imagen respecto de la función f .
En el ejemplo 1, decimos que el número 0 no está en el dominio de la función f . En
general, cuando un número real a no tiene imagen respecto de una función f , decimos
que a no está en el dominio de la función, y que f (a) no existe.
El conjunto de todos los valores del conjunto de salida que tienen una ima-
gen en el conjunto de llegada de la función se llama dominio de la función
f , y se representa así: dom f .
Ejemplo 4
1
Encuentra el dominio de la función f : R −→ R tal que f ( x) = − .
(3 − x)2
Solución. Observa que el denominador es cero cuando x = 3. En x = 3, la operación
1
−
(3 − x)2
no existe. Por tanto, el dominio de la función f es ] − ∞, 3[ ∪ ]3, +∞[.
En el ejemplo 1, observa que el número 0 no tiene preimagen, pues no existe un
valor x de manera que 1 = 0. En este caso, decimos que 0 no está en el recorrido de la
x
función f .
El conjunto de todas las imágenes de una función f se llama recorrido de f ,
y se representa con rec f .
Ejemplo 5
1
Encuentra el recorrido de la función f : R −→ R tal que f ( x) = − .
(3 − x)2
Solución. Para determinar el recorrido, podemos observar que cualquier valor de salida
tiene la forma de una división, donde el numerador es siempre negativo y el denominador
es siempre positivo, sin importar el valor de x. El resultado de la división será siempre un
valor negativo. Simbólicamente:
(3 − x)2 > 0
19](https://image.slidesharecdn.com/matematica1cap1-120806104130-phpapp01/85/Matematica-1-cap1-18-320.jpg)
![para todo x ∈] − ∞, 3[∪]3, +∞[. Además,
1
−1 < 0 ⇒ − <0
(3 − x)2
para todo x ∈] − ∞, 3[∪]3, +∞[; es decir:
1
f ( x) = − < 0;
(3 − x)2
por tanto, el recorrido de la función f es el conjunto ] − ∞, 0[.
Ejemplo 6
2
Determina el dominio y el recorrido de la función h : R −→ R tal que h( x) = 3− x .
Solución. Podemos evaluar h( x) en cualquier valor de x, excepto en el caso cuando x = 3.
2
¿Por qué? (Observa que el denominador de la fracción 3− x es 0 cuando x = 3, y que no
podemos dividir por 0). Por tanto, el dom f es el conjunto constituido por todos los números
reales excepto el 3. Podemos representar el dominio de esta función de maneras diversas:
dom f = { x ∈ R : x = 3} = R − {3} =] − ∞, 3[ ∪ ]3, +∞[.
La determinación del recorrido es más difícil que la del dominio. En el ejemplo que te
ocupa, puedes hacerte una idea de cuál es el recorrido de la siguiente manera.
Recuerda que el recorrido es el conjunto de todos los números y = f ( x); entonces, estos
números y cumplen con la siguiente igualdad:
2
y=
3−x
siempre que x = 3. Ahora despeja x de esta igualdad; vas a obtener que
2
x = 3− .
y
El número representado por la expresión de la derecha de la igualdad existe para todos los
valores de y, excepto cuando y = 0 (¿por qué?). Entonces, el recorrido de f serán todos los
números reales distintos de 0. Esto lo puedes representar también de maneras diversas:
rec f = { y ∈ R : y = 0} = R − {0} =] − ∞, 0[ ∪ ]0, +∞[.
Ejemplo 7
Determina el dominio de la función g : R −→ R definida por g( x) = 2 x.
3
Solución. Podemos observar que la operación 2 x siempre se puede realizar con cualquier
3
número real x; por lo tanto, el dominio de la función g es el conjunto R.
Representaciones de una función
Las funciones pueden representarse de varias maneras; las más importantes son las
siguientes:
Numéricamente a través de una tabla.
20](https://image.slidesharecdn.com/matematica1cap1-120806104130-phpapp01/85/Matematica-1-cap1-19-320.jpg)




![Ejercicios
Preparación y repaso
En primer lugar, recuerda los diferentes tipos de intervalo:
1. [a, b] = { x : a ≤ x ≤ b}. 5. [a, +∞[ = { x : x ≥ a}.
2. ]a, b[ = { x : a < x < b}. 6. ]a, +∞[ = { x : x > a}.
3. [a, b[ = { x : a ≤ x < b}. 7. ]−∞, b] = { x : x ≤ b}.
4. ]a, b] = { x : a < x ≤ b}. 8. ]−∞.b[ = { x : x < b}.
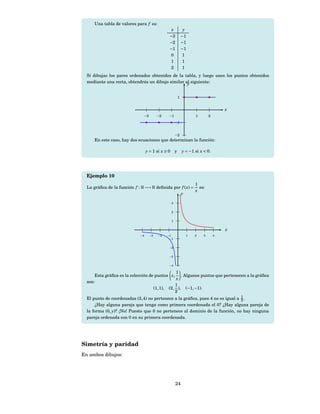
1. Expresa los siguientes conjuntos de nú- 3. En cada caso, traza la figura geométrica
meros reales como intervalos: cuyos vértices son:
(a) x∈R: 1 ≤ x≤5 .
2
(b) { x ∈ R : x < 0, 33}. (a) (−4, 0), (2, 0) y (0, −3).
(c) { x ∈ R : x < 1 y x > −2}.
2. En un sistema de ejes coordenados, ubi- (b) (−4, 2), (2, 2), (−4, −3) y (2, −3).
ca los puntos asociados con los siguien-
tes pares ordenados: (c) (−1, 0), (0, −1), (1, 0) y (0, 1).
(2, 1), (4, 3), (−7, 2),
(−3, −2), (11/5, −1), 6, −7 , 4. Sean los puntos (−3, 2), (−3, −4); halla
(−3, 5; −4, 7), (2;5, 5), (0, 3), dos puntos de tal manera que formen un
2, 3 , 2 3, − 5 , 0, 6 . cuadrado con los puntos dados.
Conceptos
1. Sea f una función; para cada caso, di si es verdadero o falso, y justifica tu respuesta.
(a) f (1) = 5 significa que la imagen de 5 por f es 1.
(b) f (0) = −6 significa que 0 es una preimagen de −6 por f .
(c) f ( 2) = 2 significa que 2 es una preimagen de 2.
2. Sean los conjuntos A = {a, b, c, d }, B = {1, 2, 3}. En los diagramas que se dan a continuación,
indica cuáles representan funciones de A en B. Si la respuesta es negativa, explica por
qué no es una función.
A −→ B A −→ B A −→ B A −→ B A −→ B A −→ B
a → 1 a 1 a → 1 a → 1 a → 1 a → 1
b → 2 b → 2 b → 2 b 2 b → 2 b 2
c → 3 c → 3 c 3 c 3 c 3 c 3
d d d d d d
(a) Los diagramas anteriores definen correspondencias entre los elementos de A y los de
B. Si C = {a, b, c} y D = {1, 3}, ¿cuáles de dichas correspondencias definen funciones
de C en D ?, ¿de C en B? y ¿de A en D ?
(b) Para cada una de las funciones encontradas en la parte a., determina la o las preimá-
genes de 1, de 2 y de 3.
(c) Determina todas las funciones que se pueden establecer de A en D y de D en D .
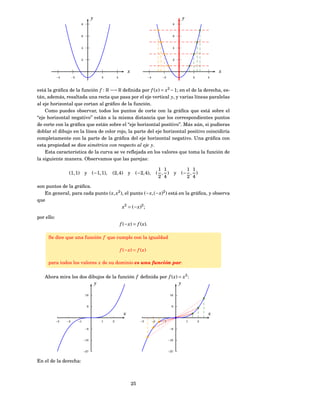
3. Una descripción verbal de una función está dada. Elabora una representación algebraica,
una gráfica y una tabular de dicha función.
(a) Para evaluar f ( x), a x se le multiplica por 3 y al resultado se le suma 4.
27](https://image.slidesharecdn.com/matematica1cap1-120806104130-phpapp01/85/Matematica-1-cap1-26-320.jpg)











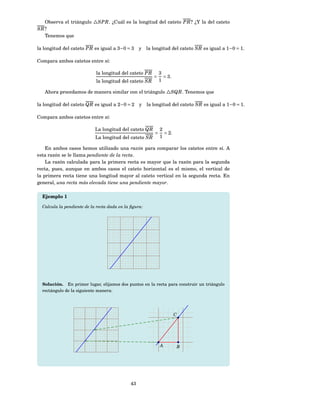
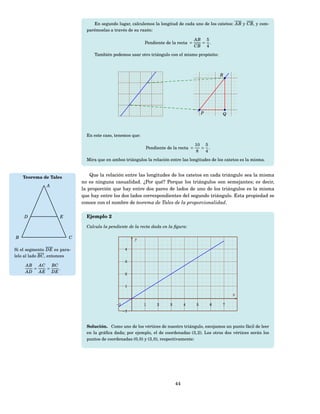
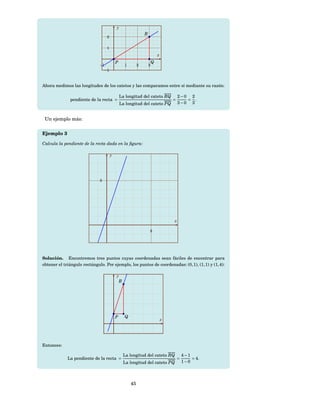
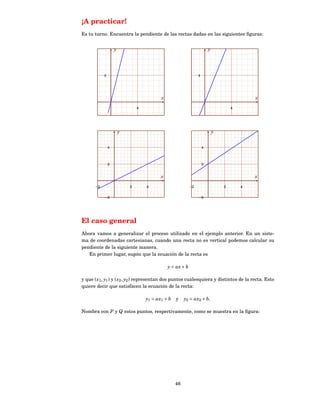


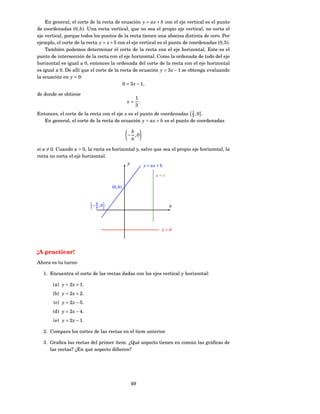






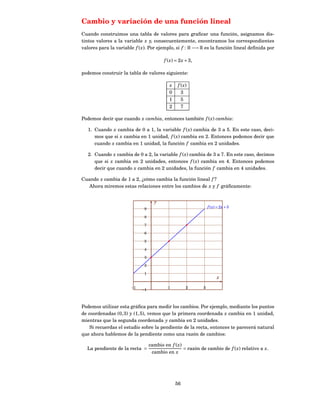



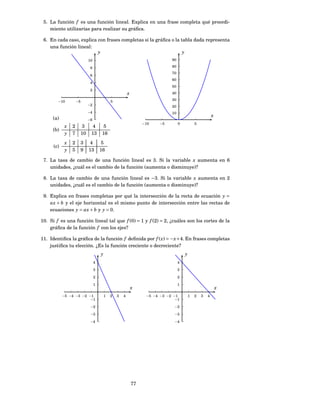
![Interpreta la variación de la función lineal g.
Si la variable x aumenta en 1 unidad, ¿cuánto cambia (aumenta o disminuye) la
función? ¿Y si disminuye en una unidad?
Si la variable x disminuye en 4 unidades, ¿cuánto cambia (aumenta o disminuye)
g( x)?
Solución. La tasa de cambio o variación relativa de la función lineal g es el coeficiente
de x en
g( x) = −3 x + 10.
Por lo tanto:
tasa de cambio de la función lineal g = −3.
Que la variación o tasa de cambio de g sea −3 quiere decir que cuando x cambia en 1
unidad, g( x) cambia en −3 unidades.
Por ejemplo, si x cambia de 4 a 5, entonces
g(5) − g(4) g(5) − g(4)
−3 = tasa de cambio de g = = .
5−4 1
Por lo tanto:
−3 = g(5) − g(4),
lo que significa que g(5) − g(4) es negativo; es decir, g(5) es menor que g(4). En otras
palabras, el cambio de g es una disminución.
En resumen, cuando x aumenta en una unidad, la función g disminuye en 3 unidades.
Supongamos que x aumenta en 1 unidad. Entonces, g( x) cambiará en 3 unidades, sin
importar el valor de x. Pero, ¿ g( x) aumentará o disminuirá en esas 3 unidades?
Para ello, calculemos la diferencia entre g( x + 1) y g( x):
g( x + 1) − g( x) = [−3( x + 1) + 10] − [−3 x + 10]
= [−3 x − 3 + 10] − [−3 x + 10]
= −3.
Como la diferencia es menor que 0, el aumento de x en una unidad significa una
disminución de g( x) en 3 unidades.
De manera similar:
g( x − 1) − g( x) = [−3( x − 1) + 10] − [−3 x + 10]
= [−3 x + 3 + 10] − [−3 x + 10]
= 3.
Como la diferencia es mayor que 0, g( x) aumenta en 3 unidades cuando x disminuye
en 1.
Por cada unidad de cambio en x, g( x) cambia en 3. Por lo tanto, si x cambia en 4
unidades, g( x) cambiará en 12 unidades.
De los ejemplos, podemos ver que:
la tasa de cambio de la función lineal f es positiva y, en este caso, un aumento en
x significa un aumento en f ( x), y una disminución en x, una disminución en f ( x);
la tasa de cambio de la función lineal g es negativa y, en este caso, un aumento
en x significa una disminución en g( x), y una disminución en x, un aumento en
f ( x).
60](https://image.slidesharecdn.com/matematica1cap1-120806104130-phpapp01/85/Matematica-1-cap1-59-320.jpg)
![Estos hechos también se cumplen en el caso general, lo que podemos verificar con faci-
lidad.
Consideremos una función lineal cualquiera
h : R −→ R
x −→ ax + b.
En primer lugar, supongamos que la tasa de cambio de h es positiva; es decir, suponga-
mos que a > 0. Esto quiere decir que si x cambia en una unidad, h( x) debe cambiar en
a unidades.
Ahora supongamos que x aumenta en una unidad; entonces: Variación de una
función lineal
h( x + 1) − h( x) = [a( x + 1) + b] − [ax + b] • Si la tasa de cambio de
= [ax + a + b] − [ax + b] una función lineal h es
positiva, al aumentar x,
= a > 0.
también aumenta f ( x); al
disminuir x, f ( x) también
Como esta diferencia es mayor que 0, h( x) aumentó a unidades.
disminuye.
Ahora, si x disminuye una unidad, tenemos que
• Si la tasa de cambio de
h( x − 1) − h( x) = [a( x − 1) + b] − [ax + b] una función lineal h es
negativa, al aumentar x,
= [ax − a + b] − [ax + b] disminuye f ( x); al dismi-
= − a < 0. nuir x, f ( x) aumenta.
Como esta diferencia es menor que 0, h( x) disminuyó a unidades.
De manera similar, puedes analizar el caso en que la tasa de cambio de h es nega-
tiva.
Ejemplo 14
Considera la función lineal h tal que la imagen de −2 es 1 y la imagen de 1 es −5. Si x
disminuye en 3 unidades, ¿en cuántas unidades cambia h( x)? ¿Aumenta o disminuye?
Solución. En primer lugar, tienes que averiguar la tasa de cambio de h. Para ello, vas a
encontrar dos puntos que estén en la recta que representa a la función lineal h.
Como 1 es la imagen de −2, y −5 la de 1, tenemos que
h(−2) = 1 y h(1) = −5.
Entonces los puntos de coordenadas
(−2, 1) y (1, −5)
están en la recta que representa a la función h. Por lo tanto, la tasa de cambio de h es la
pendiente de la recta:
1 − (−5)
tasa de cambio de h =
−2 − 1
6
= = −2.
−3
Como la tasa de cambio es −2, si x aumenta una unidad, h( x) disminuye 2; entonces, al
aumentar 3, disminuirá en 6 unidades.
61](https://image.slidesharecdn.com/matematica1cap1-120806104130-phpapp01/85/Matematica-1-cap1-60-320.jpg)