Este documento presenta información sobre el Bachillerato General Unificado 1o BGU, incluyendo una advertencia sobre el uso de un lenguaje inclusivo y no sexista. Contiene el índice de la unidad 3 sobre funciones cuadráticas y el espacio vectorial R2, con objetivos, contenidos y evaluaciones. Finalmente, proporciona datos sobre la edición y distribución del libro.





![Índice
Unidad 3
Función cuadrática y el espacio
vectorial en R2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
Análisis de la función cuadrática . . . . . . . . . . . . . . . . 122
Intervalos de la función cuadrática
donde es decreciente o creciente . . . . . . . . . . . . . . 124
Ecuación de segundo grado . . . . . . . . . . . . . . . . . . . . 128
Ecuaciones que se reducen a una
ecuación de segundo grado . . . . . . . . . . . . . . . . . . . . 134
Intersección gráfica de una recta y una
parábola como solución de un sistema
de dos ecuaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
Intersección gráfica de dos parábolas . . . . . . . . . . . . . 139
Sistemas de dos ecuaciones con dos
incógnitas en forma analítica . . . . . . . . . . . . . . . . . . 144
Modelos matemáticos con funciones
cuadráticas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
El conjunto R2
. Operaciones . . . . . . . . . . . . . . . . . . . 152
Interpretación geométrica de las
operaciones en R2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
Vectores colineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
El espacio euclídeo R2
. . . . . . . . . . . . . . . . . . . . . . . . . . 162
Longitud o norma de un vector . . . . . . . . . . . . . . . . 163
Distancia entre dos puntos . . . . . . . . . . . . . . . . . . . . . 164
Ortogonalidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
Ángulo entre dos vectores . . . . . . . . . . . . . . . . . . . . . . 165
Solucióndeproblemascotidianos . . . . . . . . . . . . . . . . . 168
Desafíos científicos . . . . . . . . . . . . . . . . . . . . . . . . . . 169
La matemática y las profesiones . . . . . . . . . . . . 169
TIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
Desafíos y proyectos matemáticos . . . . . . . . . . . 172
En síntesis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
Evaluación sumativa . . . . . . . . . . . . . . . . . . . . . . . . . 174
Unidad 4
Rectas en R2
y derivada de la función
cuadrática . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
Ecuación vectorial de la recta . . . . . . . . . . . . . . . . . . 178
Ecuación paramétrica de la recta . . . . . . . . . . . . . . . 180
Ecuación cartesiana de la recta . . . . . . . . . . . . . . . . . 184
Pendiente de la recta . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
Rectas paralelas y perpendiculares.
Intersección de rectas . . . . . . . . . . . . . . . . . . . . . . . . . . 186
Distancia entre dos números reales . . . . . . . . . . . . . 192
Noción intuitiva de límite . . . . . . . . . . . . . . . . . . . . . . 194
Significados de: x → 0, x → x0
+
y x → x0
–
. . . . . . . 194
Noción de límite de una función real . . . . . . . . . . 195
Cociente incremental. Noción de derivada . . . . . 198
Interpretación geométrica y física del
cociente incremental . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
Derivada de la función cuadrática . . . . . . . . . . . . . . 201
Velocidad y aceleración . . . . . . . . . . . . . . . . . . . . . . 204
Velocidad instantánea . . . . . . . . . . . . . . . . . . . . . . . . . . 205
Solucióndeproblemascotidianos . . . . . . . . . . . . . . . . 208
Desafíos científicos . . . . . . . . . . . . . . . . . . . . . . . . . . 209
La matemática y las profesiones . . . . . . . . . . . . 209
TIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
Desafíos y proyectos matemáticos . . . . . . . . . . . 212
En síntesis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213
Evaluación sumativa . . . . . . . . . . . . . . . . . . . . . . . . . 214
Unidad 5
Polinomios reales con coeficientes en R
y distacia de un punto a una recta . . . . . . . . . . . 216
Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217
Distancia de un punto a una recta . . . . . . . . . . . . . 218
Aplicaciones geométricas del producto
escalar en R2
. Teorema de Pitágoras . . . . . . . . . . . . 224
Ley del paralelogramo . . . . . . . . . . . . . . . . . . . . . . . . . . 225
El conjunto [R] de polinomios
con coeficientes reales . . . . . . . . . . . . . . . . . . . . . . . . . . 230
Operaciones con polinomios . . . . . . . . . . . . . . . . . . . 232
Adición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232
Resta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
Multiplicación de polinomios . . . . . . . . . . . . . . . . . . 236
Producto de números reales por polinomios . . 237
Solución de problemas cotidianos . . . . . . . . . . . . . . . 240
Desafíos científicos . . . . . . . . . . . . . . . . . . . . . . . . . 241
La matemática y las profesiones . . . . . . . . . . . . 241
TIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242
Desafíos y proyectos matemáticos . . . . . . . . . . 244
En síntesis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245
Evaluación sumativa . . . . . . . . . . . . . . . . . . . . . . . 246
Unidad 6
División de polinomios reales con
coeficientes en R. Probabilidad . . . . . . . . . . . . 248
Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249
División de polinomios. Teorema del residuo . . . . . 250
Aplicaciones de polinomios en la Informática . . 256
Conversión de binario a decimal y viceversa . . 257
Modelos matemáticos con funciones
polinomiales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260
Experimentos aleatorios . . . . . . . . . . . . . . . . . . . . . . . . 266
Operaciones con sucesos . . . . . . . . . . . . . . . . . . . . . . . 267
Operaciones con sucesos. Leyes
de De Morgan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
Unión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
Intersección. Conjuntos disjuntos . . . . . . . . . . . . . . 270
Diferencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
Complemento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
Factorial de un número natural.
Binomio de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274
Solucióndeproblemascotidianos . . . . . . . . . . . . . . . . 278
Desafíos científicos . . . . . . . . . . . . . . . . . . . . . . . . . 279
La matemática y las profesiones . . . . . . . . . . . . 279
TIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280
Desafíos y proyectos matemáticos . . . . . . . . . . 282
En síntesis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 283
Evaluación sumativa . . . . . . . . . . . . . . . . . . . . . . . 284
Respuestas a las evaluaciones sumativas . . . . . . . 286
Bibliografía y webgrafía . . . . . . . . . . . . . . . . . . . . 288
BC
1
BC
1
BC
3
BC
2
BC
2
BC
2
BC
1
BC
1
BC 2
BC 3
BC 1 Bloque Curricular 1: Álgebra y funciones
Bloque Curricular 2: Geometría y medida
Bloque Curricular 3: Estadística y Probabilidad](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-6-320.jpg)





![123
: subconjunto
≠: diferente de
: conjunto de números reales
Dom(f): dominio de f
Rec(f): recorrido de f
] ]
−∞, :
p intervalo cerrado a la
derecha
[ [
∞
, :
p intervalo cerrado a
izquierda
Simbología matemática
Ahora tratamos el caso a < 0.
Nuevamente, para todo x ,
2
0
2
+ ≥
x
b
a
2
≥ 0 y siendo a < 0, resulta
a
2
0
2
+ ≥
x
b
a
2
≤ 0. Luego, −
−
+ ≤
y
ac b
a
a x
b
a
4
4
=
2
0,
2 2
= a
2
0
2
+ ≥
x
b
a
2
≤ 0, de donde
4
4
.
2
≤
−
y
ac b
a
En este caso, el recorrido de f es el conjunto = ,
4
4
.
2
( ) −∞
−
Rec f
ac b
a
Rec f
( )=
,
4ac b2
4a
, si a<0,
4ac b2
4a
, , si a>0.
.
En conclusión, Rec f
( )=
,
4ac b2
4a
, si a<0,
4ac b2
4a
, , si a>0.
En un capítulo posterior se estudiarán las cónicas. Allí se verá que la
gráfica de la función cuadrática representa a una parábola que se abre
hacia arriba, si a > 0, y hacia abajo, si a < 0. El punto
2
,
4
4
2
−
−
b
a
ac b
a
se llama vértice de la parábola.
Máximos y mínimos de las funciones cuadráticas
Mínimo de la función cuadrática
Sea a > 0. Puesto que para todo x , ( )
4
4
,
2
≥
−
f x
ac b
a
el número
real =
4
4
2
−
m
ac b
a
se llama mínimo global de la función cuadrática.
Escribiremos:
=
−
= ∈
4
4
mín ( ),
2
m
ac b
a
f x
x
mín f (x),
que se lee "m es el mínimo de la función f en todo ".
Máximo de la función cuadrática
Sea a < 0. Como para todo x , ( )
4
4
,
2
≤
−
f x
ac b
a
el número real
=
4
4
2
−
M
ac b
a
se llama máximo global de la función cuadrática.
Escribiremos:
−
∈
=
4
4
=máx ( ),
2
M
ac b
a
f x
x
máx f (x),
que se lee “M es el máximo de la función f en todo ".
Nótese que: f
2
=
4
4
=
,si >0,
,si <0.
2
−
−
f
b
a
ac b
a
m a
M a
2
=
4
4
=
,si >0,
,si <0.
2
−
−
f
b
a
ac b
a
m a
M a
2
=
4
4
=
,si >0,
,si <0.
2
−
−
f
b
a
ac b
a
m a
M a
x
x
Recuerda que…
• El mínimo global de la
función cuadrática es el mínimo
de la función que se representa
como:
m = mín f (x)
≤ ∀ ∈
∈ f x
m f x x
x
mín ( )
( ), .
• Si a < 0, y la función cuadrá-
tica f no tiene mínimo global,
escribiremos:
mín f (x) = – ∞, o simple
mente,
mín f (x) no existe.
• El máximo global de la fun-
ción cuadrática es el máximo
de la función que se representa
como:
M = máx f (x)
≤ ∀ ∈
∈
máx ( )
( ) ,
f x
f x M x
x
.
• Si a 0, y la función cuadrá-
tica f no tiene máximo global,
escribiremos:
máx f (x) = ∞, o simple
mente,
máx f (x) no existe.
x
x
x
x
x
x](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-12-320.jpg)

![125
x
1
2
0
decrece crece
p Figura 3.4.
p Figura 3.5.
1 2 3 4
–1
–2
–3
–4
y
x
0
y = –(x–2)²
Interdisciplinariedad
Matemática con la
vida cotidiana
Las funciones cuadráticas son
ampliamente usadas en la cien-
cia, los negocios y la ingeniería.
La parábola, puede describir
trayectorias de chorros de agua
en una fuente y el botear de
una pelota o definir la curva-
tura en estructuras como reflec-
tores y antenas parabólicas que
forman, respectivamente, los
faros de los carros y la base de
los platos satelitales. ¿Qué otro
tipo de aplicaciones tienen las
funciones cuadráticas?
Shutterstock,
(2020).
368766932
Entonces ≤ −
x x
1
2
.
1 2 Sumando
1
2
en la desigualdad, se obtiene
1
2
1
2
0,
1 2
+ + ≤
x x de donde x1 +
1
2
2
x2 +
1
2
2
0 , y
sumando
3
4
en esta última desigualdad, se deduce
x1 +
1
2
2
+
3
4
x2 +
1
2
2
+
3
4
3
4
, es decir que ( ) ( )
3
4
.
1 2 ≥
f x f x
De modo similar, se muestra que si x1 ,x2
1
2
, , tal que x1
x2
,
entonces
3
4
( ) ( ).
1 2
f x f x La prueba se propone como ejercicio.
En la gráfica siguiente se interpretan estos dos resultados (Figura 3.4.).
2. Consideremos la función g, definida como
− + − ∀ ∈
( )= 4 4, .
2
g x x x x
Puesto que
− + − − − + − − ∀ ∈
( )= 4 4 = ( 4 4 )= ( 2) , ,
2 2 2
g x x x x x x x x y
tomando en consideración que ( 2) 0, ,
2
x x
− ≥ ∀ ∈ resulta
( ) 0, ,
g x x
≤ ∀ ∈ es decir que el recorrido de g es el conjunto
Rec g − ∞
( )=] , 0]. El dominio de g es obviamente el conjunto .
Calculemos algunos valores de la función g.
(2)= (2 2) =0, (1)= (1 2) = 1,
2 2
− − − − −
g g − − −
g(3) = (3 2) = 1.
2
En la Figura 3.5. se muestra la gráfica de la función g.
Esta es una parábola que se abre hacia abajo,
− − ∀ ∈
( ) = ( 2) ,
2
g x x x , y su vértice es el punto (2, 0).
x
Se tiene 0 = g(2) = máx g(x).
Esta función es estrictamente creciente en el intervalo ]–∞, 2] y estric-
tamente decreciente sobre el intervalo [2, ∞[ .
Probemos que es estrictamente creciente en el intervalo ]–∞, 2].
Sean x1
, x2
]–∞, 2], tal que x1
x2
≤ 2. Sumando –2 en la desigual-
dad, obtenemos x1
–2 x2
–2 ≤ 0, de donde x x
− −
( 2) ( 2)
1
2
2
2
,
y multiplicando por –1, en esta última desigualdad, se deduce
x x
− − − −
( 2) ( 2) ,
1
2
2
2
es decir que ( ) ( ).
1 2
g x g x
Así, ∈ −∞
, ] ,2], ( ) ( ),
1 2 1 2 1 2
x x x x g x g x
⇒
∈ −∞
, ] ,2], ( ) ( ),
1 2 1 2 1 2
x x x x g x g x lo que muestra que g es
creciente en el conjunto I = ]–∞, 2]. En forma similar, se prueba que g
es decreciente en el conjunto I = [2, ∞[.
p Antena parabólica satelital.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-14-320.jpg)





![131
Recuerda que…
• Hemos visto que la
función f se escribe como
f(x)= a x2
+
b
a
x+
c
a
, x .
Además, la ecuación en ,
+ +
( ) = 0 = 0
2
f x ax bx c
⇔
+ +
( )= 0 = 0
2
f x ax bx c ,
tiene solución en si y
solo si el discriminante
= − ≥
4 0,
2
d b ac en cuyo
caso sus raíces reales son:
=
− − −
=
− + −
4
2
,
4
2
.
1
2
2
2
x
b b ac
a
x
b b ac
a
• En conclusión, dada la función
cuadrática f, definida como
= + + ∀ ∈
( ) , ,
2
f x ax bx c x
con a, b, c , a ≠ 0, las raíces
reales x1
, x2
de la ecuación
ax2
+ bx + c = 0 satisfacen las
relaciones + = −
1 2
x x
b
a
y
⋅ =
1 2
x x
c
a
.
Además, la función f se
factoriza en la forma
( ) = ( )( ), .
1 2
f x a x x x x x
− − ∈
Obsérvese la equivalencia
− −
( ) = 0 ( )( )= 0
1 2
f x a x x x x
− −
( )= 0 ( )( )= 0
1 2
f x a x x x x
y siendo a ≠ 0, se deduce
x x1 =0,o
x x2 =0
x = x1, o
x = x2
Este último resultado muestra
que la ecuación de segundo
grado tiene, a lo más, dos raíces
reales y distintas.
.
2.
Si es posible, factoriza la función f definida por
+ + ∀ ∈
( )= 2 2, .
2
f x x x x
En primer lugar, estudiemos la existencia de raíces reales de la
ecuación x2
+ 2x + 2 = 0. Para el efecto, calculamos el discrimi-
nante d de dicha ecuación. Tenemos a = 1, b = 2, c = 2, luego,
d = b2
– 4ac = 4 – 8 = –4 0.
Laecuaciónx2
+2x+2=0 notieneraícesreales,porlotanto,lafunción
realfnopuedefactorizarseenlaforma ( ) =( )( ), ,
1 2
f x x x x x x
− − ∈
con x1
, x2
.
Obsérvese que
( ) = 2 2 =( 1) 1 1, ,
2 2
f x x x x x
+ + + + ≥ ∀ ∈
x
con lo que mín f (x) = 1.
Propiedades de la raíces. Factorización de funciones cuadráticas
Consideremos la función cuadrática f, dada por
+ + ∈
( ) = , ,
2
f x ax bx c x donde a, b, c con a ≠ 0.
Calculemos x1
+ x2
. Tenemos:
=
4
2
4
2
=
4 4
2
= .
1 2
2 2 2 2
x x
b b ac
a
b b ac
a
b b ac b b ac
a
b
a
+
− − −
+
− + − − − − − + −
−
4 4
2
=
4 4
2
= .
2 2 2 2
b ac
a
b b ac
a
b b ac b b ac
a
b
a
−
+
− + − − − − − + −
−
Luego, la suma de las raíces x1
, x2
de la ecuación de segundo grado
satisfacen la relación = .
1 2
x x
b
a
+ −
Calculemos x1
∙ x2
:
x x
b b ac
a
b b ac
a
b ac b b ac b
a
c
a
=
4
2
4
2
=
4 4
4
.
1 2
2 2
2 2
2
( )( )
⋅
− − −
⋅
− + −
−
− + − −
=
ac
a
b b ac
a
b ac b b ac b
a
c
a
4 4
2
=
4 4
4
.
2 2
2 2
2
( )( )
−
⋅
− + −
−
− + − −
=
Por lo tanto, el producto de las raíces x1
, x2
de la ecuación de segundo
grado satisface la relación = .
1 2
x x
c
a
⋅ En consecuencia, la función f se
escribe como sigue:
=a x(x x1)+x2 ( x+x1)
[ ]=a x(x x1) x2 (x+x1)
[ ]=a(x x1)(x+x2).
f(x)=a x2
+
b
a
x+
c
a
=a x2
(x1 +x2)x+x1x2 =a x2
x1x+x2x+x1x2
Nótese que hemos utilizado la propiedad distributiva de los números
reales y la identidad ( ) = ( ), , , .
a b c a b c a b c
− + − − ∀ ∈ Así, la función
cuadrática f o polinomio de grado 2 con coeficientes en se escribe
en la forma ( ) = ( )( ), .
1 2
f x a x x x x x
− + ∈ Es decir que la función f
se ha factorizado.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-20-320.jpg)


















![151
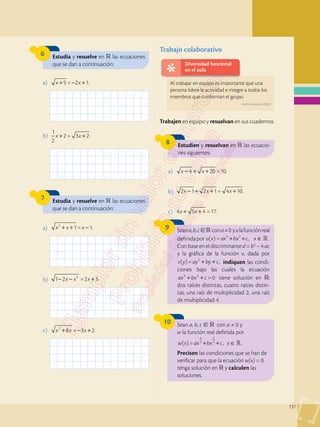
3 Un equipo mecánico cuesta v dólares,
v = 20 p + r 500, p, r +
, 0 ≤ r 20.
El comprador dispone solo billetes de
veinte dólares. La cajera tiene únicamen-
te billetes de cinco dólares y tres billetes
de un dólar. ¿Es posible disponer de m
billetes de veinte dólares para el pago y
n billetes de cinco dólares para el vuelto
que arregle la compra del equipo? Mues-
tra las soluciones gráficamente.
a) Calculen las constantes t0
, a, α1
.
b) Calculen las constantes a1
, v0
, β1
, β2
, β3
y t1
.
Para el efecto, asuman que ( )= 400
2 0
s t m
y v t v
= .
0 0
( )
c) Escriban en forma explícita las funciones
S y V.
d) Muestren que V es creciente en [0, t0
]
y decreciente en [t0
, t1
]
Comentario. Se debe resolver una ecua-
ción de la forma 20m – 5n –3 = v, con
m, n Z+
, conocida como ecuación dio-
fantina (en honor al matemático Diofante).
En este problema se requieren conocimien-
tos del espacio vectorial 2
y subespacios
de 2,
de la ecuación vectorial y cartesiana
de una recta, la representación gráfica, así
como de la divisibilidad en Z. Es obvio que
se requieren propiedades algebraicas y de
orden en el conjunto .
Diversidad funcional
en el aula
Es importante que haya tiempo suficiente para
que realicen su trabajo personas que puedan
tener dificultades en su motricidad, deben tener
paciencia e incorporarlos al trabajo.
Trabajo colaborativo
4 Resuelvan. La distancia entre dos paradas
de buses es 800 m. Una unidad de trans-
porte público debe recorrer esta distancia
siguiendo dos criterios: acelerar en una
primera etapa y, luego, desacelerar.
Se buscan dos funciones S y V de las for-
mas siguientes:
s t
t si t t
t t t t s t t t t
α
β β β
( ) ( )
( )
( )
≤ ≤
− + − + ≤
=
, 0 ,
= ,
1
2
0
1 0 2 0
2
3 2 0 1
v t
at si t t
a t t v si t t
=
, 0 ,
, ,
0
1 0 0 0
( )
( )
≤ ≤
− +
v t
at si t t
a t t v si t t
=
, 0 ,
, ,
0
1 0 0 0
( )
( )
≤ ≤
− +
donde: v v t
m
s
0 =0, =10
0
( )
( ) y
s t m s t m
400 , 800
0 1
( ) ( )
= = , cuando
v(t1
) = 0.
Trabajen en equipo, indaguen y resuelvan.
m
s
t0 t1
400
800
0
s = α1t²
s = s2(t)
s
(m)
10
v
m
s
v1 = at
t0 t1
v1 = a1 (t–t0)–v0
t(s)
0
Archivo editorial, (2020).](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-40-320.jpg)





![157
5
6
7
Sea U2
. Prueba que –(–U) = U, y,
–(–(–U)) = –U.
Sean U, V, W2
. Demuestra las
siguientes igualdades:
Sea U 2
. Prueba que el opuesto
aditivo de U es único. Para el efecto,
asume que existe otro opuesto
distinto al opuesto de U y obtén una
contradicción.
8 Sean ( , ),
1 1 1
=
A a b ( , ),
2 2 2
=
A a b
( , ),
3 3 3
=
A a b ( , )
4 4 4
=
A a b cuatro
elementos de 2
. Demuestren que se
tienen las siguientes igualdades:
[ ( )]
1 2 3 4
+ + + =
A A A A
[( ) ]
1 2 3 4
+ + + =
A A A A ( + )+( + )
1 2 3 4
A A A A
( , ).
1 2 3 4 1 2 3 4
+ + + + + +
a a a a b b b b
En vista de este resultado, se escribe
simplemente + + + ,
1 2 3 4
A A A A y
( , ).
1 2 3 4 1 2 3 4 1 2 3 4
+ + + = + + + + + +
A A A A a a a a b b b b
( , ).
1 2 3 4 1 2 3 4 1 2 3 4
+ + + = + + + + + +
A A A A a a a a b b b b
9 Resuelvan en el cuaderno.
Sea N el conjunto de los números
naturales. Se denota con N2
al producto
cartesiano N × N. Esto es, N2
= {(m, n)|
m, n N}. En N2
, se define la igualdad
y la operación adición “” como sigue:
Igualdad. Sean (m, n), (p, q) N2
.
Entonces (m, n) = (p, q) m = p^n = q.
Adición “”. Sean (m, n), (p, q) N2
.
Se define (m, n) + (p, q) = (m + p, n + q),
donde + es la operación adición en N.
Prueben que la operación adición
“” en N2
satisface las siguientes
propiedades: clausurativa, conmutativa,
asociativa, existencia de elemento
neutro. (N2
, ) no es grupo. La
operación “” en N2
es la operación “+”
en 2
, restringida al conjunto N2
2
.
10 Dados los vectores
( 3,1); (2, 2); (0,3)
= − = − =
A B C , obten-
gan el vector v u
λ λ λ λ
( ) ( )
= = =
3,1 3 ,
que se define en cada caso.
a) ( ) .
− − = − + = + −
U V W U V W U W V
b) ( ) .
− + + = − − −
U V W U V W
c) ( ( )) ( ).
− − − = − + − = − +
U V W U V W V U W
a) 2 .
= + +
u A B C b) 5
1
3
.
= − + +
u A B C
c) 3 10 20 .
= − − −
u A B C
d) 10 8 4 .
= − +
u A B C
Diversidad funcional
en el aula
Si una persona tiene discapacidad auditiva
o dificultades para escuchar, es necesario encon-
trar otras formas de comunicación, por ejemplo
escribir el mensaje, eso puede ayudar en las
actividades de esta sección.
Trabajo colaborativo
Trabajen en equipo y resuelvan en sus cuadernos.
Archivo editorial, (2020).](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-46-320.jpg)







![165
α β
γ
0
C
A
x
y
v
u √3
2
, 0
B =
En la Figura 3.26. se muestran el vector
A , el vector
B S y la recta S.
Obsérvese que el símbolo ha sido dibujado para indicar que el
vector
A y el conjunto S forman un ángulo recto en el punto O.
Ángulo entre dos vectores
Definición
Sean A B
, 2
∈ nonulos.Elángulo θ π
[ ]
∈ 0, entrelosvectores
A y
B
se define como θ =
⋅
A B
A B
cos( ) .
De la definición del ángulo entre los vectores
A y
B, se sigue que
⊥ ⋅
A B A B = 0
⇔
⊥ ⋅
A B A B = 0, con lo cual θ
cos( ) = 0, de donde θ
π
=
2
.
Por este motivo, dos vectores perpendiculares u ortogonales forman
un ángulo recto.
Ejercicio resuelto
Los vértices de un triángulo son los puntos ( )
= 0,0 ,
A ( )
= ,0 ,
3
2
B
( )
= , .
3
2
1
2
C Calcular las medidas de los ángulos interiores del triángu-
lo. En la Figura 3.27. se muestran los ángulos interiores del triángulo T.
Cálculo de α. Sean
,
u v los vectores que se definen a continuación:
u =B A=
3
2
,0 0,0
( )=
3
2
,0 ,
v =C A=
3
2
,
1
2
0,0
( )=
3
2
,
1
2
.
u = A B=
3
2
,0 , v =C B= 0,
1
2
.
Entonces, ⋅
u v =
3
4
,
u =
3
2
, v =1.
Luego,
α α
π
=
⋅
= = =
cos( )
3
4
3
2
3
2 6
.
u v
u v
Cálculo de β. Para el efecto, se definen los vectores
,
u v , como sigue:
u =B A=
3
2
,0 0,0
( )=
3
2
,0 ,
v =C A=
3
2
,
1
2
0,0
( )=
3
2
,
1
2
.
u = A B=
3
2
,0 , v =C B= 0,
1
2
.
Calculamos sus longitudes y el producto, y obtenemos
u =
3
2
, =
v
1
2
, u v = 0.
⋅
Por lo tanto,
,
u v son ortogonales y, en consecuencia,
β
⋅
→β
π
u v
u v
cos( )= = 0 =
2
.
⇒
β
⋅
→β
π
u v
u v
cos( )= = 0 =
2
.
Así,
6 2 3
,
γ π α β π
π π π
= − − = − − = .
Recuerda que…
El teorema de Pitágoras
enuncia que, en todo triángulo
rectángulo, la hipotenusa al
cuadrado es igual a la suma de
los cuadrados de los catetos.
Este resultado es extendido al
espacio euclídeo 2
.
Teorema de Pitágoras
Sean A B
, 2
∈ .
Entonces, ⊥
A B si y solo si
+ = +
A B A B .
2 2 2
.
Recuerda que…
Ley de cosenos
Sean A B
, 2
∈ no nulos y
[ ]
θ∈ π
0, el ángulo que for-
man los vectores A B
y .
Como ⋅ θ
A B A B
= cos ,
resulta que
− + − θ
B A B A A B
= 2 cos .
2 2 2
–1 1
x
1
0
y
2 B
A
S
p Figura 3.26
p Figura 3.27.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-54-320.jpg)












![178
Ecuación vectorial de la recta
DCCD: M.5.2.9. Escribir y reconocer la ecuación vectorial y paramétrica de una recta a partir de un punto de la recta y un vector dirección, o a partir
de dos puntos de la recta.
Definición. Sean 0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
un sistema de referencia ortogonal del
plano,
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
fijos con
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
. El conjunto L definido como
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
se llama recta que pasa por
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
y es paralela
a
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
. El vector
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
se llama vector director o vector generador de la
recta de L.
La ecuación
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
, se llama ecuación vectorial de la
recta L.
De la definición se sigue que L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
. Además, cada elemento de la
recta L es de la forma u + tv
para algún
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a
(
{
x t
( )= a,t
( )t .
, más aún, se tiene la
siguiente equivalencia:
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )=(
{
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
tal que .
su negación se escribe:
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
(
{
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
Los vectores
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
y
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
con t R, t 0, son colineales. En la Figura 4.1.
se muestran los vectores
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
v 0.
y el conjunto L; recta que pasa por
los extremos de
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
y
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
.
Ejercicio resuelto
Sean
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
y
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
. El subconjunto L de 2
queda definido
como sigue,
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
2
, y se denomina recta L
que pasa por (–2, 0) y es paralela al vector
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )=(
{
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
. Esta es una recta paralela
al eje Y.
Una ecuación vectorial de esta recta es:
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
, tR. Por ejemplo, para t = 0, se
tiene
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
, para t = 1, ( ) ( )
=
x
1, 1 –2,1
, para t = –2,
x
(–2) = (–2, –2). En la Figura 4.2. se muestra la recta L.
De manera más general, sea
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
= (a, 0) con a R,
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x
{
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
v 0.
L= u+tv t
{ }
x t
( )=u+tvt .
.
La recta que pasa por
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
y es paralela a
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
es el conjunto L definido como
{ } { }
( ) ( ) ( ) ( ) ( )
= = + ∈ = = ∈
L x t a t t x t a t t
,0 0,1 ,
Una ecuación vectorial de esta recta está dada como x t
( )= a,t
( )t .
, t R.
Otra ecuación vectorial de la recta L está definida como sigue:
x t
( )= a,t
( )t .
(a, –2) + t(0, –1), t R.
Esta recta es paralela al eje Y. En la Figura 4.3. se muestra esta recta L.
Segmentos de recta
Sean
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
v 0.
L= u+tv t
{ }
R2
con
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
≠ 0. La recta L que pasa por
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
v 0.
L= u+tv t
{ }
y es paralela a
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
es el conjunto
L 2
t
x L t
x =u+tv
x L t
x u+tv
v
tv
u,v ,tv ,x
u = 2,0
( )yv = j = 0,1
( )
L= x t
( )= 2,0
( )+t 0,1
( )t
{ }
j
x t
( )= 2,0
( )+t 0,1
( )= 2,t
( )
t
x 0
( )= 2,0
( )=u
t =1,x 1
( )= 2,1
( )
t = 2,x 2
( )= 2,2
( )
u = a,0
( )
a
a 0, v = j = 0,1
( )
L= x t
( )= a,0
( )+t 0,1
( )t
{ }= x t
( )= a,t
( )t
{ }.
x t
( )= a,t
( )t .
x t
( )= a, 2
( )+t 0,–1
( )t .
u ,v 2
v 0.
L= u+tv t
{ }
x t
( )=u+tvt .
. La ecuación vectorial viene defi-
nida como ( )= +
∈
x t u tv
t
, t R.
Saberes previos
¿Qué es un sistema de
referencia ortogonal del plano?
0
v
v
u
x
u
u
t
L
y
x x
y
j j
u
j
u
x(1)
L
x(–2)
–2 –1
–1
–2
0
j
+ t
y L
a x
0
u
v
v
v
y
x
W
x1
x0
L = u + W
[A, B]
(x, y)
b
y0
x0 a x
y
L
0
0
A
B 1 2 3 4 5
1
2
3
4
5
6
7
0
–1
–2
–3
A
B
x
y
[A, B]
p Figura 4.1.
u
x
y
j j
x(1)
L
x(–2)
–2 –1
–1
–2
0
1 2 3 4 5
1
2
3
4
5
6
7
0
–1
–2
–3
A
B
x
y
[A, B]
p Figura 4.2.
0
v
v
u
x
u
u
t
L
y
x x
y
j j
u
j
u
x(1)
L
x(–2)
–2 –1
–1
–2
0
j
+ t
y L
a x
0
u
v
y
x
W
x1
x0
L = u + W
[A, B]
0
A
B 1 2 3 4 5
1
2
3
4
5
6
7
0
–1
–2
–3
A
B
x
y
[A, B]
p Figura 4.3.
.
Recuerda la definición
Dados dos puntos
distintos A, B cualesquiera en
el plano, existe una y solo una
recta L que los contiene.
.
Desequilibrio cognitivo
¿Es posible determinar
las características cinemáticas de
una partícula en movimiento con
el uso de las ecuaciones vectoria-
les y paramétricas de la recta?](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-67-320.jpg)
![179
Sea t0
, t1
R, tal que t0
t1
. Ponemos
( )
( )
= = +
= = +
x x t u t v
x x t u t v
,
.
o
0 0
1
1 1
( )
( )
= = +
= = +
x x t u t v
x x t u t v
,
.
o
0 0
1 1 1
Al vector le asociamos el punto A y al vector , el punto B.
El segmento de recta de extremos los puntos A, B denotamos con
[A, B]. o también y es subconjunto de L definido como
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L= 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
La ecuación vectorial del segmento de recta [A, B] está definido
como:
( )
[ ]
= +
∈
x t u tv
t t t
, .
0 1
( )
[ ]
= +
∈
x t u tv
t t t
,
0 1
En la Figura 4.4. se muestran los vectores
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
,
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
, la recta L y el segmen-
to de recta [A, B].
Ejercicios resueltos
1) Sean
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L = 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
La ecuación
vectorial de la recta L está definida como
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L= 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
, t R.
Para
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L = 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
Para
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L = 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
A los vectores
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L= 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
les asociamos los puntos A y B. El segmento de
recta [A, B] está definido como el subconjunto de L siguiente:
AB= x0 ,x1
[ ]= A,B
[ ]= u+tv t t0 ,t1
[ ]
{ }.
x t
( )=u+tv
t t0 ,t1
[ ].
A,B
[ ].
L= 3,1
( )+t –1, 2
( )t
{ }, t0 =–2 y t1 =3.
x t
( )= 3,1
( )+t –1,2
( )t .
t0 =–2, x0 = x –2
( )= 3,1
( )–2 –1, 2
( )= 5, –3
( ).
t1 =3,x1
= x 3
( )= 3,1
( )+3 –1, 2
( )= 0, 7
( ).
x0 , x1
A,B
[ ]= 3,1
( )+t –1,2
( )t –2,3
[ ]
{ }.
x t
( )= 3,1
( )+t –1,2
( )t –2,3
[ ].
La ecuación vectorial de este segmento de recta está definido como
( ) ( ) ( )
[ ]
= +
∈
x t t
t
3,1 –1,2
–2,3 .
( )
[ ]
= +
∈
x t u tv
t t t
,
0 1
,
En la Figura 4.5. se muestra el segmento [A, B].
2) Sean
u,v 2
u v
u,v
x t
( )=u+t v –u
( ), t 0,1
[ ].
x 0
( )= uyx 1
( )=v , luego u,v
[ ]= u+t v –u
( )| t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
x 0
( )= –2,–3
( )=u
t =1,x = 4,2
( )=v ,
u
v
u,v
[ ]= –2,–3
( )+t 6,5
( )| t 0,1
[ ]
{ }
x t
( )= –2,–3
( )+ 6,5
( ), t 0,1
[ ]
obtén la ecuación vectorial de la
recta que pasa por estos puntos.
u,v 2
u v
u,v
x t
( )=u+t v –u
( ), t 0,1
[ ].
x 0
( )= uyx 1
( )=v , luego u,v
[ ]= u+t v –u
( )| t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
x 0
( )= –2,–3
( )=u
t =1,x = 4,2
( )=v ,
u
v
u,v
[ ]= –2,–3
( )+t 6,5
( )| t 0,1
[ ]
{ }
x t
( )= –2,–3
( )+ 6,5
( ), t 0,1
[ ]
, t R.
Para t = 0, se tiene
u,v 2
u v
u,v
x t
( )=u+t v –u
( )t 0,1
[ ].
x 0
( )=uyx 1
( )=v ,luego u,v
[ ]= u+t v –u
( )/t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
x 0
( )= –2,–3
( )=u
t =1, x = 4,2
( )=v ,
u
v
u,v
[ ]= –2,–3
( )+t 6,5
( )/t 0,1
[ ]
{ }
y para
u,v 2
u v
u,v
x t
( )=u+t v –u
( )t 0,1
[ ].
x 0
( )=uyx 1
( )=v ,luego u,v
[ ]= u+t v –u
( )/t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
x 0
( )= –2,–3
( )=u
t =1, x = 4,2
( )=v ,
u
v
u,v
[ ]= –2,–3
( )+t 6,5
( )/t 0,1
[ ]
{ }
. Por
lo tanto, el segmento de recta que une los puntos
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
y
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
está defi-
nido como, el siguiente subconjunto de 2
:
u,v 2
u v
u,v
x t
( )=u+t v –u
( )t 0,1
[ ].
x 0
( )=uyx 1
( )=v ,luego u,v
[ ]= u+t v –u
( )/t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
x 0
( )= –2,–3
( )=u
t =1, x = 4,2
( )=v ,
u
v
u,v
[ ]= –2,–3
( )+t 6,5
( )/t 0,1
[ ]
{ }
La ecuación vectorial de este segmento de recta está definido como
( ) ( ) [ ]
+
= ∈
x t t
t
–2,–3 ( )
6, 5 , 0,1
.
De manera general, sean u, v , 2
u v
con
u, v , 2
u v, la ecuación vectorial
del segmento de recta que une los puntos
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
,
0, i , j
( )
u,v 2
v 0
L= x t
( )=u+tv | t R
{ }
u
v
x
x t
( )=u+tv
t
está definida como
u,v 2
u v
u,v
x t
( )=u+t v –u
( ), t 0,1
[ ].
x 0
( )= uyx 1
( )=v , luego u,v
[ ]= u+t v –u
( )| t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t = –2,–3 +t 4,2 – –2,–3 = –2,–3 +t 6,5
. Nota que x 0
( )= u y x 1
( )=v, luego,
u,v 2
u v
u,v
x t
( )=u+t v –u
( ), t 0,1
[ ].
x 0
( )= uyx 1
( )=v , luego u,v
[ ]= u+t v –u
( )| t 0,1
[ ]
{ }.
u = –2,–3
( ),v = 4,2
( ),
x t
( )= –2,–3
( )+t 4,2
( )– –2,–3
( ) = –2,–3
( )+t 6,5
( )
Recuerda que…
Sean A, B dos puntos
distintos cualesquiera y
C
≅
2AB
≅
. Se dice que los tres
puntos A, B, C están alineados
o que son colineales.
u
j
u
j
+ t
y L
a x
0
u
v
v
v
y
x
W
x1
x0
L = u + W
[A, B]
(x, y)
b
y0
x0 a x
y
L
0
0
A
B
p Figura 4.4.
0
v
v
u
x
u
u
t
L
y
x x
y
j j
u
j
u
x(1)
L
x(–2)
–2 –1
–1
–2
0
j
+ t
y L
a x
0
u
v
v
v
y
x
W
x1
x0
L = u + W
[A, B]
(x, y)
b
y0
x0 a x
y
L
0
0
A
B 1 2 3 4 5
1
2
3
4
5
6
7
0
–1
–2
–3
A
B
x
y
[A, B]
p Figura 4.5.
t0 , t1
x0 = x t0
( )=u+tov ,x1= x t1
( )=u+t1v.
x0
x1
A,B
[ ]
AB
x0 , x1
[ ]
x0 = x t0
( )=u+tov ,x1= x t1
( )=u+t1v.
x0
x1
A,B
[ ]
AB
x0 , x1
[ ]
t0 , t1
x0 = x t0
( )=u+tov ,x1= x t1
( )=u+t1v.
x0
x1
A,B
[ ]
AB
x0 , x1
[ ]
x1
.
.
Recuerda que…
Para determinar la
ecuación vectorial de una recta,
es necesario conocer un punto
de la recta y un vector director
no nulo o dos puntos distintos
de la recta.
Dados el punto
u = –2,0
( ) y v = =
j 0,1
( ),
,
x = –2,0
( ) ( )
+t t
0,1
( )= –2,
t
( ) t
y el vector
u = –2,0
( ) y v = =
j 0,1
( ),
,
x = –2,0
( ) ( )
+t t
0,1
( )= –2,
t
( ) t
la ecuación vectorial de la recta
es
u = –2,0
( ) y v = =
j 0,1
( ),
,
x = –2,0
( ) ( )
+t t
0,1
( )= –2,
t
( ) t .
.
.
.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-68-320.jpg)
![180
DCCD: M.5.2.9. Escribir y reconocer la ecuación vectorial y paramétrica de una recta a partir de un punto de la recta y un vector dirección, o a partir
de dos puntos de la recta.
Ecuación paramétrica de la recta
Sean u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
con
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
≠ 0 y L el subconjunto de 2
definido así:
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
.
Como se ha dicho en las páginas precedentes, este conjunto L repre-
senta una recta que pasa por
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
y es paralela al vector
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +
(
x = x0 +ta,
y = y0 +tb,
t
. Una ecuación
vectorial de L está dada por:
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
De la definición del subconjunto L de 2
, se tiene la siguiente equiva-
lencia:
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
, tal que
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
Ponemos
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
con
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
≠ 0, es decir que al menos un
componente es no nulo. De la equivalencia precedente se sigue que
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
tal que
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv, t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
tal que
El par de ecuaciones
x = x0 +ta
,
,
y = y0 +tb se llama ecuaciones paramétricas
de la recta L, donde t R se conoce como parámetro de las ecua-
ciones que definen L.
Como dijimos, v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
esto es, al menos uno de los compo-
nentes es no nulo. Supongamos que a ≠ 0. De la ecuación
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –m
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
se obtiene
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
Reemplazando en la ecuación
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
y y
obtenemos el resultado siguiente:
.
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
La ecuación definida como:
(x, y) R2
tal que
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
.
se llama ecuación cartesiana de la recta L que pasa por
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 y
x,y
( ) 2
y es paralela a
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 y
x,y
( ) 2
y– y0 = m x– x0
( )
El número real
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
m=
b
a
.
se llama pendiente de la recta y se lo representa con
m =
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
b
. La ecuación cartesiana de la recta L se expresa como
(x, y) R2
tal que y – y0
= m(x – x0
),
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
m=
b
a
.
y– y0 = m x– x0
( ),
y = y0 –
bx0
a
+
b
a
x = y0 –mx0 +mx
y = a+mx
x ,
a= y0 –mx0 .
v.
a= 0,
v = a,b
( )
,
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
m=
b
a
.
y– y0 = m x– x0
( ),
y = y0 –
bx0
a
+
b
a
x = y0 –mx0 +mx
y = a+mx
x ,
a= y0 –mx0 .
v.
a= 0,
v = a,b
( )
que a su vez se escribe con
y = a + mx, x R, con a = y0
– mx0
.
En la Figura 4.6. se muestra la recta L que pasa por (x0
, y0
) y es paralela
al vector
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
m=
b
a
.
y– y0 = m x– x0
( ),
y = y0 –
bx0
a
+
b
a
x = y0 –mx0 +mx
y = a+mx
x ,
a= y0 –mx0 .
v.
a= 0,
v = a,b
( )
En el caso en que a = 0 , como
b
a
m=
b
a
.
x,y
( ) 2
y– y0 =
b
a
= x– x0
( )
u = x0 ,y0
( )
v = a,b
( ) 0,0
( ).
b
a
m=
b
a
.
, se tiene b ≠ 0.
En consecuencia, de las ecuaciones paramétricas de la recta L
se obtiene
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
y reemplazando en la ecuación
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x
(
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +m
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 y
se tiene la siguiente ecuación cartesiana de L:
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 , y .
x,y
( ) 2
0
v
v
u
x
u
u
t
L
y
x x
y
j j
u
j
u
x(1)
L
x(–2)
–2 –1
–1
–2
0
j
+ t
y L
a x
0
u
v
v
v
y
x
W
x1
x0
L = u + W
[A, B]
(x, y)
b
y0
x0 a x
y
L
0
0
A
B 1 2 3 4 5
1
2
3
4
5
6
7
0
–1
–2
–3
A
B
x
y
[A, B]
p Figura 4.6.
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
¿Cuál es la ecuación
general de la recta?
Saberes previos
Desequilibrio cognitivo
¿Por qué el estudio
de las ecuaciones cartesiana
y vectorial de la recta es
condición previa para el estudio
de derivadas?
Simbología matemática
El par de ecuaciones
u, v 2
v 0
L = x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
u, v 2
v 0
L= x t
( )=u+tv t
{ }
u
v
x t
( )=u+tv , t .
x = x,y
( ) L t
x =u+tv.
u = x0 ,y0
( ), v = a,b
( )
v 0,
x,y
( ) L t
x,y
( )= x0 + y0
( )+t a,b
( )= x0 +ta,y0 +tb
( )
x = x0 +ta,
y = y0 +tb,
t
se llaman ecuaciones paramé-
tricas de la recta L, donde la
variable t R se llama pará-
metro.
La ecuación definida como:
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
tal que
v = a,b
( ) 0,0
( ),
a 0.
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
x = x0 +ta= x0 ,
se llama ecuación cartesiana
de la recta L. También se expre-
sa como
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 y
x,y
( ) 2
y– y0 = m x– x0
( )
tal que
x = x0 +ta
t =
x– x0
a
.
y = y0 +tb,
y = y0 +
x x0
a
b y– y0 =
b
a
x– x0
( )
x,y
( ) 2
y– y0 =
a
b
x– x0
( ),
y– y0 =
bx0
a
+
b
a
x = y0 –mx0 +mx
x ,
y = a+mx
a= y0 –mx0 .
u = x0 ,y0
( )
v
a= 0,
v = a,b
( ) 0,0
( ).
b 0,
t =
y y0
b
.
.
x = x0 +ta= x0 ,
x = x0 +ta= x0 ,
x = x0 y
x,y
( ) 2
y– y0 = m x– x0
( )](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-69-320.jpg)


























![207
La pista de un aeropuerto tiene una lon-
gitud de 3 000 m. Para despegar, debe
alcanzar una velocidad de al menos 280
km/h en los primeros segundos.
La función de posición viene dada por
S (t) = 2t + 0,95t2
+ 0,11t3
, t ∈ [0, 60]
medida en metros.
7
Trabajen en sus cuadernos.
Diversidad funcional
en el aula
Es importante recordar que las personas que
tienen dificultad al expresarse oralmente no
deben ser interrumpidas. Tampoco necesitan
que alguien más termine sus oraciones.
Trabajo colaborativo
En una pista larga y recta, un automóvil
parte del reposo. Su velocidad, en m/s,
está dada por:
6
V t
( )=
1
2
t
t
2
,
33,6–0,2 ,
a) Analicen si en 30 segundos alcanza el avión
la velocidad mínima requerida.
b) Calculen la distancia recorrida en 30 segun-
dos.
c) Calculen la aceleración que alcanza el avión
en 30 segundos.
d) Encuentren qué distancia ha recorrido y
qué velocidad tiene el avión en 40 segun-
dos.
e) Investiguen a qué distancia del extremo del
aeropuerto se encuentra el avión al minuto
de haber iniciado el despegue.
a) Calculala velocidad y la aceleración en t = 5 s.
¿Existe aceleración al instante t = 10 s?
si t 8,
si t 8.
Supón que S(t) = 0,2 t2
, t 0 medida en
metros, t1
=10 s y t2
= 20 s. Indica cuáles
de las proposiciones siguientes son ciertas.
3
Los registros de un atleta lo conducen a
establecer la siguiente función de posición
medida en metros: S(t) = 3,9t; t ≥ 0.
Un automóvil parte del reposo y recorre
la distancia medida en metros
S(t) = 0,4t2
en los 10 primeros segundos.
Luego mantiene la velocidad constante
durante los 100 segundos siguientes.
4
5
a) Determina t, tal que S(t) = 20 000 m.
a) Calcula la velocidad y la aceleración a los
10 segundos.
b) Calcula la distancia total recorrida.
b) Calcula la velocidad media para los tiem-
pos t = 1 000 y t = 1 500.
a) S(t2
) es el doble de S(t1
). _________
b) S(t2
) es cuatro veces S(t1
). ________
c) V(t2
) es cuatro veces V(t1
).________
d) V(t1
) es la mitad de V(t2
). ________
e) a(t2
) es el doble de a(t1
). ________](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-96-320.jpg)
![208
Solución de problemas
cotidianos
Problema 1. Conexión con la física
1. La altura de un proyectil, t segun-
dos después de haber sido
lanzado verticalmente hacia
arriba a partir del suelo con
una velocidad inicial v0
me-
tros por segundo, está dada
por la función de posición:
f (t) = v0
t – 5t2
, t ≥ 0.
a) Prueba que la velocidad media del proyectil duran-
te el intervalo de tiempo t a t + h es v0
– 10t – 5h
metros por segundo, h ≠ 0.
b) Prueba que la velocidad instantánea del proyec-
til en el instante t es v0
– 10t metros por segundo.
Demostración
a) Sea: h ≠ 0. De la definición de f se tiene
f (t) = v0
t – 5t2
,
f (t + h) = v0
(t + h) – 5(t +h)2
.
La velocidad media Vh
se define como:
=
f t+h
( )– f t
, h ≠ 0.
, h ≠ 0,
, h ≠ 0.
( )
h
=
vo t+h
( )–5 t+h
( )
2
– vot–5t2
( )
h
=
vot+voth–5t2
–10th–5h2
–v0t+5t2
h
=
voh–10th–5h2
h
=vo –10t–5h
Vh
Vh
Vh
Vh
Vh
.
,
Entonces
=
f t+h
( )– f t
, h ≠ 0.
, h ≠ 0,
, h ≠ 0.
( )
h
=
vo t+h
( )–5 t+h
( )
2
– vot–5t2
( )
h
=
vot+voth–5t2
–10th–5h2
–v0t+5t2
h
=
voh–10th–5h2
h
=vo –10t–5h
Vh
Vh
Vh
Vh
Vh
.
,
Así
=
f t+h
( )– f t
, h ≠ 0.
, h ≠ 0,
, h ≠ 0.
( )
h
=
vo t+h
( )–5 t+h
( )
2
– vot–5t2
( )
h
=
vot+voth–5t2
–10th–5h2
–v0t+5t2
h
=
voh–10th–5h2
h
=vo –10t–5h
Vh
Vh
Vh
Vh
Vh
.
,
=
f t+h
( )– f t
, h ≠ 0.
, h ≠ 0,
, h ≠ 0.
( )
h
=
vo t+h
( )–5 t+h
( )
2
– vot–5t2
( )
h
=
vot+voth–5t2
–10th–5h2
–v0t+5t2
h
=
voh–10th–5h2
h
=vo –10t–5h
Vh
Vh
Vh
Vh
Vh
.
,
Se verifica la afirmación del literal a.
b) Tomamos valores de |h| cada vez más pequeños,
en la velocidad media:
=vo –10t
lím
lím
–5h,
= (vo–10t–5h).
=vo –10t.
216
km
h
Vh
0
h
Vh
V
Se obtiene
=vo –10t
lím
lím
–5h,
= (vo–10t–5h).
=vo –10t.
216
km
h
Vh
0
h
Vh
V
Se verifica el enunciado del literal b.
Nota que v =
df
dt
(t).
Tomado de:
http://www.konradlorenz.edu.co/images/stories/articulos/DESARRO-
LLO_DE_LA_DERIVADA_SIN_LA%20NOCION_DEL_LIMTE.pdf
Sigue estos pasos de experimentación, modela-
ción, interpretación y generalización para resolver los
siguientes problemas.
Problema 2. Conexión con economía
Encuentra cuánto costará producir 500 cajas de
banano en un mes, si la función de costo C (x) es igual
a C (x) = 3x + 0,004x2
+ c.
Problema 3. Conexión con transporte
La pista de un aeropuerto tiene una longitud de
3 000 m. Un avión de carga debe alcanzar una veloci-
dad mínima de
=vo –10t
lím
lím
–5h,
= (vo–10t–5h).
=vo –10t.
216
km
h
Vh
0
h
Vh
V
. La función de posición está
dada por:
S(t) = 0,05t + 0,2t2
+ 0,008t3
, t [0, 60] , medida en
metros.
a) Calcula el tiempo t en el que el avión alcanza la
velocidad de
=vo –10t
lím
lím
–5h,
= (vo–10t–5h).
=vo –10t.
216
km
h
Vh
0
h
Vh
V
.
b) Calcula la distancia recorrida en ese tiempo y su
aceleración.
c) Calcula la distancia recorrida, la velocidad y ace-
leración alcanzada al instante t = 60 s.
Problema 4. Conexión con física
Se lanza verticalmente hacia arriba una piedra, des-
pués de t segundos, su altura es h = 19,6t – 4,9t2
metros. Halla:
a) La velocidad inicial.
b) La velocidad después de 0,5; 1 y 2 segundos.
c) El tiempo de subida.
d) La altura máxima que alcanza la piedra.
e) La aceleración después de 1 segundo.
Grafica h en función del tiempo hasta el tiempo de
retorno.
Practica en tu cuaderno
Shutterstock,
(2020).
253434385
=
f t+h
( )– f t
, h ≠ 0.
, h ≠ 0,
, h ≠ 0.
( )
h
=
vo t+h
( )–5 t+h
( )
2
– vot–5t2
( )
h
=
vot+voth–5t2
–10th–5h2
–v0t+5t2
h
=
voh–10th–5h2
h
=vo –10t–5h
Vh
Vh
Vh
Vh
Vh
.
,
p Bala recubierta de cobre.
Shutterstock,
(2020).
77971306
p Pista de aeropuerto.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-97-320.jpg)



![212
Desafíos y proyectos matemáticos
Tema:Maximización
de costos y derivadas
Shutterstock,
(2020).
83105218
Objetivos
• Comprender los concep-
tos básicos del cálculo
diferencial.
• Iniciarse de manera natu-
ral en el manejo de deri-
vadas y darse cuenta de la
necesidad de usarlas para
encontrar la solución de
problemas reales.
• Valorar la utilidad de sus
conocimientos sobre de-
rivadas, y encontrar usos
adecuados en situaciones
de la vida real.
Justificación
La importancia del estudio de las derivadas radica en la posibilidad de
resolver situaciones en diversos ámbitos. Por ejemplo, en economía, en
temas como costos, consumo, demanda, utilidad, ahorro o maximiza-
ción de la producción.
Actividades
• Formarequiposdetrabajo,connomásdetresestudiantesporgrupo.
• Analizar el problema planteado como modelo, y proponer una
situación similar
Recursos
Modelo de problema resuelto
La gerente comercial de una empresa editorial estima que si el precio
de un libro es de $ 20, vende 10 000 ejemplares. Por cada dólar que se
incremente el precio, las ventas disminuyen en 400 ejemplares. ¿Qué
precio deberá fijar a cada libro, de manera que el ingreso para la em-
presa por la venta de estos libros sea el máximo? ¿Cuál es el valor de
dicho ingreso?
Solución: Los ingresos se calculan multiplicando el precio por el nú-
mero de ejemplares vendidos.
L = 20 × 10 000, donde L es el ingreso.
Si x representa el número de dólares que se incrementa el precio
de cada ejemplar, entonces 20 + x es el nuevo precio del libro y
10 000 – 4 000x es el nuevo número de ejemplares vendidos.
La función que representa el ingreso en términos del número de dó-
lares en que se aumenta el precio del libro es:
L (x) = (20 + x)(10 000 – 400x).
Esta función I(x), recibe el nombre de función objetivo porque es la
función que se requiere optimizar. La derivada de la función I(x) es:
L´(x) = (1)(10 000 – 400x) – 400(20 + x),
L´(x) = 10 000 – 400x – 8 000 – 400 x,
L´(x) = –8 00x + 2 000,
L´(x) = 0 ⇒ 800 x = 2 000,
x =
2000
800
;x =2,5 .
Recordemos que x representa el número de dólares en que se debe
incrementar el precio del libro para obtener el ingreso máximo.
De esta manera, al incrementar el precio de venta del libro en $ 2,5, se
obtiene el ingreso máximo. Para calcular el ingreso máximo se susti-
tuye x en la función L(x).
L (2,5) = (20 + 2,5) [10 000 – 400(2,5)]
L (2,5) = (22,5) [10 000 – (1 000)
L (2,5) = 202 500,00
Este valor representa el máximo ingreso.
Adaptado de http://www.mat.uson.mx/~jldiaz/contenido_Derivadas.html
Conclusiones
Es importante recuperar la importancia de realizar cálculos reales
cuando se trata de emprender una empresa.
p Textos de investigación.
Glosario
optimizar. Buscar la
mejor manera de realizar una
actividad.
a
cb](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-101-320.jpg)







![220
Designamos con 0, al ángulo que forman estos dos vec-
tores. Sea P = (x, y) R2
un punto cualquiera de la bisectriz R. En la
Figura 5.5. se muestran las dos rectas R A C C tA t
t
P t
R B D D tB t
( , )= | ,
( )
( , )= ,| ,
1
2
{ }
{ }
+ ∈
∈
∈
+ ∈
y
R A C C tA t
t
P t
R B D D tB t
( , )= | ,
( )
( , )= ,| ,
1
2
{ }
{ }
+ ∈
∈
∈
+ ∈
y los puntos
seleccionados M y N , así como el punto P en la bisectriz R.
Los ángulos 1
y 2
formados por los vectores QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
, así como
por
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
, son congruentes. Esto es,
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
, con lo que
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
entonces,
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
. En la Figura
5.6. se exhiben los ángulos congruentes que forman los tres vectores
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
,
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
, y su medida común
QP y QM
QP y QN
MQP PQN
m MQP m PQN
α α
α α
α
( ) ( )
≅
= , = ,
= =
2
.
1 2
1 2
.
De la definición del ángulo que forman dos vectores, se sigue
QP QM
QP QM
QP QN
QP QN
cos = , cos =
1 2
.
α α
( ) ( )
⋅ ⋅
Luego,
QP QM
QP QM
QP QN
QP QN
α α
( ) ( ) ⋅ ⋅
cos = cos = .
1 2
De esta última igualdad, se simplifica QP
≠ 0, con lo que se obtiene
= , = 0.
⋅ ⋅
⋅ −
QP QM
QM
QP QN
QN
QP
QM
QM
QN
QN
y de esta se deduce la siguiente ecuación:
= , = 0.
⋅ ⋅
⋅ −
QP QM
QM
QP QN
QN
QP
QM
QM
QN
QN
Puesto que QP P Q
−
= ,
resulta
Q
0 M
R1
R2
N
P
R
y
x
p Figura 5.5.
a
2
a
2
0
Q
QM
QP
QN
N
y
x
p Figura 5.6.
= 0 =
, = , .
γ β
( )
( ) ( )
− ⋅ − ⋅ − ⋅ −
⋅ − ⋅ −
P Q
QM
QM
QN
QN
P
QM
QM
QN
QN
Q
QM
QM
QN
QN
x y
QM
QM
QN
QN
QM
QM
QN
QN
⇔
⇔
Esta última igualdad define la ecuación cartesiana de la bisectriz R del
ángulo [0, π], formado por las rectas R A C C tA t
t
P t
( , )= | ,
( )
1
{ }
+ ∈
∈
∈
y
R A C C tA t
t
P t
R B D D tB t
( , )= | ,
( )
( , )= ,| ,
1
2
{ }
{ }
+ ∈
∈
∈
+ ∈
.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-109-320.jpg)

![222
La ecuación cartesiana de la bisectriz está definida como sigue:
x y x y
QM
QM
QN
QN
QM
QM
QN
QN
( , ) tal que ( , ) =( , ) .
2
∈ ⋅ −
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟ γ β ⋅ −
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
R
Tenemos los siguientes resultados:
= =(0, 1)
18
7
,
16
7
=
18
7
,
9
7
,
=
18
7
9
7
=
9 5
7
,
= =(0,2)
18
7
,
16
7
=
18
7
,
30
7
,
=
18
7
30
7
=
6 34
7
,
2 2
2 2
QM M Q
QM
QN N Q
QN
− − − − −
− +
− − − −
+
QM
QM
QN
QN
x y
x y
=
7
9 5
18
7
,
9
7
7
6 34
18
7
,
30
7
=
2 5
5
3 34
34
,
5
5
5 34
34
.
( , )
2 5
5
3 34
34
,
5
5
5 34
34
=
18
7
,
16
7
2 5
5
3 34
34
,
5
5
5 34
34
,
2 5
5
3 34
34
5
5
5 34
34
=
52
35
5
67
119
34.
− − − − − + −
⋅ − + − − ⋅ − + −
− + + − − +
QM
QM
QN
QN
x y
x y
=
7
9 5
18
7
,
9
7
7
6 34
18
7
,
30
7
=
2 5
5
3 34
34
,
5
5
5 34
34
.
( , )
2 5
5
3 34
34
,
5
5
5 34
34
=
18
7
,
16
7
2 5
5
3 34
34
,
5
5
5 34
34
,
2 5
5
3 34
34
5
5
5 34
34
=
52
35
5
67
119
34.
− − − − − + −
⋅ − + − − ⋅ − + −
− + + − − +
Reemplazando en la ecuación cartesiana de la bisectriz, se obtiene
QM
QM
QN
QN
x y
x y
=
7
9 5
18
7
,
9
7
7
6 34
18
7
,
30
7
=
2 5
5
3 34
34
,
5
5
5 34
34
( , )
2 5
5
3 34
34
,
5
5
5 34
34
=
18
7
,
16
7
2 5
5
3 34
34
,
5
5
5 34
34
2 5
5
3 34
34
5
5
5 34
34
=
52
35
5
67
119
34.
− − − − − + −
⋅ − + − − ⋅ − + −
− + + − − +
en donde
Archivo
editorial,
(2020).
Geogebra
Conexiones con las TIC
Existen softwares libres,
como, por ejemplo, GeoGebra,
que permiten el cálculo de las
bisectrices de un ángulo.
Ejercicio resuelto 3
Sean R1
, R2
dos rectas definidas como
= ( , ) | 2 2 = 0 , = ( , ) |5 3 6 = 0 .
1
2
2
2
R x y x y R x y x y
{ } { }
∈ + + ∈ + −
= ( , ) | 2 2 = 0 , = ( , ) |5 3 6 = 0 .
1
2
2
2
R x y x y R x y x y
{ } { }
∈ + + ∈ + −
Estas dos rectas se cortan en el punto, que es solución del sistema de
ecuaciones
2 2 = 0,
5 3 6 = 0.
x y
x y
+ +
+ −
Así, obtenemos =(
18
7
,
16
7
) =( , )
Q
− γ β
=(
18
7
,
16
7
) =( , )
Q
− γ β
=(
18
7
,
16
7
) =( , )
Q
− γ β .
Para x = 0, reemplazando en la ecuación de la recta R1
, obtenemos
y = –1 y, reemplazando en la ecuación de la recta R2
, resulta y = 2. Así,
M R N R
[ ]
− ∈ ∈
α ∈ π
=(0, 1) , =(0,2) .
0,
1 2
Consideramos el ángulo
M R N R
[ ]
− ∈ ∈
α ∈ π
=(0, 1) , =(0,2) .
0,
1 2
que forman estas dos rectas. En
la Figura 5.8. se muestran las rectas R1
, R2
, la bisectriz y los vectores
y .
QM QN
1 2
3
2
1
0
–1
–2 Q
N
QN
QM
M
18
7
16
7
–
R
R1
R2
y
x
p Figura 5.8.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-111-320.jpg)



![226
A + B
A – B
A – B
A
B
–B
–B
B
A
0 x
y
p Figura 5.12.
Sean A B
A B A B A B
A B A B A B
A A A B B B
A A B B
A B A B A B
A A B B
A B A B A B
,
=2 .
=( ) ( )
= 2( )
= 2( ) ,
=( ) ( )
= 2( ) ,
=2 .
2
2 2
2 2 2 2
2
2 2
2
2 2
2 2
R
∈
+ + − +
+ + ⋅ +
⋅ + ⋅ + ⋅
+ ⋅ +
− − ⋅ −
− ⋅ +
+ + − +
. En la Figura 5.12. se muestran los vectores
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
,
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
y los
vectores A B
A B
+
−
y
A B
A B
+
− que forman las diagonales del paralelogramo.
También se muestran los vectores
A B
A B
+
− y
A B
A B
+
− .
Un resultado muy conocido de la geometría plana es el famoso teorema
de Pitágoras que se enuncia como sigue: en todo triángulo rectángulo,
la hipotenusa al cuadrado es igual a la suma de los cuadrados de los
catetos. Este resultado es extendido al espacio euclídeo R2
.
Teorema de Pitágoras
Sean A B
A B A B A B
A B A B A B
A A A B B B
A A B B
A B A B A B
A A B B
A B A B A B
,
=2 .
=( ) ( )
= 2( )
= 2( ) ,
=( ) ( )
= 2( ) ,
=2 .
2
2 2
2 2 2 2
2
2 2
2
2 2
2 2
R
∈
+ + − +
+ + ⋅ +
⋅ + ⋅ + ⋅
+ ⋅ +
− − ⋅ −
− ⋅ +
+ + − +
. Entonces,
= .
2 2 2
A B
A B A B
⊥
+ +
si y solo si
= .
2 2 2
A B
A B A B
⊥
+ +
Demostración. Debemos probar una equivalencia.
) Supongamos que
= .
2 2 2
A B
A B A B
⊥
+ +
. Por la definición de vectores perpen-
diculares, se tiene
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
. Luego, de la definición de norma y de las
propiedades del producto escalar, se deduce
=( ) ( )
= 2 = .
2
2 2
A B A B A B
A A A B B B A B
+ + ⋅ +
⋅ + ⋅ + ⋅ +
) Recíprocamente, sean A B
A B A B A B
A B A B A B
A A A B B B
A A B B
A B A B A B
A A B B
A B A B A B
,
=2 .
=( ) ( )
= 2( )
= 2( ) ,
=( ) ( )
= 2( ) ,
=2 .
2
2 2
2 2 2 2
2
2 2
2
2 2
2 2
R
∈
+ + − +
+ + ⋅ +
⋅ + ⋅ + ⋅
+ ⋅ +
− − ⋅ −
− ⋅ +
+ + − +
, tal que =( ) ( )
= 2 = .
2
2 2
A B A B A B
A A A B B B A B
+ + ⋅ +
⋅ + ⋅ + ⋅ +
=( ) ( )
= 2 = .
2
2 2
A B A B A B
A A A B B B A B
+ + ⋅ +
⋅ + ⋅ + ⋅ + .
Nuevamente, de la definición de norma y de las propiedades del pro-
ducto escalar, se obtiene
= 2 .
= 2 = .
2 2 2
2 2 2 2 2
+ + ⋅ +
+ + ⋅ + +
A B A A B B
A B A A B B A B
De esta igualdad y por la hipótesis, resulta que
= 2 .
= 2 = .
2 2 2
2 2 2 2 2
+ + ⋅ +
+ + ⋅ + +
A B A A B B
A B A A B B A B
Por la ley cancelativa de la adición (cancelando
=( ) ( )
= 2 = .
2
2 2
A B A B A B
A A A B B B A B
+ + ⋅ +
⋅ + ⋅ + ⋅ + ), se sigue
que
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
con lo cual
= .
2 2 2
A B
A B A B
⊥
+ +
.
Ley de los cosenos
Teorema
Sean A B
A B A B A B
A B A B A B
A A A B B B
A A B B
A B A B A B
A A B B
A B A B A B
,
=2 .
=( ) ( )
= 2( )
= 2( ) ,
=( ) ( )
= 2( ) ,
=2 .
2
2 2
2 2 2 2
2
2 2
2
2 2
2 2
R
∈
+ + − +
+ + ⋅ +
⋅ + ⋅ + ⋅
+ ⋅ +
− − ⋅ −
− ⋅ +
+ + − +
no nulos y 0,
[ ]
θ ∈ π el ángulo que forman los vec-
tores
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
y
B
A B
A
B
A
A B
A B
B B
B
.
. =0
,
=0.
. =0,
=
=0
=0
2
2
2
∈
∈
∈
⋅
. Entonces,
= 2 cos( ).
=( ) ( )
= 2( )
= 2( ) .
2 2 2
2
2 2
− + − θ
− − ⋅ −
⋅ − ⋅ + ⋅
− ⋅ +
B A B A A B
B A B A B A
B B A B A A
B A B A
Demostración. De la definición del producto escalar, se tiene
= 2 cos( ).
=( ) ( )
= 2( )
= 2( ) .
2 2 2
2
2 2
− + − θ
− − ⋅ −
⋅ − ⋅ + ⋅
− ⋅ +
B A B A A B
B A B A B A
B B A B A A
B A B A
p Sismo provincia de Manabí 2016.
Sismo
Manabí,
(2020).
www.flirckagenciaandes_ec
Interdisciplinariedad
Los geólogos usan el
teorema de Pitágoras cuando
se rastrea la actividad de un
terremoto. Los terremotos
tienen dos tipos de ondas: una
que es más lenta que la otra.
Al triangular la distancia recorri-
da por la onda más rápida con
la correspondiente a la onda
más lenta, los geólogos pueden
determinar el centro o la fuente
del terremoto.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-115-320.jpg)




![231
Ejercicios resueltos
1. Consideremos el polinomio P definido como P(t) = 50, tR.
Se tiene que P es un polinomio de grado 0.
El único coeficiente no nulo de P(t) es a0
= 50.
Calculemos algunos valores de P(t) para tR. Así,
P(0) = 50,
P(10) = 50,
P(1 000) = 50.
2. Sea Q el polinomio definido como Q(t) = 3 + 8t, tR. Resulta
que Q es un polinomio de grado 1.
Los coeficientes de Q(t) son a0
= 3, a1
= 8.
Calculemos algunos valores Q(t) para tR.
Q(0) = 3 + 8 × 0 = 3,
Q(8) = 3 + 8 × 8 = 67,
Q(50) = 3 + 8 × 50 = 403.
3. El polinomio R(t) =15t + 208t2
, tR es un polinomio de grado 2.
Sus coeficientes son a0
= 0, a1
=15, a2
= 208.
Utilicemos el esquema de Hörner para calcular algunos va-
lores de R(t) con t R. Tenemos R(t) = t(15 + 208t). Luego,
R(1) = 1 × (15 + 208 × 1) = 223,
R(20) = 20 × (15 + 208 × 20) = 20 × (15 + 4 160) = 20 × 4 175 = 83 500.
4. Dado P(t) = 3 + 2t – 8t2
– 7t3
, tR, observamos que este es un
polinomio de grado 3, ordenado de forma creciente con respecto
de las potencias de t.
Mediante el esquema de Hörner, la escritura de P(t) es
P(t) = 3 + t(2 + t(–8 – 7t)). Calculemos algunos valores de P(t):
P(0) = 3 + 0(2 + 0(–8 – 7 × 0)) = 3,
P(–2) = 3 + (–2)(2 + (–2)(–8 – 7(–2))) =23,
P(–10) = 3 + (–10)(2 + (–10)(–8 –7(–10))) = 6 183,
P(5) = 3 + 5(2 + 5(–8 – 7 × 5)) = – 1 062.
5. Consideremos el polinomio P(t) siguiente: P(t) = 1 + 2t + 5t2
+ 4t3
+
7t4
, tR. Escribamos P(t) en la forma del esquema de Hörner:
P(t) =1 + t(2 + t(5 + t(4 + 7t))), tR.
Por ejemplo, para t =10 , tenemos
P(10)=1+10(2+10(5+10(4+7×10)))=1+10(2+10(5+10×74))
=1 + 10(2 + 10 × 745) =1 + 10 × 745 274 521 = 74 521.
Obsérvese que el cálculo de P(10) se inicia desde el paréntesis más
interno hacia los más externos.
6. Sea P el polinomio definido como P(x) = x2
+ x4
+ x5
+ x6
, xR.
Apliquemos el esquema de Hörner. Entonces tenemos
P(x)=x2
+x4
+x5
+x6
=x2
+x4
(1+x(1+x))=x2
(1+x2
(1+x(1+x))), xR.
Calculemos P(2) y P(5) usando este esquema. De esta manera,
tenemos
P(2) = 22
(1 + 22
(1 + 2(1 + 2))) = 22
(1 + 22
(1 + 2 × 3)) =
22
(1 + 4 × 7) = 4 × 29 = 116,
P(5) = 52
(1 + 52
(1 + 5(1 + 5))) = 52
(1 + 52
(1 + 30)) = 52
(1 + 25 × 31)
= 25 × 776 = 19 400.
Recuerda que…
Al conjunto constituido
por todos los polinomios en
con coeficientes en lo deno-
tamos con [ ]
k R .
Asumiremos que cada elemen-
to está ordenado de forma
creciente o decreciente con
respecto de las potencias de t
de la variable, en nuestro caso t.
El polinomio P se dice de grado
1 si grad(P) = 1, de grado 2 si
grad (P) = 2, de tercer grado si n
= 3, y así sucesivamente.
Conexiones con las TIC
Para efectuar cálculo
de operaciones combinadas
donde existen varios signos de
agrupación, puedes emplear
una calculadora científica.
Shutterstock,
(2020).
73329937
p Calculadora científica.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-120-320.jpg)
![232
Igualdad de polinomios
Definición
Sean P, Q [ ]
k R ] con
P t a a t a t
Q t b b t b t
t
n
n
m
m
,
,
.
0 1
0 1
( )
( )
= + +⋅⋅⋅+
= + +⋅⋅⋅+
∀ ∈
P t a a t a t
Q t b b t b t
t
n
n
m
m
,
,
.
0 1
0 1
( )
( )
= + +⋅⋅⋅+
= + +⋅⋅⋅+
∀ ∈
Diremos que P = Q si y solo si grad(P) = grad(Q) = m = n; y, ai
= bi
,
i = 0,1, ..., n.
Un polinomio queda perfectamente bien definido si se conocen sus
coeficientes a0
, a1
, ..., an
R.
Operaciones con polinomios
En el conjunto [ ]
k R definiremos dos operaciones internas: adición
y producto.
Adición
Sean a, b, k, tR. Los monomios atk
y btk
son semejantes. Su suma es
atk
+ btk
= (a + b)tk
.
Consideremos los polinomios en R con coeficientes en R siguientes,
escritos en forma creciente con relación a las potencias de t:
P t a a t a t t
Q t b b t b t t
m
m
n
n
, ,
, .
0 1
0 1
( )
( )
= + +⋅⋅⋅+ ∀ ∈
= + +⋅⋅⋅+ ∀ ∈
Definiremos la suma de los polinomios P(t) y Q(t). Para el efecto, con-
sideramos dos casos.
Caso I. Si m = n. La suma de P(t) con Q(t) se define en la forma habi-
tual de funciones reales como:
(P + Q)(t) = P(t) + Q(t),
P t a a t a t t
Q t b b t b t t
m
m
n
n
, ,
, .
0 1
0 1
( )
( )
= + +⋅⋅⋅+ ∀ ∈
= + +⋅⋅⋅+ ∀ ∈
donde
(P + Q)(t) = P(t) + Q(t) = a0
+ b0
+ (a1
+ b1
)t + ... +(an
+ bn
)tn
,
P t a a t a t t
Q t b b t b t t
m
m
n
n
, ,
, .
0 1
0 1
( )
( )
= + +⋅⋅⋅+ ∀ ∈
= + +⋅⋅⋅+ ∀ ∈
Nótese que la suma de polinomios se la hace para cada punto tR.
Caso II. Si m n. Podemos asumir que los coeficientes del polinomio
Q(t) de los términos de mayor grado que n hasta m inclusive son
nulos, es decir que bn+1
= 0, bn+2
= 0, ..., bm
= 0. Entonces,
Q(t) = b0
+ b1
t + ... + bn
tn
+ 0tn+1
+ ... + 0tn
,
P t a a t a t t
Q t b b t b t t
m
m
n
n
, ,
, .
0 1
0 1
( )
( )
= + +⋅⋅⋅+ ∀ ∈
= + +⋅⋅⋅+ ∀ ∈
La suma de los polinomios P(t) y Q(t) se realiza del mismo modo que
en el caso I.
Ejercicios resueltos
1. Sean P, Q los polinomios siguientes:
P t t t t
Q t t t t
P t t t t t
Q t t t t t
2–5 8 , ,
–5 7 , .
2–5 8 0 0
–5 0 7 0 .
2
2 4
2 3 4
2 3 4
( )
( )
( )
( )
= + ∀ ∈
= + + ∀ ∈
= + + +
= + + + +
Entonces,
(P + Q)(t) = P(t) + Q(t) = –3 – 5t + 15t2
+ t4
,
P t a a t a t t
Q t b b t b t t
m
m
n
n
, ,
, .
0 1
0 1
( )
( )
= + +⋅⋅⋅+ ∀ ∈
= + +⋅⋅⋅+ ∀ ∈
Recuerda la definición
Teorema
Hay que tener presente que si
P es un polinomio de grado
≤ n, para cada tR, P(t)R,
las operaciones de adición,
producto y producto por esca-
lares de polinomios heredan las
propiedades de la adición y del
producto en R.
El conjunto de polinomios con
coeficiente real y con la opera-
ción adición es un grupo abelia-
no, es decir que se verifican las
propiedades siguientes:
1. Conmutativa: para todo
P, Q polinomios con coefi-
ciente real,
P + Q = Q + P.
2. Asociativa: para todo
P, Q, R polinomios con coe-
ficiente real,
P + (Q + R) = (P + Q) + R.
3. Existencia de un elemento
neutro (polinomio nulo):
existe 0 elemento de los
polinomios con coeficiente
real, tal que para todo P
P + 0 = 0 + P = P.
4. Existencia de opuestos
aditivos: para todo
P elemento de los polino-
mios con coeficiente real,
existe Q elemento de los
polinomios con coeficiente
real, tal que P + Q = 0.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-121-320.jpg)



![236
Multiplicación de polinomios
DCCD: M.5.1.39. Realizar operaciones de multiplicación, entre funciones polinomiales, y multiplicación de números reales por polinomios, en ejercicios
algebraicos de simplificación.
Producto
Sean a, b, n, m, tR. Utilizando las propiedades del producto de nú-
meros reales, así como la potenciación de números reales con expo-
nentes naturales, el producto de los monomios atn
y btm
nos da el
resultado siguiente:
at bt abt t abt
n m n m n m
( )( ) = = .
+
Sean P, Q [ ]
k R . Pongamos
= , ,
= , .
0 1
0 1
( )
( )
+ + + ∈
+ + + ∈
P t a a t a t t
Q t b b t b t t
n
n
m
m
Sean j, k N y t R. Entonces, tj
tk
= tj+k
. La multiplicación de P con
Q se denota con PQ y se define como sigue:
PQ t P t Q t a a t a t b b t b t
a b a b a b t a b a b t a b t
n
n
m
m
n m n m
m n
n m
m n
( )( ) = ( ) ( ) =
= .
0 1 0 1
0 0 1 0 0 1 1 1
1
( )( )
( ) ( ) ( )
× + + + + + +
+ + + + + +
− −
+ − +
Nótese que el producto de dos polinomios es otro polinomio, es de-
cir que si P, Q [ ]
k R , entonces, P, Q [ ]
k R . Además, si grad (P) = m
y grad (Q) = n, entonces, grad (PQ) = m + n.
Se define la operación producto “.” en [ ]
k R como la función a cada
par de polinomios P, Q de [ ]
k R le asigna un único polinomio P . Q
antes definido:
Potencia de polinomios
Sea P [ ]
k R . Las potencias P0
, P1
, P2
, ... se definen a continuación.
Para todo t R,
(P0
)(t) = 1 si P(t) ≠ 0,
(P1
)(t) = P(t),
(P2
)(t) = P(t) × P(t),
(P3
)(t) = P(t)2 × P(t).
En general, si k N, para todo t R, (Pk+1
)(t) = (Pk
)(t)P(t).
Ejemplos
1. Sea P el polinomio definido por P(t) = 8t6
– 7t4
, t R. Entonces,
P1
(t) = P(t) = t4
(8t2
– 7),
P2
(t) = P(t) P(t) = [t4
(8t2
– 7)]2
= t8
(8t2
– 7)2
= 64t12
– 112t10
+ 49t8
,
P3
(t) = (P2
)(t)P(t) = t8
(8t2
– 7)2
[t4
(8t2
– 7)] = t12
(8t2
– 7)3
= 512t18
+ 1 344t16
+ 1 176t14
+ 343t12
.
Saberes previos
¿Qué es un polinomio de
grado menor o igual que n?
Desequilibrio cognitivo
¿Cuál es la relación entre
la multiplicación y la potencia-
ción?
Recuerda que…
El producto de polino-
mios satisface las propieda-
des siguientes:
i. Conmutativa: para todo
P, Q k R], PQ = QP.
ii. Asociativa: para todo
P, Q , R k R], P(QR) = (PQ)R.
iii. Existencia del elemento
unidad: existe 1 [ ]
k R ,
tal que para todo P [ ]
k R ,
1P = P.
iv. Distributiva: para todo
P, Q [ ]
k R ,
P(Q + R) = PQ + PR.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-125-320.jpg)
![237
Recuerda que…
Teorema
Sean P, Q k[R] y a, b R.
Se verifican las propiedades
siguientes:
i. (ab)P = a(bP) =
= b(aP) = abP.
ii. a(P + Q) = aP + aQ.
iii. (a + b)P = aP + bP.
iv. 1.P = P (1R).
v. (–1)P = – P.
Las operaciones de adición
y producto en R están relacio-
nadas mediante la propiedad
distributiva.
El conjunto [ ]
k R en el que
se ha definido la operación de
adición con la que
( [ ]
k R , +) es grupo conmuta-
tivo (página 232) y el producto
de números reales por polino-
mios de [ ]
k R que verifica las
propiedades indicadas arriba,
en el teorema, tiene estruc-
tura de espacio vectorial real,
llamadas espacio vectorial real
de polinomios.
Producto de números reales por polinomios
Sean a R, P [ ]
k R , el polinomio
P(t) = a0
+ a1
t + ... + an
tn
, tR.
El producto de a por P se nota aP y se define del modo siguiente:
para todo t R,
(aP)(t) = aP(t) = aa0
+ aa1
t + ... + aan
tn
.
Nótese que si a R y P [ ]
k R , aP [ ]
k R .
Ejercicios resueltos
1. Si a = –8 y P = 2 – 3t + 8t2
, tR, el polinomio aP está definido
por: (–8P)(t) = –8(2–3t + 8t2
) = – 16 + 24t – 64t2
.
2. Sean P, Q los polinomios siguientes:
P(t) = 2–4t + 8t2
, Q(t) = –9 + 4t – 2t3
.
Calcula (5P – 3Q)(1).
Solución
Determinemos los polinomios 5P, –3Q y 5P – 3Q. A este último lo
escribimos usando el esquema de Hörner. Así, tenemos
( )( ) ( ) ( ) ,
40
20
10
=
8
4
2
5
=
5
=
5 2
2
t
t
t
t
t
P
t
P +
+
( )( ) ( ) ( ) .
6
12
27
=
2
4
9
3
=
3
=
3 3
3
t
t
t
t
t
Q
t
Q +
+
( )( ) ( )
( ).
6
40
32
37
=
6
40
32
37
=
6
12
27
40
20
10
=
3
5
3
2
3
2
t
t
t
t
t
t
t
t
t
t
t
Q
P +
+
+
+
+
+
+
+
– –
– – –
–
–
– – – – –
–
Luego,
,
40 2
t
+
.
6
12 3
t
t +
( )
( ).
6
40
32
37
=
6
40
32
3
2
t
t
t
t
t
t +
+
+
+
+
–
–
( )( ) ( ) ( ) ,
40
20
10
=
8
4
2
5
=
5
=
5 2
2
t
t
t
t
t
P
t
P +
+
( )( ) ( ) ( ) .
6
12
27
=
2
4
9
3
=
3
=
3 3
3
t
t
t
t
t
Q
t
Q +
+
( )( ) ( )
( ).
6
40
32
37
=
6
40
32
37
=
6
12
27
40
20
10
=
3
5
3
2
3
2
t
t
t
t
t
t
t
t
t
t
t
Q
P +
+
+
+
+
+
+
+
– –
– – –
–
–
– – – – –
–
Para t = 1, se tiene
( )( ) ( )
( ) 51.
=
6
40
1
32
1
37
=
1
3
5 +
+
+
Q
P
( ) 6,
=
1
P ( ) ( )( ) ( ) ( )( ) ( ) 21,
=
1
3
=
1
3
30,
=
1
5
=
1
5
7,
=
1 Q
Q
P
P
Q
( ) ( ) ( )( ).
1
3
5
=
51
=
21
30
=
1
3
1
5 Q
P
Q
P +
–
–
–
– –
–
–
Nótese que
( )( ) ( )
( ) 51.
=
6
40
1
32
1
37
=
1
3
5 +
+
+
Q
P
( ) 6,
=
1
P ( ) ( )( ) ( ) ( )( ) ( ) 21,
=
1
3
=
1
3
30,
=
1
5
=
1
5
7,
=
1 Q
Q
P
P
Q
( ) ( ) ( )( ).
1
3
5
=
51
=
21
30
=
1
3
1
5 Q
P
Q
P +
–
–
–
– –
–
–
3. Sean P, Q los polinomios ( ) ( ) .
2
3
2
=
,
3
2
=
2
t
t
t
Q
t
t
P +
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
–
–
Verificar que
( ) ( ) .
2
3
2
=
,
3
2
=
2
t
t
t
Q
t
t
P +
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
–
–
Solución
Calculemos (P + Q)2
con tR. Tenemos
( ) ( ) ( )( ) ( )( ) ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
[ ]2
2
=
=
= t
Q
t
P
t
Q
t
P
t
Q
t
P
t
Q
P
t
Q
P
t
Q
P +
+
+
+
+
+
( ) ( ) .
.
4
=
2
=
2
3
2
3
2
= 4
2
2
2
2
t
t
t
t
t +
+
+
( ) ( ) .
4
=
4
2
t
t
Q
P +
( )( ) ( ) ( ) ( ) ( )
t
Q
t
Q
t
P
t
P
t
Q
PQ
P
2
2
2
2
2
=
2 +
+
+
+
( ) ( )( ) ( )2
2
2
2
2
3
2
2
3
2
3
2
2
3
2
= t
t
t
t
t
t +
+
+
+
+
+
( )
3
2
2
2
3
2
4
2
6
9
6
4
6
4
2
12
9
4
12
8
12
4
9
4
= t
t
t
t
t
t
t
t
t
t
t
t +
+
+
+
+
+
+
+
+
( ) ( ) ( )( ),
2
=
4
=
2
2
4
2
t
Q
PQ
P
t
4
=
4
t
t
Q
P +
+
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
Así,
( ) ( ) ( )( ) ( )( ) ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
[ ]2
2
=
=
= t
Q
t
P
t
Q
t
P
t
Q
t
P
t
Q
P
t
Q
P
t
Q
P +
+
+
+
+
+
( ) ( ) .
.
4
=
2
=
2
3
2
3
2
= 4
2
2
2
2
t
t
t
t
t +
+
+
( ) ( ) .
4
=
4
2
t
t
Q
P +
( )( ) ( ) ( ) ( ) ( )
t
Q
t
Q
t
P
t
P
t
Q
PQ
P
2
2
2
2
2
=
2 +
+
+
+
( ) ( )( ) ( )2
2
2
2
2
3
2
2
3
2
3
2
2
3
2
= t
t
t
t
t
t +
+
+
+
+
+
( )
3
2
2
2
3
2
4
2
6
9
6
4
6
4
2
12
9
4
12
8
12
4
9
4
= t
t
t
t
t
t
t
t
t
t
t
t +
+
+
+
+
+
+
+
+
( ) ( ) ( )( ),
2
=
4
=
2
2
4
2
t
Q
PQ
P
t
4
=
4
t
t
Q
P +
+
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
Por otro lado,
( ) ( ) ( )( ) ( )( ) ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
[ ]2
2
=
=
= t
Q
t
P
t
Q
t
P
t
Q
t
P
t
Q
P
t
Q
P
t
Q
P +
+
+
+
+
+
( ) ( ) .
.
4
=
2
=
2
3
2
3
2
= 4
2
2
2
2
t
t
t
t
t +
+
+
( ) ( ) .
4
=
4
2
t
t
Q
P +
( )( ) ( ) ( ) ( ) ( )
t
Q
t
Q
t
P
t
P
t
Q
PQ
P
2
2
2
2
2
=
2 +
+
+
+
( ) ( )( ) ( )2
2
2
2
2
3
2
2
3
2
3
2
2
3
2
= t
t
t
t
t
t +
+
+
+
+
+
( )
3
2
2
2
3
2
4
2
6
9
6
4
6
4
2
12
9
4
12
8
12
4
9
4
= t
t
t
t
t
t
t
t
t
t
t
t +
+
+
+
+
+
+
+
+
( ) ( ) ( )( ),
2
=
4
=
2
2
4
2
t
Q
PQ
P
t
4
=
4
t
t
Q
P +
+
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
En consecuencia, para todo t R,
( ) ( ) ( )( ) ( )( ) ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
[ ]2
2
=
=
= t
Q
t
P
t
Q
t
P
t
Q
t
P
t
Q
P
t
Q
P
t
Q
P +
+
+
+
+
+
( ) ( ) .
.
4
=
2
=
2
3
2
3
2
= 4
2
2
2
2
t
t
t
t
t +
+
+
( ) ( ) .
4
=
4
2
t
t
Q
P +
( )( ) ( ) ( ) ( ) ( )
t
Q
t
Q
t
P
t
P
t
Q
PQ
P
2
2
2
2
2
=
2 +
+
+
+
( ) ( )( ) ( )2
2
2
2
2
3
2
2
3
2
3
2
2
3
2
= t
t
t
t
t
t +
+
+
+
+
+
( )
3
2
2
2
3
2
4
2
6
9
6
4
6
4
2
12
9
4
12
8
12
4
9
4
= t
t
t
t
t
t
t
t
t
t
t
t +
+
+
+
+
+
+
+
+
( ) ( ) ( )( ),
2
=
4
=
2
2
4
2
t
Q
PQ
P
t
4
=
4
t
t
Q
P +
+
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+
que muestra que
( ) ( ) ( )( ) ( )( ) ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
[ ]2
2
=
=
= t
Q
t
P
t
Q
t
P
t
Q
t
P
t
Q
P
t
Q
P
t
Q
P +
+
+
+
+
+
( ) ( ) .
.
4
=
2
=
2
3
2
3
2
= 4
2
2
2
2
t
t
t
t
t +
+
+
( ) ( ) .
4
=
4
2
t
t
Q
P +
( )( ) ( ) ( ) ( ) ( )
t
Q
t
Q
t
P
t
P
t
Q
PQ
P
2
2
2
2
2
=
2 +
+
+
+
( ) ( )( ) ( )2
2
2
2
2
3
2
2
3
2
3
2
2
3
2
= t
t
t
t
t
t +
+
+
+
+
+
( )
3
2
2
2
3
2
4
2
6
9
6
4
6
4
2
12
9
4
12
8
12
4
9
4
= t
t
t
t
t
t
t
t
t
t
t
t +
+
+
+
+
+
+
+
+
( ) ( ) ( )( ),
2
=
4
=
2
2
4
2
t
Q
PQ
P
t
4
=
4
t
t
Q
P +
+
+
( ) .
2
=
2
2
2
Q
PQ
P
Q
P +
+
+](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-126-320.jpg)

![239
Diversidad funcional
en el aula
Al trabajar en equipo puede existir integrantes
con muy poca autoestima por ello es necesario
reconocer las fortalezas y motivarloa continuar
con el trabajo.
Trabajo colaborativo
Trabajen en equipo, indaguen y resuelvan.
Calcula P (a + h) – P(a)
h
para a, hR
con h ≠ 0. Este cociente se llama cociente
incremental y está bien definido en R.
5
a) P(x) = 3 + 5x, xR.
b) P(x) = 2 + 5x + x2
, xR.
c) P(x) = 2 + 10x + 3x2
+ 15x3
, xR.
a)
P(t) = 0,
Q(t) = t,
R(t) = – 2 –t,
tR.
b)
P(t) = 22 + 7t – t3
,
Q(t) = 11t2
– 7t3
,
R(t) = 12 – 8t2
+ 4t4
,
tR.
c)
P(t) = 8t6
– 4t4
+ 2t2
– 6,
Q(t) = 5t + 11t5
,
R(t) = t6
– 2t5
+ 4t4
,
tR.
Halla los polinomio siguientes:
PQ, PR, PQR, P(Q + R), P(Q – R), P(– Q – R).
6
Sea el polinomio de [ ]
k R dado en cada
caso. Calculen P2
, P3
y P4
.
7
a) P(t) = –3.
b) P(t) = 2t.
c) P(t) = 5t3
.
d) P(t) = 8 – 2t.
e) P(t) = 3t2
– 8t.
f) P(t) = 2t5
– 11.
g) P(t) = –3t4
+ t3
.
Demuestren las siguientes propiedades.
Para todo P, Q, R [ ]
k R .
8
a) PQ = QP.
b) 1P = P.
c) P(–Q) = (–P)Q = –PQ.
d) P(Q – R) = PQ – PR.
a) (P + Q) (P – Q) = P2
– Q2
.
b) (P – Q)2
= P2
– 2PQ + Q2
.
c) (P + Q)2
– (P – Q)2
= 4PQ.
d) (P + Q)2
+ (P – Q)2
= 2(P2
+ Q2
).
e) (P + Q)3
= P3
+ 3P2
Q + 3PQ2
+ Q3
.
f) (P – Q)3
= P3
– 3P2
Q + 3PQ2
– Q3
.
Sean P, Q los polinomios definidos por
9
P(t) = 2 + 3t,
Q(t) = t – 5t2
.
tR. Verifiquen:
Archivo editorial, (2020).](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-128-320.jpg)
![240
Solución de problemas
cotidianos
Modelo simple de cálculo de las ecuaciones
de las mediatrices
1. Para mejorar la circulación vehicular en una ciu-
dad, se quiere construir un redondel. Para ello, se
ha diseñado un triángulo que pasa por los puntos
A
B
C
= (1, 1),
A
B
C
= (–3, 2) y
A
B
C = (– 1, 4). Se piensa
construir este redondel de tal manera que pase
por los vértices del triángulo y, adicionalmente,
en el centro se colocará una estatua del alcalde,
en reconocimiento a su labor. ¿En qué coordena-
das se debe levantar la estatua?
a) Realiza un gráfico de la situación.
Cálculo de las medianas
2. Sean A B C
(2,3); (6,9); (8,1)
= = = los vérti-
ces de un triángulo. Determina las ecuaciones
de las medianas y su punto de intersección.
Recuerda que este punto se llama baricentro.
Cálculo de las alturas
3. En el triángulo del ejercicio anterior, determi-
na las ecuaciones de las alturas y su punto de
intersección. Recuerda que este punto se de-
nomina ortocentro.
4. Halla la ecuación de la recta que pasa por
x y
P
1 3
2
1;
1 2
2
3
2
,
( 1,
3
2
).
1
=
−
=− =
+
=
= −
= (–1, 2) y es paralela a la recta 3x – y + 4 = 0.
Para solucionar el problema, debemos calcular
las ecuaciones de las mediatrices de los lados del
triángulo y luego debemos buscar el punto de
intersección que nos dará el centro de la circunfe-
rencia circunscrita al triángulo.
b) Completa el proceso de resolución.
Recuerda que la mediatriz es el segmento de
recta que sale perpendicular desde el punto
medio del lado del triángulo.
* Calcula los puntos medios.
Punto medio de [A, B].
x y
P
1 3
2
1;
1 2
2
3
2
,
( 1,
3
2
).
1
=
−
=− =
+
=
= −
Punto medio de
A
B
C
A
B
C
, .
1
2
3
4
1
–1
–2
–3 0
0
A
B
C
y
x
p Figura 5.15.
*Calcula la pendiente de cada lado del triángulo.
Pendientes: mAB, mBC, mAC.
=
−
+
=
−
1 2
1 3
1
4
mAB .
* Determina las ecuaciones de las mediatrices.
Para ello, toma el punto medio y la pendiente in-
vertida y con signo contrario.
P1
= (–1, 3/2); m1
= 4.
y x
x y
4( 1).
8 2 11 0.
3
2
− = +
+ + =
* Toma dos ecuaciones de las mediatrices y
resuelve el sistema. El punto de intersección
son las coordenadas donde debe levantarse el
monumento.
Practica en tu cuaderno
Punto medio de
A
B
C
A
B
C
, .](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-129-320.jpg)









![250
DCCD:M.5.1.40. Aplicar las operaciones entre polinomios de grados ≤ 4, esquema de Hörner, teorema del residuo y sus respectivas propiedades para
factorizar polinomios de grados ≤ 4 y reescribir los polinomios.
División de polinomios. Teorema
del residuo
La división de números enteros tiene una estrecha analogía con la
división de polinomios que se describe a continuación.
Sean p, q dos polinomios reales no nulos, esto es, p, q []; se trata
de un proceso que permite encontrar c, r [], con grado del po-
linomio r menor que el grado del polinomio q, tal que
p(x) = c(x)q(x) + r(x), ∀x .
La p se llama dividendo, q se llama divisor, c se llama cociente, r se
llama residuo. Se prueba que dados p, q [], siempre se pueden
hallar los polinomios c y r que satisfacen la condición anterior. Cuando
r(x) = 0, ∀x , decimos que el polinomio q divide al polinomio p,
y escribimos
p
q
= c, o también,
p(x)
q(x)
= c(x), ∀x , siempre que q(x) ≠ 0.
Si p, q son dos polinomios reales no nulos, tal que grad(p) grad(q),
entonces p = 0 × q + r, con el cociente c = 0, residuo r = p.
Ejercicios resueltos
1. Sean p, c, q los polinomios definidos como
p(x) = (2x – 3)(4x + 5),
c(x) = 2x – 3,
q(x) = 4x + 5,
∀x .
Entonces,
p(x) = c(x)q(x) + r(x), ∀x ,
es decir que q divide a p, siendo c el cociente, y r(x) = 0, ∀x
el residuo. Luego,
p x
q x
x x
x
x c x x
( )
( )
=
(2 3)(4 5)
4 5
=2 3= ( ),
5
4
.
− +
+
− ∀ ∈ −
5
4
– .
2. Sean p, c, q los polinomios definidos como
p(x) = (x2
+ 1)(x + 10) + 2,
c(x) = x + 10,
q(x) = x2
+ 1,
r(x) = 2,
∀x .
Entonces,
p(x) = c(x)q(x) + r(x), ∀x .
La división de p para q tiene como cociente c, y residuo r, siendo
el grado de r menor que el grado de q. Luego,
p x
q x
x
x
x
( )
( )
= 10
2
1
, .
2
+ +
+
∀ ∈
Saberes previos
¿Qué significa que el
grado de un polinomio sea ≤ 4?
¿Cuál es el opuesto aditivo de
un polinomio? ¿Cuándo dos
polinomios son iguales?
Desequilibrio cognitivo
¿Qué funciones im-
portantes se aproximan con
polinomios?
Recuerda que…
Al realizar la división de 35
para 8, se obtiene por cociente 4
y residuo 3, que se escribe
35 = 4 × 8 + 3, o en forma
equivalente,
35
8
= 4 +
3
8
.
De manera similar, si dividimos 32
para 8, se obtiene por cociente 4 y
residuo 0. Así
32 = 4 × 8
32
8
= 4.
En este caso decimos que 8 divide
a 32. De manera general, dados
dos números enteros positivos a,
b con a ≥ b, al realizar la división
de a para b se obtiene el cociente
cZ
+
y un residuo rZ
+
, de
modo que 0 ≤ r b,
a
b
= c +
r
b
a = cb + r.
El número entero a se llama
dividendo y b, se llama divisor.
Cuando r = 0, se dice que b divide
a.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-139-320.jpg)
![251
3. Sean p, q [] no nulos, dados como
+ + + + ∀ ∈
+ + + +
+ + + +
+ + + + ∀ ∈
+ + + ∀ ∈
∀ ∈
+ ∀ ∈
, ,
{ }
;
p t a a t a t a t a t t
p t
q t
a a t a t a t a t
at
a
at
a t
at
a t
at
a t
at
a t
at
a
at
a
a
a
a
t
a
at
t
a
a
t t
c t
a
a
a
a
t
a
at
t
a
a
t t
r t a t
p t c t q t r t t
( ) =
( )
( )
=
=
= , 0 .
( ) = ,
( ) = , .
( ) = ( ) ( ) ( ), .
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2 3 2 4 3
1 2 3 2 4 3
0
con a4
≠ 0, de modo
que grad(p) = 4; q(t) = at, ∀x , siendo a ≠ 0, con lo que
grad(q) = 1. La división de un polinomio p para un monomio
como q se encuentra fácilmente. Observa
+ + + + ∀ ∈
+ + + +
+ + + +
+ + + + ∀ ∈
+ + + ∀ ∈
∀ ∈
+ ∀ ∈
, ,
{ }
;
p t a a t a t a t a t t
p t
q t
a a t a t a t a t
at
a
at
a t
at
a t
at
a t
at
a t
at
a
at
a
a
a
a
t
a
at
t
a
a
t t
c t
a
a
a
a
t
a
at
t
a
a
t t
r t a t
p t c t q t r t t
( ) =
( )
( )
=
=
= , 0 .
( ) = ,
( ) = , .
( ) = ( ) ( ) ( ), .
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2 3 2 4 3
1 2 3 2 4 3
0
Claramente, el cociente c es el polinomio de grado 3:
+ + + + ∀ ∈
+ + + +
+ + + +
+ + + + ∀ ∈
+ + + ∀ ∈
∀ ∈
+ ∀ ∈
, ,
{ }
;
p t a a t a t a t a t t
p t
q t
a a t a t a t a t
at
a
at
a t
at
a t
at
a t
at
a t
at
a
at
a
a
a
a
t
a
at
t
a
a
t t
c t
a
a
a
a
t
a
at
t
a
a
t t
r t a t
p t c t q t r t t
( ) =
( )
( )
=
=
= , 0 .
( ) = ,
( ) = , .
( ) = ( ) ( ) ( ), .
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2 3 2 4 3
1 2 3 2 4 3
0
y el residuo r es el polinomio de grado 0:
+ + + + ∀ ∈
+ + + +
+ + + +
+ + + + ∀ ∈
+ + + ∀ ∈
∀ ∈
+ ∀ ∈
, ,
{ }
;
p t a a t a t a t a t t
p t
q t
a a t a t a t a t
at
a
at
a t
at
a t
at
a t
at
a t
at
a
at
a
a
a
a
t
a
at
t
a
a
t t
c t
a
a
a
a
t
a
at
t
a
a
t t
r t a t
p t c t q t r t t
( ) =
( )
( )
=
=
= , 0 .
( ) = ,
( ) = , .
( ) = ( ) ( ) ( ), .
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2 3 2 4 3
1 2 3 2 4 3
0
De modo que
+ + + + ∀ ∈
+ + + +
+ + + +
+ + + + ∀ ∈
+ + + ∀ ∈
∀ ∈
+ ∀ ∈
, ,
{ }
;
p t a a t a t a t a t t
p t
q t
a a t a t a t a t
at
a
at
a t
at
a t
at
a t
at
a t
at
a
at
a
a
a
a
t
a
at
t
a
a
t t
c t
a
a
a
a
t
a
at
t
a
a
t t
r t a t
p t c t q t r t t
( ) =
( )
( )
=
=
= , 0 .
( ) = ,
( ) = , .
( ) = ( ) ( ) ( ), .
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2
2
3
3
4
4
0 1 2 3 2 4 3
1 2 3 2 4 3
0
4. Sean
p(x) = 6x2
+ 17x + 9, ∀x ,
q(x) = 2x + 1, ∀x .
Procedemos a dividir el polinomio p para q. Empezamos con en-
contrar un monomio w que se obtiene dividiendo el término de
grado más alto del polinomio p para el término de grado más alto
del polinomio q, esto es,
w x
x
x
x x
p x w x q x R x
R x p x w x q x
x x x x
x
w x
x
x
x
( )=
6
2
=3 , {0}.
( )= ( ) ( ) ( ),
( )= ( ) ( ) ( )
=6 17 9 3 (2 1)
=14 9.
( )=
14
2
=7, {0}.
2
1
1
2
1
∀ ∈
+
−
+ + − +
+
∀ ∈
Entonces,
w x
x
x
x x
p x w x q x R x
R x p x w x q x
x x x x
x
w x
x
x
x
( )=
6
2
=3 , {0}.
( )= ( ) ( ) ( ),
( )= ( ) ( ) ( )
=6 17 9 3 (2 1)
=14 9.
( )=
14
2
=7, {0}.
2
1
1
2
1
∀ ∈
+
−
+ + − +
+
∀ ∈
de donde R1
se obtiene como
w x
x
x
x x
p x w x q x R x
R x p x w x q x
x x x x
x
w x
x
x
x
( )=
6
2
=3 , {0}.
( )= ( ) ( ) ( ),
( )= ( ) ( ) ( )
=6 17 9 3 (2 1)
=14 9.
( )=
14
2
=7, {0}.
2
1
1
2
1
∀ ∈
+
−
+ + − +
+
∀ ∈
Como el grado de R1
coincide con el de q, el proceso de división
continúa. Se divide el término de más alto grado de R1
para el tér-
mino de más alto grado de q:
w x
x
x
x x
p x w x q x R x
R x p x w x q x
x x x x
x
w x
x
x
x
( )=
6
2
=3 , {0}.
( )= ( ) ( ) ( ),
( )= ( ) ( ) ( )
=6 17 9 3 (2 1)
=14 9.
( )=
14
2
=7, {0}.
2
1
1
2
1
∀ ∈
+
−
+ + − +
+
∀ ∈
Luego, R x w x q x R x
R x R x w x q x
x x
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x
c x x
( ) = ( ) ( ) ( ),
( ) = ( ) ( ) ( )
=14 9 7(2 1) =2.
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(3 7)(2 1) 2.
( ) =3 7,
1 1 2
2 1 1
1
1 2
1 2
+
−
+ − +
+
+ +
+ +
+ + +
+
y de esta igualdad obtenemos R2
:
R x w x q x R x
R x R x w x q x
x x
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x
c x x
( ) = ( ) ( ) ( ),
( ) = ( ) ( ) ( )
=14 9 7(2 1) =2.
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(3 7)(2 1) 2.
( ) =3 7,
1 1 2
2 1 1
1
1 2
1 2
+
−
+ − +
+
+ +
+ +
+ + +
+
El grado de R2
es menor que el grado de q. El proceso concluye. Así:
R x w x q x R x
R x R x w x q x
x x
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x
c x x
( ) = ( ) ( ) ( ),
( ) = ( ) ( ) ( )
=14 9 7(2 1) =2.
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(3 7)(2 1) 2.
( ) =3 7,
1 1 2
2 1 1
1
1 2
1 2
+
−
+ − +
+
+ +
+ +
+ + +
+
Elcocientecestádefinidocomo
R x w x q x R x
R x R x w x q x
x x
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x
c x x
( ) = ( ) ( ) ( ),
( ) = ( ) ( ) ( )
=14 9 7(2 1) =2.
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(3 7)(2 1) 2.
( ) =3 7,
1 1 2
2 1 1
1
1 2
1 2
+
−
+ − +
+
+ +
+ +
+ + +
+ yelresiduoresr(x)=2.
Recuerda que…
Dados los polinomios p, q:
p(t) = a0
+ a1
t + a2
t2
+ a3
t3
+ a4
t4
,
q(t) = at3
, ∀t .
Se tiene grad(q) = 3;
La división de p para q se realiza
como sigue:
p t
q t
a a t a t a t a t
at
a a t a t
at
a t
at
a t
at
a a t a t
at
a
a
a
a
t
t
( )
( )
=
=
= ,
{0}.
0 1 2
2
3
3
4
4
3
0 1 2
2
3
3
3
3
4
4
3
0 1 2
2
3
3 4
+ + + +
+ +
+ +
+ +
+ +
∀ ∈
El cociente c es el polinomio de
grado 1:
( ) ( ) ( )
+ ∀ ∈
+ + ∀ ∈
+ ∀ ∈
,
.
, .
c t
a
a
a
a
t t
r t a a t a t t
p t c t q t r t t
( ) = ,
( ) = ,
( ) =
3 4
0 1 2
2
y el residuo r es es el polinomio
de grado 2:
( ) ( ) ( )
+ ∀ ∈
+ + ∀ ∈
+ ∀ ∈
,
.
, .
c t
a
a
a
a
t t
r t a a t a t t
p t c t q t r t t
( ) = ,
( ) = ,
( ) =
3 4
0 1 2
2
Nota que el grado del polino-
mio r es menor que el grado de
q. Así,
( ) ( ) ( )
+ ∀ ∈
+ + ∀ ∈
+ ∀ ∈
,
.
, .
c t
a
a
a
a
t t
r t a a t a t t
p t c t q t r t t
( ) = ,
( ) = ,
( ) =
3 4
0 1 2
2](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-140-320.jpg)
![252
Interdisciplinariedad
Matemática y el
mercado de valores
Los polinomios también
pueden utilizarse para modelar
situaciones diferentes, como
en el mercado de valores para
prever cómo pueden variar los
valores con el tiempo.
Las personas de negocios
también utilizan polinomios
para modelar mercados, por
ejemplo, para advertir cómo el
aumento del precio de un bien
afectará sus ventas.
Los polinomios son utilizados
para aproximar valores de
funciones trigonométricas
como sen(x), cos(x) o valores de
la función exponencial ex
, entre
otras funciones.
Los polinomios son la base para
el diseño de algoritmos que,
a su vez, sirven para el diseño
electrónico de calculadoras
científicas.
Shutterstock,
(2020).
515002651
5. Sean p, q los polinomios definidos como
p x x x x x x
q x x x x
( )=20 10 59 21 37, ,
( )=4 2 3, .
4 3 2
2
− + − + ∀ ∈
− + ∀ ∈
Realiza la división de p para q y halla el cociente c y el residuo r.
Divide el término de más alto grado de p para el término de más
alto grado de q:
w x
x
x
x x
p x w x q x R x x
R x p x w x q x
x x x x x x x
x x
( ) =
20
4
=5 , 0,
( ) = ( ) ( ) ( ), ,
( ) = ( ) ( ) ( )
=20 10 59 21 37 5 (4 2 3)
= 44 21 37.
1
4
2
2
1 1
1 1
4 3 2 2 2
2
≠
+ ∀ ∈
−
− + − + − − +
− +
de donde:
w x
x
x
x x
p x w x q x R x x
R x p x w x q x
x x x x x x x
x x
( ) =
20
4
=5 , 0,
( ) = ( ) ( ) ( ), ,
( ) = ( ) ( ) ( )
=20 10 59 21 37 5 (4 2 3)
= 44 21 37.
1
4
2
2
1 1
1 1
4 3 2 2 2
2
≠
+ ∀ ∈
−
− + − + − − +
− +
w x
x
x
x x
p x w x q x R x x
R x p x w x q x
x x x x x x x
x x
( ) =
20
4
=5 , 0,
( ) = ( ) ( ) ( ), ,
( ) = ( ) ( ) ( )
=20 10 59 21 37 5 (4 2 3)
= 44 21 37.
1
4
2
2
1 1
1 1
4 3 2 2 2
2
≠
+ ∀ ∈
−
− + − + − − +
− +
Como grad(R1
) = grad(q) = 2, se divide el término de más alto
grado de R1
para el término de más alto grado de q:
≠
+ ∀ ∈
−
− + − − +
+ ∀ ∈
( ) =
44
4
=11, 0,
( ) = ( ) ( ) ( ), .
( ) = ( ) ( ) ( )
= 44 21 37 11(4 2 3)
= 4, .
2
2
2
1 2 2
2 1 2
2 2
w x
x
x
x
R x w x q x R x x
R x R x w x q x
x x x x
x x
Luego,
≠
+ ∀ ∈
−
− + − − +
+ ∀ ∈
( ) =
44
4
=11, 0,
( ) = ( ) ( ) ( ), .
( ) = ( ) ( ) ( )
= 44 21 37 11(4 2 3)
= 4, .
2
2
2
1 2 2
2 1 2
2 2
w x
x
x
x
R x w x q x R x x
R x R x w x q x
x x x x
x x
≠
+ ∀ ∈
−
− + − − +
+ ∀ ∈
( ) =
44
4
=11, 0,
( ) = ( ) ( ) ( ), .
( ) = ( ) ( ) ( )
= 44 21 37 11(4 2 3)
= 4, .
2
2
2
1 2 2
2 1 2
2 2
w x
x
x
x
R x w x q x R x x
R x R x w x q x
x x x x
x x
Como 1 = grad(R2
) grad(q) = 2, el proceso concluye. Resulta
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x x x x
c x x x r x x x
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(5 11)(4 2 3) 4, .
( ) =5 11, , ( ) = 4, .
1 1
1 2 2
1 2 2
2 2
2
+
+ +
+ +
+ − + + + ∀ ∈
+ ∀ ∈ + ∀ ∈
Así, el cociente y el residuo son los polinomios definidos como
p x w x q x R x
w x q x w x q x R x
w x w x q x R x
x x x x x
c x x x r x x x
( ) = ( ) ( ) ( )
= ( ) ( ) ( ) ( ) ( )
=( ( ) ( )) ( ) ( )
=(5 11)(4 2 3) 4, .
( ) =5 11, , ( ) = 4, .
1 1
1 2 2
1 2 2
2 2
2
+
+ +
+ +
+ − + + + ∀ ∈
+ ∀ ∈ + ∀ ∈
Teorema del residuo
Sea p un polinomio de grado mayor o igual que 1 y q(x) = x – a,
donde a R.
De acuerdo con proceso de la división, se tiene
+
− + ∀ ∈
− +
× +
− + ∀ ∈
( ) = ( ) ( ) ( )
= ( )( ) ( ), ,
( ) = ( )( ) ( )
= ( ) 0 ( ) = ( ).
( ) = ( )( ) ( ), .
p x c x q x r x
c x x a r x x
p a c a a a r a
c a r a r a
p x c x x a p a x
siendo c(x) el cociente y r(x) el residuo. Entonces,
+
− + ∀ ∈
− +
× +
− + ∀ ∈
( ) = ( ) ( ) ( )
= ( )( ) ( ), ,
( ) = ( )( ) ( )
= ( ) 0 ( ) = ( ).
( ) = ( )( ) ( ), .
p x c x q x r x
c x x a r x x
p a c a a a r a
c a r a r a
p x c x x a p a x
En consecuencia,
+
− + ∀ ∈
− +
× +
− + ∀ ∈
( ) = ( ) ( ) ( )
= ( )( ) ( ), ,
( ) = ( )( ) ( )
= ( ) 0 ( ) = ( ).
( ) = ( )( ) ( ), .
p x c x q x r x
c x x a r x x
p a c a a a r a
c a r a r a
p x c x x a p a x
Este resultado se conoce como teorema del residuo.
Recuerda que…
Teorema del residuo
Sean p [] con grad(p) ≥ 1,
a , q(x) = x – a, ∀x R.
El residuo de la división de p
para q está dado como p(a),
esto es,
p(x) = c(x)(x – a) + p(a), ∀x R.
p Hombre de negocios.](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-141-320.jpg)
![253
Sean p [] con grad(p) ≥ 1, a . Cuando p(a) = 0, se dice que
a es raíz de la ecuación p(x) = 0.
En la tabla siguiente se muestra el grado del polinomio y el número
de raíces reales.
Grado del polinomio p Número de raíces reales
1 1
2 0, 2
3 1, 3
4 0, 2, 4
5 1, 3, 5
Por ejemplo, p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
no tiene raíces reales; mientras que
p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
con
p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
tiene dos raíces
reales,a x = a, x = b.
Ejercicios resueltos
1. Sean
p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
Apliquemos el teorema del residuo. Por el esquema de Hörner,
p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
Luego,
p x x x
p x k x a x b x
k a b k
p x x x x x
q x x x
p x x x x x
p
p x x x x
( ) = 1, ,
( ) = ( )( ), ,
, , , 0,
( ) = 5 7, .
( ) = 5, .
( ) =7 (1 (5 )), ,
( 5) =7 ( 5)(1 ( 5)(5 5)) =7.
( ) =( 5)( 1) 7, .
2
3 2
2
+ ∀ ∈
− + ∀ ∈
∈ ≠
+ + + ∀ ∈
+ ∀ ∈
+ + + ∀ ∈
− + − + − −
+ + + ∀ ∈
2. Sean
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
Factoriza p. Por el teorema del residuo, se tiene p(–6) = 0, es decir,
el residuo r(x) = 0; con lo que a = –6 es raíz de la ecuación
p(x) = 0. En consecuencia, x + 6 divide a p(x); luego,
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
Nota que el cociente es
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
con a, b por de-
terminarse. Por la definición de igualdad de polinomios, se obtiene
a = 1, b = –6. Así,
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
Para completar el proceso de factorización, resolvemos la ecua-
ción de segundo grado:
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
x1
= –3, x2
= 2 son las raíces de esta ecuación.
Los polinomios
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
dividen a p. Por lo tanto,
p x x x x
q x x x
p x x x ax b
x a x b a x b x
c x x ax b
p x x x x x
x x x
q x x q x x
p x x x x x
( ) = 7 36, .
( ) = 6, .
( ) =( 6)( )
= ( 6) ( 6 ) 6 , .
( ) = ,
( ) =( 6)( 6), .
6 = 0, =
1 1 24
2
=
1 5
2
,
( ) = 3, ( ) = 2,
( ) =( 6)( 3)( 2), .
3 2
2
3 2
2
2
2
1 2
+ − ∀ ∈
+ ∀ ∈
+ + +
+ + + + + ∀ ∈
+ +
+ + − ∀ ∈
+ −
− ± + − ±
+ −
+ + − ∀ ∈
Recuerda que…
Del teorema del residuo,
se desprende el siguiente resul-
tado: a es raíz de la ecuación
p(x) = 0 si y solo si p(x) es
divisible por x – a. En tal caso, el
polinomio p se factoriza como
p(x) = (x – a)c(x),
siendo c(x) el cociente, r(x) = 0
el residuo. Si c(x) es divisible por
x – b con b R, entonces
c(x) = (x – b)c1
(x),
p(x) = (x – a)(x – b)c1
(x), t R.
Si grad(c1
) ≥ 1, el proceso
continúa.
Glosario
polinomio. Expresión
algebraica que constituye la
suma o la resta ordenadas de
un número finito de términos o
monomios.
teorema. Proposición mate-
mática demostrable a partir de
axiomas o de proposiciones ya
demostradas.
a
cb](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-142-320.jpg)



![257
Conversión de binario a decimal y viceversa
Sea A = (an
an–1
... a0
)2
un número binario. Para convertir el número A
al sistema decimal, lo asociamos al polinomio
+ + + + ∀ ∈
P x a a x a x a x x
n
n
( ) = , ,
0 1 2
2
y evaluamos P(2), usando el esquema de Hörner. Así, A = P(2).
Veamos el problema recíproco.
Sea M N con M ≠ 0 en base 10. Supongamos que M tiene la
siguiente representación en binario: M = (an
an–1
... a2
a1
a0
)2
, cuyo poli-
nomio asociado en x = 2 es
P a a a a M
n
n
(2) = 2 2 2 = .
0 1 2
2
+ × + × + + ×
Para determinar las cifras binarias a0
, a1
, ..., an
, procedemos como
sigue: el número a a an
n
2 2 2
1 2
2
× + × + + × es par.
Entonces, {M a
M a
impar si y solo si =1,
par si y solo si = 0.
0
0
Determinada la cifra a0
,
pasamos a determinar la cifra a1
. Definimos
M
M a
a a an
n
=
2
= 2 2 .
1
0
1 2
1
−
+ × + + × −
Luego, {M a
M a
impar si y solo si =1,
par si y solo si = 0.
1 1
1 1
De manera análoga,
M
M a
a a an
n
=
2
= 2 2 ,
2
1 1
2 3
2
−
+ × + + × −
entonces, {M a
M a
impar si y solo si =1,
par si y solo si = 0.
2 2
2 2
Continuando con este proceso
n veces, obtenemos las cifras binarias ak
, k = 0,1, ..., n.
Queda por determinar el número n que corresponde a las n + 1 cifras
binarias. Para ello, notemos que dado M N, existe n N, tal que
2n
≤ M 2n+1
.
Recordemos que N = [0] ∪ [1], con [0], [1] las clases residuales mó-
dulo 2: [0] = {2n | n N} es el conjunto de números naturales pares,
[1] = {2m + 1 | m N} es el conjunto de los números naturales im-
pares. El procedimiento anterior equivale a utilizar el algoritmo de la
división de Euclides: a = 2c + r, con c N y r = 0 o 1. Luego, Mk
[r],
entonces, ak
= r, k = 0,1, ..., n.
Ejercicios resueltos
1. Sea M = 2 412. Puesto que 211
= 2 048 ≤ M 212
= 4 096, se sigue
que n = 11. Luego, 2 412 = (a11
a10
...a1
a0
)2
. Determinamos las cifras
binarias a0
, a1
, ..., a11
.
Recuerda que…
El procedimiento
descrito para obtener las cifras
binarias de un número en base
10 puede extenderse fácilmente
a otras bases. Debe tenerse pre-
sente el algoritmo de Euclides:
dados M en el sistema decimal
y N la nueva base, existen
c, r N con 0 ≤ r N, tal
que M = r + cN, donde c es el
cociente y r el residuo.
Simbología matemática
Denotamos un número
binario por A = (an
an–1
... a0
)2
.
Por lo tanto, 2 412 = (100101101100)2
.
i 0 1 2 3 4 5 6 7 8 9 10 11
Mi 2 412 1 206 603 301 150 75 37 18 9 4 2 1
ai
0 0 1 1 0 1 1 0 1 0 0 1
Archivo editorial, (2020).
Glosario
algoritmo. Conjunto
ordenado de operaciones siste-
máticas que permite hacer un
cálculo y hallar la solución de un
tipo de problemas.
binaria. Que está compuesto de
dos elementos.
a
cb](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-146-320.jpg)
![Taller práctico
258
Consideremos el número M = 2 380 y N = 5.
Como 54 = 625 y 55 = 3 125,
entonces 54
≤ 2 380 55
, con lo cual
2 380 = (a4
a3
a2
a1
a0
)5
donde
ai
{0, 1, 2, 3, 4}, i = 0, 1, 2, 3, 4.
Las clases residuales módulo 5 son [0], [1], [2],
[3], [4], donde [r] = {5m + r| m N} con r = 0,
1, 2, 3, 4. Se tiene
a a a a a
2 380 = 5 5 5 5 .
0 1 2
2
3
3
4
4
+ × + × + × + ×
M = 2 380 [0]. Entonces, a0
= 0,
M
M a
a a a a
=
5
=
2380 0
5
=476 = 5 5 5 ,
1
0
1 2 3
2
4
3
− −
+ × + × + ×
M1
= 476 [1]. Entonces, a1
= 1,
M
M a
a a a
=
5
=
476 1
5
= 95 = 5 5 ,
2
1 1
2 3 4
2
− −
+ × + ×
M2
= 95 [0]. Entonces, a2
= 0,
M
M a
a a
=
5
=
95 0
5
=19 = 5,
3
2 2
3 4
− −
+ ×
M3
= 19 [4]. Entonces, a3
= 4,
M
M a
a
=
5
=
19 4
5
=3 = .
4
3 3
4
− −
Luego, 2 380 = (_________)5
.
DCCD: M.5.1.41. Resolver aplicaciones de los polino-
mios de grados ≤4 en la informática (sistemas de nume-
ración, conversión de sistema de numeración binario a
decimal y viceversa) en la solución de problemas.
Completa la solución de este ejercicio.
Completa la solución de este ejercicio.
1
2
Representa en base 10 los siguientes
números:
3
a) (4 746)8
. b) (74 128)9
.
c) (864 568)16
. d) (10 000)3
.
Sea M = 35 Primero, determinemos el número
n. Puesto que 32 = 25
, 64 = 26
y 25
≤ 35 26
, se
tiene que n = 5. Por lo tanto, debemos determi-
nar 6 cifras binarias a0
, a1
, ..., a5
. Ponemos
M = 35 = (a5
a4
a3
a2
a1
a0
)2
. Entonces,
a a a a a a
35= 2 2 2 2 2 .
0 1 2
2
3
3
4
4
5
5
+ × + × + × + × + ×
Como 35 es impar, resulta que a0
= 1. Luego,
+ + × + × + × + ×
35 =1 2( 2 2 2 2 ),
1 2 3
2
4
3
5
4
a a a a a
de donde
M a a a a a
=
35 1
2
=17= 2 2 2 2 ,
1 1 2 3
2
4
3
5
4
−
+ × + × + × + ×
M1
es impar. Entonces, a1
= 1. Se tiene
a a a a
17 =1 2( 2 2 2 ),
2 3 4
2
5
3
+ + × + × + ×
M a a a a
=
17 1
2
=8 = 2 2 2 ,
2 2 3 4
2
5
3
−
+ × + × + ×
M2
es par. Entonces, a2
= 0 y
+ + × + ×
−
+ × + ×
8 = 0 2( 2 2 ),
=
8 0
2
= 4 = 2 2 ,
3 4 5
2
3 3 4 5
2
a a a
M a a a
M3
es par. Entonces, a3
= 0 y
M a a
=
4 0
2
=2 = 2.
4 4 5
−
+ ×
M4
es par. Entonces, a4
= 0.
Luego, M a
2 0
2
___
5 5
−
= =
a5
= _________
Recolectando todas las cifras, tenemos que
35 = (_________)2
.
En la siguiente tabla se ilustra todo el procedi-
miento descrito para determinar las cifras bina-
rias. Complétala.
i 0 1 2 3 4 5
Mi 35 17 8 4 2 1
ai
1 1 0
Nota que M2
, M3
, M4
, [0], M, M1
, M5
, [1].](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-147-320.jpg)
![259
Trabajo colaborativo
Sea m = 35 y N = 3.
6
Trabajen en equipo y resuelvan.
En cada caso, representa, en la base N
que se indica, el número M = 280 en base
10.
4
En los siguientes ejercicios, representa
en la base N los números en base 10.
5
a) N = 2. b) N = 3.
c) N = 4. d) N = 8.
e) N = 16.
a) 314, N = 2. b) 27 182, N = 4.
c) 5 234, N = 7. d) 1 786, N = 8.
e) 1 955, N = 5. f) 13 526, N = 6.
g) 1354, N = 2. h) 48 357, N = 2.
e) (14 142)5
. f) (111 100 011)2
.
g) (3 120 132)4
. h) (6 543 210)7
.
a) Observen que: 33 = 27 y 34 = 81, entonces
33
≤ 35 34
, luego, n = 3.
b) Determinen a0
, a1
, a2
, a3
, cifras en base 3.
Esto es, ai
{0, 1, 2}, i = 0, 1, 2, 3.
Noten que N = [0] ∪ [1]∪[2], siendo [r] =
{3m + r | m N} la clase residual módulo 3,
con r = 0, 1, 2.
c) Pongan 35 = (a3
a2
a1
a0
)3
.
d) Entonces, verifiquen.
M = 35 = a0
+ a1
× 3 + a2
× 32
+ a3
× 33
= a0
+ 3(a1
+ a2
× 3 + a3
× 32
).
e) Continúen desarrollando el proceso para
escribir el número 35 en base 3.
Diversidad funcional
en el aula
Cuando existe un compañero con discapacidad
visual es necesario utilizar escritura macrotipo
o braille.
Archivo editorial, (2020).](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-148-320.jpg)

![261
El dato procesado de consumo energético proporcionado por las auto-
ridades de la provincia XYZW, en el año 2015, es 207 vatios/persona y,
en el mes de julio de 2016, se reporta un consumo de 221,4 vatios/per-
sona. Aplicando la función polinomial, se obtiene p(2016,5) = 229,550
625. Los resultados obtenidos con la función polinomial construida
muestran satisfactoriamente la tendencia de crecimiento de consumo
de electricidad en la provincia XYZW. Es así que en 8 años se espera
duplicar el consumo de electricidad del estimado en el año 2010, lo que
debe reflejar mejores condiciones de vida de su población.
Modelo 2. Mi cantante favorito
Mi cantante favorito/a promociona su nuevo éxito, lo que sacude
las redes sociales. En las primeras 36 horas, se registra el número de
visitas, que se muestran en la Tabla 2.
Dada la información de la que se dispone, los promotores están in-
teresados en conocer la evolución de las visitas en las primeras cien
horas. Quieren saber si en este tiempo se supera el millón de visitas.
Para el efecto, se propone modelar con polinomios de grado ≤ 4 de
la forma
v t c c t c t c t c t
( ) = ,
0 1 2
2
3
3
4
4
+ + + +
siendo t R, c0
, c1
, c2
, c3
, c4
constantes reales (son las incógnitas), que
deben obtenerse de la información suministrada en la Tabla.
i. La variable independiente t representa el tiempo. Introducimos,
entonces, la restricción t ≥ 0. Puesto que al instante t = 0 no se tie-
nen visitas, entonces, c0
= 0, y la función polinomial tiene la forma
v t c t c t c t c t t
( ) = , 0.
1 2
2
3
3
4
4
+ + + ≥
ii. De la definición de esta función y de los datos de la Tabla, se tiene
v c c c c
v c c c c
v c c c c
p c c c c
60 = (4) = 4 16 64 256 ,
930 = (10) =10 100 1 000 10 000 ,
5 562 = (18) =18 324 5 832 104 976 ,
45 468 = (36) =36 1296 46 656 1 679 616 .
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
+ + +
+ + +
+ + +
+ + +
iii. Este sistema de ecuaciones se reduce al siguiente:
v c c c c
v c c c c
v c c c c
p c c c c
15 = (4) = 4 16 64 ,
93 = (10) = 10 100 1 000 ,
309 = (18) = 18 324 5 832 ,
1263 = (36) = 36 1296 46 656 ,
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
+ + +
+ + +
+ + +
+ + +
Recuerda que…
En la Organización de
las Naciones Unidas se calcula
una cantidad llamada Índice
de Desarrollo Humano, HDI
(Human Development Index,
por sus siglas en inglés), que
mide el desarrollo humano de
un país o de una región. Para
ello, se utilizan tres categorías:
esperanza de vida, educación
y producto interno bruto. Este
índice se expresa con el número
HDI [0,1].
Tiempo
transcurrido
en horas
Número
de visitas
4 60
10 930
18 5 562
36 45 468
p Tabla 2
Interdisciplinariedad
Matemática y tecnolo-
gía industrial
Las funciones polinomiales
se aplican en la fabricación
de cajas para la envoltura de
productos. El diseño de dichas
cajas requiere la optimización
del material y de su capacidad.
Con esta función se calculan los consumos de electricidad en los próxi-
mos tres años:
p(2015) = 150 + 5(4 + 5(4 + 5(0,5 + 5(0,2 + 0,01 x 5))) = 213,75,
p(2016) = 150 + 6(4 + 6(4 + 6(0,5 + 6(0,2 + 0,01 x 6))) = 248,16,
p(2020) = 150 + 7(4 + 7(4 + 7(0,5 + 7(0,2 + 0,01 x 7))) = 295,11.
Shutterstock,
(2020).
524367469
p Persona cantando.
Dr. H Benalcázar, 2020](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-150-320.jpg)

![263
• ¿Cuáles serán los nuevos consumos eléctricos?
• ¿Cuántas escuelas y colegios deberán construirse y cuántos do-
centes deberán incorporarse sucesivamente?
• ¿Cuánta basura se producirá?
• ¿Cuántas rutas de transporte deberán generarse?
• ¿Cuántos policías deberán incorporarse para la seguridad ciudadana?
Estas son tan solo unas pocas interrogantes que deberíamos plantear-
nos. En este sentido, le dejamos al estudiante, como ejercicio, reflexio-
nar acerca de otros problemas en torno al crecimiento de la ciudad.
Igualmente, dejamos que el aprendiz investigue cómo obtener infor-
mación y cómo procesarla para responder cada una de las preguntas
planteadas. Además, deberá también averiguar sobre modelos mu-
cho más complejos que conduzcan a soluciones mucho más precisas.
Nota. Los modelos matemáticos de crecimiento urbano son mucho
más complejos que los que estamos proponiendo en esta sección.
Para precisar las ideas, suponemos que una ciudad ocupa una región
Ω(t) ⊂ R2
al instante t ≥ 0 de área A(t), que escribimos A(t) = a(Ω(t)).
Nos interesa la evolución de Ω(t) y, con esta, la de A(t), a la que pode-
mos modelar con una ecuación diferencial:
( )
( ) = ( ( )).
( )
= ( , ( ), 0,
( ) = .
2
0
0 0
t
A t a t
dA t
dt
función t A t atracciones, resistencias), t T
A T A
≥
donde el término atracciones se refiere a factores que motivan la mo-
vilización de las personas a esas nuevas zonas urbanas t
t t t
t T T
A t a t a t
( )
( ) = ( ) ( ),
, ]
( ) = ( ( )) ( ( )).
0
∪
∈
+
Ω(t) que se
ponen adherentes a Ω(t) como, por ejemplo, la calidad de servicios
(agua potable, electricidad, alcantarillado, vías de acceso, transportes,
escuelas, centros médicos, supermercados, etc.). El término resisten-
cias se refiere a las limitaciones de acceso debido a factores geográ-
ficos como quebradas, parques, carencia de vías de comunicación,
carencia de agua potable, etc. Todos estos elementos deben cuanti-
ficarse para construir la función (t, A(t), atracciones, resistencias) y la
nueva región Ω(t) = Ω(t)∪ Ω(t),
t
t t t
t T T
A t a t a t
( )
( ) = ( ) ( ),
, ]
( ) = ( ( )) ( ( )).
0
∪
∈
+
t
t t t
t T T
A t a t a t
( )
( ) = ( ) ( ),
, ]
( ) = ( ( )) ( ( )).
0
∪
∈
+
donde t [T0
, T]
tienen una área A(t) = a(Ω(t)) + a(Ω(t)).
t
t t t
t T T
A t a t a t
( )
( ) = ( ) ( ),
, ]
( ) = ( ( )) ( ( )).
0
∪
∈
+
t
t t t
t T T
A t a t a t
( )
( ) = ( ) ( ),
, ]
( ) = ( ( )) ( ( )).
0
∪
∈
+
Como se puede apreciar, las dificultades aparecen por doquier y este
es, aún, un modelo simplificado a regiones planas.
Son desafíos a superar por investigadores, científicos y por ustedes.
Eje transversal
Ciudadanía
Las soluciones en torno al creci-
miento de la ciudad conducen
a mejorar la calidad de vida de
la población. Esto es, la aplica-
ción de las funciones polino-
miales constituye una parte
de la estrategia para mejorar la
calidad de vida.
Shutterstock,
(2020).
102733505
Nos interesa la información cuantitativa que obtenemos de este mo-
delo simple con fines de planificación. Así, junto con este crecimiento
del área urbana, crecen las necesidades, algunas de las cuales se plan-
tean como interrogantes:
• ¿Cuánta agua potable se requerirá sucesivamente?
• ¿Cuántos kilómetros de alcantarillado deberán construirse?
p Niños en clases..
Interdisciplinariedad
Matemática
y economía
Los economistas utilizan de
manera frecuente las funciones,
sobre todo sus gráficas, para
visualizar el comportamiento,
por ejemplo, de la oferta y la
demanda, con el fin de deter-
minar los puntos de equilibrio
entre las dos variables.
Shutterstock,
(2020).
192800075
p Análisis gráfico de negocios..](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-152-320.jpg)

![265
a) En el sistema de coordenadas rectangu-
lares, representa gráficamente este con-
junto de datos.
b) Resuelveelsistemadeecuacionesymues-
tra que esta función está definida como:
( ) = 0,22 0,004 3 0,000 83 0,000 022 0,000 008 , 0.
2 3 4
+ + + + ≥
B t T T T T T
00 83 0,000 022 0,000 008 , 0.
2 3 4
+ + ≥
T T T T
c) Calcula B(12), B(18).
Diversidad funcional
en el aula
El hecho de que haya una discapacidad auditiva
no significa que el tono de voz con el que se ha-
bla debe ser exagerado o excesivo. Basta con que
haya claridad al momento de comunicarse.
Trabajo colaborativo
Trabajen en equipo y resuelvan.
Obtén un registro del número de au-
tos matriculados en los últimos 5 años.
Construye funciones polinomiales de
grados 2 con los primeros 3 datos y de
grado 3 con los primeros 4 datos. Los da-
tos del quinto año se utilizan para verifi-
car la tendencia o bondad de la función
construida, de modo que pueda servir
para pronosticar el crecimiento de autos
en los 5 años siguientes. Esta información
3
Busca en Internet datos de nuestro país
sobre el índice HDI. Recuerda que el HDI
es el Indice de Desarrollo Humano. Uti-
liza en forma apropiada la información
para construir un polinomio de grado
menor o igual que 4, que permita anali-
zar la evolución del HDI:
4
a) Calculen los valores de esta función para
las distancias dadas y verifiquen sus re-
sultados con las velocidades de la tabla.
b) Muestren que, a los 300 metros, la avio-
neta supera la velocidad requerida míni-
ma y despega.
c) Prueben que la función V es creciente en
el intervalo [0,300].
Una avioneta brinda servicios de trans-
porte de personas. Dispone de una pista
de 500 metros. Para despegar, requiere
que en los 300 metros se alcance una ve-
locidad mínima de 180 km/h. La veloci-
dad máxima que alcanza en el aire es de
360 km/h. En el despegue, en su máxima
potencia, se obtienen los siguientes datos:
5
Distancia recorrida (m) Velocidad alcanzada (m/s)
50 5,15
100 12,1
200 34,4
250 51,25
300 72,9
p Tabla 8
V x x x x x
( ) = 0,09 0,000 21 0,000 001 , si 0,300 ,
2 3
[ ]
+ + ∈
La función velocidad V, en términos de la
distancia recorrida x y con viento a favor,
se expresa como:
Dr. H Benalcázar, 2020
Para obtener los datos investiga en la página
web http://www.ecuadorencifras.gob.ec/docu-
mentos/web-inec/Estadisticas_Economicas/
Estadistica%20de%20Transporte/Publicacio-
nes/Anuario_de_Estad_de_Transporte_2013.
pdf
es útil con fines de planificación y regula-
ción del transporte.
Archivo editorial, 2020](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-154-320.jpg)




![270
Operaciones con sucesos.
Leyes de De Morgan
DCCD: M.5.3.9. Realizar operaciones con sucesos: unión, intersección, diferencia y complemento, leyes de Morgan, en la resolución de problemas.
Unión
Definición. Sean A, B subconjuntos de un conjunto E. Se denomina
unión de A y B al subconjunto de E, cuyos elementos pertenecen
al conjunto A o al conjunto B. A dicho conjunto lo notamos con
A ∪ B, es decir que
A ∪ B = {x ∈ E | x ∈ A ∨ x ∈ B}.
La función proposicional p(x) sobre E que interviene en el conjunto
A ∪ B está dada como p(x) : x ∈ E, tal que x ∈ A ∨ x ∈ B.
Además, para cada x ∈ E, la función proposicional p(x) se transforma
en una proposición, la cual es falsa (definición de disyunción) cuando
las proposiciones x ∈ A, x ∈ B son ambas falsas. En los casos restantes,
p(x) es siempre verdadera. Se tiene la siguiente equivalencia:
x ∈ A ∪ B ⇔ x ∈ A ∨ x ∈ B,
y la negación
x ∉ A ∪ B ⇔ x ∉ A ∧ x ∉ B.
La última proposición nos indica cuando un elemento x no pertenece
a la unión. Nótese que se ha utilizado una de las leyes de De Morgan:
¬ (p ∨ q) ⇔ [(¬p) ∧ (¬p)].
En la práctica, la unión de los conjuntos A y B, expresada en forma
tabular, se obtiene juntando en un solo conjunto los elementos de
A y de B. Los elementos que son comunes a los dos conjuntos se es-
criben una sola vez. Sean A, B, C tres subconjuntos de E. Se prueba que
A ∪ (B ∪ C) = (A ∪ B) ∪ C = (A ∪ C) ∪ B = C ∪ (B ∪ A).
Y este resultado común se escribe A ∪ B ∪C.
Intersección. Conjuntos disjuntos
Definición. Sean A, B subconjuntos de un conjunto E. Se denomina
intersección de A y B al subconjunto de E, cuyos elementos pertene-
cen a A y a B. A dicho conjunto lo notamos A∩B, es decir,
A ∩ B = {x ∈ E | x ∈ A ∧ x ∈ B}.
La función proposicional p(x) sobre E está definida como p(x): x ∈ E,
tal que x ∈ A ∧ x ∈ B. Para cada x ∈ E, la función proposicional
p(x) se transforma en una proposición que puede ser verdadera
o falsa. Es verdadera cuando x ∈ A y x ∈ B. Esto es, x ∈ A ∩ B. En los
casos restantes, p(x) es siempre falsa. Se tienen las siguientes equiva-
lencias:
x ∈ A ∩ B ⇔ x ∈ A ∧ x ∈ B,
x ∉ A ∩ B ⇔ x ∉ A ∨ x ∉ B.
La última equivalencia es la negación de la primera y nos muestra las
condiciones bajo las cuales un elemento x no pertenece a la intersec-
ción. Obsérvese que se ha utilizado una de las leyes de De Morgan:
¬ (p ∧ q) ⇔ [(¬p) ∨ (¬p)].
Recuerda que...
Sean A, B los subconjun-
tos de Z, definidos como sigue:
A = {7k + 3/k ∈ Z}.
B = {7m –18/m ∈ Z}.
A simple vista, estos conjuntos
no parecen ser iguales. La realidad
es diferente: estos dos conjuntos
son iguales.
Un elemento x del conjunto A
se escribe como x = 7k + 3;
mientras que un elemento y de
B se escribe como y = 7m –18,
donde k, m ∈ Z son escogidos
de manera apropiada.
De la igualdad de conjuntos pro-
baremos que: A ⊂ B y B ⊂ A.
Probemos que A ⊂ B, es decir,
todo elemento de A es un
elemento de B, que como
proposición se escribe:
∀ x, x ∈ A ⇒ x ∈ B.
En efecto, sea x ⊂ A existe k ∈ Z
tal que x = 7k + 3. Escribamos
x = 7k + 3 en forma apropiada,
de modo que x se escriba como
un elemento del conjunto B.
Tenemos x = 7k + 3 = 7k + 21 –
18 = 7 (k + 3) – 18 = 7m –18 ∈ B,
donde m = k + 3 ∈ Z. Así, x ∈ A
⇒ x ∈ B, o sea, A ⊂ B.
Probemos que B ⊂ A. Sea y ∈ B,
existe m ∈ Z, tal que y = 7m – 18.
Luego, y = 7m – 18 = 7m – 21 +3
y = 7(m – 3) + 3 ∈ B
Desequilibrio cognitivo
¿Qué relación existe entre
los conectivos lógicos: negación,
conjunción, disyunción?
Saberes previos
¿Cómo explicas qué es
un experimento aleatorio?](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-159-320.jpg)


![273
Trabajen en equipo, indaguen y resuelvan.
a) A = {2m | m ∈ E}, B = {3n | n ∈ E},
C = {6p | p ∈ E}.
a) Tomando en consideración que n (A ∩ T)
= 46 y n (A ∩ T ∩ B) = 32, entonces,
A ∩ T = [A ∩ TB] ∪ [A ∩ T∩ B],
n(BC
∩A∩T) = n(A∩T) – n(A∩T∩B)
= 46 – 32 = 14, que significa que de las 46
personas que usan autos particulares y
taxis, 14 no utilizan buses. Mediante un
razonamiento similar, muestren que de
55 personas que utilizan autos particulares
y buses, 23 no utilizan taxis y que de las 85
personas que utilizan buses y taxis, 53 no
utilizan autos particulares.
b) Puesto que n (A) = 120, n (A∩T)= 46,
n(A ∩ B)= 55 y del hecho que los conjuntos
A ∩ B (A ∩ B ∩ T), A ∩ T (A ∩ B ∩ T),
A∩ B∩ T,A∩ (B∪ T)C
sondisjuntos,talque
A = [A ∩ B (A ∩ B ∩ T)] ∪ [A ∩ T (A ∩
B ∩ T)] ∪ [A ∩ B ∩ T] ∪ [A ∩ (B ∩ T]C
Sugerencia: mediante diagramas de
Venn–Euler, identifiquen estos conjuntos.
Tenemos
n([A∩B(A∩B∩T)])=n(A∩B)–n(A∩B∩T)
= 55 – 32 = 23,
n([A∩T(A∩B∩T)])=n(A∩T)–n(A∩B∩T)
= 46 – 32 = 14.
Se sigue que n(A ∩ (B ∪ T)C
)
= n(A)–n([A∩ B(A ∩B ∩T)]) – n([A ∩
T(A ∩ B ∩T)]) – n([A ∩ B ∩T).
Continúa el proceso.
En cada ítem se definen tres subcon-
juntos A, B, C del conjunto referencial
E = {j ∈ ⎥ |j| ≤ 500}. Indica en pala-
bras qué representa cada conjunto dado.
Demuestra que A ∩ B = C y determina
el número de elementos de A, B y C.
4
b) A = {5m | m ∈ E}, B = {3n | n ∈ E},
C = {15p | p ∈ E}.
a) A={2m| m∈ E},B={3n| n∈ E},C={5p| p∈ E}.
En cada ítem se definen tres subcon-
juntos A, B, C del conjunto referencial
E = {j ∈ Z ⎮ |j| ≤ 51}. Determina los si-
guientesconjuntos:(A∩B)C,(BA)∩ C,
C (A ∩ B), (C A) B, al igual que el nú-
mero de elementos de cada uno de ellos.
5
b) A={2m| m∈E},B={6n|n∈ E},C={4p|p∈E}.
c) A = {4m | m ∈ E}, B = {8n | n ∈ E},
C = {8p | p ∈ E}.
El Departamento de Transportes del can-
tón XYZ es el encargado de la planifica-
ción de su red de transportes. Entre uno
de los estudios que realiza, está la identi-
ficación del tipo de transporte utilizado:
autos particulares, taxis y buses, entre las
regiones R1
y R2
de la ciudad. Para ello,
se recoge una muestra de las personas
en el lugar de destino y se designa con A
al conjunto de personas que usa autos
particulares, con T al conjunto de usua-
rios de taxis, con B al conjunto de usua-
rios de buses y con E al conjunto referen-
cial. Se obtienen los siguientes resultados:
6
Tipo de
transporte
A T B A y T A y B B y T
A y T
y B
Número
de usuarios
120 65 210 46 55 85 32
Diversidad funcional
en el aula
La discapacidad no debe asustarnos. Muy
por el contrario, la discapacidad puede ser una
herramienta positiva, pues puede enseñarnos
a valorar la diversidad humana.
Trabajo colaborativo
p Tabla 9
Archivo editorial, (2020).
Dr. H Benalcázar, 2020](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-162-320.jpg)










![Evaluación sumativa
284
M.5.3.9. Realizar operaciones con sucesos: unión,
intersección, diferencia y complemento, leyes de
Morgan, en la resolución de problemas.
xxxxxx
En cada ítem se definen tres subcon-
juntos A, B, C del conjunto referencial
E = {j ∈ ⎮ |j| ≤ 500}. En palabras, indi-
ca qué representa cada conjunto dado.
Demuestra que A ∩ B = C y determina
el número de elementos de A, B y C.
M.5.1.40. Aplicar las operaciones entre polino-
mios de grados ≤ 4, esquema de Hörner, teorema
del residuo y sus respectivas propiedades para
factorizar polinomios de grados ≤ 4 y reescribir
los polinomios.
4
Heteroevaluación
a) d(x) = 4x3
– 8, ∀x ∈ .
C(x) = 3x + 9, ∀x ∈ .
r(x) = 2x – 12, ∀x ∈ .
¿Cuál es el polinomio D(x)?
a) A = {3 m | m ∈ E}, B = {7 n | n ∈ E},
C = {21 p | p ∈ E}.
b) A = {2 m | m ∈ E}, B = {11 n | n ∈ E},
C = {22 p | p ∈ E}.
b) D(x) = x4
– 3x2
+ 2x – 1,
d(x) = x2
+ 1,
C(x) = x2
– 4.
¿Cuál es el polinomio del residuo r(x)?
Completa el término que se pide en
cada división, en donde el polinomio
D(x) es el dividendo, d(x) es el divisor,
C(x) es el cociente y r(x) es el residuo.
2
a) P(x) + Q(x).
b) P(x) + R(x).
c) Q(x) · R(x).
d) P(x) · Q(x).
e) P(x) : R(x).
f) Q(x) : R(x).
g) El resto de la división de P(x) por x – 1.
h) P(–1).
i) P(–2) + [Q(–2)]².
Determina el resto sin necesidad de
hacer la división:
3
M.5.3.10. Calcular el factorial de un número na-
tural y el coeficiente binomial para determinar
el binomio de Newton.
Calcula.
5
a) 2! + 4! + 6! + 8!
a) + −
1
2
.
3
2
.
5 5
a a
. b)
+ −
1
2
.
3
2
.
5 5
a a .
Aplica el proceso de la división y deter-
mina el cociente c de dividir p(x) para
q(x).
7
Sea a R. Escribe el desarrollo del bi-
nomio de Newton.
6
a) x + 1.
b) x – 1.
c) x – 2.
d) x + 3.
e) 2x + 1.
a) x – 2.
b) x + 3.
c) 2x – 1.
d) 2x + 1.
e) x + 7.
Dados los polinomios:
P(x) = 4x² – x + 2; x ∈ .
Q(x) = x³ + x – 1; x ∈ .
R(x) = 2x – 1, x ∈ .
Halla:
1
b) + + +
1
2!
1
3!
1
4!
1
5!
.
i. p x x x q x x
p x x x q x x
( ) =2 6, x , ( ) =2 1, x .
( ) =3 7 5, x , ( ) =3 1, x .
2
2
− + ∀ ∈ + ∀ ∈
− − ∀ ∈ − ∀ ∈
ii.
p x x x q x x
p x x x q x x
( )=2 6, x , ( )=2 1, x .
( )=3 7 5, x , ( )=3 1, x .
2
2
− + ∀ ∈ + ∀ ∈
− − ∀ ∈ − ∀ ∈
a)
(x3
– 3x2
+ 2)
(x + 3)
.
b)
(x4
– 6x3
+ 3x2
– 1)
(x + 2)
(3x3
– x + 5)
(x – 2)
c)](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-173-320.jpg)

![286
Respuestas a las evaluaciones sumativas
Unidad 1 (páginas 78 - 79)
1. a) S = 2(x2 + 1), S =
12
5
.
b)
S = –x2 + 7x – 5, S = –242.
4. a)
A B=
1
3
,0 .
A B= 10,9
] ].
A B=
1
3
,0 .
A B= 10,9
] ].
b)
6. a) x =
1
2
, y =
–1
2
b)
x = 0, y = 2 3.
7. a) El sistema de ecuaciones no
tiene solución.
b) a =
–1 041
9
, b =
–57
90
.
8. Media aritmética = 67,06
Mediana = 67,5
Moda = 68,3
9. b
10. b
11. d
12. a) Respuesta A = 2
b) Respuesta C = 1
c) Respuesta C = 2
4. a) F(–1) = –5, F(1) = 5,
pendiente m = 5, F(x) es
creciente.
b) F(–1) = 3, F(1) = 1, pendiente
m = –1, F(x) es decreciente.
c) F(–1) =
–3
4
, F(2) =
–9
2
,
pendiente m =
–5
4
, F(x) es
decreciente.
5. a) fog
( ) x
( )
= f g x
( )
( )= f
x 3
2
=2
x 3
2
+3= x, x .
C(x)=
C0x, si 0 x 50,
C0x 0,01x, si 50 x 100,
C0x 0,15x si x 100.
C(x)=
2x, si 0 x 50,
2x 0,01x, si 50 x 100,
2x 0,15x si x 100.
fog
( ) x
( )
= f g x
( )
( )= f
x 3
2
=2
x 3
2
+3= x, x .
C(x)=
C0x, si 0 x 50,
C0x 0,01x, si 50 x 100,
C0x 0,15x si x 100.
C(x)=
2x, si 0 x 50,
2x 0,01x, si 50 x 100,
2x 0,15x si x 100.
6.
a)
fog
( ) x
( )
= f g x
( )
( )= f
x 3
2
=2
x 3
2
+3= x, x .
C(x)=
C0x, si 0 x 50,
C0x 0,01x, si 50 x 100,
C0x 0,15x si x 100.
C(x)=
2x, si 0 x 50,
2x 0,01x, si 50 x 100,
2x 0,15x si x 100.
b)
fog
( ) x
( )
= f g x
( )
( )= f
x 3
2
=2
x 3
2
+3= x, x .
C(x)=
C0x, si 0 x 50,
C0x 0,01x, si 50 x 100,
C0x 0,15x si x 100.
C(x)=
2x, si 0 x 50,
2x 0,01x, si 50 x 100,
2x 0,15x si x 100.
( )
( )
( ) ( )
( ) ( )
+ ⋅ = ⋅ + ⋅ =
− ⋅ = ⋅ − ⋅ =
−
+ ⋅ − = ⋅ − ⋅ =−
+ ⋅ − = ⋅ − ⋅ + − ⋅ =
u v w u w v w
u w v u v v w
u w u w u u w w
v w u u v v u v v w u w
15
2
.
10,5
2
.
22,75.
2 3 2 3 2 6 . 4 67,5.
( )
( )
( ) ( )
( ) ( )
+ ⋅ = ⋅ + ⋅ =
− ⋅ = ⋅ − ⋅ =
−
+ ⋅ − = ⋅ − ⋅ =−
+ ⋅ − = ⋅ − ⋅ + − ⋅ =
u v w u w v w
u w v u v v w
u w u w u u w w
v w u u v v u v v w u w
15
2
.
10,5
2
.
22,75.
2 3 2 3 2 6 . 4 67,5.
( )
( )
( ) ( )
( ) ( )
+ ⋅ = ⋅ + ⋅ =
− ⋅ = ⋅ − ⋅ =
−
+ ⋅ − = ⋅ − ⋅ =−
+ ⋅ − = ⋅ − ⋅ + − ⋅ =
u v w u w v w
u w v u v v w
u w u w u u w w
v w u u v v u v v w u w
15
2
.
10,5
2
.
22,75.
2 3 2 3 2 6 . 4 67,5.
( )
( )
( ) ( )
( ) ( )
+ ⋅ = ⋅ + ⋅ =
− ⋅ = ⋅ − ⋅ =
−
+ ⋅ − = ⋅ − ⋅ =−
+ ⋅ − = ⋅ − ⋅ + − ⋅ =
u v w u w v w
u w v u v v w
u w u w u u w w
v w u u v v u v v w u w
15
2
.
10,5
2
.
22,75.
2 3 2 3 2 6 . 4 67,5.
( )
( )
( ) ( )
( ) ( )
+ ⋅ = ⋅ + ⋅ =
− ⋅ = ⋅ − ⋅ =
−
+ ⋅ − = ⋅ − ⋅ =−
+ ⋅ − = ⋅ − ⋅ + − ⋅ =
u v w u w v w
u w v u v v w
u w u w u u w w
v w u u v v u v v w u w
15
2
.
10,5
2
.
22,75.
2 3 2 3 2 6 . 4 67,5.
2. a)
b)
c)
d)
3. a) − = + −
u v u v
( ).
7. a
8. a
9. d
C(48) = $96.
C(51) = $101,49.
C(100) = $199.
C(150) = $277,5.
C(200) = $370.
Unidad 3 (páginas 174 - 175)
1. a) Falso.
b) Verdadero.
c) Falso.
d) Falso.
2. a) a = 25 000; b = 1 375; c = 62,5.
b) P(t)=25000+1375(t–1950)
+ 62,5(t – 1 950)2
.
Para t ≥ 1 950, t – 1 950 ≥ 0,
si 1 950 ≤ t1
t2
, resulta
0 ≤ t1
– 1 950 ≤ t2
– 1 950,
0 ≤ (t1 – 1 950)2
≤ (t2
– 1 950)2,
de donde P(t1) P(t2).
c) P(2007) = 306 437,5;
P(2020) = 427 500.
5. a) ( )
( )
( )
=
= −
= −
u
u
u
40,63 .
46,38 .
17,11 .
b)
c)
6. Perímetro: +
4 2 29.
7. b)
4
3
,
4
3
,
3
4
, 3
4
,
8. a)
−1
2
,
3
4
9. c) ,
1
2
,
1
2
,
3
4
,
3
4
10. d) x = 20.
11. d) x = 10.
Unidad 2 (páginas 118 - 119)
1. a)
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
ángulo de
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
+
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
con la hori-
zontal 90° + α con:
b)
β
α α α α
( )
( )
( ) ( )
− =
−
− = −
=
−
= = ⋅ ∀ ∈ ≠
u v u w
v w
sen
u v u v
. .
15
2
2 ,
41 20 2 ,
5 2
2 41 20 2
.
. 0 , con 0.
Ángulo que forma
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
–
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
con la horizontal 90° – β con:
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
α
( )
( )
+ = +
=
+
+ = = =
v w
sen
u v w u v u w
41 20 2 ,
5 2
2 41 20 2
,
. ( )
15
2
2 , . 0, .
15
2
2.
β
α α α α
( )
( )
( ) ( )
− =
−
− = −
=
−
= = ⋅ ∀ ∈ ≠
u v u w
v w
sen
u v u v
. .
15
2
2 ,
41 20 2 ,
5 2
2 41 20 2
.
. 0 , con 0.
Unidad 4 (páginas 214 - 215)
1. a) Ecuación vectorial:
u t t
x t
y t t
y
( ) (0, 1), t .
( ) 0
( ) 1, t .
.
= − ∈
=
= − ∈
∀ ∈
Ecuaciones paramétricas:
u t t
x t
y t t
y
( ) (0, 1), t .
( ) 0
( ) 1, t .
.
= − ∈
=
= − ∈
∀ ∈
Ecuación cartesiana:
x = 0,
u t t
x t
y t t
y
( ) (0, 1), t .
( ) 0
( ) 1, t .
.
= − ∈
=
= − ∈
∀ ∈
b) Ecuación vectorial:
u t t t
x t t
y t t
x y x y
( ) ( 3 2, 1), t .
( ) 3 2
( ) 1, t .
( , ) tal que 3 1 0.
2
= − − + ∈
=− −
= + ∈
∈ + − =
Ecuaciones paramétricas:
u t t t
x t t
y t t
x y x y
( ) ( 3 2, 1), t .
( ) 3 2
( ) 1, t .
( , ) tal que 3 1 0.
2
= − − + ∈
=− −
= + ∈
∈ + − =
Ecuación cartesiana:
u t t t
x t t
y t t
x y x y
( ) ( 3 2, 1), t
( ) 3 2
( ) 1, t .
( , ) tal que 3 1
2
= − − + ∈
=− −
= + ∈
∈ + −
u t t t
x t t
y t t
x y x y
( ) ( 3 2, 1), t .
( ) 3 2
( ) 1, t .
( , ) tal que 3 1 0.
2
= − − + ∈
=− −
= + ∈
∈ + − =
c)
Ecuación vectorial:
u t t t
x t t
y t
( )
1
3
2, 2 1 , t .
( ) 2
1
3
,
( ) 1 2 t, t .
= + − ∈
= +
=− + ∈
α α α α
( ) ( )
= = ⋅ ∀ ∈ ≠
u v u v
. 0 , con 0.
α α α
( )
= = ⋅ ∀ ∈ ≠
v u v
. 0 , con 0.
c)
β
α α α α
( )
( )
( ) ( )
− =
−
− = −
=
−
= = ⋅ ∀ ∈ ≠
u v u w
v w
sen
u v u v
. .
15
2
2,
41 20 2 ,
5 2
2 41 20 2
.
. 0 , con 0.
β
α α α
( )
)
( )
− =
−
= −
=
−
= = ⋅ ∀ ∈ ≠
u w
w
v u v
.
15
2
2,
41 20 2 ,
5 2
2 41 20 2
.
. 0 , con 0.
d) t = 2020,236 82 ó t = 2020
mes de marzo.
3. Por definición
⋅ = + = + = ⋅
A B a a b b a a b b B A
1 2 1 2 2 1 2 1
4. a)
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2.
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2.
b)
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2.
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2.
c)
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2
λ λ
λ λ
λ λ
( ) ( )
( ) ( )
( )
+ = − = +
− = − = −
+ = − + + =
u v w u v
u v w u v
u xv u xv w
2 1, 3 ; 2 ; para = 4.
2 3 5, 1 ; 2 3 ; para =
1
5
.
3 3 x,3 x ; 3 = 2.
](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-175-320.jpg)
 = 12t – 56t2
+ 32t3, tR.
(4PQ)(t) = 12t – 56t2 + 32t3, tR.
9. b) 5 cm.
10. a) 10 u2.
11. b) grado (P) = 3.
12. a) –P(t)=–1–2t+3t2.
4. Opuestos aditivos –P, –Q dados
como:
(–P)(t)= –2 + 4t + 9t2
, t∈R,
(–Q)(t)= 1 – 2t2
+ t4
, t∈R,
a) (P + Q)(t) = 1 + 4t – 7t2
+ t, t∈R.
b)(P–Q)(t)=3–4t–11t2
+t4
, t∈R.
c)(Q–P)(t)=–3+4t+11t2
–t4
, t∈R.
3. a)
Recta que pasa por (1/3,0) y es
paralela al vector (0, 1).
Recta que pasa por (0, 1/a) y es
paralela al vector (1, –3).
x
L y y
x y
a
L
a
x x
1
3
, y .
1
3
,0 (0,1)
3
1
.
0,
1
(1, 3)
= ∀ ∈
= + ∈
+ =
= + − ∈
b)
x
L y y
x y
a
L
a
x x
1
3
, y .
1
3
,0 (0,1)
3
1
.
0,
1
(1, 3)
= ∀ ∈
= + ∈
+ =
= + − ∈
5. a) grado (P) = 2
b) Si P(t) = a + bt + ct2,
entonces a = 0, b = 5, c = –8.
c) P(t) = t(5 – 8t),
P(3,5) = 3,5(5 – 8(3,5)) = –80,5.
6. (2P–3Q)(t)=20–8t–5t2, tR.
(2P – 3Q)(1) = 7.
7. a) ( ) ( )
( ) ( )
+ −
= ≠
+ −
= + + ≠
P a h P a
h
h
P a h P a
h
a h h
–5; 0.
–3 4 ; 0.
b)
( ) ( )
( ) ( )
+ −
= ≠
+ −
= + + ≠
P a h P a
h
h
P a h P a
h
a h h
–5; 0.
–3 4 ; 0.
8. a)
(P2 – Q2)(t) = 9 – 12t + 3t2 + 8t3 – 16t4,
tR.
(P + Q)(P – Q)(t) = 9 – 12t + 3t2 + 8t3 –
16t4, tR.
e) P(x)–R(x)=4x2–3x–1, tR.
f) Q(x)–R(x)=x3–x, tR.
g) Resto de la división: 5.
+
= + + ≠
x x
x
x
x
x
–4 2
–1
4 3
5
–1
, 1.
2
h) P(–1) = 7
i) P(–2) + [Q(–2)]2 = 141.
2. a) D(x)=12x4+36x3–22x–84,
tR.
b)
r(x)=x+3, tR.
3. a) –52.
b) 75.
c) 27.
4. a) A conjunto de múltiplo de 3
de elementos de E.
B conjunto de múltiplo de 7 de
elementos de E.
C conjunto de múltiplo de 21 de
elementos de E.
Ten presente x∈A ∩ B, x∈A o sea
x = 3m con m∈E, x∈B con x = 7n,
n∈E. Luego 3m = 7n. Esta igualdad
es verdadera si m es múltiplo
de 7 y n múltiplo de 3, así x es
múltiplo de 21.
b) A conjunto de números
pares de elementos de E.
B conjunto de números múlti-
plos de 11 de elementos de E.
C conjunto de números múlti-
plos de 22 de elementos de E.
De la igualdad 2m = 11n con
m, n∈E, se sigue que m múltiplo
de 11 y n par, o sea 11n es múlti-
plo de 22.
5. a) 41 066; 2! + 4! + 6! + 8! = 2(1 +
12(1 + 30(1 + 56))).
b)
1
2!
+
1
3!
+
1
4!
+
1
5!
=
1
2
1+
1
3
1+
1
4
1+
1
5
=
43
60
.
7. i) b) x – 1
ii) a) x – 2
8) d) 5.
9) a)
6!
3!(6 – 3)!
10) c)
a+
1
2
5
= a5
+
5
2
a4
+
5
2
a3
+
5
4
a2
+
5
16
a+
1
32
.
a+
3
2
5
= a5
+
15
2
a4
+
45
2
a3
–
135
4
a2
+
405
16
a–
243
32
.
a+
1
2
5
=a5
+
5
2
a4
+
5
2
a3
+
5
4
a2
+
5
16
a+
1
32
.
a+
3
2
5
=a5
+
15
2
a4
+
45
2
a3
–
135
4
a2
+
405
16
a–
243
32
.
6. a)
b)
4. a)
b)
h h h
h h h
0 ...
0 ...
3 2 1
3 2 1
h h h
h h h
0 ...
0 ...
3 2 1
3 2 1
X0
– h1
X0
– h2
X0
– h3
X0
X0
+ h3
X0
+ h2
X0
+ h1
X0
X0
– h1
X0
– h2
X0
– h3
X0
X0
+ h3
X0
+ h2
X0
+ h1
X0](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-176-320.jpg)
![Bibliografía
288
Benalcázar, H. (2008). Curso elemental de Geometría. Quito: PDF publi-
cado por el autor en la Facultad de Ingeniería, Universidad Central
del Ecuador.
------------------- (2012a). Matemática para Bachillerato. Tomo 2 y
tomo 3. Quito: Preprinter (por publicarse).
Castro, L. (2013). Matemática. Quito: Archivo editorial C. Ltda.
Galindo, E. (2015). Estadística, métodos y aplicaciones. Quito: Procien-
cia Editores.
Gómez, R., Wills, D., Guarin, H. y Londoño, N. (1976). Matemática
moderna estructurada (Vols. 1-6). Bogotá: Editorial Norma.
Lara, J. y Benalcázar, H. (1991). Fundamentos de análisis matemático
(Vols. I-III). Quito: Editorial Centro de Matemática, Universidad
Central del Ecuador.
Leithold, L. (1994). El cálculo (7.a
ed.). México D. F.: Grupo Mexicano
Mapasa, S. A. de C. V.
Negro, A., Pérez, S., Cacho, S. y Thio de Pol, S. (1977). Cerca de la Mate-
mática (3). Madrid: Editorial Alhambra.
Pérez, J., Caro, V. y Obonaga, E. (1986). Matemática (Vols. 1-6). Bogotá:
Editorial Pime Editores S. A.
Sáenz, R., Lara, J., Benalcázar, H. y León, H. (2003). Matemática bási-
ca (2.a
ed.). Quito: Editorial Centro de Matemática, Universidad
Central del Ecuador.
Zemansky, M. (1967). Introducción al álgebra y análisis moderno.
Barcelona: Editorial Montaner y Simón, S. A.
Webgrafía
Funciones como modelos matemáticos (s. f.), [en línea]. Departamento
de Matemática de la Universidad de Sonora. Disponible en: http://
www.mat.uson.mx/~jldiaz/Documents/Funcion/4-funciones-mode-
los-jl.pdf [2016, 8 de junio].
Matemática. Función cuadrática, parábolas y ecuaciones de segundo
grado (2014), [en línea]. Gobierno de la Ciudad de Buenos Aires. Mi-
nisterio de Educación. Disponible en: http://www.buenosaires.gob.ar/
areas/educacion/curricula/pdf/matematica_cuadratica_13_06_14.
pdf [2016, 7 de abril].
Probabilidad (s. f.), [en línea]. Instituto Nacional de Tecnologías Edu-
cativas y de Formación del Profesorado. Disponible en: http://sauce.
pntic.mec.es/~jpeo0002/Archivos/PDF/T02.pdf [2016, 7 de junio].](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-177-320.jpg)

![Adrián Paenza
Uno puede hacerse pasar por adivino o por una persona muy
entrenada en predecir el futuro o aventurar lo que va a pasar en
la Bolsa de Valores: basta con aprovechar la rapidez con la que
crecen las potencias de un número.
Este es un ejemplo muy interesante. Supongamos que tenemos
una base de datos de 128 000 personas. (Por las dudas, no crean
que sean tantas, ya que la mayoría de las grandes empresas las
tienen, las compran o las averiguan). De todas formas, para lo que
quiero invitarles a pensar, podríamos empezar con un número
más chico, e igualmente el efecto sería el mismo.
Supongamos que uno elige alguna acción o algún commodity
cuyo precio cotice en la Bolsa. Digamos, para fijar las ideas, que
uno elige el precio del oro. Supongamos también que ustedes se
sientan frente a su computadora un domingo por la tarde. Buscan
la base de datos que tienen y seleccionan las direcciones electr
nicas de todas las personas que allí figuran. Entonces, a la mitad
de ellas (64 000) les envían un mail diciéndoles que el precio del
oro va a subir al día siguiente (lunes). Y a la otra mitad les envían
un mail diciéndoles lo contrario: que el precio del oro va a bajar.
(Por razones que quedarán más claras a medida que avance con
el ejemplo, excluiremos los casos en los que el oro permanece con
el precio constante en la apertura y el cierre.)
Cuando llega el lunes, al finalizar el día, el precio del oro o bien
subió o bien bajó. Si subió, hay 64 000 personas que habrán re-
cbido un mail de ustedes diciéndoles que subiría. Claro, qué im-
potancia tendría. Haber acertado un día lo que pasaría con el oro
iene poca relevancia. Pero sigamos con la idea.
El lunes a la noche, de las 64 000 personas que habían recibido
su primer mail diciéndoles que el precio del oro subiría, ustedes
seleccionan la mitad (32 000) y les dicen que el martes volverá
a subir. Y a la otra mitad, los otros 32 000, les envían un mail
diciéndoles que va a bajar.
Cómo conseguir un contrato como consultor [...]
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/1ro-bachillerato-matematica-f2-210918005049/85/1ro-bachillerato-matematica-f2-179-320.jpg)














