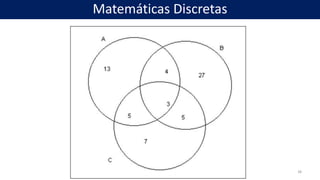
El documento aborda conceptos fundamentales de matemáticas discretas, centrándose en la definición y operaciones relacionadas con conjuntos, tales como la intersección, unión, diferencia y complementos. También incluye ejemplos de conjuntos, así como ejercicios prácticos para resolver problemas aplicando estos conceptos. Se resalta la importancia de las matemáticas discretas en la computación y su relevancia en la solución de problemas en este ámbito.