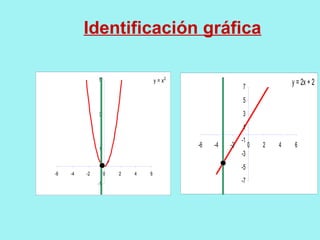
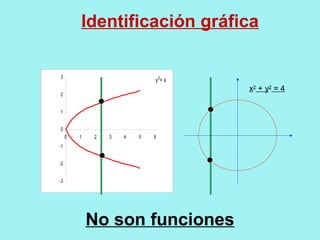
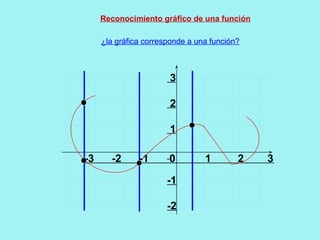
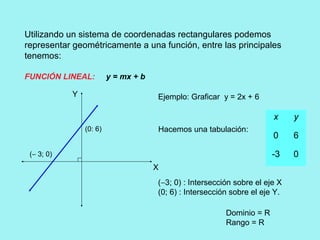
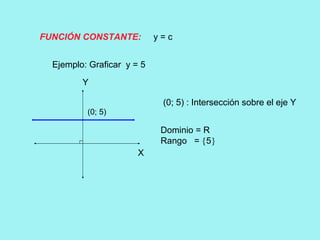
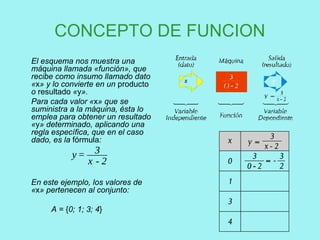
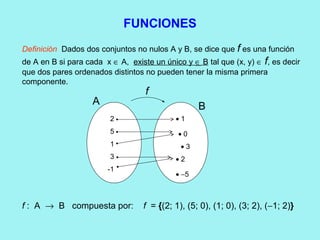
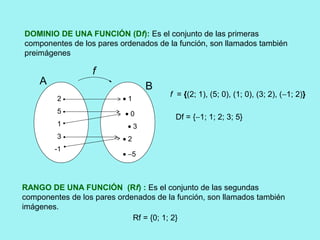
El documento presenta conceptos básicos de conjuntos y funciones matemáticas. Introduce las nociones de pertenencia, conjunto vacío y subconjunto. Explica el producto cartesiano de dos conjuntos y provee ejemplos. Luego, define relación y función, y distingue entre ambos conceptos. Finalmente, describe cómo representar funciones gráficamente usando coordenadas cartesianas, incluyendo ejemplos de funciones lineales y constantes.

2. 1. Nociones de Conjuntos
a) Definiciones
Conjunto: Es una colección de objetos bien definidos,
considerados como una sola unidad.
Pertenencia (Є) : Si un objeto “p” es elemento de un
conjunto C, entonces p pertenece a C y su notación es: p Є C.
Si p no pertenece a C, se denota: p Є C
Conjunto vacío (Ø): Es aquel conjunto que no posee
elementos. También se denota como: { }
Subconjunto ( ): Un conjunto A es “subconjunto” de otro
conjunto B si todos los elementos que pertenecen a A, son
también elementos de B.

3. b)Producto Cartesiano
Dados los conjuntos A y B , su producto cartesiano ( A × B )
está formado por cada uno de los pares ordenados donde el
primer elemento pertenece a A y el segundo a B :
A x B = { (a,b) / a Є A y b Є B }
Ejemplo:
Si A = { a, b, c } y B = { 1, 2 } , entonces:
A x B = { (a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}

4. a b c
1
2 .
.
.
.
.
.
A
B
Gráficamente:

5. Relaciones y Funciones
• El concepto de Relación-Función es uno
de los más importantes en Matemáticas.
Comprenderlo y aplicarlo se verá
retribuido muchas veces.

6. Correspondencia
• La noción de correspondencia
desempeña un papel fundamental en el
concepto de Relación – Función.
• En nuestra vida cotidiana frecuentemente
hemos tenido experiencia con
correspondencias o RELACIONES.

7. Ejemplos de Correspondencias o
RELACIONES
• En un almacén, a cada artículo le corresponde
un precio.
• A cada nombre del directorio telefónico le
corresponde uno o varios números.
• A cada número le corresponde una segunda
potencia.
• A cada estudiante le corresponde un promedio
de calificaciones

8. Ejemplos de Correspondencia
(Relaciones – Funciones)

9. Definición de Relación y de
Función
 Relación es la correspondencia de un primer
conjunto, llamado Dominio, con un segundo
conjunto, llamado Rango, de manera que a
cada elemento del Dominio le corresponde uno
o más elemento del Recorrido o Rango.
 Una Función es una relación a la que se
añade la restricción de que a cada valor del
Dominio le corresponde uno y sólo un valor
del recorrido.
 (Todas las funciones son relaciones, pero no
todas las relaciones son funciones)

10. Toda ecuación es una Relación,
pero no toda ecuación es una
Función
 Esta afirmación la podemos ilustrar
mediante la siguiente animación
¿Por qué se produjo el error?

11. Haga clic en las ecuaciones que están ubicadas
en el recuadro de la derecha, las que Ud.
considere que son funciones.
¿Por qué
algunas de las
ecuaciones
son
Funciones?

12. Todas las Relaciones pueden ser
graficadas en el Plano Cartesiano

13. CONCEPTO DE FUNCION
El esquema nos muestra una
máquina llamada «función», que
recibe como insumo llamado dato
«x» y lo convierte en un producto
o resultado «y».
Para cada valor «x» que se
suministra a la máquina, ésta lo
emplea para obtener un resultado
«y» determinado, aplicando una
regla específica, que en el caso
dado, es la fórmula:
En este ejemplo, los valores de
«x» pertenecen al conjunto:
A = {0; 1; 3; 4}
3y =
x - 2

14. OBSERVACIONES
• La máquina, llamada función, no puede procesar
cualquier valor que se le asigne a la variable
independiente. Por ejemplo: x = 2.
• Llamamos dominio al conjunto formado por todos los
valores que puede asumir la variable independiente “x”.
Df = {0; 1; 3; 4}
• Llamamos rango al conjunto formado por todos los
valores que puede asumir la variable dependiente “y”.
Rf = {-3/2; 3/2; 3}
• Los pares ordenados formados por las variables
independiente y dependiente son elementos que le
pertenecen a un conjunto llamado función:
f = {(0;-3/2), (1; 3), (3;3), (4; 3/2)}

15. FUNCIONES
Definición Dados dos conjuntos no nulos A y B, se dice que f es una función
de A en B si para cada x ∈ A, existe un único y ∈ B tal que (x, y) ∈ f, es decir
que dos pares ordenados distintos no pueden tener la misma primera
componente.
A B
f
2
1
5
-1
3
• 1
• 0
• 2
• −5
• 3
f : A → B compuesta por: f = {(2; 1), (5; 0), (1; 0), (3; 2), (−1; 2)}

16. DOMINIO DE UNA FUNCIÓN (Df): Es el conjunto de las primeras
componentes de los pares ordenados de la función, son llamados también
preimágenes
RANGO DE UNA FUNCIÓN (Rf) : Es el conjunto de las segundas
componentes de los pares ordenados de la función, son llamados también
imágenes.
A B
f
2
1
5
-1
3
• 1
• 0
• 2
• −5
• 3
Df = {−1; 1; 2; 3; 5}
Rf = {0; 1; 2}
f = {(2; 1), (5; 0), (1; 0), (3; 2), (−1; 2)}

17. Gráfica de unaGráfica de una
funciónfunción
Cuando la regla que define la
función f está dada por una
ecuación en x, la gráfica de f es
el conjunto de puntos (x,y) en el
plano que satisfacen dicha
ecuación.
Gráficamente una función se reconoce cuando toda
recta vertical corta a la gráfica de la función en a
lo más un punto.

18. EjemploEjemplo f(x) = x + 3 en [-1;2]
-1 0 1 2
5
4
3
2
1

19. Identificación gráfica
y = x2
-1
1
3
5
-6 -4 -2 0 2 4 6
y = 2x + 2
-7
-5
-3
-1
1
3
5
7
-6 -4 -2 0 2 4 6

20. y2
= x
-3
-2
-1
0
1
2
3
0 1 2 3 4 5 6
Identificación gráfica
No son funciones
x2
+ y2
= 4

21. Reconocimiento gráfico de una función
-3 -2 -1 0 1 2 3
3
2
1
-1
-2
¿la gráfica corresponde a una función?

22. GRÁFICAS EN COORDENADAS RECTANGULARES
Un punto se ubica en el plano por medio de sus coordenadas
rectangulares, escritas en la forma de un par ordenado.
“a” : Abscisa de “P”
“b” : Ordenada de “P”
(a; b) : Coordenadas de “P”
Y (Eje de ordenadas)
X (Eje de abscisas)
P=(a; b)
a
b

23. Utilizando un sistema de coordenadas rectangulares podemos
representar geométricamente a una función, entre las principales
tenemos:
FUNCIÓN LINEAL: y = mx + b
Ejemplo: Graficar y = 2x + 6
(−3; 0) : Intersección sobre el eje X
(0; 6) : Intersección sobre el eje Y.
X
Y
(− 3; 0)
(0: 6) Hacemos una tabulación:
x y
0 6
-3 0
Dominio = R
Rango = R

24. FUNCIÓN CONSTANTE: y = c
Ejemplo: Graficar y = 5
(0; 5) : Intersección sobre el eje Y
Y
X
(0; 5)
Dominio = R
Rango = {5}