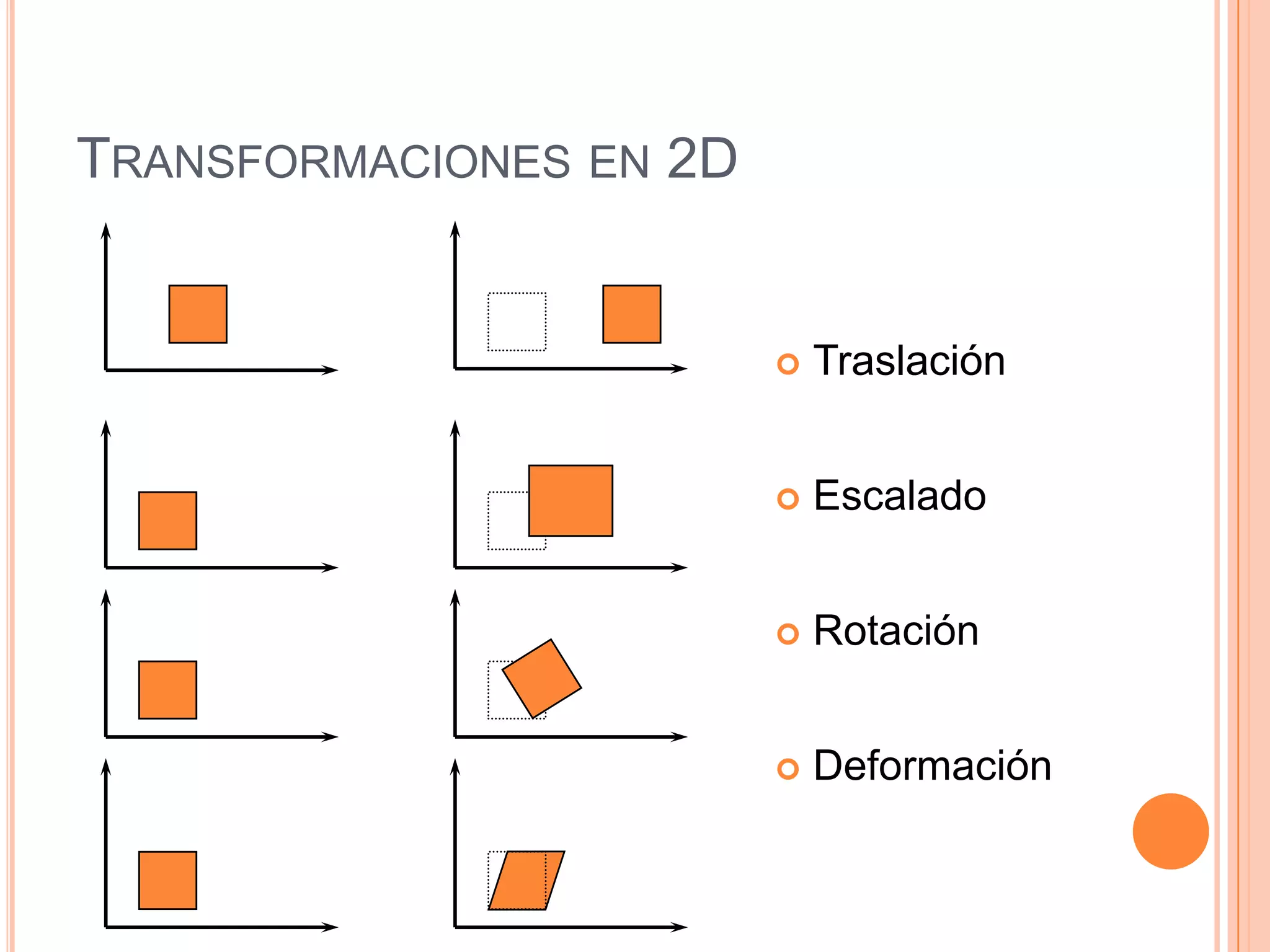
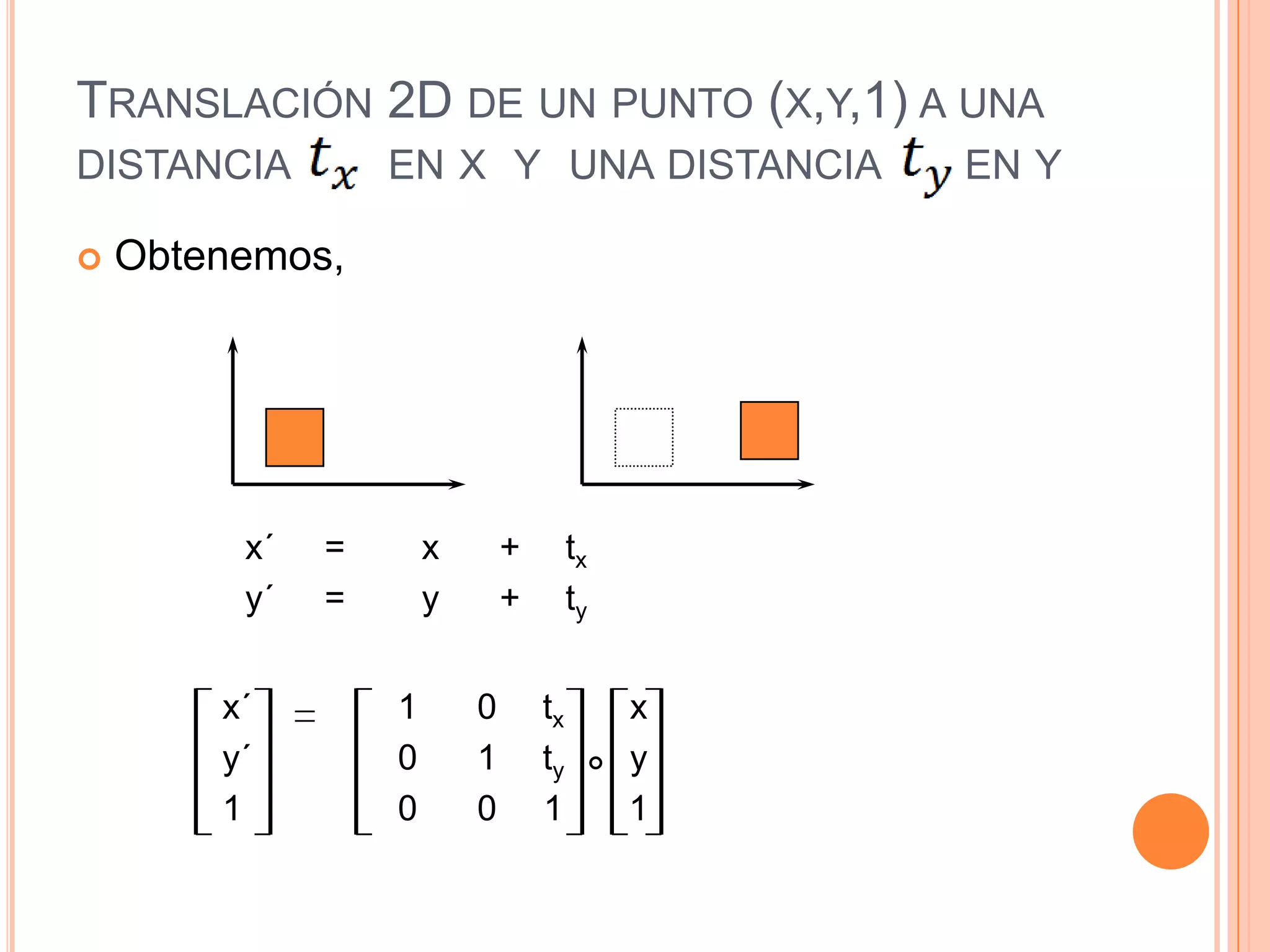
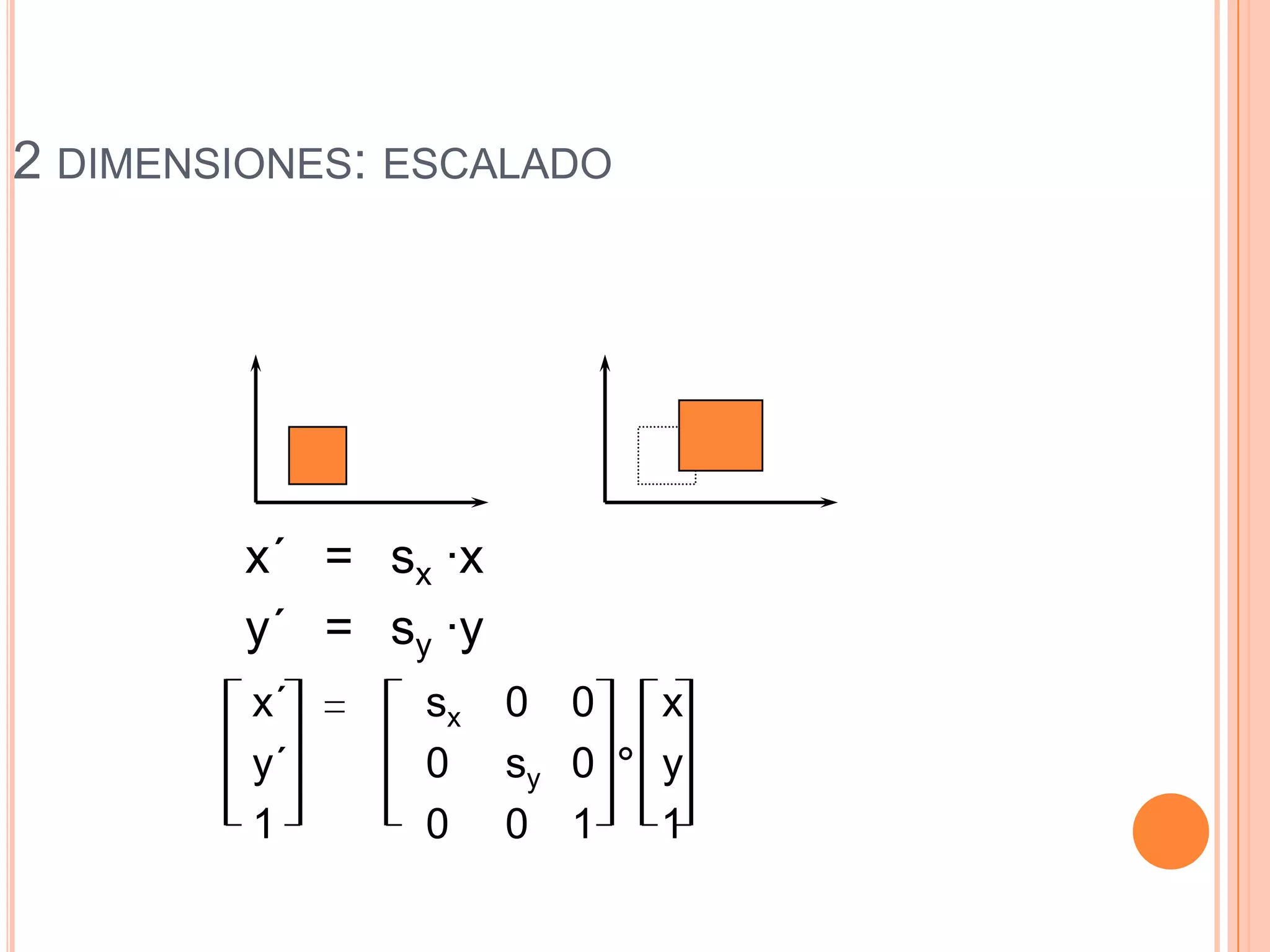
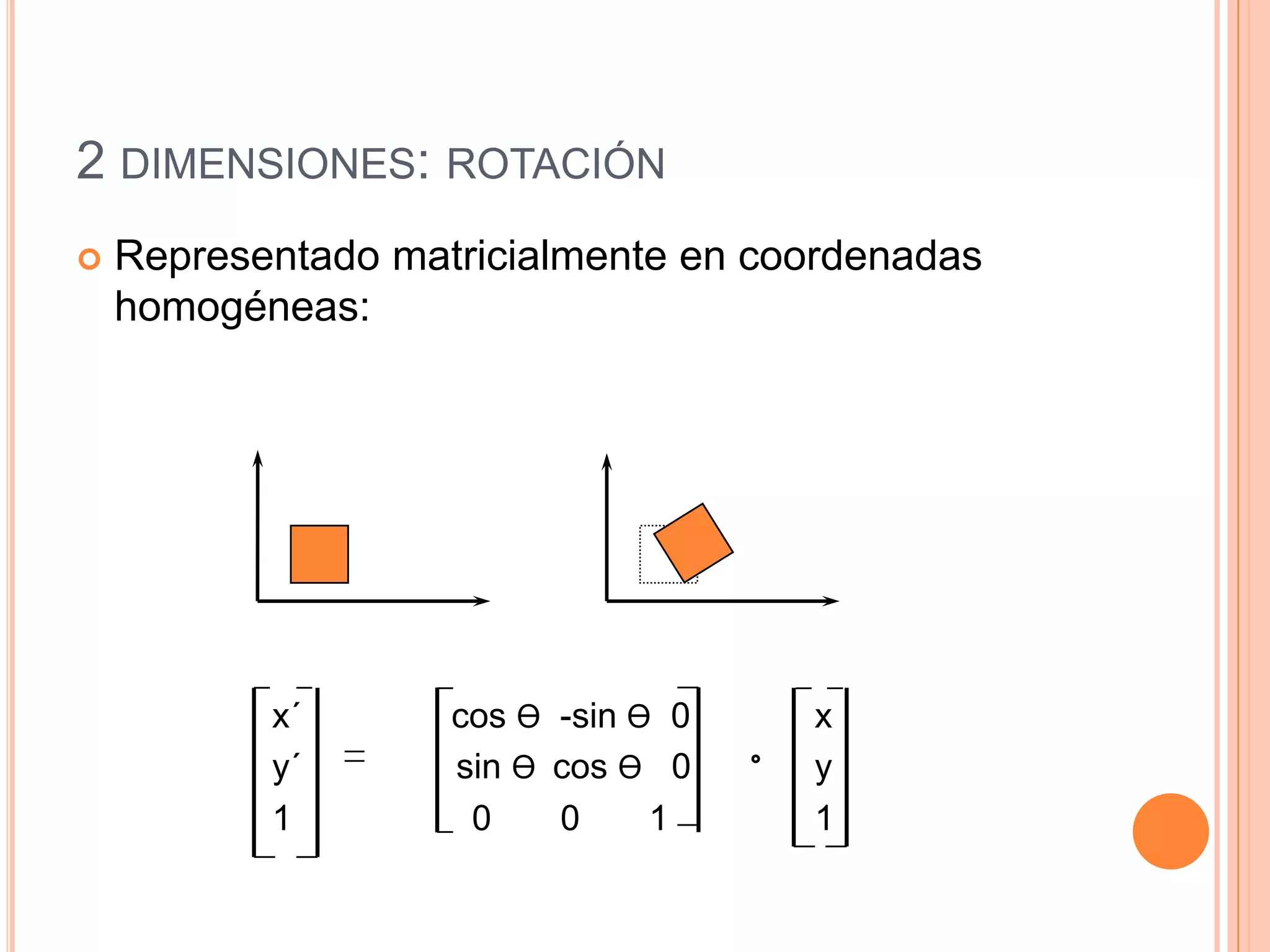
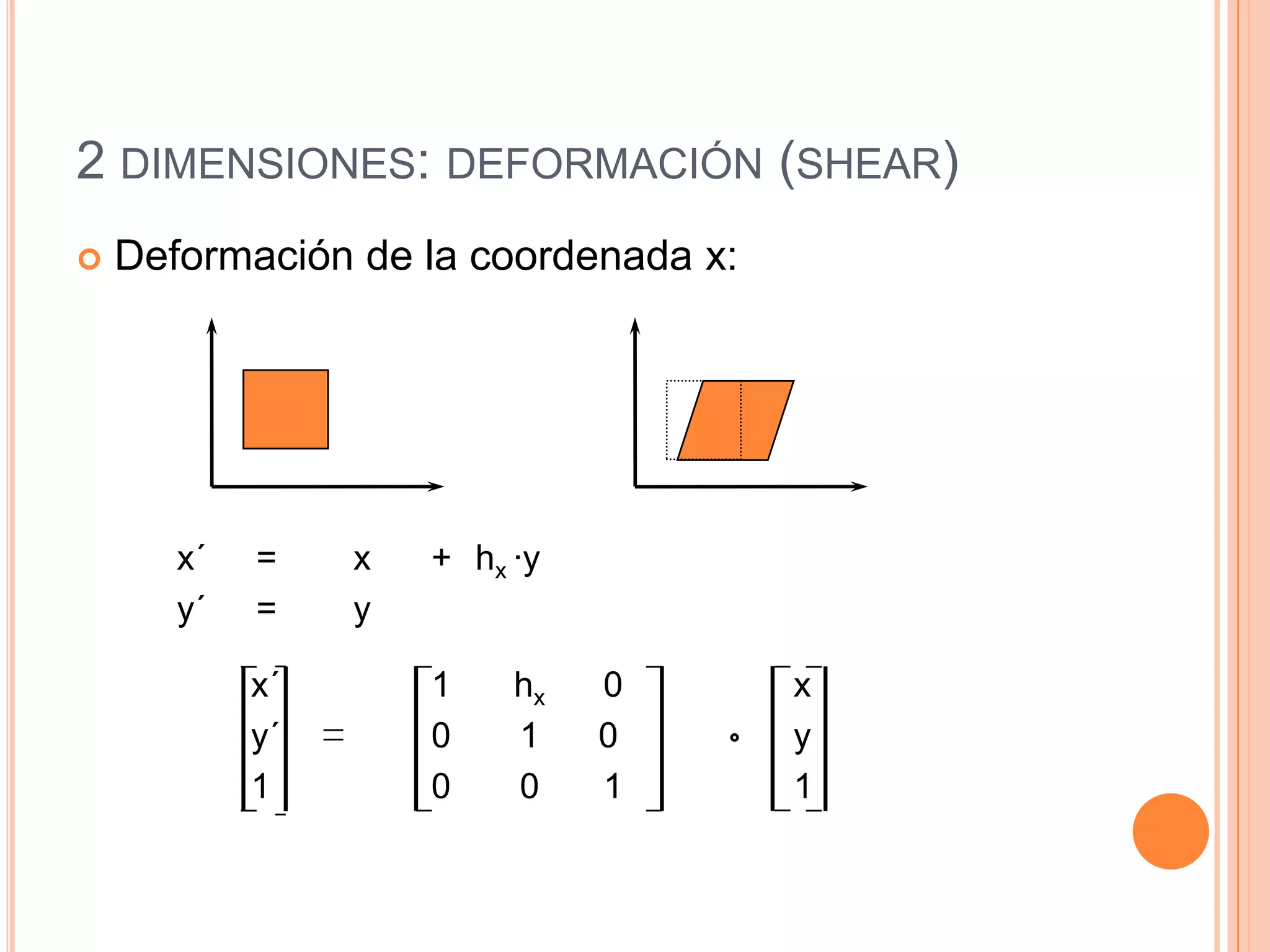
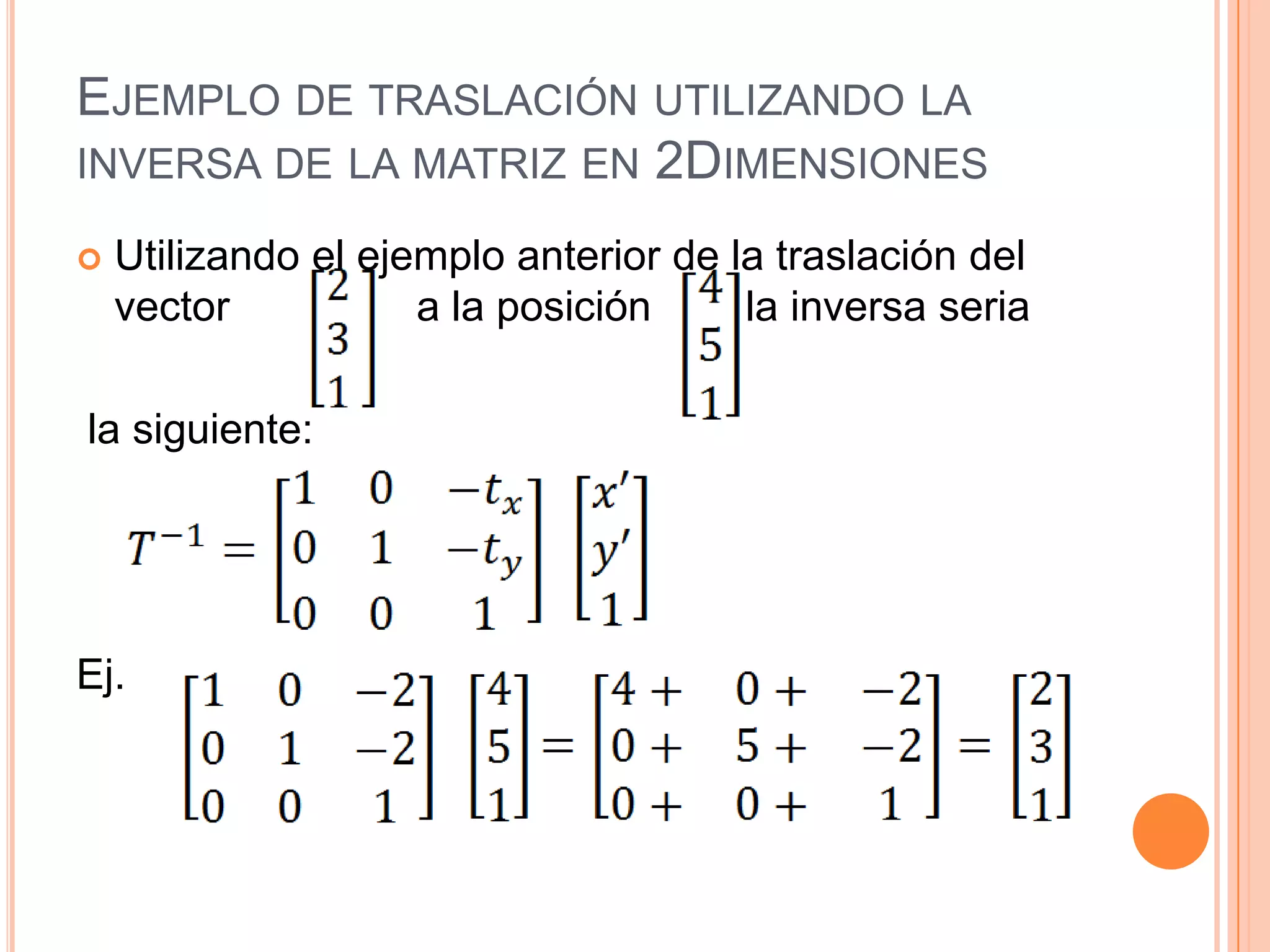
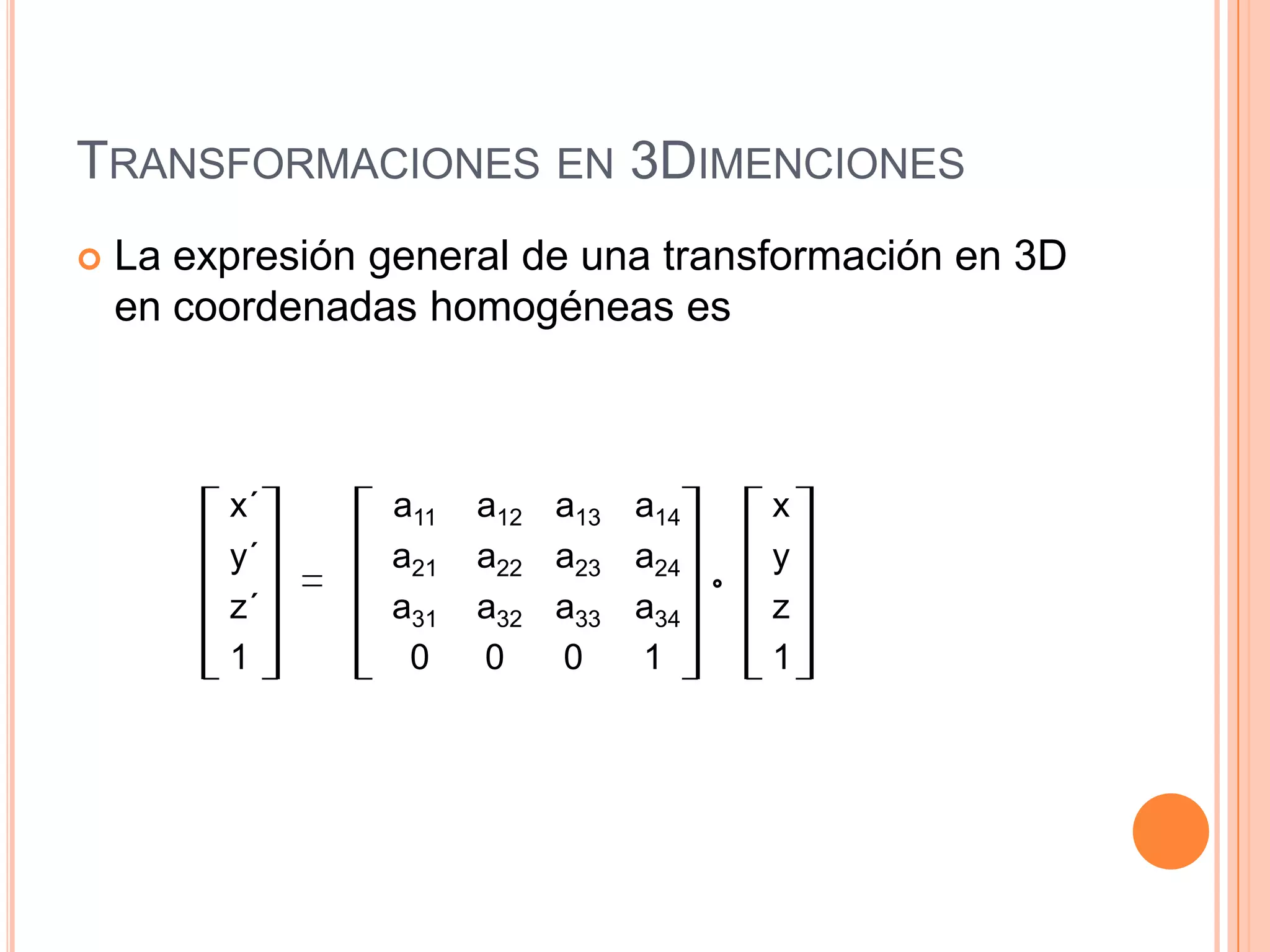
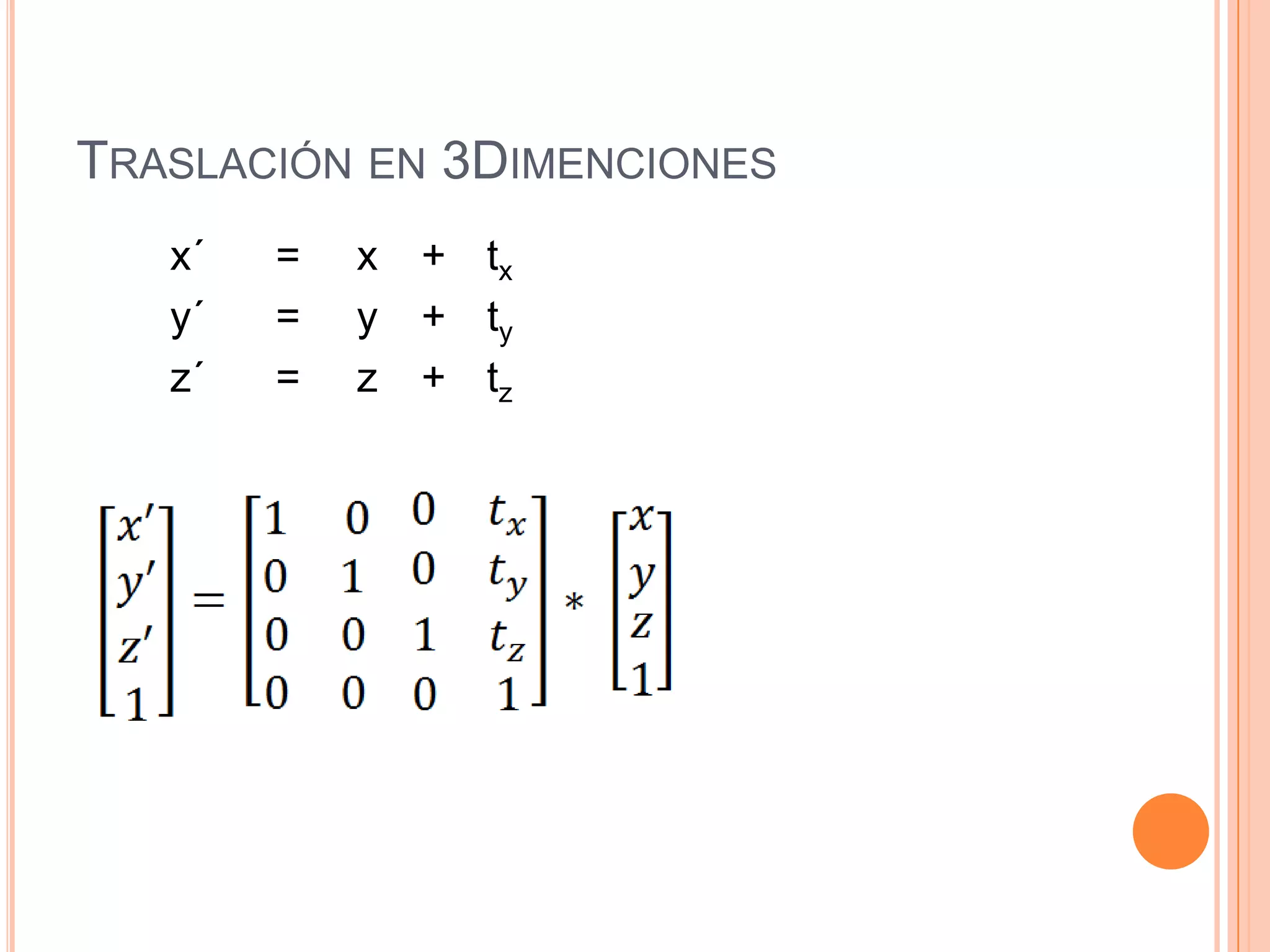
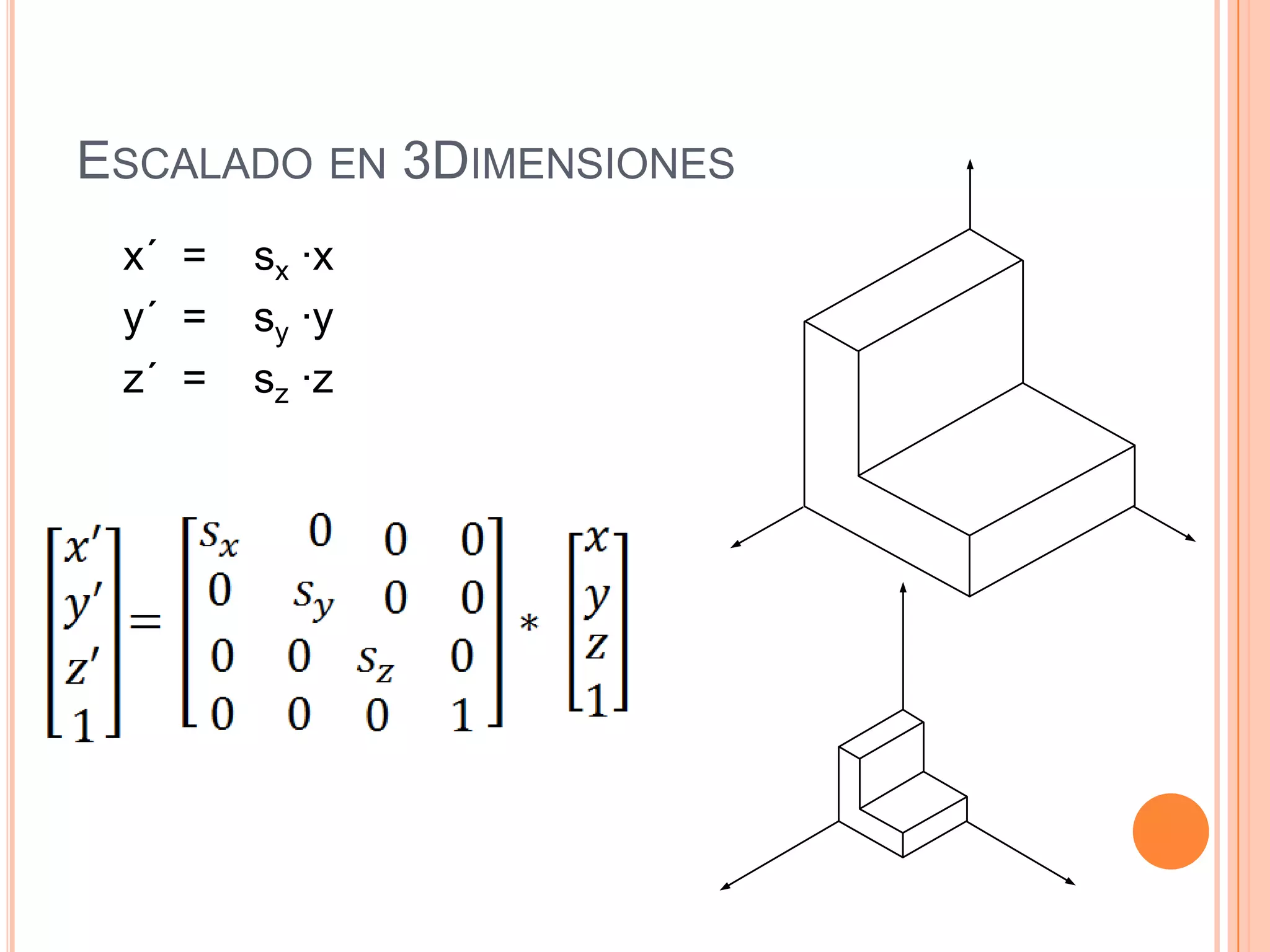
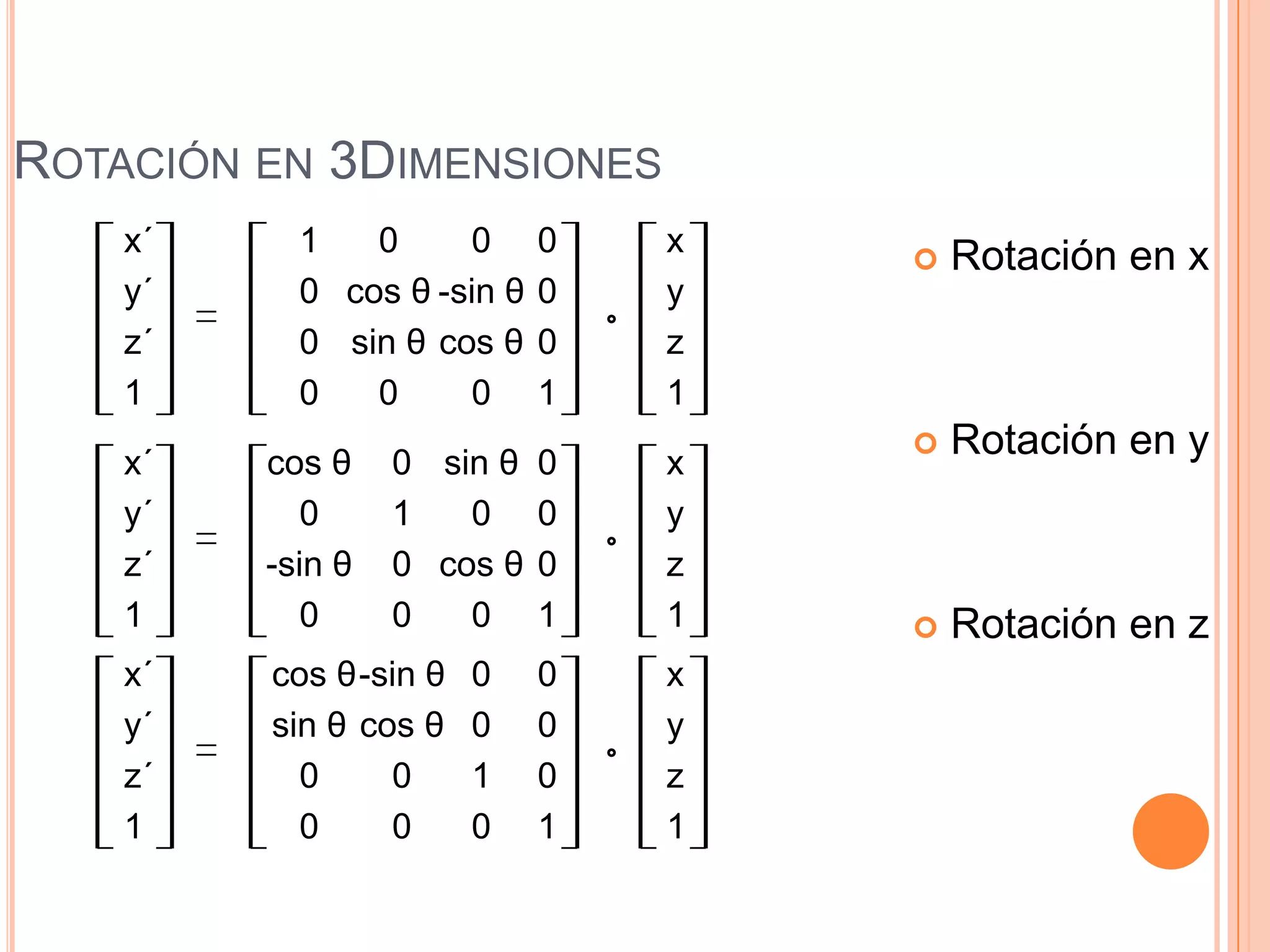
Este documento resume la historia y definición de las matrices, incluyendo diferentes tipos como matrices cuadradas, nulas e identidad. Explica cómo se pueden usar matrices para representar transformaciones como traslación, escalado y rotación en 2D y 3D, y cómo la composición de transformaciones se puede lograr mediante el producto de matrices. Finalmente, discute cómo las matrices se implementan eficientemente en computadoras para gráficos 3D.

1. CAPITULO 6MATRICESSra. Ruth CuebasSr. Jose Moreno

2. HistoriaLas matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley introduce la notación matricial como una forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.

3. La utilización de matrices (arrays) constituye actualmente una parte esencial de los lenguajes de programación, ya que la mayoría de los datos se introducen en los ordenadores como tablas organizadas en filas y columnas , hojas de cálculo y bases de datos.

4. DefinicionUna matriz es una tabla cuadrada o rectangular de datos (llamados elementos o entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz

5. y una columna es cada una de las líneas verticales.A una matriz con m filas y n columnas se le denomina matriz m-por-n (escrito m×n), y a m y n dimensiones de la matriz.

6. Las dimensiones de una matriz siempre se dan con el número de filas primero y el número de columnas después. Comúnmente se dice que una matriz m-por-n tiene un orden de m × n ("orden" tiene el significado de tamaño)

7. Dos matrices se dice que son iguales si son del mismo orden y tienen los mismos elementos.

8. Al elemento de una matriz que se encuentra en la fila i-ésima y la columna j-ésima se le llama elemento i,j o elemento (i,j)-iésimo de la matriz. Se vuelve a poner primero las filas y después las columnas

9. La matriz es una matriz 4x3. El elemento A[2,3] o a2,3 es 7.

10. La matriz es una matriz 1×9, o un vector fila con 9 elementos

11. ALGUNOS TIPOS DE MATRICES Dada una matriz A, se llama traspuesta de Aa la matriz que se obtiene cambiando ordenadamente las filas por las columnas.

12. Matriz CuadradaAquella matriz que tiene igual número de filas que de columnas, m = n, se dice que la matriz es de orden n

13. IDENTIDADEs una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales a 1. También se denomina matriz unidad.

14. Matriz NulaSi todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n

15. La matriz opuesta de una dada es la que resulta de sustituir cada elemento por su opuesto. La opuesta de A es -A.

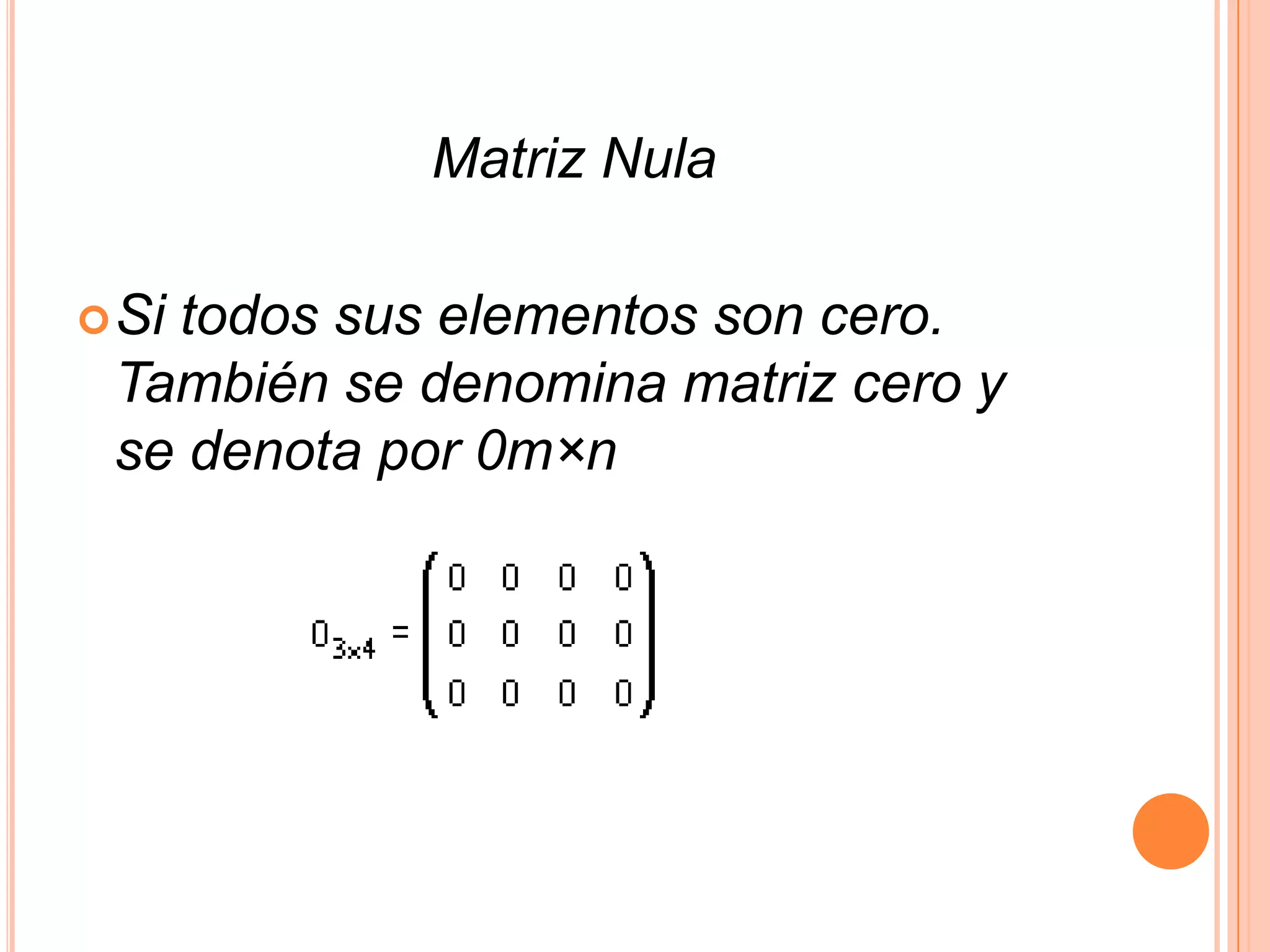
16. Suma o adición Dadas las matrices m-por-n ,A y B, su sumaA + B es la matriz m-por-n calculada sumando los elementos correspondientes (A + B)[i, j] = A[i, j] + B[i, j]

17. Porejemplo:Sumar cada uno de los elementos homólogos de las matrices a sumar.

18. PropiedadesAsociativaDadaslas matrices m×nA, B y C A + (B + C) = (A + B) + C ConmutativaDadaslas matrices m×nA y B A + B = B + A

19. Propiedades (cont.)Existencia de matriz cero o matriznula A + 0 = 0 + A = A Existencia de matrizopuesta A + (-A) = 0

20. Producto de matricesEl producto de dos matrices se puede definir sólo si el número de columnas de la matriz izquierda es el mismo que el número de filas de la matriz derecha. Si A es una matriz m×n y B es una matriz n×p, entonces su producto matricialAB es la matriz m×p (m filas, p columnas).

21. Porejemplo:

22. Matrices, Transformaciones y Coordenadas Homogéneas: 3DimensionesPara conseguir las transformaciones básicas ( translación, rotación, escalado, deformación, en general las transformaciones afines) se utilizan matrices de transformación.Realizando algunos cambios a las matrices, se pueden combinar para conseguir una matriz resultante que sirva para varias transformaciones.

23. Coordenadas HomogéneasLas coordenadas homogéneas son un instrumento usado para describir un punto en el espacio proyectivo. Se usan como un sistema alternativo de coordenadas para trabajar en el espacio pues este puede verse como un subconjunto del espacio.

24. Sistema de Coordenadas HomogéneasUn objeto se representa por polígonos.Un polígono es una colección de vértices y aristas.Para transformar un objeto se transforman sus vértices.Si todos los puntos se expresan en coordenadas homogéneas, todas las transformaciones se pueden expresar como multiplicación.En coordenadas homogéneas a cada punto P(x,y) se le añade una tercera coordenada, W de forma que se representa mediante una tripleta, P(x,y,W).

25. Sistema de Coordenadas HomogéneasSi la coordenada W es distinta de cero, se puede normalizar la tripleta, dividiéndola por W, (x/W,y/W,1), seguirá representando al mismo punto. (x/W) y (y/W) se llaman coordenadas cartesianas del punto homogéneo.Cada punto expresado en coordenadas homogéneas representa una línea en el espacio 3D.Cuando se normaliza el punto, se obtiene un punto de la forma (x,y,1). La normalización de un punto equivale a proyectar sobre el plano W = 1. Los puntos en el infinito no se proyectan sobre este plano.

26. Explicaremos primero las transformaciones en 2Dimenciones y luego las de 3DimencionesExiste un numero de representaciones homogéneas equivalentes para cada coordenada (x,y) seleccionando un valor no cero para w.Por conveniencia escogeremos w=1, para cada posición bidimensional con las coordenadas homogéneas (x,y,1)

27. Transformaciones en 2DTraslaciónEscaladoRotaciónDeformación

28. Translación 2D de un punto (x,y,1) a una distancia en x y una distancia en yObtenemos,x´ 1 0 tx xy´ 0 1 ty y 1 0 0 1 1x´ = x + txy´ = y + ty

29. x´ sx 0 0 xy´ 0 sy 0 y 1 0 0 1 12 dimensiones: escaladox´ = sx ·xy´ = sy ·y

30. 2 dimensiones: rotaciónx´ cos Ѳ -sin Ѳ0 xy´ sin Ѳ cos Ѳ0 y1 0 01 1Representado matricialmente en coordenadas homogéneas:

31. 2 dimensiones: deformación (shear)Deformación de la coordenada x:x´ 1 hx 0 xy´ 0 10 y1 0 0 1 1x´ = x + hx ·yy´ = y

32. Ejemplo de traslación en 2DSi queremos trasladar a dos unidades un vector en el plano obtenemos;

33. Inversa de la matriz transformadaEn realidad la inversa de la matriz es fácil de encontrar y el efecto que produce es “ undo” o sea regresar a la matriz original.2D

34. Ejemplo de traslación utilizando la inversa de la matriz en 2DimensionesUtilizando el ejemplo anterior de la traslación del vector a la posición la inversa seria la siguiente:Ej.

35. Transformaciones en 3DimencionesLa expresión general de una transformación en 3D en coordenadas homogéneas esx´ a11 a12 a13 a14 xy´ a21 a22 a23 a24 yz´ a31 a32 a33 a34 z1 0 0 0 1 1

36. Matriz de transformación M44Describe todas las transformaciones: traslación, escalado, rotación, deformación, etc...La composición de transformaciones se realiza mediante el producto de matrices.El producto de dos matrices es una herramienta que permite conectar dos transformaciones. Aplicar dos transformaciones sucesivas a un punto es equivalente a aplicar a ese punto el producto de las matrices de las respectivas transformaciones.

37. Traslación en 3Dimenciones x´ = x + tx y´ = y + ty z´ = z + tz

38. Escalado en 3Dimensiones x´ = sx ·x y´ = sy ·y z´ = sz ·z

39. x´ 1 0 0 0 xy´ 0 cos θ -sin θ 0 yz´ 0 sin θ cos θ 0 z1 0 0 0 1 1x´ cos θ 0 sin θ 0 xy´ 0 1 0 0 yz´ -sin θ 0 cos θ 0 z1 0 0 0 1 1x´ cos θ -sin θ 0 0 xy´ sin θ cos θ 0 0 yz´ 0 0 1 0 z1 0 0 0 1 1Rotación en 3DimensionesRotación en xRotación en yRotación en z

40. Deformación en 3Dimenciones10 00 1 0 0 0 1 0 0 0 0 1 100 0 1 0 0 k 1 0 0 0 0 1 10 0 1 1 0 k0 1 0 0 0 0 1

41. Inversa de la matriz en 3Dimensiones

42. Composición de transformacionesSe puede aplicar sucesivas transformaciones a un puntoAl resultado de la primera transformación Se aplica una segunda transformaciónLa composición de trans. Se realiza mediante el producto de matrices

43. Ejemplo de composiciónSupongamos una nueva escala para un objeto por un factor 2 en x al punto(1,1,1) del origenS(2,1,1) ; T(-1,-1,-1); S*T =

44. Implementación a la computadoraEn una concatenación de dos matrices de 3D en orden de(4x4) serian 64 multiplicaciones usando el método estándar de mult. De matrices.Es mas eficiente utilizar un una matriz de una dimensión de 12 elementos y sustituirla por la matriz general de transformaciones 3D;Obtenemos, =a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33a34 0 0 0 1 a0a1a2a3 a4 a5 a6 a7a8a9a10a11 0 0 0 1

45. ConclusiónEste capitulo nos enseña como atreves de las matemáticas (transformación de matrices) podemos aplicarlo para el uso de gráficos en el uso de la computadora. Así que el usuario de sistemas de gráfica realizadas en computadoras puede seguir con gran felicidad inconsciente del empleo de matrices dentro de las rutinas que permiten sus creaciones.