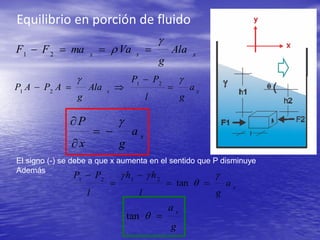
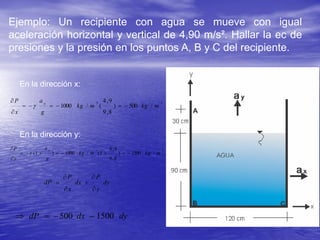
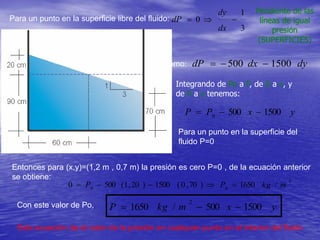
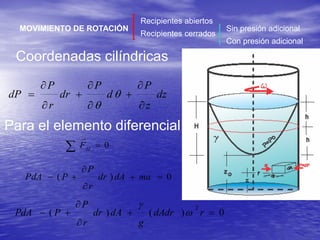
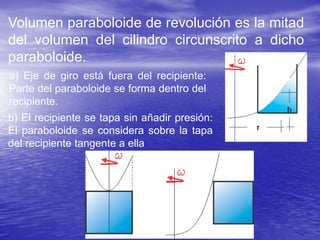
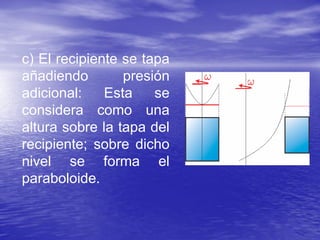
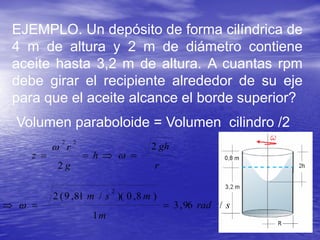
Este documento describe los conceptos de traslación y rotación de masas líquidas. Explica que cuando un fluido se mueve horizontalmente con aceleración constante, su superficie libre adopta la forma de un plano inclinado cuya pendiente depende de la aceleración. También analiza cómo varía la presión dentro de un fluido sometido a movimiento vertical u rotatorio, derivando ecuaciones para describir estas variaciones. Finalmente, presenta ejemplos numéricos ilustrativos.

1. MECANICA
DE LOS
FLUIDOS
Ing. Alejandro Mayori
5 TRASLACION Y ROTACION
DE MASAS LIQUIDAS

2. - Estudio Fluidos sometidos a movimientos de
traslación o rotación con aceleración constante
- Fluidos están en equilibrio relativo
- Las partículas de los fluidos no se mueven
- Fluidos están libres de tensiones cortantes
5 TRASLACION Y ROTACION
DE MASAS LIQUIDAS
5.1 Introducción

3. - La superficie libre del fluido adopta forma
plano inclinada
- La pendiente plano se determina por :
5.2 Movimiento Horizontal
tan q =
a (aceleracion lineal de recipiente)
g (aceleracion de la gravedad)

4. Equilibrio en porción de fluido
xxx
Ala
g
VamaFF

  21
ax
xx
a
gl
PP
Ala
g
APAP



 21
21
x
a
gx
P 



El signo (-) se debe a que x aumenta en el sentido que P disminuye
Además
x
a
gl
hh
l
PP 
q





tan2121
g
a x
qtan

5. - La superficie libre del fluido adopta forma
plano plano
- Presión incrementa o disminuye
5.3 Movimiento vertical
p = ℎ (1
+
−
a(aceleracion del recipiente)
g (aceleracion de la gravedad)

6. La ecuación básica de la
estática de fluidos expresa
que:
Para un movimiento con una
aceleración az
)1()(
g
a
ag
z
P z
z




g
z
P
 



7. dz
g
a
dPdz
g
a
dP
P z
zz
)1()1(
0 0
   
dz aumenta en el sentido que dP disminuye,
entonces:
z
g
a
P z
)1(  
EJEMPLO:
Hallar la presión en un líquido contenida en un recipiente que se mueve
verticalmente :
a) Cuando sube con una aceleración de 4,9 m/s².
b) Cuando baja con una aceleración de 4,9 m/s².
c) Cuando el depósito cae.
d) Cuando el depósito sube con una aceleración igual a la gravedad.
e) Cuando el depósito sube con una retardación igual a la gravedad.
+
-

8. Ejemplo: Un recipiente con agua se mueve con igual
aceleración horizontal y vertical de 4,90 m/s². Hallar la ec de
presiones y la presión en los puntos A, B y C del recipiente.
En la dirección x:
33
/500)
8,9
9,4
(/1000 mkgmkg
g
a
x
P x




En la dirección y:
33
/1500)
8,9
9,4
1(/1000)1( mkgmkg
g
a
y
P y




dy
y
P
dx
x
P
dP






dydxdP 1500500 

9. Para un punto en la superficie libre del fluido:
3
1
0 
dx
dy
dP
Pendiente de las
líneas de igual
presión
(SUPERFICIES)
Como: dydxdP 1500500 
Integrando de Po a P, de 0 a x, y
de 0 a y tenemos:
yxPP 15005000

Para un punto en la superficie del
fluido P=0
Entonces para (x,y)=(1,2 m , 0,7 m) la presión es cero P=0 , de la ecuación anterior
se obtiene: 2
00
/1650)70,0(1500)20,1(5000 mkgPP 
Con este valor de Po, yxmkgP 1500500/1650
2

Esta ecuación da el valor de la presión en cualquier punto en el interior del fluido

10. Presión A (0 , 1,20 m). El fluido no alcanza
este punto 0 A
P
Presión en el punto B (0 , 0)
2
/1650 mkgPB

Presión en el punto C (1,2 m , 0)
)2,1(/500/1650
32
mmkgmkgPC

2
/1050 mkgPC


11. - La superficie libre del fluido adopta forma
paraboloide de revolución
- Un plano vertical x origen corta superficie libre
según una parábola
- Ecuación de la parábola (vértice en el origen)
5.4 Mov Rotación ( Recipientes Abiertos)
y =
w2x2
2g

12. - Al girar los recipientes aumenta la presión
- Incremento presión entre un punto situado en
el eje y otro en el mismo plano horizontal pero
a una distancia x es
5.4 Mov Rotación ( Recipientes Cerrados)
p = 
w2x2
2g
p

= 𝑦 =
w2x2
2g

13. MOVIMIENTO DE ROTACIÓN
Recipientes abiertos
Recipientes cerrados
Sin presión adicional
Con presión adicional
Coordenadas cilíndricas
dz
z
P
d
P
dr
r
P
dP








 q
q
Para el elemento diferencial
  0H
F

0)( 


 madAdr
r
P
PPdA
0)()(
2



 rdAdr
g
dAdr
r
P
PPdA w


14. Entonces: r
gr
P 2
w




y g
z
P
 


dz
z
P
d
P
dr
r
P
dP








 q
q
Pero
0


q
P
gdzrdrdP w 
2
Integrando: Cgz
r
P  
w
2
22
Si r=0, z=zo; P=Po 00
gzPC 
22
00
2
1
)( rzzgPP w 

15. En la superficie libre del fluido P=Po obtiene la
ec de la forma de la superficie y de la forma de
las superficies de igual presión
22
000
2
1
)( rzzgPP w 
De donde:
g
r
zz
2
22
0
w

ECUACIÓN DE UN
PARABOLOIDE DE
REVOLUCIÓN
Las superficies de igual presión son
paraboloides de revolución

16. Volumen paraboloide de revolución es la mitad
del volumen del cilindro circunscrito a dicho
paraboloide.
a) Eje de giro está fuera del recipiente:
Parte del paraboloide se forma dentro del
recipiente.
b) El recipiente se tapa sin añadir presión:
El paraboloide se considera sobre la tapa
del recipiente tangente a ella

17. c) El recipiente se tapa
añadiendo presión
adicional: Esta se
considera como una
altura sobre la tapa del
recipiente; sobre dicho
nivel se forma el
paraboloide.

18. EJEMPLO. Un depósito de forma cilíndrica de
4 m de altura y 2 m de diámetro contiene
aceite hasta 3,2 m de altura. A cuantas rpm
debe girar el recipiente alrededor de su eje
para que el aceite alcance el borde superior?
Volumen paraboloide = Volumen cilindro /2
r
gh
h
g
r
z
2
2
22
 w
w
srad
m
msm
/96,3
1
)8,0)(/81,9(2
2
 w

19. rpm
s
rad
rev
srad

w
2
60
96,3)
60
min1
2
1
)(/96,3( 
rpm83,37w
EJEMPLO:
Un cilindro de 1,8 m de diámetro y 2,70 m de altura
se llena completamente con glicerina de densidad
1,60 y al taparlo se añade al depósito una presión
de 2,50 kg/cm². El material de que está hecho el
cilindro tiene 13 mm de espesor con un esfuerzo
admisible de trabajo de 850 kg/cm². Determinar a
qué velocidad máxima se puede hacer girar el
recipiente sobres su eje sin que se rompa.
SOLUCIÓN:
El esfuerzo tangencial en un cilindro de radio r, con presión interna P es:
t
Pr
 t es el espesor del material de
que está hecho el cilindro
De la figura se puede deducir que la presión será máxima en el borde inferior
externo del cilindro

20. 2
2
/3,12
90
)3,1)(/850(.
cmkg
cm
cmcmkg
r
t
P 

La presión que puede soportar el recipiente será:
2222
2
1
/50,2/3,12 rg
g
cmkghcmkg w 
Con la configuración del problema:
Reemplazando los datos del problema:
)8100()/6,1(
2
1
/5,2)270(/6,1/3,12
223232
cmcmgrcmkgcmcmgrcmkg w
rpmsrad 363/38 w
De donde se obtiene

21. En el caso de las bombas y turbinas la
rotación de una masa en un fluido, o en
caso que gire el recipiente que lo contiene,
se genera un incremento en la presión
entre un punto situado en el eje y uno a
una distancia X del eje en el mismo plano
horizontal; y esta dada por :Y el aumento
de la altura de presión será Que es una
ecuación parecida a la aplicable a
recipientes abiertos en rotación. La
velocidad lineal Vy el termino da la altura
de velocidad.