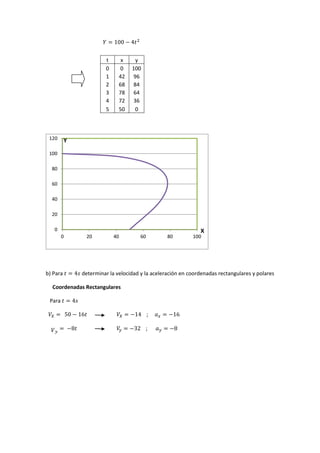
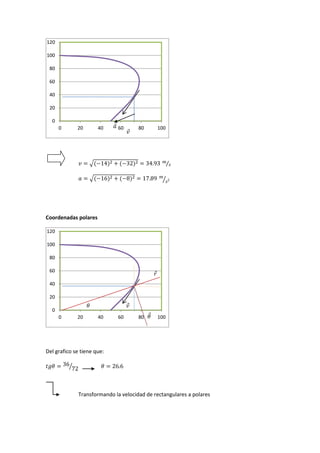
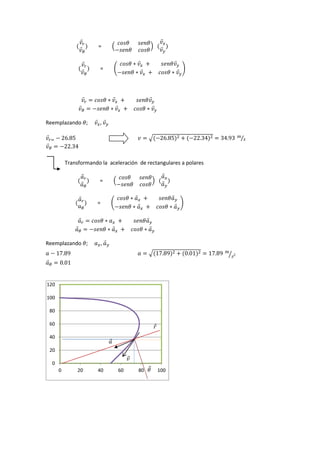
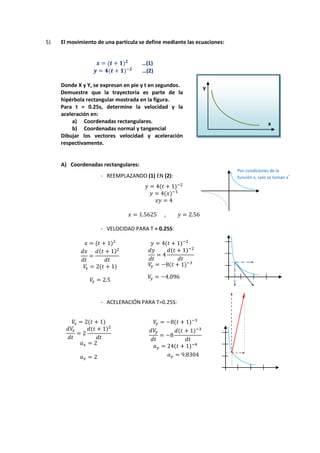
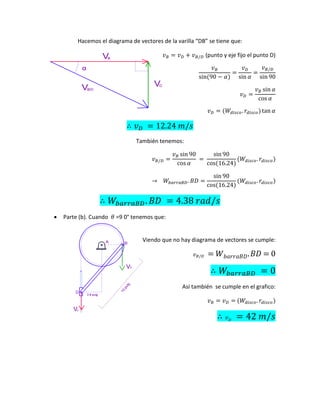
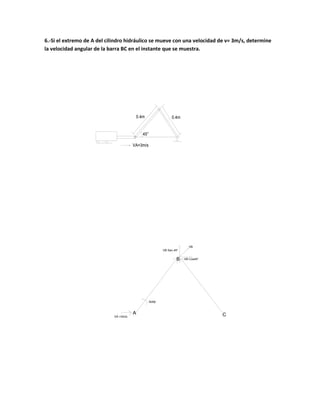
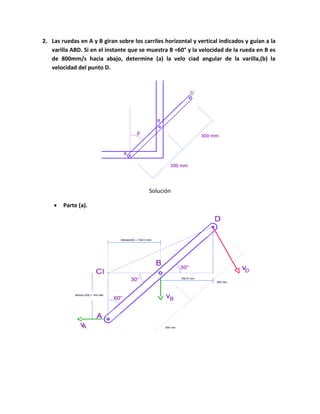
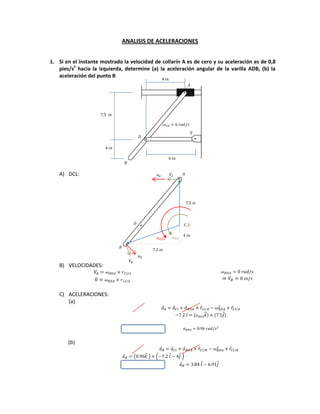
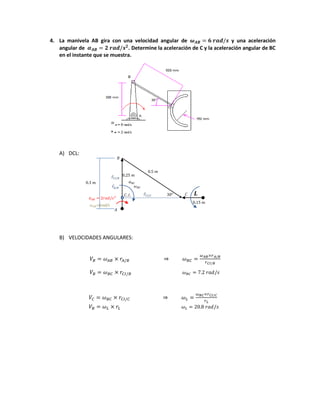
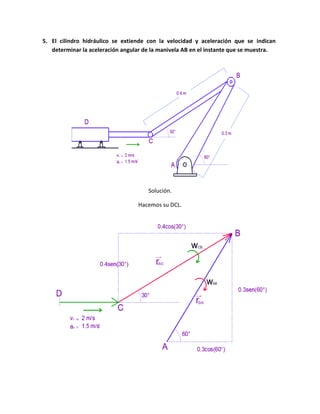
El documento describe diversas situaciones de cinemática aplicada a partículas y varillas en movimiento, abordando el cálculo de velocidad, aceleración y trayectoria a través de ecuaciones matemáticas. Se incluyen problemas sobre partículas en trayectorias rectilíneas y circulares, así como el análisis de cuerpos en movimientos guiados por pasadores y varillas. A lo largo del texto, se utilizan herramientas de cálculo integral y transformaciones de coordenadas para resolver las dinámicas de los sistemas propuestos.

1. Dinámica
U N I V E R S I D A D N A C I O N A L
D E L S A N T A
I N G E N I E R Í A C I V I L
V C I C L O
Campos Guerra Carlos
Fournier Pais Analí
Jimenez Gonzales Margarita
Sánchez Lizárraga Juan
Terrones López Yessenia
Torres Lara María Victoria

2. PRÁCTICA N°1 – CINEMÁTICA PUNTUAL
1. Una partícula se desplaza a través de un fluido siguiendo una trayectoria
rectilínea. La aceleración de la partícula está definida por la función a=-kv.
Donde k es una constante, v en m/s2
. Cuando x=0, v=v0, deducir las expresiones de
la velocidad y la posición en función del tiempo.
a) Se tiene la ecuación del tipo entonces se utilizará:
∫ ∫
∫ ∫
∫ ∫
∫ ∫

3. b) 2. A partir de X=0 sin velocidad inicial, una partícula recibe una aceleración
√ , donde “a” y ”v” se expresan en pie/s2
y pie/s respectivamente.
Determine:
a). La posición de la partícula cuando V = 24 pie/s.
b). La velocidad de la partícula cuando X = 40 pie.
a). x = 0 → v = 0 , x = ? → v = 24 pie/s.
√ , a ɗs = v ɗv
∫ √ ∫
∫ ∫ √
Haciendo u = v2
+ 49 → ɗu = 2v
∫ ∫
√
→ 2 (0.8) x = 2 (u1/2
]
0.8 x =√ → X = 6.12 pie
b). x = 0 → v = 0 , x = 40 pie → v = ?
√ , a ɗs = v ɗv
∫ √ ∫
∫ ∫ √
Haciendo u = v2
+ 49 → ɗu = 2v
∫ ∫
√
→ 2 (0.8) (40) = 2 (u1/2
]
32 = √ → V= 1024 pie/s

4. P4 El movimiento de una partícula está definida por
Donde , , se expresan en ⁄ y m respectivamente. Cuando ,
a) Dibujar la trayectoria de la partícula durante el intervalo de 5s
b) Para determinar la velocidad y la aceleración en coordenadas rectangulares
y polares
c) Dibujar los vectores, velocidad y aceleración correspondiente.
Solución:
Sabemos que ; reemplazando del problema e
integrando se tiene que:
∫ ∫
Si entonces: si entonces
DATOS
;
;
a) Dibujar la trayectoria de la partícula durante el intervalo de 5s
Si

5. b) Para determinar la velocidad y la aceleración en coordenadas rectangulares y polares
Coordenadas Rectangulares
Para
;
;
0
20
40
60
80
100
120
0 20 40 60 80 100
t x y
0 0 100
1 42 96
2 68 84
3 78 64
4 72 36
5 50 0
X
Y

6. √ ⁄
√ ⁄
Coordenadas polares
Del grafico se tiene que:
⁄
Transformando la velocidad de rectangulares a polares
0
20
40
60
80
100
120
0 20 40 60 80 100
0
20
40
60
80
100
120
0 20 40 60 80 100
⃗
⃗
⃗
⃗
⃗

7. ⃑
⃑
= ( )
⃑
⃑
⃑
⃑
= (
⃑ ⃑
⃑ ⃑
)
⃑ ⃑ ⃑
⃑ ⃑ ⃑
Reemplazando ⃑ ⃑
⃑ √ ⁄
⃑
Transformando la aceleración de rectangulares a polares
⃑
⃑
= ( )
⃑
⃑
⃑
= (
⃑ ⃑
⃑ ⃑
)
⃑ ⃑
⃑ ⃑ ⃑
Reemplazando ⃑
√ ⁄
⃑
0
20
40
60
80
100
120
0 20 40 60 80 100
⃗
⃗
⃗
⃗

8. 5) El movimiento de una partícula se define mediante las ecuaciones:
…(1)
…(2)
Donde X y Y, se expresan en pie y t en segundos.
Demuestre que la trayectoria es parte de la
hipérbola rectangular mostrada en la figura.
Para t = 0.25s, determine la velocidad y la
aceleración en:
a) Coordenadas rectangulares.
b) Coordenadas normal y tangencial
Dibujar los vectores velocidad y aceleración
respectivamente.
A) Coordenadas rectangulares:
- REEMPLAZANDO (1) EN (2):
- VELOCIDAD PARA T = 0.25S:
- ACELERACIÓN PARA T=0.25S:
y
x
Por condiciones de la
función x, solo se toman x
+

9. 6. Una partícula se mueve a lo largo de una trayectoria circular de radio r. La longitud del arco
recorrido en el tiempo es S= . Determine los componentes de la aceleración de la partícula
como funciones del tiempo.
- Del gráfico se deduce:
S=r 
- Hallamos ̇ ̈ ̇ ̈ :
o Como es una trayectoria circular, r es constante y por ende:
 ̇
 ̈
o En caso de :
 ̇ =
 ̈
- Para hallar la aceleración, hallamos sus componentes radial y transversal:
o ̈ ̇
o ̈ ̇ ̇
- Entonces hallando la aceleración:
o √
√

10. √
√
- De esa forma obtenemos la aceleración en función del tiempo.

11. 7. Una partícula se mueve a lo largo de una trayectoria circular de radio r=400mm. Su
posición en función del tiempo esta dada por: 2t2
y t están en radianes y segundos
respectivamente.
Cuando 60°, determinar la velocidad y la aceleración en coordenada polares y
coordenadas rectangulares.
Dibujar los vectores velocidad y aceleración respectivamente
Datos del problema
r=400mm
2t2
Cuando
60
a) b)
En coordenadas polares:
Hallando el tiempo para 60
60 2t2
T=0.72s
Hallando
a) =d /dt
2t2
/dt
para t= 0.72 s
= 2.88 rad/s
b) =d /dt
rad/s2
En coordenadas Polares
X= rcos60°
X= 400mm.cos60°
X= 200mm
Y= rsen60°
Y= 400mm.sen60°
Y=346.41mm
X=400cos(2t2
)
x°= - 400sen(2t2
).4t

12. Y= 400sen(2t2
)
Y°=400cos(2t2
).4t
V= ( ( x°)2
+(Y°)2
)1/2
V= ( (- 400sen(2t2
).4t)2
+(400cos(2t2
).4t)2
)1/2
V= (1600.16.t2
.sen2
(2t2
)+1600.16t2
cos2
(2t2
))1/2
V=400(4t) para t= 0.72s
V= 1152 m/s
Hallando la aceleracion
X°°= -400(d(sen(2t2
)/dt).4t +(400.sen(2t2
)).d(4t)/dt
X°° = -400cos(2t2
). 16t2
+.sen(2t2
).4
Y°°= 400d(cos(2t2
))/dt).4t + 400cos(2t2
).d(4t)/dt
Y°° = (- 400sen(2t2
). 16t2
) +cos(2t2
).4
a = ( ( x°°)2
+(Y°°)2
)1/2
a =( (-400cos(2t2
). 16t2
+.sen(2t2
).4)2
+ (- 400sen(2t2
). 16t2
) +cos(2t2
).4)2
)1/2
a= 20(8t)((cos(2t2
). sen(2t2
))1/2
para t=0.72s
a=15.49 m/s2

13. A
B
500 mm.
15°
15°
V r
v
B
500 mm.
500 sen40° i
-500 sen50° j
= 150 mm/s
A
B
A
B/A40°
CINEMÁTICA PLANA: Análisis de Velocidades
1. El movimiento de la varilla AB es guiado por los pasadores puestos en A y B, los cuales se
deslizan en las ranuras indicadas. En el instante mostrado, Ө = 40° y el pasador en B se
mueve hacia arriba y a la izquierda con velocidad constante de 150mm/s. Determine (a)
la velocidad angular de la varilla, (b) la velocidad del pasador en el extremo A.
VB = VA + ωAB x rB/A
( -150 i + 150 j ) = VA j + ωAB k x ( 500 i – 500 j)
( -150 i + 150 j ) = VA j + - 500 ωAB j + 500 ωAB i
i: -150 = 500 ωAB …………………………………………..(1)
j: 150 = VA + - 500 ωAB ………………………………….(2)
EN (1):
ωAB =
ωAB = - 0.378 rad/s
ωAB = 0.378 rad/s
EN (2):
150 = VA + - 500 ωAB
VA = 150 + 500 x ( )
VA = 160.39 mm/s

14. 2.- El collarín D se desliza por una varilla vertical fija. Di el disco tiene velocidad angular
constante de 15 rad/s en el sentido de las manecillas del reloj, determine la aceleración
angular de la barra BD y la aceleración del collarín D cuando (a) = 0°, (b) =9 0°, (c)
=180 0°.
Solución:
Sabemos que:
 Parte (a). Cuando = 0° tenemos que:
( )
Luego:

15. Hacemos el diagrama de vectores de la varilla “DB” se tiene que:
(punto y eje fijo el punto D)
También tenemos:
 Parte (b). Cuando =9 0° tenemos que:
Viendo que no hay diagrama de vectores se cumple:
Así también se cumple en el grafico:

16. 3) la barra AB gira en sentido contrario a las manecillas del reloj y en el instante mostrado la
magnitud de la velocidad del punto G es de 25 m/s. determinar la velocidad angular de cada uno
de las tres barras para este instante.
Analizando la barra AB
……………..(1)
Analizando la barra BGD
⃑
=
+
⃑
⁄
DIAGRAMA DEL VECTOR VELOCIDAD
A
B
G
⃑
⃑
⃑
B
⃑
⃑
⁄
⁄
⁄

17. por ser un triangulo equilátero se tiene que :
⁄
=
⁄ ⁄ =0.09
⁄ Diagrama del vector
Aplicando ley de cosenos
⁄ ⁄
=
=16.04rad/s
=16.04rad/s
=16.04rad/s
⃑

18. 4. Si la velocidad angular del eslabón CD es , determine la velocidad del punto
E en el eslabón BC y la velocidad angular del silaben AB en el instante que se muestra.
A) DCL:
B) Velocidades:
⃑⃑ ⃑⃑ ⃑⃑⃑ ⃑
⃑⃑ ( ⃑⃗) ⃗
⃑⃑ ⃗
⃑⃑ ⃑⃑ ⃑⃑⃑ ⃑
⃑⃑ ⃗ ( ⃑⃗) ⃗
⃑⃑ ⃗ ⃗
⃑⃑ ⃑⃑ ⃑⃑⃑ ⃑
⃑⃑ ( ⃑⃗)( √ ⃗ ⃗)
⃑⃑ ⃗ ⃗
Igualando componentes de (1) y (2):
⃗
⃗
Hallando V en E:
⃑⃑ ⃑⃑ ⃑⃑⃑ ⃑
⃑⃑ ⃗ ( ⃑⃗) ⃗
⃑⃑ ⃗ ⃗
√
⃗
⃗
⃗

19. 5. Si al centro O del engrane se le imprime una velocidad de 10 m/s determine la
velocidad del bloque corredizo B en el instante que se muestra.
- D C L:
- Como el movimiento es regular tenemos:
VA = VO + ωOA x rA/O
VA = 10 i - ωOA k x 0.125 j
VA = 10 i + 0.125 ωOA i
- Como no tenemos ningún otro dato que nos ayude al análisis de velocidades, nos
apoyamos con el centro instantáneo de velocidad cero, que viene a encontrarse en el
punto de contacto entre el engrane y la
cremallera.
VO = ωOA . rCI/O
10 = ωOA x (0.175)
ωOA = 57.14
- Reemplazamos:
VA = 10 i + 0.125 (57.14) i = 17.14 i
- Para la velocidad en B:
VB = 17.14 i + ωAB x rB/A
VB = 17.14 i + ωAB k x (0.6 cos30° i – 0.6 sen30° j)

20. VB = 17.14 i + 0.6 cos30° ωAB j + 0.6 sen30° ωAB i
VB cos60° i + VB sen60° j = (17.14 + 0.6 sen30° ωAB) i + 0.6 cos30° ωAB j
 VB sen60° = 0.6 cos30° ωAB …………..(1)
ωAB =0.6 VB
 VB cos60° = 17.14 + 0.6 sen30° ωAB
VB cos60° = 17.14 + 0.6 sen30° (0.6 VB)
VB =53.6

21. 6.-Si el extremo de A del cilindro hidráulico se mueve con una velocidad de v= 3m/s, determine
la velocidad angular de la barra BC en el instante que se muestra.
0.4m 0.4m
45°
VA=3m/s
VB Cos45°
VB Sen 45°
VB
VA =3m/s
A
B
C
WAB

22. VB = VA + AB x rB/A
VBsen45°j + VBcos45°i = 3i + ABk(0.4sen45°j + 0.4cos45°i
VBsen45°j + VBcos45°I = 3I + ABsen45°(0.4i) + ABcos45°(0.4j)
I:
VBcos45°= 3 - ABsen45° …….(1)
J:
VBsen45 = ABcos45°(0.4)
VB= 0.4 AB………(2)
(1 ) en (2)
0.4 ABcos45°= 3 - ABsen45°
AB = 5.30 rad/s
VB = 2.12m/s
VB = VC + CB x rB/C
2.12x√ j + 2.12x√ I = 0 + CB-k(-0.4sen45°I + 0.4cos45°J)
2.12x√ j + 2.12x√ I = CB0.4sen45°I + CB 0.4cos45°J
I:
2.12x√ = CB0.4sen45°
CB = 5.3 rad/s2

23. A
B
E
D
200 mm.
250 mm.
200 mm.
600 mm.
D E C.I
B
A
0.6 m
0.25 m
O.2 m
CENTRO INSTANTÁNEO DE VELOCIDAD CERO
1. En el instante mostrado la velocidad angular de la varilla AB es de 15 rad/s en el
sentido de las manecillas del reloj, determine (a) la velocidad angular de la varilla
BD, (b) la velocidad del collarín D, (c) la velocidad del punto A.
EN AB:
VB = ωAB . R
VB = (15 rad/s)(0.2m)
VB = 3 m/s
EN BD:
VB = ωBD . rCI/B
3 m/s = ωBD . (0.25m)
ωBD = 12 rad/s
VD = ωBD . rCI/D
VD = (12 rad/s)(06m)
VD = 7.2 m/s

24. 2. Las ruedas en A y B giran sobre los carriles horizontal y vertical indicados y guían a la
varilla ABD. Si en el instante que se muestra B =60° y la velocidad de la rueda en B es
de 800mm/s hacia abajo, determine (a) la velo ciad angular de la varilla,(b) la
velocidad del punto D.
Solución
 Parte (a).

25. Tenemos que debe cumplirse que:
Luego:
√
 Parte (b)
Del grafico anterior se cumple que:
√ Luego:
√ √

26. 3) en el instante en que se indica la velocidad angular de la barra DE de 8rad/s en sentido
contrario al de las manecillas del reloj. Determine a) la velocidad angular de la barra BD, b) la
velocidad angular de la barra AB, c) la velocidad del punto medio de la barra BD
UBICANDO EL CENTRO INSTANTANEO
De la barra DE:
De la barra AB:
X=41.569pulg
Y=24pulg
Sabemos que: ley de senos
19.1
m
=253.99pulg/s
ley de cosenos para el triangulo CMD
m=31.749 pulg
⃑m

27. ANALISIS DE ACELERACIONES
1. Si en el instante mostrado la velocidad de collarín A es de cero y su aceleración es de 0,8
pies/s2
hacia la izquierda, determine (a) la aceleración angular de la varilla ADB, (b) la
aceleración del punto B
A) DCL:
B) VELOCIDADES:
C) ACELERACIONES:
(a)
⃗ ⃗ ⃗ ⃗ ⃗
⃗ ⃑⃗ ⃗
(b)
⃗ ⃗ ⃗ ⃗ ⃗
⃗ ( ⃑⃗ ) ( ⃗ ⃗ )
⃗ ⃗ ⃗

28. 3.- Si en el instante en que se indica la barra DE tiene velocidad angular constante de 18 rad/s
en el sentido de las manecillas del reloj, determine la aceleración angular de la barra BGD y la
aceleración angular de la barra DE.
A
4in.
15.2in. 4in.
4in.
B
D
C
E

29. A
B
D E
VB
VD
C.I
4in15.2in
8in
8in
C
18rad/s
VD = BD x rCI/D ........(1)
VB = BD x rCI/B ........(2)
Igualando BD :
VD = VB ………(3)
rCI/D rCI/B
VD = DEx rD/B
VD = 18 rad/s(15.2in)
VD = 273.6in/s

30. Hallando (3)
VB = VD (rCI/B ) = 273.6 in/s(8in) =112.82 in/s
rCI/D 19.2in
Hallando (2)
112.82in/s = BD(8in)
BD = 14.10rad/s
VB = AB (rA/B)
AB = 112.82 in/s = 14.10rad/s
8in
SI:
AB = BD
rA/B = rB/D
ENTONCES.
AB = BD
aB = aA + ABxrB/A – A/B)2
x rA/B
aB = 0 + AB k(-8j)– )2
x(-8j)
aB = AB (8i)– (1590.48j)
aD = aE + EDxrED– E/D)2
x rD/E
aD = 0 + (-15.2i)(- EDk) -182
(-15.2i)
aD = 15.2 EDj + 4924.8i………(4)
aB = aD + BDxrB/D – B/D)2
x rB/D
Reemplazamos en aB el aD
aB = 15.2 EDj + 4924.8i + BDk(19.2i + 8j) – B/D)2
(19.2i + 8j)
aB = 15.2 EDj + 4924.8i + BD19.2j –( BD 8i) – )2
(19.2i + 8j)
aB = 15.2 EDj - 1590.49j + BD19.2j – BD 8i) + 1107.65i

31. Igulando aB :
AB (8i)+ (1590.49j) = 15.2 EDj - 1590.49j + BD19.2j – BD 8i) + 1107.65i
I:
AB (8) =1107.65 - BD (8)
Sabemos que:
AB = BD
BD (16)= 1107.65
BD = 69.22 rad/s2
AB = 69.22 rad/s2
J:
1590.49= 15.2 ED - 1590.49+ BD19.2
3180.98 = 15.2 ED + 19.2(69.22)
ED = 121.83 rad/s2

32. 4. La manivela AB gira con una velocidad angular de y una aceleración
angular de . Determine la aceleración de C y la aceleración angular de BC
en el instante que se muestra.
A) DCL:
B) VELOCIDADES ANGULARES:
=6rad/s
⃗
⃗
⃗

33. C) ACELERACION Y ACELERACION ANGULAR
⃗ ⃗ ⃗ ⃗ ⃗
⃗ ⃗ ⃗ ⃗ ⃗
⃗ ⃗ ⃗ ⃗
⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
( ⃑⃗) ⃗ ⃗ ( ⃑⃗) ⃗ ⃗ ⃗
( ⃑⃗) ⃗ ⃗
⃗ ⃗
⃗ ⃗ ⃗ ⃗
⃗ ⃗ ⃗
⃗

34. 5. El cilindro hidráulico se extiende con la velocidad y aceleración que se indican
determinar la aceleración angular de la manivela AB en el instante que se muestra.
Solución.
Hacemos su DCL.

35.  Analizamos las velocidades.
Tenemos que: luego:
 En el tramo CB tenemos:
√ ……………(1)
 En el tramo AB tenemos:
√ ……………….. (2)
Igualamos las ecuaciones (1) y (2)
√ = √
De donde encontramos los resultados:
… El signo negativo indica que la velocidad esta
en sentido horario.
… El signo negativo indica que la velocidad
esta en sentido horario.
 Analizamos las aceleraciones.
 En el tramo CB tenemos: –
√ √ ………(3)
 En el tramo AB tenemos: –
√ √ ………(4)

36. Igualamos las ecuaciones (1) y (2)
( √ ) ( √ ) √ √
De donde obtenemos los valores: