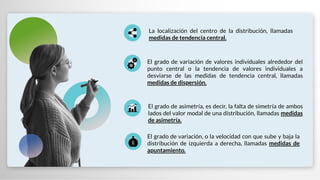
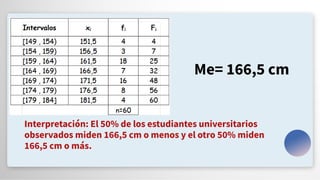
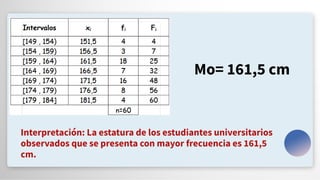
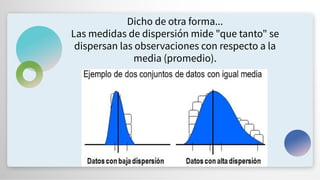
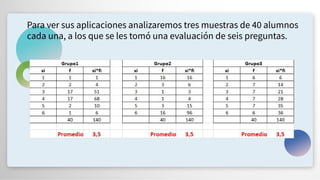
El documento presenta un repaso sobre estadística descriptiva y visualización de datos, destacando la importancia de la comunicación visual y herramientas como el visual thinking. Se abordan conceptos clave como medidas de tendencia central (media, mediana y moda) y medidas de dispersión (rango, varianza y desviación estándar), junto con sus ventajas y desventajas. También se menciona cómo compartir y visualizar datos de manera efectiva utilizando plataformas digitales.

1. Veremos un pequeño repaso y otras
cuestiones nuevas para ustedes...
ESTADÍSTICA

2. DESCRIPCIÓN DE
UN CONJUNTO DE
DATOS: MÉTODOS
NUMÉRICOS

3. GASTOS
INGRESOS
Hemos visto que los datos de
una muestra pueden ser
representados grá camente
Grá cos
Si se desea describir más profundamente el conjunto
de datos no siempre es fácil hacerlo a partir de un
gráfico

4. La comunicación visual es una herramienta clave. Nos resulta más
sencillo 'leer' imágenes, que leer un texto escrito. Por ello,
disciplinas como el Visual Thinking facilitan la toma de notas
visualmente ricas gracias al uso de imágenes, grá cas, infografías
y dibujos sencillos.
La comunicación visual es una herramienta clave. Nos resulta más
sencillo 'leer' imágenes, que leer un texto escrito. Por ello,
disciplinas como el Visual Thinking facilitan la toma de notas
visualmente ricas gracias al uso de imágenes, grá cas, infografías
y dibujos sencillos.

5. Q1 Q2 Q3 Q4 TOTAL
INGRESOS 1,700.000 1,800.000 1,790.000 1,700.000 46,000.000
GASTOS 1,800.000 2.017.000 2,000.000 1,900.000 52,000.000
Tablas de frecuencias
Vimos que podíamos reducir los datos a una forma
más compacta, comprensible y comunicable por la
distribución de frecuencias.

6. Q1 EN. FEB. MAR. TOTAL
INGRESOS
Item 1 50.000 17.000 22.689 2,800.000
Item 2 7.000 11.500 15.000 5,000.000
Item 3 20.000 228 20.000 10,000.000
Item 4 249 24.050 24.089 6,000.000
TOTAL 1,700.000 1,800.000 1,790.000 46,000.000
GASTOS
Item 1 17.000 38.000 17.300 5,900.000
Item 2 11.500 17.000 5.000 15,000.000
Item 3 228 11.500 49.000 2,800.000
Item 4 24.050 228 1.000 5,000.000
TOTAL 1,800.000 2.017.000 2,000.000 52,000.000

7. Q3 JUL. AGO. SEP TOTAL
INGRESOS
Item 1 50.000 17.000 22.689 2,800.000
Item 2 7.000 11.500 15.000 5,000.000
Item 3 20.000 228 20.000 10,000.000
Item 4 249 24.050 24.089 6,000.000
TOTAL 1,700.000 1,800.000 1,790.000 46,000.000
GASTOS
Item 1 17.000 38.000 17.300 5,900.000
Item 2 11.500 17.000 5.000 15,000.000
Item 3 228 11.500 49.000 2,800.000
Item 4 24.050 228 1.000 5,000.000
TOTAL 1,800.000 2.017.000 2,000.000 52,000.000

8. Q4 OCT. NOV. DIC. TOTAL
INGRESOS
Item 1 50.000 17.000 22.689 2,800.000
Item 2 7.000 11.500 15.000 5,000.000
Item 3 20.000 228 20.000 10,000.000
Item 4 249 24.050 24.089 6,000.000
TOTAL 1,700.000 1,800.000 1,790.000 46,000.000
GASTOS
Item 1 17.000 38.000 17.300 5,900.000
Item 2 11.500 17.000 5.000 15,000.000
Item 3 228 11.500 49.000 2,800.000
Item 4 24.050 228 1.000 5,000.000
TOTAL 1,800.000 2.017.000 2,000.000 52,000.000

9. Q2 ABR. MAY. JUN. TOTAL
INGRESOS
Item 1 50.000 17.000 22.689 2,800.000
Item 2 7.000 11.500 15.000 5,000.000
Item 3 20.000 228 20.000 10,000.000
Item 4 249 24.050 24.089 6,000.000
TOTAL 1,700.000 1,800.000 1,790.000 46,000.000
GASTOS
Item 1 17.000 38.000 17.300 5,900.000
Item 2 11.500 17.000 5.000 15,000.000
Item 3 228 11.500 49.000 2,800.000
Item 4 24.050 228 1.000 5,000.000
TOTAL 1,800.000 2.017.000 2,000.000 52,000.000

10. En realidad, raras veces
observamos o medimos
poblaciones enteras, por
esto, nos dedicaremos a la
descripción de conjuntos de
datos, en términos de
muestras.

11. ¿Sabías que Genially te permite compartir tu
creación directamente, sin necesidad de
descargas? Listo para que tu público pueda
visualizarlo en cualquier dispositivo y darle
difusión en cualquier lugar.

12. Las características muestrales
permiten caracterizar a una muestra
con unos pocos valores, llamados
estadísticos.
Si bien cualquiera función de n
observaciones de una muestra es una
estadística, hay algunas que son
especialmente interesantes. En
términos del análisis de datos, nos
interesaremos por cuatro:

13. El grado de variación, o la velocidad con que sube y baja la
distribución de izquierda a derecha, llamadas medidas de
apuntamiento.
El grado de variación de valores individuales alrededor del
punto central o la tendencia de valores individuales a
desviarse de las medidas de tendencia central, llamadas
medidas de dispersión.
El grado de asimetría, es decir, la falta de simetría de ambos
lados del valor modal de una distribución, llamadas medidas
de asimetría.
La localización del centro de la distribución, llamadas
medidas de tendencia central.

14. Medidas de tendencia central
Las medidas de tendencia central suelen llamarse
promedios, y son el ʻvalor típicoʼ en el sentido de que se
emplea a veces para representar todos los valores
individuales de un conjunto de datos.
La tendencia central de un conjunto de datos es la
disposición de éstos para agruparse ya sea alrededor del
centro o de ciertos valores numéricos.
Las más frecuentemente utilizadas son la media
aritmética, la mediana y la moda.

15. La media aritmética de las observaciones x1, x2, ..., xn es el promedio
aritmético de éstas.
La media aritmética es el valor que tomaría la variable si estuviera
uniformemente repartida entre todos los individuos que forman la
muestra (corresponde al concepto de centro de gravedad en Física).
La media aritmética considera todos los datos. Sin embargo, debido a
que todas las observaciones se emplean para el cálculo, el valor de la
media puede afectarse de manera desproporcionada por la existencia
de valores extremos.
Cuando usemos el término media, nos referimos a la media aritmética
o promedio.

16. Ventajas

17. & Se trata de un concepto familiar para la mayoría de las
personas y es intuitivamente claro.
& Cada conjunto de datos numéricos tiene media; siendo
ésta una medida que puede calcularse y es única, debido a
que cada conjunto de datos posee una y sólo una media.
& La media es útil para llevar a cabo procedimientos
estadísticos como la comparación de medias de varios
conjuntos de datos.

18. Desventajas

19. Aunque la media es con able en el sentido de que
toma en cuenta todos los valores del conjunto de
datos, puede verse afectada por valores extremos
que no son representativos del resto de los datos.
El cálculo se hace tedioso cuando trabajamos con una
gran cantidad de valores diferentes.
Se presentan dudas al calcular la media para clases
de extremo abierto, tales como, “mayor que 14” o
“menor que 6”.

20. La mediana es, como su nombre
lo indica, el valor medio o valor
central de un conjunto de
observaciones.
Cuando todas las
observaciones se ordenan en
forma creciente, la mitad de
éstas es menor que este valor y la
otra mitad es mayor.

21. Ventajas

22. & Si un conjunto contiene valores extremos y un número alto de
observaciones, la mediana puede ser una medida de tendencia
central mucho más deseable que la media aritmética.
& Los valores extremos no afectan a la mediana tan intensamente
como a la media.
& La mediana es fácil de entender y se puede calcular a partir de
cualquier tipo de datos (excepto datos cualitativos nominales),
incluso a partir de datos agrupados con clases de extremo abierto, a
menos que la clase mediana sea justamente una de las de extremo
abierto, por ejemplo, la clase “mayor que 4”.

23. Desventajas

24. Ciertos procedimientos estadísticos que utilizan la
mediana son más complejos que aquellos que utilizan
la media.
Debido a que la mediana es una posición promedio,
debemos ordenar los datos antes de llevar a cabo
cualquier cálculo, lo cual consume mucho tiempo si el
conjunto de datos es muy grande.

25. Moda
La moda, modo o valor modal de un conjunto de observaciones es el valor
de las observaciones que ocurre con mayor frecuencia en el conjunto.
El modo es la única medida de tendencia central que puede ser
calculada para variables cualitativas nominales.
Puede suceder que en una serie de datos haya más de una moda. En
tal caso se denomina bimodal, trimodal o multimodal, según el
número de modas que presente.

28. La mediana es el
valor promedio
entre 167 cm y
168 cm, es decir:
Me= 167,5 cm
Interpretación: El 50% de los estudiantes universitarios
observados miden 167,50 cm o menos y el otro 50% miden
167,50 cm o más.

29. Para el cálculo de la
moda, basta con buscar el
valor de la variable que
presente la máxima
frecuencia. Entonces, la
moda es: Mo= 160 cm
Interpretación: La estatura de los estudiantes universitarios
observados que se presenta con mayor frecuencia es 160 cm.

32. Me= 166,5 cm
Interpretación: El 50% de los estudiantes universitarios
observados miden 166,5 cm o menos y el otro 50% miden
166,5 cm o más.

33. Mo= 161,5 cm
Interpretación: La estatura de los estudiantes universitarios
observados que se presenta con mayor frecuencia es 161,5
cm.

36. MEDIDAS DE
DISPERSIÓN

37. Las medidas de tendencia central nos indican
los valores alrededor de los cuales se
distribuyen los datos.
Las medidas de dispersión nos proporcionan
una medida del mayor o menor agrupamiento
de los datos respecto a los valores de
tendencia central. Todas ellas son valores
mayores o iguales a cero, indicando un valor
cero, la ausencia de dispersión.

38. Dicho de otra forma...
Las medidas de dispersión mide "que tanto" se
dispersan las observaciones con respecto a la
media (promedio).

39. Para ver sus aplicaciones analizaremos tres muestras de 40 alumnos
cada una, a los que se les tomó una evaluación de seis preguntas.
Los xi indican el
número de
respuestas
correctas y fi,
indica la cantidad
de alumnos que lo
hicieron.

40. Para ver sus aplicaciones analizaremos tres muestras de 40 alumnos
cada una, a los que se les tomó una evaluación de seis preguntas.

41. Las tres distribuciones tienen la misma media aritmética, 3,5
puntos, ¿pero podemos afirmar que hay homogeneidad
entre los grupos?.
Gráficamente vemos que el valor de la media aritmética no
es suficiente para describir cada una de las situaciones. Para
precisar mejor lo que denominamos como ʻdispersiónʼ
podemos calcular unos estadísticos que nos den
información, sin necesidad de representar los datos.
El rango,
La varianza
La desviación típica
El coeficiente de variación
son las medidas de dispersión más conocidas.

42. Las medidas de dispersión son números que indican si una
variable se mueve mucho, poco, más o menos que otra. La
razón de ser de este tipo de medidas es conocer de manera
resumida una característica de la variable estudiada.
En este sentido, deben acompañar a las medidas de tendencia
central. Juntas, ofrecen información de un sólo vistazo que
luego podremos utilizar para comparar y, si fuera preciso,
tomar decisiones.

43. Rango
Es la diferencia entre el mayor y menor valor
observado de la variable.
R = xmáx - xmín
El rango indica la variabilidad existente entre las
observaciones de un conjunto de datos, sin
embargo, debe usarse con precaución, ya que su
valor es función únicamente de dos valores
extremos pertenecientes al conjunto.

44. Varianza
Representa la variabilidad de una
serie de datos respecto a su media.
Puede sufrir un cambio muy
desproporcionado, aún más que
la media, por la existencia de
algunos valores extremos en el
conjunto de datos.
n si es población. (n-1) si es muestra

45. Desviación estandart
Es la raíz cuadrada de la varianza
La raíz cuadrada de la
varianza se denomina
desviación estándar o
desvío típico.

46. A menudo se prefiere la desviación estándar con
relación a la varianza, porque se expresa en las
mismas unidades físicas de las observaciones.
La desviación estándar nos permite determinar,
con un buen grado de precisión, dónde están
localizados los valores de una distribución de
frecuencias con relación a la media.

47. Coeficiente de variación
Muchas veces nos interesa comparar la variabilidad entre dos o más
conjuntos de datos.
Puede hacerse esto con sus respectivas varianzas o desviaciones
estándar cuando las variables se dan en las mismas unidades, y sus
medias son aproximadamente iguales.
Cuando no sucede esto, utilizamos una medida relativa de
variabilidad llamada coeficiente de variación.
El coeficiente de variación es el cociente entre la desviación
estándar y la media aritmética.

48. Esta medida es
independiente de
las unidades
utilizadas.
Se expresa en %

49. Retomemos el
ejemplo inicial de
las estaturas de los
estudiantes

56. El contenido multimedia es esencial en
una presentación, para dejar a todo el
mundo con la boca abierta. Además, así
sintetizarás el contenido y mantendrás a
tu audiencia entretenida.
Inserta un vídeo
Te damos la bienvenida a Genially
Te damos la bienvenida a Genially

57. Pregunta
interactiva Escribe una frase para que tu audiencia indique
si es verdadera o falsa.
Verdadero Falso
Send

58. ¡Recuerda publicar!