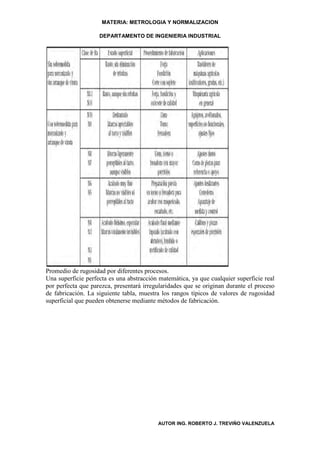
El documento habla sobre la metrología. Explica que la metrología estudia la medición de magnitudes como longitudes, masas, tiempos, etc. También describe cómo se usan símbolos y unidades de medida en la metrología para describir experimentos de una manera ordenada. Finalmente, menciona que los primeros sistemas de medición en la antigüedad se basaban en partes del cuerpo humano y permitieron establecer equivalencias para el intercambio de bienes entre comunidades.



























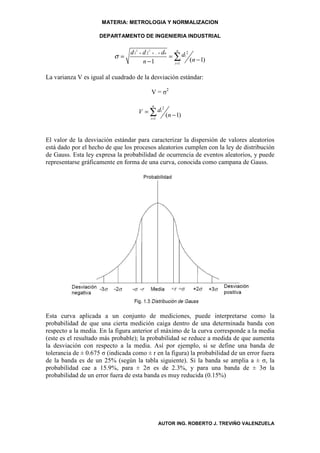























![MATERIA: METROLOGIA Y NORMALIZACION
DEPARTAMENTO DE INGENIERIA INDUSTRIAL
PRINCIPIO DEL MICRÓMETRO
El micrómetro es un dispositivo que mide el desplazamiento del husillo cuando éste es
movido mediante el giro de un tomillo, lo que convierte el movimiento giratorio del
tambor en el movimiento lineal del husillo; El desplazamiento de éste lo amplifica la
rotación del tomillo y el diámetro del tambor. Las graduaciones alrededor de la
circunferencia del tambor permiten leer un cambio pequeño en la posición del husillo.
En la figura suponga que el husillo es desplazado una distancia x desde los puntos a
hasta los b cuando el tomillo gira un ángulo α Denominando r al radio del tambor,
cualquier punto sobre la circunferencia se moverá la distancia dada por r. α [radio x
ángulo (en radianes) de giro]. Cuando el husillo es desplazado una distancia que es igual
al paso de los hilos del tomillo, p, las graduaciones sobre el tambor marcan una vuelta
completa. Estas relaciones pueden expresarse mediante las siguientes fórmulas.
Desplazamientolinealdelhusillo p x
= =
Desplazamientoangulardela sup erficiegraduada 2πr rα
Por lo tanto
pα
x=
2π
x = desplazamiento del husillo (mm)
p = paso de los hilos del tornillo (mm)
AUTOR ING. ROBERTO J. TREVIÑO VALENZUELA](https://image.slidesharecdn.com/metnor2comp-120821211531-phpapp02/85/Metnor2-comp-52-320.jpg)










![MATERIA: METROLOGIA Y NORMALIZACION
DEPARTAMENTO DE INGENIERIA INDUSTRIAL
Medidas de comparadores
Hay varios modelos, de distinto tamaño, forma y precisión de medidas. La elección
depende de la forma y espacio disponibles para realizar la medida o comparación.
1º. Forma. La esfera siempre es cilíndrica, pero varía la forma de sujeción al
soporte, que puede ser por la caña, o bien, por la tapa. La graduación normal de la esfera
es de cien divisiones, con un valor para cada una de ellas de una centésima; hay
comparadores de mayor precisión, cuyas divisiones son de una milésima o micra.
2º. Articulaciones. Para adaptarse a los lugares más o menos angostos, donde se
desea comparar, se acoplan articulaciones, más o menos ingeniosas, que solucionen el
problema.
3º. Palpadores. La punta de contacto, que realiza la comparación, dependerá de
la superficie que se desea verificar. En consecuencia, hay gran variedad de palpadores.
Normas para su empleo y conservación
Todos estos comparadores son aparatos delicados, por lo que hay que tratarlos con
sumo cuidado, si se desea que tengan larga vida en perfectas condiciones. Van
protegidos contra choques, en el eje principal, pero no así en el resto.
Bloques patrón
El calibrador de bloque, también conocido como “Bloques de Jo”, fue desarrollado por
el inventor sueco Carl Edward Johansson. Johansson fue empleado en 1888 como
inspector de armamento en una fabrica de fusiles en la ciudad de Eskilstuna, Suecia. La
necesidad de probar un nuevo diseño de arma, lo llevo a concebir la idea de construir un
conjunto de bloques rectangulares con medidas fijas que se pudieran combinar para
proporcionar una gran cantidad de longitudes. En mayo de 1901 Johansson recibió su
primera patente para el conjunto de bloques que construyo recibiendo el nombre en
inglés“Gauge Block Sets for Precision Measurement” cuya traducción
sería“Conjunto de bloques para medición exacta[1]” Hoy en día se conocen
comercialmente como bloques patrón.
Los bloques patrón son los dispositivos de longitud materializada más precisa[2] que
existe y es, además, donde inicia la diseminación[3] de la unidad de longitud hasta sus
últimas consecuencias (producto final).
Desde su invención hasta nuestros días, los bloques patrón han evolucionado en sus
características de diseño y construcción e inclusive deben cumplir con la norma
internacional ISO 3650. Los requerimientos de los Bloques Patrón de Longitud (BPL)
son:
1. Exactitud dimensional y geométrica (longitud, paralelismo y planitud).
2. Capacidad de adherencia con otros bloques patrón (acabado superficial).
3. Estabilidad dimensional a través del tiempo.
4. Resistencia al desgaste.
5. Coeficiente de expansión térmica cercano a los metales comunes.
6. Resistencia a la corrosión.
AUTOR ING. ROBERTO J. TREVIÑO VALENZUELA](https://image.slidesharecdn.com/metnor2comp-120821211531-phpapp02/85/Metnor2-comp-63-320.jpg)