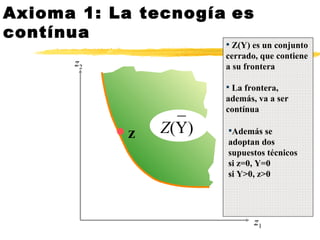
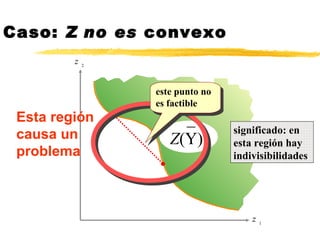
Este documento presenta los conceptos fundamentales de la producción, incluyendo la función de producción, eficiencia técnica, rendimientos a escala, isocuantas y producto marginal. Explica que la función de producción describe la relación entre los insumos y el producto, y que la eficiencia técnica ocurre cuando se produce la máxima cantidad posible. También define las isocuantas como la frontera de los insumos necesarios para producir un nivel dado de producto.

1. UNIVERSIDAD COMPLUTENSE DE MADRID D epartamento de Fundamentos del Análisis Económico I Microeconomía Superior II: Tema 1 Rafael Salas febrero de 2005

2. Esquema... Producción Optimización Mercados La empresa: Estática comparativa

3. Fundamentos de la producción... En este tema se establecen algunos elementos importantes para el análisis de las empresas . Lo hacemos en principio en un contexto de empresas productora de un solo producto... ...y (en principio) suponemos un contexto competitivo. Construimos el modelo ... Función de producción Eficiencia técnica Convexidad Sustituibilidad Rendimientos a escala Producto marginal

4. Notación Cantidades z i cantidad del input i z = (z 1 , z 2 , ..., z m ) vector de inputs cantidad de output Y Precios precio del input i w = (w 1 , w 2 , ..., w m ) vector de precios de Inputs precio del output P w i

5. La producción factible La relación básica entre output e inputs: Y  F ( z 1 , z 2 , ...., z m ) Esto puede expresarse más compactamente como: Y  F ( z ) Un único output, varios inputs La función de producción vector de inputs F proporciona la máxima cantidad de output que puede producirse dada una cantidad de inputs Distinguimos dos tipos de casos... Notad que usamos “  ” y no “=“ en la relación. Véamos el significado de F

6. Eficiencia técnica El caso donde la producción es ténicamente eficiente El caso donde producción es (técnicamente) ineficiente Caso 1: Y  F ( z ) Caso 2: Y  F ( z ) Intuición: si la combinación ( z ,Y ) es ineficiente, se podrían “tirar” varios inputs y seguir produciendo lo mismo

7. La función de producción z 2 Y z 1 0 output input 2 input 1 G ( z , z ) 1 2 Puntos no factibles Y > F ( z 1 ,z 2 ) Puntos tecnicam. eficientes Y = F ( z 1 ,z 2 ) Puntos factibles e ineficientes Y < F ( z 1 ,z 2 )

8. Esquema... Inputs necesarios Isocuantas Producción: Producto marginal

9. El conjunto de cantidades necesarias de inputs recordad, debemos tener Y  F ( z ) Selecciona un nivel de producto Y Buscad un vector factible z Repetid hasta encontrad todos los vectores de inputs El conjunto de cantidades necesarias de los inputs Z ( Y ) := { z: Y  F ( z )} El conjunto de vectores de inputs debe ser factible... La forma de Z depende de los supuestos sobre la tecnología... Primero, veamos el caso “standard” ...

10. El conjunto de cantidades necesarias de inputs: z 2 z 1 P. no factibles F ( z 1 ,z 2 ) <  Y Factibles, pero ineficientes F ( z 1 ,z 2 ) >  Y P. técnicamente eficientes F ( z 1 ,z 2 ) =  Y _ Z (Y)

11. Axioma 1: La tecnogía es contínua z Z(Y) es un conjunto cerrado, que contiene a su frontera La frontera, además, va a ser contínua Además se adoptan dos supuestos técnicos si z=0, Y=0 si Y>0, z>0 z 2 z 1 _ Z (Y)

12. Axioma 2: Z es monótono z Dado un z que pertenece a Z(Y) y dado un z  que no emplea menos cantidades que z Entonces z  pertenece también a Z(Y) z 2 z 1 z  Significado: existe eliminación gratuita (si aumentamos los inputs podemos producir lo mismo) _ Z (Y)

13. Axioma 3: Z es convexo z  z  z 2 z 1 Elige dos puntos Los puntos intermedios deben estar en Z (posiblemente en la frontera) significado: una combinación de técnicas factibles es factible Dibuja una linea recta entre ellos _ Z (Y)

14. Caso: Z no es convexo z 1 z 2 significado: en esta región hay indivisibilidades este punto no es factible _ Z (Y) Esta región causa un problema

15. Caso: Z e s convexo pero no suave z 1 z 2 El único punto eficiente F ( z 1 ,z 2 ) =  Y La pendiente no está definida en este punto _ Z (Y)

16. Esquema... Inputs necesarios Isocuantas Producción: Producto marginal

17. Isocuantas Seleccionad un nivel de Y Buscad el conjunto necesario de factores Z (Y) La isocuanta es la frontera de Z(Y) { z : F ( z ) = Y } Veamos la forma de la isocuanta  F( z ) F i ( z ) := ——  z i . F j ( z ) —— F i ( z ) Si la función F es diferenciable en z entonces la relación marginal de sustitución técnica es la pendiente en z : Usamos subíndices para denotar derivadas parciales. Así Nos dice la tasa de sustitución entre factores a lo largo de una isocuanta – que mantiene Yconstante

18. La isocuanta es la frontera de Z { z : F ( z ) = Y } z 1 z 2 Pend. = z 2 / z 1 isocuanta por A La relación de inputs describen la técnica productiva A inputs requiridos para producir A

19. La relación marginal de sustitución técnica (Y) La pendiente de la isocuanta es la relación marginal de sustitución en A. Nos indica el número de unidades necesarias de 2 para sustituir a una de 1, infinitesimalmente, y seguir produciendo lo mismo. z 1 z 2 A A' F 1 ( z )/F 2 ( z ) ratio de input

20. La elasticidad de sustitución (Y) z 1 z 2 A A' La respuesta del ratio de factores a la RMST es la elasticidad de sustitución  log( z 1 / z 2 )    log(F 1 /F 2 ) Puede entenderse como una medida de la “curvatura” de la isocuanta Un caso especial... F 1 ( z )/F 2 ( z ) ratio de inputs

21. Elasticidad de sustitución constante: Incremento de la elasticidad de sustitución... z 1 z 2 Veamos la estructura del mapa de isocuantas...

22. Isocuantas homotéticas z 1 z 2

23. Funciones homogéneas z 1 z 2 Y tz 1 tz 2 t r Y F ( t z ) = t F ( z ) r

24. Incremento proporcional de todos los inputs: RCE z 2 Q z 1 Rayo de expansión 0 F ( t z ) = t F ( z ) Rendimientos constantes a escala

25. Incremento proporcional de todos los inputs: RCreE z 2 Q z 1 0 t >1  F( t z ) > t F ( z ) Rendimientos crecientes a escala

26. Incremento proporcional de todos los inputs: RDE z 2 Q z 1 0 t >1  F ( t z ) < t F ( z ) Rendimientos decrecientes a escala

27. Tomemos una sección “horizontal” ...para obtener la noción de la isocuanta z 2 Q z 1 isocuanta Y =  Y 0

28. Práctica EJERCICIO: Dibuje las isocuantas correspondientes a: Y=  z 1 +  z 2 Y=min(z 1 /  , z 2 /  ) Y= z 1  z 2  Y=  z 1 2 +  z 2 2 donde  y  0 Indique los rendimientos a escala y el valor de la elasticidad de sustitución .

29. Práctica EJERCICIO: Calcule la elasticidad de sustitución correspondiente a: Y= {   z 1  +   z 2  } 1/  donde  i  0   y 1   Indique los rendimientos a escala .

30. Tomemos ahora una sección “vertical”... z 2 Q z 1 0 … esto nos proporciona nuestro nuevo concepto

31. Esquema... Inputs necesarios Isocuantas Producción: Producto marginal

32. Producto marginal Medimos el cambio marginal en el output con respecto a ese input  F( z ) ——  z i Pmgi = F i (z) = Seleccione un vector de inputs técnicamente eficiente Varíe un input y deje los demás costantes Recuerde, esto significa que elegimos z tal que Y = F ( z ) Veamos su forma El producto marginal

33. Posibles relaciones entre el output y un input Tomemos el caso convencional… z 1 Q F ( z ) z 1 Y F ( z ) z 1 Y F ( z ) z 1 Q F ( z )

34. Veamos la relación entre el output y el input 1... F ( z ) Y z 1 Conjunto de técnicas eficientes Input 1 es esencial: Si z 1 =0, Y=0 Conjunto factible

35. Producto marginal z 1 Y F ( z ) F 1 cae con z 1 si F es cóncava pendiente = F 1 ( z )

36. UNIVERSIDAD COMPLUTENSE DE MADRID D epartamento de Fundamentos del Análisis Económico I Microeconomía Superior II: Tema 1 Rafael Salas febrero de 2005