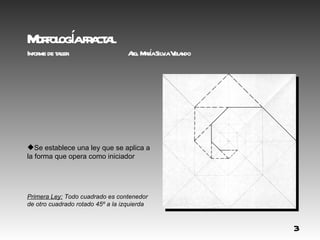
El documento describe cómo se construyen las formas fractales a partir de iniciadores y la aplicación repetida de leyes simples. Explica que cualquier objeto puede ser un iniciador y que las primeras exploraciones se hicieron en el plano. Luego, usando un cuadrado plegado como iniciador, se establecen dos leyes que involucran rotaciones y yuxtaposiciones de figuras para generar formas cada vez más complejas de manera iterativa.

1. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a

2. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
La construcción de formas fractales
se origina a partir de iniciadores.
Cualquier forma u objeto puede
constituírse en inciador.
Las primeras exploraciones fueron realizadas
a partir del dibujo sobre el plano
1

3. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
En una segunda exploración se trabaja con
formas que se desarrollan en tres
dimensiones, determinandose como iniciador
un cuadrado al cual se le realiza un pliegue
del triángulo superior derecho.
2

4. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
Se establece una ley que se aplica a
la forma que opera como iniciador
Primera Ley: Todo cuadrado es contenedor
de otro cuadrado rotado 45º a la izquierda
3

5. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
Iteración: Una de las características
de las formas fractales es la de
generarse a partir de la repetición
infinita de un mismo proceso, que
puede ser “bloqueado” tanto por
limitaciones materiales o por decisiones
de diseño
4

6. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
La posibilidad de aplicar sucesivas
leyes a la forma posibilita cierto control
de la resultante, que no anula la
componente de impredictibilidad propia
de ésta geometría.
Segunda ley: Al pliegue triangular se le
yuxtapone perpendicularmente un cuadrado.
5

7. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
En la geometría fractal el uso de
leyes simples puede producir formas de
alto grado de complejidad.
Se repite la operación en cada triángulo y
comienza a constituirse una forma compleja
a partir de formas simples.
6

8. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
Autosemejanza: la forma se repite a
sí misma a escalas cada vez más
pequeñas contenedoras de infinitas
copias de si mismas
7

9. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
Resultante obtenida a partir del generador
8

10. M fol í fr ct l
or oga a a
Infor de t ler
me al r aí v el ndo
Aq. M raSil iaV a
Resultante obtenida a partir del generador
9