Movimiento Ondulatorio

ANDALUCÍA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
www.profes.net es un servicio gratuito de Ediciones SM
OPCIÓN A
2. Considere la siguiente ecuación de una onda :
y ( x , t ) = A sen ( b t - c x ) ;
a) ¿qué representan los coeficientes A, b, c ? ; ¿cuáles son sus unidades? ;
b) ¿qué interpretación tendría que la función fuera “coseno” en lugar de “seno” ?; ¿y
que el signo dentro del paréntesis fuera + en lugar de - ?
a) Comparando la expresión dada con la ecuación general de una onda encontramos que:
( ) ( )kxtωsen·At,xy −=
A es la amplitud de la onda que indica el valor máximo de la elongación que sufren los
puntos del medio por los que pasa la onda. Sus unidades en el S.I. son los metros.
b es la pulsación o frecuencia angular, ⎟
⎠
⎞
⎜
⎝
⎛
== fπ2
T
π2
ω , sus unidades en el sistema
angular son rad/s.
c es el número de ondas
λ
π2
k = , indica el número de longitudes de onda que hay en la
distancia 2π. Sus unidades son rad/m.
b) Tanto la función seno como la función coseno son útiles para definir el movimiento
periódico de una partícula en el espacio o en el tiempo ya que ambas varían de igual modo
y toman sus valores entre –1 y +1. La única diferencia entre ambas es que se encuentran
desfasadas 90º.
El signo del interior del paréntesis indica el sentido de desplazamiento de la onda. Cuando
el signo es positivo la onda se desplaza en el sentido negativo del eje de abscisas y cuando
el signo es negativo, la onda se desplaza en el sentido positivo.

ANDALUCÍA / SEPTIEMBRE 04. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
OPCIÓN A
1. Considere la onda de ecuación :
y (x , t ) = A cos ( b x ) sen ( c t ) ;
a) ¿Qué representan los coeficientes A, b, c ? ; ¿cuáles son sus unidades? ; ¿cuál es el
significado del factor A cos ( b x ) ?
b) ¿Qué son los vientres y los nodos? ; ¿qué distancia hay entre vientres y nodos
consecutivos?
a) La ecuación dada es la que corresponde a la ecuación del movimiento para una onda
estacionaria. Se obtiene superponiendo dos ondas que se propagan con la misma
frecuencia, amplitud y dirección pero en distinto sentido.
( ) ( )
( ) ( )kxtωsen'Akxtωsen'Ayyy
kxtωsen'Ay;kxtωsen'Ay
21
21
−++=+=
−=+=
La suma de dos senos se puede expresar como:
2
ba
sen·
2
ba
os2bsenasen
+−
=+
sustituyendo kxtωbykxtωa −=+= , tenemos
tωsen·kxcos'A2
2
kxtωkxtω
sen·
2
kxtωkxtω
cos'A2y =
−+++−+
=
Comparando este resultado con las ecuaciones de las ondas que interfirieron inicialmente
podemos concluir que:
A = 2A' Es el doble de la amplitud de las ondas incidentes. Se mide en metros
B = k Es el número de onda que india el número de longitudes de onda que hay en la
distancia 2π. Se mide en m-1
.
C = ω Es la pulsación o frecuencia angular de las ondas incidentes. Se mide en
Hercios Hz = s-1
..
El factor A·cos(bx) indica la amplitud con la que vibran cada uno de los puntos de la onda
estacionaria que como se puede comprobar depende de la posición..
b) Los vientres son los puntos de la onda en los
que se vibra con la máxima amplitud. La
distancia entre dos vientres consecutivos es
media longitud de onda.
Los nodos son los puntos donde no se produce
vibración. La distancia entre dos nodos
consecutivos también es media longitud de onda.
La distancia entre un vientre y un nodo es un
cuarto de longitud de onda.
vientre
nodos
La línea punteada marca la máxima
vibración de cada punto de la onda
La línea roja muestra un momento
cualquiera de la vibración

ANDALUCÍA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 3
3. Una partícula de 0,5 kg que describe un movimiento armónico simple de frecuencia
5/ Hz tiene, inicialmente, una energía cinética de 0,2 J y una energía potencial de 0,8
J.
a) Calcula la posición y la velocidad iniciales, así como la amplitud de la oscilación y la
velocidad máxima.
b) Haz un análisis de las transformaciones de energía que tienen lugar en un ciclo
completo. ¿Cuál será el desplazamiento en el instante en que las energías cinética y
potencial son iguales?
La ecuación de la posición de una partícula con un movimiento armónico simple es:
x = A · sen(ω · t + φ) = A · sen(2 · π · f · t + φ)
Por tanto la velocidad es:
dt
dx
= 2 · π · f · A · cos(2 · π · f · t + φ)
Si sustituimos los valores en las dos expresiones tenemos que:
x = A · sen (10 · t + φ)
v = A · 10 · cos (10 · t + φ)
La energía potencial se representa como: · xk·
2
1
E 2
p =
La energía cinética se representa como: 2
C · vm·
2
1
E =
En un movimiento oscilatorio armónico simple la energía potencial máxima es igual a la energía
cinética máxima, de manera que:
2
max
2
max · vm·
2
1
· xk·
2
1
=
Es decir, k · A2
= m · ω2
· A2
Por tanto; k = m · ω2
= 0,5 · (2 · π · 5 · π-1
)2
= 50 N · m-1
Para t = 0, tenemos:
Ep =
2
1
· 50 · x0
2
= 0,8 J ; x0 = 0,18 m
Ec =
2
1
· 0,5 · v0
2
= 0,2 J; v0 = 0,89 m · s-1
La velocidad máxima vendrá definida por la energía cinética máxima, que tiene lugar cuando la
potencial es cero y su valor es el de la suma de la energía potencial y cinética del instante
inicial:
Etotal = ECmax =
2
1
· 0,5 · vmax
2
= 0,8 + 0,2 = 1 J ; vmax = 2 m · s-1
La distancia máxima vendrá definida por la energía potencial máxima, que tiene lugar cuando la
cinética es cero:

Etotal = EPmax =
2
1
· 50 · xmax
2
= 1 J ; xmax = 0,2 m
b) En un ciclo la velocidad y la energía cinética máximas tienen lugar cuando la energía potencial
es nula, es decir x = 0. De igual manera la energía potencial máxima tiene lugar cuando el
desplazamiento es máximo y la velocidad es nula.
Si ambas energía son iguales, la energía potencial será la mitad de la máxima:
Ep =
2
1
· 50 · x2
=
2
1
· 1 J
Por tanto: x = 0,14 m

ANDALUCÍA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 3
3. Se hace vibrar el extremo de una cuerda con una amplitud de 5 cm y una frecuencia
de 50 Hz. La velocidad de propagación de la onda es de 1 000 m · s-1
.
a) Escribe la ecuación de este movimiento ondulatorio sabiendo que la elongación del
punto x = 0 en el instante t = 0 es nula.
b) Representa la elongación de todos los puntos de la cuerda en el instante t = 1 s.
a) La ecuación general del movimiento de una onda es:






φ+
λ
π
νπ=φ+ω= x
·2
-· t··2sen·A)· xk-· t(sen·At)(x,y
La velocidad de la onda es: f·
T
v λ=
λ
= , por tanto, m20
50
0001
f
v
===λ
Sustituyendo los datos obtenemos la ecuación: 





φ+
π
π= x
20
·2
-· t50··2sen·0,05t)(x,y
Si sustituimos para t = 0, x = 0 obtenemos que: sen φ = 0, y por tanto, φ = 0.
Finalmente la ecuación queda: ( )x··0,1-· t·100sen·0,05t)(x,y ππ=
b) Para el instante t = 1 s, la ecuación es:
( ) ( )x··0,1sen·50,0x··0,1-·100sen·0,051)(x,y π−=ππ=
Su representación gráfica es:

ANDALUCÍA / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN A / CUESTIÓN 2
OPCIÓN A
2. a) Explique las diferencias entre ondas transversales y ondas longitudinales y ponga
algún ejemplo.
b) ¿Qué es una onda estacionaria? Comente sus características.
a) Las ondas transversales y longitudinales son las que se clasifican atendiendo a su
dirección de propagación.
Las longitudinales son aquellas en las que la dirección de propagación coincide con la
dirección de vibración. Son ondas longitudinales las del sonido o las que se propagan en un
muelle cuando vibra longitudinalmente.
Las transversales son aquellas en las que la dirección de propagación es perpendicular a la
dirección en que tiene lugar la vibración. Son ondas transversales las ondas
electromagnéticas y las ondas sísmicas s.
b) Una onda estacionaria se forma cuando interfieren dos ondas de características iguales,
que se propagan en la misma dirección, pero en sentidos diferentes. El fenómeno se debe a
que en la superficie de separación de dos medios se produce una reflexión como ocurre por
ejemplo en las ondas que produce la cuerda de una guitarra. Estas ondas se denominan
estacionarias porque dan lugar a un patrón de vibración estacionario.
El patrón de vibración depende de que los límites sean fijos o libres, de forma que se
pueden obtener distintas frecuencias fundamentales y diferentes armónicos que son los
múltiplos de la frecuencia fundamental obtenida en cada caso. Las zonas donde la vibración
es máxima se denominan vientres y las de vibración nula, nodos.
Una onda estacionaria, en realidad, no representa un movimiento ondulatorio ya que no hay
transporte neto de energía de unos puntos a otros. Cada uno de los puntos de l medio,
excepto los nodos vibra como si se tratase de un oscilador armónico con una amplitud de
terminada de modo que el perfil de la onda no se desplaza. Entre dos nodos la energía
permanece estancada.

ANDALUCÍA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
4. Una onda plana viene dada por la ecuación: y(x, t) = 2 · cos (100 · t - 5 · x) (S.I.)
donde x e y son coordenadas cartesianas.
a) Haga el análisis razonado del movimiento ondulatorio representado por la ecuación
anterior y explique si es longitudinal o transversal y cuál es su sentido de propagación.
b) Calcule la frecuencia, el período, la longitud de onda y el número de onda, así como
el módulo, dirección y sentido de la velocidad de propagación de la onda.
a) La onda del enunciado se propaga en el eje de las x puesto que la fase de la onda depende del
tiempo y de la posición x. Se propaga en el sentido de las x positivas, ya que el término del
espacio y el del tiempo tienen signos cambiados. Esto se puede ver ya que para que la fase se
mantenga constante cuando aumenta el tiempo, el punto x debe también aumentar.
Finalmente, puesto que la onda se representa en un eje perpendicular a la trayectoria se trata
de una onda transversal.
b) La ecuación general de una onda es: y(x, t) = A · cos (ω · t - k · x), donde ω es la frecuencia
angular y k es el número de onda. Por tanto tenemos los siguientes datos:
ω = 100 rad · s-1
; k = 5 m-1
Puesto que: νπ=ω ··2 tenemos que la frecuencia vale: Hz9,15
·2
100
·2
=
π
=
π
ω
=ν
Por tanto el periodo de la onda es: s063,0
9,15
11
T ==
ν
=
La longitud de onda se determina a partir del número de onda: m26,1
5
·2
k
·2
=
π
=
π
=λ
Por último la velocidad de propagación es: 1-
s·m20
063,0
26,1
T
v ==
λ
=
Por tanto la velocidad, como vector es: -1
s·mi20v
rr
=

ARAGÓN / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN A / EJERCICIO 1
EJERCICIO 1
1) Un muelle de masa despreciable tiene una longitud natural
L0 = 20 cm. Cuando de su extremo inferior se cuelga un cuerpo de
masa M = 0,1 kg, la longitud en equilibrio del muelle es Leq = 30 cm.
a) Calcula la constante recuperadora, k, de este muelle. Considera
g = 10 m/s2
. (0,5 p.)
Partiendo de la posición de equilibrio anterior, se desplaza M hacia
arriba 10 cm, es decir, hasta que el muelle tiene su longitud natural. A
continuación se suelta M con velocidad inicial nula, de forma que
empieza a oscilar armónicamente en dirección vertical.
b) Calcula la longitud máxima del muelle, en el punto más bajo de la oscilación de M. (1 p.)
c) Calcula la amplitud y la frecuencia de la oscilación, y la velocidad de M cuando pasa por su
posición de equilibrio. (1 p.)
a) La fuerza recuperadora del muelle se equilibra con la fuerza del peso del cuerpo.
m/N10
1,0
10·1,0
x∆
mg
k;g·mx∆·kPFk ====⇒=
b) La amplitud de la oscilación es igual a uno y otro lado de la posición de equilibrio del muelle, por
tanto el punto más bajo de la oscilación se encuentra 10 cm por debajo de la posición de equilibrio:
m4,0cm40Lmax ==
c) La amplitud de la oscilación es un dato del apartado b) (A = 10 cm)
La frecuencia se puede obtener a partir del valor de k:
s/rad10
10
1,0
m
k
ωωmk 2
===⇒=
Para el calculo de la velocidad utilizamos la ecuación del m.v.a.s.:
t10sent10sen10·1,0vtωsenωAvtωcosAy −=−=−=⇒=
Calculamos el valor de t cuando pasa por la posición de equilibrio, es decir cuando y = 0
s
20
π
tπn2
2
π
t10;0t10cos;t10cos100 =⇒+===
sustituyendo en la ecuación de la velocidad
s/m1
2
π
sen
20
π
·10senv −=−=⎟
⎠
⎞
⎜
⎝
⎛
−=
El valor máximo de la velocidad en módulo es 1m/s y se obtiene cuando el cuerpo pasa por la posición
de equilibrio.

ARAGÓN / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN B / ACTIVIDAD 1
OPCIÓN B
1) a) ¿Qué es una onda estacionaria? Explica qué condiciones deben cumplirse para
que se forme una onda estacionaria en una cuerda tensa y fija por sus dos
extremos. (1,5 p.)
b) Una cuerda de guitarra de longitud L = 65 cm vibra estacionariamente en su
modo fundamental a una frecuencia f = 440 Hz. Representa gráficamente el perfil
de esta onda, indicando la posición de nodos y vientres, y calcula la velocidad de
propagación de ondas transversales en esta cuerda. (1 p.)
RESPUESTA
a) Una onda estacionaria es el resultado de la interferencia de dos ondas de iguales
características, que se propagan en la misma dirección pero en sentidos contrarios. Se
denominan estacionarias porque producen un patrón de vibración estacionario.
Para que se produzca una onda estacionaria, uno de los extremos de la onda no debe vibrar
(nodo) y el otro puede estar fijo o libre (nodo o vientre). En el caso de la cuerda definida, los
dos extremos están fijos y por tanto son nodos.
b) λ = 2L = 130 cm
s/m572440·3,1fλ
T
λ
vp ====
nodos
vientre

ARAGÓN / SEPTIEMBRE 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN B
1) a) Escribe la ecuación de una onda armónica y comenta el significado físico de
las magnitudes que aparecen en dicha ecuación. (1,5 p.)
Una onda armónica transversal se propaga en el sentido positivo del eje OX con
velocidad v = 50 m/s. La amplitud de la onda es A = 0,15 m y su frecuencia es f =
100 Hz. La elongación del punto situado en x = 0 es nula en el instante t = 0.
b) Calcula la longitud de onda. (0,5 p.)
c) Calcula la elongación y la velocidad transversal del punto situado en x = 5 m,
en el instante t = 0,1 s. (1 p.)
RESPUESTA
a) La ecuación general de una onda armónica es:
b)
( )KxtωAsen)t,x(y ±=
Donde:
• A es la amplitud del movimiento ondulatorio y se mide en metros.
• ω es la frecuencia angular;
T
π2
fπ2ω == se mide en rad/s
• t es el tiempo que transcurre desde que se inició el movimiento ondulatorio y se mide
en segundos
• ± Indican el sentido en el que se desplaza la onda. El signo negativo indica que se
desplazan en el sentido de avance del eje X y el positivo lo contrario.
• K se denomina número de ondas, es el número completo de longitudes de onda que
caben en π2 metros;
λ
π2
k = se mide en rad/m
• x es la distancia en metros al punto donde se genera la onda.
b) m5,0
100
50
f
v
λfλv ===⇒=
c) Escribimos la ecuación de la onda:
( )xπ4tπ200sen15,0)t,x(y −=

ARAGÓN / SEPTIEMBRE 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
La ecuación de la velocidad de vibración es:
( )xπ4tπ200sen15,0π200)t,x(v −=
Sustituimos para los valores dados
( ) m0π20π20sen15,0)1,0;5(y =−=
( ) s/mπ30π20π20sen15,0π200)1,0;5(v =−=

ZARAGOZA / JUNIO 2000. LOGSE / FÍSICA / OPCIÓN A / CUESTIÓN 1 /
VIBRACIONES Y ONDAS
1. La bolita de un péndulo simple realiza una oscilación aproximadamente horizontal y
armónica, en presencia del campo gravitatorio terrestre, con un periodo T = 2 s y una
amplitud A = 2 cm.
a) Obtén la ecuación de la velocidad de la bolita en función del tiempo, y represéntala
gráficamente. Toma origen de tiempo (t = 0) en el centro de la oscilación. (1 p.)
b) ¿Cuál sería el periodo de oscilación de este péndulo en la superficie de la Luna, donde
la intensidad del campo gravitatorio es la sexta parte del terrestre? (1 p.)
a) La frecuencia angular es: π=
π
=
π
=ω
2
2
T
2
La oscilación será: x = 0,02 sen(π t) (m)
b) El periodo de oscilación de un péndulo es: T = 2 π
g
L
Si se varía la gravedad se tendría: T’ = 2 π s4,92·6T6
6/g
L
===

ARAGÓN / JUNIO 01. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
Considera dos tubos de la misma longitud, L = 0,68 m, el primero con sus dos extremos
abiertos a la atmósfera y el segundo con uno abierto y otro cerrado.
a) Calcula, para cada tubo, la menor frecuencia de excitación sonora para la que se
formarán ondas estacionarias en su interior. Calcula la longitud de onda correspondiente
en cada caso.
b) Representa la onda estacionaria que se forma dentro de cada tubo, indicando la
posición de nodos y vientres.
La velocidad de propagación del sonido en el aire es v = 340 m/s.
a) Las ondas sonoras estacionarias tienen mínimos en las zonas cerradas de las cavidades y
máximos en sus extremos abiertos. Un tubo con los dos extremos abiertos tiene por tanto un
máximo en cada extremo, pudiendo tener tan sólo media onda estacionaria. Por tanto la longitud
de onda será: λ = 2 L = 2 · 0,68 = 1,36 m.
Su frecuencia será: Hz250
36,1
340
===
λ
v
f
Si el tubo tiene un extremo cerrado y otro abierto puede tener tan sólo un cuarto de onda, por
tanto: λ = 4 L = 4 · 0,68 = 2,72 m.
Su frecuencia será: Hz125
72,2
340
===
λ
v
f
b) La representación gráfica es la siguiente:
Vientre
Nodo
Vientres
Nodo

ARAGÓN / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A /
PREGUNTA 1
www.profes.netes un servicio gratuito de Ediciones SM
OPCIÓN A
1. Una cuerda tensa, fija por sus dos extremos, tiene una longitud L = 1,2 m. Cuando
esta cuerda se excita transversalmente a una frecuencia n = 80 Hz, se forma una onda
estacionaria con dos vientres.
a) Calcula la longitud de onda y la velocidad de propagación de las ondas en esta cuerda.
(1,5 puntos)
b) ¿Para qué frecuencia inferior a la dada se formará otra onda estacionaria en la
cuerda? Representa esta onda. (1 punto)
a) Si se forma una onda estacionaria con dos vientres (2º
armónico), como se puede observar en la imagen, lo que
tenemos entre los dos extremos fijos es una longitud de
onda, por lo tanto:
m2,1L ==λ
s/m9680·2,1f·vp
==λ=
b) Se forma otra onda estacionaria cuando entre los
extremos fijos solo hay un vientre (1er
armónico). En este
caso a longitud de onda es:
m4,2L2 ==λ
Hz40
4,2
96
L2
v
f
p
===

ARAGÓN / JUNIO 03. SELECTIVIDAD / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN B / PREGUNTA 4
OPCIÓN B
4) Por una cuerda tensa situada a lo largo del eje OX se propaga, en el sentido positivo
de dicho eje, una onda transversal armónica. En la figura 1 se muestra el perfil de la
onda en t = 0, y en la figura 2 se representa, en función del tiempo, el desplazamiento
transversal del punto de la cuerda situado en x = 0.
a) Determina las siguientes magnitudes de la onda: amplitud, longitud de onda y
velocidad de propagación. (1,5 p.)
b) Escribe la ecuación de la onda, y (x, t). (1 p.)
a) La amplitud del movimiento se puede medir tanto en la figura 1 como en la 2, es A = 2 mm.
La longitud de onda se mide en el eje x de la figura 1, λ = 2 m
Para conocer la velocidad de propagación hay que encontrar en primer lugar el valor del periodo.
En la segunda gráfica observamos que un punto tarda 10 ms en volver a estar en el mismo estado
de vibración luego T = 10 ms. Ahora calculamos el valor de la velocidad de propagación:
s/m200
01,0
2
T
vp
==
λ
=
b) La ecuación de la onda es:
( ) 





λ
π
±
π
=±ω= x
2
t
T
2
·cosAkxt·cosA)t,x(y
Los valores de k y ω son: s/rad200
01,0
2
T
2
;m/rad
2
22
k π=
π
=
π
=ωπ=
π
=
λ
π
=
Como se dirige en la dirección positiva del eje OX, en la ecuación se utiliza el signo negativo.
Para que en t = 0 y x = 0 el valor de y = 0 tiene que haber un desfase de π/2.
Con todos estos datos ya podemos escribir la ecuación de la onda:
( ) 




 π
+π−π=ϕ+±ω= −
2
xt200cos10·2kxt·cosA)t,x(y 3
0

ZARAGOZA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 1
1. Un péndulo simple está construido con una bolita suspendida de un hilo de longitud
L = 2 m. Para pequeñas oscilaciones, su periodo de oscilación en un cierto lugar resulta
ser T = 2,84 s.
a) Determina la intensidad del campo gravitatorio en el lugar donde se ha medido el
periodo. (1 punto.)
b) Considera que el movimiento de la bolita es prácticamente paralelo al suelo, a lo
largo de un eje OX con origen, O, en el centro de la oscilación. Sabiendo que la
velocidad de la bolita cuando pasa por O es de 0,4 m/s, calcula la amplitud de su
oscilación y representa gráficamente su posición en función del tiempo, x(t). Toma
origen para el tiempo, t = 0, en un extremo de la oscilación. (1,5 puntos.)
a) El periodo de un péndulo simple viene dado por la siguiente ecuación:
g
l
··2T π=
Despejando la aceleración de la gravedad y sustituyendo los valores se obtiene su valor:
s·m9,792,842
2,84
2··4
T
l··4
g 2-
2
2
2
2
=
π
=
π
=
b) La forma funcional de la oscilación es: x = A · sen(ω · t + φ)
En este caso la velocidad, obtenida derivando la posición, será: v = A · ω · cos(ω · t + φ)
En el punto de menor amplitud tenemos que: sen(ω · t + φ) = 0; ω · t + φ = 0
Por tanto la velocidad en ese instante es: v = A · ω
Despejando y sustituyendo los valores se obtiene la amplitud de la oscilación:
1-s·rad0,18
·2
2,84·0,4
·2
T·v
T
·2
vv
A =
π
=
π
=
π
=
ω
=
La ecuación del movimiento en grados es:





 π
+=




 π
+
π
=
2
· t2,21sen·0,18
2
· t
T
·2
sen·0,18x
Donde se ha introducido el desfase
2
π
de para que a tiempo cero la posición sea un extremo de
la oscilación.
La gráfica del movimiento es:

ZARAGOZA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
4. Una onda transversal armónica se propaga a lo largo del eje OX, en sentido positivo.
Su amplitud es 10-3
m; su frecuencia, 30 Hz, y su longitud de onda, 4 m. En el instante
t = 0, el desplazamiento transversal en x = 0 es y0 = -10-3
m.
a) Escribe la ecuación de la onda. ¿Cuál es su velocidad de propagación? (1 punto.)
b) Calcula la diferencia de fase entre las oscilaciones de dos puntos separados 2 m. (1
punto.)
a ) La ecuación general de una onda que se mueve en el sentido positivo del eje X es:
y (x, t) = A · sen(k · x - ω · t + φ) = 





φ+π
λ
π
· tf··2-
· x·2
sen·A
Por tanto, si sustituimos A = 10-3
m, λ = 4 m, y f = 30 Hz obtenemos la ecuación:






φ+π
π
=





φ+π
π
= · t·60-
2
· x
sen·0,001· t30··2-
4
· x·2
sen·0,001t)y(x,
Para determinar la fase hay que tener en cuenta que y (0, 0) = -0,001 = 0,001 · sen φ.
Por tanto: φ = -π/2.
La ecuación final es: 




 π
−π
π
=
2
· t·60-
2
· x
sen·0,001t)y(x, (m)
La velocidad se obtiene como: s·m12030·4f·
T
v 1-
==λ=
λ
=
b) Puesto que la separación de 2 m entre los dos puntos es
2
λ
, la diferencia de fase entre ellos
será de π radianes, o 180º.

ARAGÓN / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A /
Nº 1
Una partícula de masa m = 10 g oscila armónicamente en torno al origen de un eje OX,
con una frecuencia de 5 Hz y una amplitud de 5 cm.
a) Calcula la velocidad de la partícula cuando pasa por el origen.
b) Determina y representa gráficamente la energía cinética de m en función del tiempo.
Toma origen de tiempo, t = 0, cuando m pasa por x = 0.
a) El movimiento de la partícula es: A = A0 · sen(ω · t)
Por tanto la velocidad será: v = A0 · ω · cos(ω · t)
Sustituyendo se tiene una velocidad en el origen de:
v = A0 · ω = A0 · 2 · π · ν = 0,05 · 2 · π · 5 = 1,57 m · s-1
b) La energía cinética en función del tiempo es:
Ek =
2
1
· m · v2
=
2
1
· m · (A0 · ω · cos(ω · t))2
Sustituyendo:
Ek =
2
1
· 0,01 · 0,052
· (2 · π · 5)2
· cos2
(2 · π · 5 · t) = 1,23 · 10-2
· cos2
(31,4 · t) J
La gráfica es:
0 5 10 15 20
0.0
2.0x10
-3
4.0x10-3
6.0x10
-3
8.0x10-3
1.0x10
-2
1.2x10
-2
1.4x10
-2
Tiempo (s)
Energíacinética(J)

ARAGÓN / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A / Nº 4
a) Propagación de ondas en una dimensión; la ecuación de onda.
b) Una cuerda se tensa horizontalmente a lo largo de su eje OX, con origen O en su
extremo izquierdo. Este extremo se hace vibrar transversal y armónicamente con una
amplitud de 5 cm y una frecuencia de 10 Hz, de forma que por la cuerda se propaga una
onda con una velocidad de 20 m/s. Supuesto que en t = 0 la elongación del punto en x = 0
es máxima, escribe la ecuación de la onda. ¿Cuál es la velocidad máxima de movimiento
de un punto cualquiera de la cuerda?
a) Una onda unidimensional es un movimiento que se propaga en una única dimensión. La
ecuación que representa esto es: A = Amax · cos (2 · π · ν · t -
λ
π·2
· x + φ ).
La consideración de unidimensional afecta a la dirección de propagación y no a la de los puntos
materiales que conforman la onda. Su movimiento puede ser en la dirección de propagación o
transversalmente.
b) La ecuación de la onda es: A = Amax · cos (2 · π · ν · t -
λ
π·2
· x + φ ).
Si en x = 0, t = 0 la amplitud es máxima, se tiene que cos φ = 1, por tanto φ = 0.
La amplitud es: Amax = 5 cm.
La frecuencia ν = 10 Hz.
La longitud de onda es λ = m2
10
20v
==
ν
Sustituyendo los datos en la ecuación se tiene la ecuación de la onda:
A = 0,05 · cos (2 · π · 10 · t -
2
·2 π
· x ) = 0,05 · cos (20 · π · t - π · x ) (m)
La velocidad de un punto cualquiera es la derivada de la ecuación de ondas:
v = A’ = -0,05 · 20 · π · sen (20 · π · t - π · x ) = -π · sen (20 · π · t - π · x )
La velocidad máxima es el factor que multiplica al seno: vmax = π = 3,14 m · s-1

ZARAGOZA / SEPTIEMBRE 2000. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN A / CUESTIÓN 1
1. a) Enuncia el Principio de Huygens y, a partir de él, demuestra las leyes de reflexión y
refracción para una onda que incide sobre la superficie plana de separación entro des
medios, en los que la onda se propaga con velocidades diferentes v1 y v2. (1 p)
b) Una onda de frecuencia ν = 4 Hz se propaga por un medio con velocidad v1 = 2 m/s e
incide sobre la frontera con otro medio diferente con ángulo de incidencia ε = 30º. En el
segundo medio la velocidad de propagación de la onda es v2 = 2,5 m/s. Calcula el ángulo
de refracción y la longitud de onda en este segundo medio. (1 p.)
a) El principio de Huygens se basa en que la propagación de una onda se puede describir como la
superposición de una serie de ondas secundarias que se forman el frente de ondas de una onda
principal.
Esta sencilla descripción permite explicar fenómenos como los de reflexión o refracción de una
onda. En la reflexión la velocidad de la onda incidente y de la reflejada son iguales, por tanto sus
ángulos también lo serán. En la refracción la onda transmitida viaja a distinta velocidad, lo que
hace que el frente de onda se reconstruya con una dirección de propagación diferente a la que
tenía inicialmente.
b) La ley de refracción es: vt sen αt = vi sen αi
Despejando tenemos que: º6,230,430ºsen
5,2
2
sensen
v
v
sen tti
t
i
t =α⇒==α⇒α=α
Cuando una onda pasa de un medio a otro en el que se mueve con diferente velocidad la
frecuencia de la onda se mantiene, mientras que la longitud de onda varía.
Para las ondas, la longitud de onda se define como: λ = v T = v ν-1
=2,5 · 4-1
= 0,625 m

ZARAGOZA / SEPTIEMBRE 2000. SELECTIVIDAD / FÍSICA / VIBRAC. Y
4. Por una cuerda tensa se propaga una onda armónica dada por:
y(x, t) = A sen(2π (t/T-x/λ)
a) Explica el significado físico de cada una de las magnitudes que aparecen en esta
expresión. (1 p.)
b) Si λ = 0,5 m y T = 5 ms, calcula la velocidad de propagación de la onda. (0,5 p.)
c) Para A = 5 mm, calcula la velocidad de movimiento del punto de la cuerda situado en x
= 0,25 m en el instante t = 2,5 ms. (1 p.)
a) A es la amplitud de la onda que se propaga; T es el periodo de la onda, el tiempo que tarda la
onda en recorrer una longitud de onda; λ es la longitud de la onda, la separación entre dos puntos
con igual oscilación.
b) La velocidad de propagación de una onda es: m/s100
10·5
5,0
T
v 3
==
λ
= −
c) La velocidad transversal de un punto es la derivada temporal de la posición:
v(x, t) =
T
2π
A cos 











λ
−π
x
T
t
2 = 3-
10·5
2π
5 · 10-3
cos 











−π
5,0
25,0
10·5
10·5,2
2 3-
-3
= 6,28 m/s

ARAGÓN / SEPTIEMBRE 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN A
Cuestión 1
Una pequeña fuente sonora emite en el espacio con una potencia de 10 W,
uniformemente distribuida en todas las direcciones (onda esférica).
a) Calcula la intensidad del sonido a 10 m de dicha fuente, en unidades del S.I. (1 p.)
b) La intensidad de un sonido también puede medirse en decibelios (dB). Explica en qué
consiste la escala decibélica de medida de intensidad acústica. (1 p.)
c) ¿Cuál es la intensidad acústica, en dB, producida por nuestra fuente a 10 m de
distancia? (0,5 p.)
La intensidad umbral del oído humano es Io = 10-12
W/m2.
a) La intensidad sonora viene dada por la fórmula: 2
r4
P
I
⋅π⋅
=
Sustituyendo los datos del enunciado: 23
mW107,95 −−
⋅⋅=
⋅π⋅
= 2
104
10
I
b) El oído humano es capaz de percibir sonidos desde intensidades muy bajas (10-12
W· m-2
)
hasta intensidades de 1 W· m-2
. Dado que el rango de intensidades audibles es muy amplio, se ha
introducido una escala logarítmica, la escala decibélica, para medir intensidades sonoras, que
además corresponde mejor con la sensibilidad del oído.
c) Para expresar la intensidad sonora en decibelios se utiliza la siguiente fórmula:
0
dB
I
I
log10⋅=β siendo I0 la intensidad umbral del oído humano, I0 = 10-12
W· m-2
Por lo tanto, para nuestro caso:
dB99
10
1095,7
log10 12
3
dB =
⋅
⋅=β −
−

ARAGÓN / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN A / CUESTIÓN 1
OPCIÓN A
1) Una partícula de masa m = 5 g oscila armónicamente a lo largo del eje OX en la forma
x = A cos ωt, con A = 0,1 m y ω = 20 π s-1
.
a) Determina y representa gráficamente la velocidad de la partícula en función del tiempo. (1 p.)
b) Calcula la energía mecánica de la partícula. (0,5 p.)
c) Determina y representa gráficamente la energía potencial de m en función del tiempo. (1
p.)
a) La ecuación que representa la velocidad en función del tiempo se obtiene derivando la ecuación
de la posición.
( )tπ20senπ2v;tωsenωA
dt
dx
v −=−==
v
2π
0,025 s 0,075 s 0,125 s t
0,05 s 0,1 s
-2π
b) La energía mecánica será la suma de la energía cinética y de la potencial:
( ) ( ) ( ) ( ) ( )( )
Jπ01,0π4·05,0
2
1
Aωm
2
1
E
tπ20costπ20senAωm
2
1
tπ20cosAωm
2
1
tπ20senωAm
2
1
E
kx
2
1
mv
2
1
EEE
2222
M
222222222
M
22
PCM
===
+=+−=
+=+=
c) La energía potencial es: ( ) ( )tπ20cosπ01,0tωcosAωm
2
1
E 22222
P ==
Como se trata de un coseno al cuadrado, todos sus valores serán positivos y la forma de la función
será igual que la del coseno pero con los tramos negativos simétricos respecto al eje OX
Esta función toma sus valores máximos en intervalos de tiempo de 0,05 s y se anula en los valores
de tiempo intermedios.
Máximos: t = 0; t = 0,05; t = 0,1; t = 0,15;…
Mínimos: t = 0,025; t = 0,075; t = 0,125;…

ARAGÓN / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
EP
0,01π2
t
0,025 0,05 0,075 0,1

/ OPCIÓN B / CUESTIÓN 1
CUESTIÓN 1
1) Un cuerpo de masa m = 0,1 kg oscila
armónicamente a lo largo del eje OX. En la
figura se representa su velocidad en función del
tiempo.
a) Determina y representa gráficamente la
posición (elongación) de la partícula en
función del tiempo. (1,5 puntos)
b) Calcula las energías cinética y potencial de
la partícula en el instante t = 0,05 s. (1 punto)
a) Para poder representar la elongación en función del tiempo, hay que conocer previamente los
valores de la amplitud A y la frecuencia angular ω.
Del valor máximo de la velocidad obtenemos el producto de ambas magnitudes: A· ω = 2
La frecuencia angular esta relacionada con el periodo mediante la expresión:
T
π2
ω =
Calculamos el periodo a partir de la gráfica contando el tiempo que pasa entre dos momentos
consecutivos de la onda dibujada que estén en fase. T = 0,4 s.
m127,0
π5
2
A
s/radπ5
4,0
π2
ω
==
==
Ya podemos representar la elongación teniendo en
cuenta que cuando la velocidad es máxima la
elongación es nula y cuando la elongación es máxima
la velocidad es nula. Como el movimiento comienza
con la velocidad en su estado máximo y decreciendo,
la partícula se encuentra en el punto de equilibrio y se
desplaza hacia su máxima elongación
2
v
0,127
-0,127 0,1 0,2 0,3 0,4 0,5 0,6
x
-2
b) A partir de los datos que tenemos construimos las ecuaciones de la elongación y la velocidad.
( )
( ) s/m2
4
π
cos205,0v;tπ5cos2v
m
π5
2
4
π
sen
π5
2
05,0x;tπ5sen
π5
2
x
===
===

/ OPCIÓN B / CUESTIÓN 1
Necesitamos también conocer el valor de la constante de recuperación. Lo obtenemos a partir del
producto de la masa por la frecuencia angular.
( ) m/Nπ5,2π5·1,0ωmk 222
===
Sustituimos en las expresiones de las energías:
( )
J1,0
π5
2
·π5,2·
2
1
kx
2
1
E
J1,02·1,0·
2
1
mv
2
1
E
2
22
P
22
C
=⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==
===
En el instante dado coinciden los valores de las energías cinética y potencial.

ZARAGOZA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 1
1. Una onda armónica transversal se propaga en el sentido positivo del eje OX y tienen
las siguientes características: amplitud 3 cm; longitud de onda, 2 cm; velocidad de
propagación, 2 m/s; la elongación del punto x = 0 en el instante t = 0 es de 3 cm.
a) Calcula el número de ondas y la frecuencia angular de esta onda, y escribe su
ecuación (1,5 puntos.)
b) Dibuja el perfil de la onda en t = 0,01 s. Indica un punto en el que sea máxima la
velocida de movimiento y otro en el que sea máxima la aceleración. (1 punto)
a) El número de ondas es: 1-
m314
02,0
·2·2
k =
π
=
λ
π
=
La frecuencia angular se relciona con la velocidad de propagación y la longitud de onda:
1-
s·rad6282·314· vk
v
··2··2 ===
λ
π=νπ=ω
Introduciendo esto en la ecuación tenemos: y(x, t) = 0,03 · sen (314 · x - 628 · t + φ)
y(0, 0) = 0,03 · sen φ = 0,03; φ =
2
π
Finalmente la ecuación queda: y(x, t) = 0,03 · sen (314 · x - 628 · t +
2
π
)
b) Dibujo

PDO. ASTURIAS / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN 2
OPCIÓN 2
1.- Comenta si la siguiente afirmación es verdadera o falsa: “En un movimiento
armónico simple dado por x = A senωt las direcciones y sentidos de la velocidad y la
aceleración coinciden en todos los puntos de la trayectoria” (1,2puntos)
2.- Un objeto oscila según un movimiento armónico simple dado por x = Asenωt. Si el
valor de la amplitud de la oscilación es 6 cm y la aceleración del objeto cuando
x = - 4 cm es 24 cm/s2
, calcular: (a) La aceleración cuando x = 1 cm (b) la velocidad
máxima que alcanza el objeto (1,3 puntos).
1. La afirmación es falsa, ya que como viene esquematizado en los dibujos, la aceleración y
la velocidad solo coinciden en dirección y sentido cuando el cuerpo se dirige hacia la
posición de equilibrio. Cuando el cuerpo se aleja de dicha posición la aceleración cambia
de sentido haciendo que la velocidad del cuerpo disminuya hasta detenerse en el extremo de
la trayectoria.
a a
v v
- A 0 A
a a
v v
- A 0 A
2 (a) Calculamos en primer lugar el valor de la pulsación ω a partir del dato de la
aceleración en x = - 4 cm.
122
s6ωs6
4
24
x
a
ω −−
=⇒=
−
−
=
−
=
Sustituyendo para x = 1 cm = 0,01 m.
22
s/m06,001,0·6xωa =−=−=
(b) Para calcular la velocidad máxima escribimos la ecuación del movimiento y derivamos
obteniendo la de la velocidad.
t6cos606,0
dt
dx
v;t6sen06,0x ===
el valor máximo se obtiene cuando el coseno vale la unidad, de modo que:
s/m606,0vmax =

PRINCIPADO DE ASTURIAS / SEPTIEMBRE 04. LOGSE / FÍSICA /
VIBRACIONES Y ONDAS / OPCIÓN 3
Opción 3
1.- Discute razonadamente si la siguiente afirmación es verdadera o falsa:
“Una explosión gigantesca que tuviera lugar en la Luna se oiría en la Tierra con una
intensidad muy pequeña porque la distancia Tierra-Luna es muy grande”.
2.- Una onda armónica que se propaga transversalmente por una cuerda tiene una
velocidad de propagación de 12,4 m/s. Una partícula (o segmento infinitesimal) de la
cuerda experimenta un desplazamiento máximo de 4,5 cm y una velocidad máxima de
9,4 m/s.
Determinar (a) la longitud de onda y (b) la frecuencia.
1. La afirmación es falsa.
El sonido es una onda que se clasifica como mecánica porque necesita un medio material
para su propagación. Entre la Tierra y la Luna no existe ningún medio material continuo
que permita esta propagación, de modo que el sonido no llegaría nunca a la Tierra.
2. La velocidad máxima de propagación se obtiene de la constante que multiplica a la
función sinusoidal que describe su movimiento:
Hz25,33
π2
9,208
π2
ω
fs/rad9,208
045,0
4,9
A
v
ω
ωAv;tωsenωAvtωcosAx
max
max
===⇒===
=−=⇒=
A partir de la frecuencia calculamos el periodo y con éste y la velocidad de propagación
podemos despejar la longitud de onda.
m0373,003,0·4,12Tvλ
T
λ
v;s03,0
f
1
T pp ===⇒===

Opción 2
1.- Deducir las expresiones de las energías asociadas al oscilador armónico simple.
2.-Se observa que un determinado muelle se alarga en 3,9 cm cuando se cuelga de él
una masa de 10 gr. Si una masa de 25 gr. unida a este muelle oscila en un movimiento
armónico simple, calcular el período de la oscilación.
1. La expresiones de las energías son:
22
pcT
2
p
2
c
kx
2
1
mv
2
1
EEE
kx
2
1
E
mv
2
1
E
+=+=
⎪
⎪
⎭
⎪⎪
⎬
⎫
=
=
Las ecuaciones de la velocidad y la posición son:
tωsenωAvtωsenωAv
tωcosAxtωcosAx
2222
222
=−=
==
Sustituyendo en cada una de las expresiones tenemos:
)φtω(senAωm
2
1
mv
2
1
E 0
2222
c +==
)φtω(cosAωm
2
1
kx
2
1
E 0
2222
p +==
( )
22
T
2222222222
T
Aωm
2
1
E
tωcostωsenAωm
2
1
tωcosAωm
2
1
tωsenωmA
2
1
E
=
+=+=
2. Aplicando la Ley de Hooke al muelle calculamos el valor de la K con los primeros datos:
m/N5,2
039,0
8,9·01,0
x
mg
KKxmg;KxF ===⇒==
Igualando las fórmulas proporcionadas por la segunda ley de Newton y la ley de Hooke
obtenemos la expresión de la que sale el valor de la frecuencia angular.
22
2
ωmKxωmKx
xωmF;amF
xKF
=⇒−=−
⎪⎭
⎪
⎬
⎫
−==
−=
rrrr
rr

El dato que necesitamos es el periodo de modo que:
sπ2,0
K
m
π2T
T
π2
mK
2
==⇒⎟
⎠
⎞
⎜
⎝
⎛
=

Opción 3
1.- Una onda transversal en una cuerda está descrita por la función y = 0,12
sen(πx/8 + 4πt) (expresada en unidades del SI). Determinar la aceleración y
la velocidad transversales en t = 0,2 s para un punto de la cuerda situado en
x = 1,6 m. (1,2 puntos).
2.- Una visión simplificada de los efectos de un terremoto en la superficie
terrestre, consiste en suponer que son ondas transversales análogas a las
que se producen cuando forzamos oscilaciones verticales en una cuerda. En
este supuesto y en el caso en que su frecuencia fuese de 0,5 Hz, calcular la
amplitud que deberían tener las ondas del terremoto para que los objetos
sobre la superficie terrestre empiecen a perder el contacto con el suelo (1,3
puntos).
RESPUESTA:
1. Calculamos las expresiones de la velocidad y de la aceleración derivando
sucesivamente la posición.
( ) ⎟
⎠
⎞
⎜
⎝
⎛
+−==
⎟
⎠
⎞
⎜
⎝
⎛
+==
t4x
8
sen12,0·4
dt
dv
a
t4x
8
cos12,0·4
dt
dy
v
2
π
π
π
π
π
π
Sustituimos los valores dados:
( )
( ) ( ) 22
s/m0sen12,0·42,0;6,1a
s/m48,0cos12,0·48,0
8
6,1
cos12,0·42,0;6,1v
=−=
−==⎟
⎠
⎞
⎜
⎝
⎛
+=
ππ
ππππ
π
π

2. Para que los objetos de la superficie terrestre pierdan contacto con el suelo se deben
ver sometidos a una fuerza hacia arriba que debe ser igual a su peso o superior, por lo
tanto la aceleración del movimiento ondulatorio debe ser mayor que g.
A partir de la ecuación del movimiento ondulatorio obtenemos la de la aceleración
( ) ( )
( ) ( ) ( )
( ) ( ) ( )KxtsenA
dt
t,xdv
t,xa
KxtcosA
dt
t,xdy
t,xv
KxtsenAt,xy
2
−−==
−==
−=
ωω
ωω
ω
Igualamos el valor de la aceleración máxima al de la gravedad.
( )
m2,39
5,0
8,9g
AgA 22
2
===⇒=
ω
ω

PRINCIPADO DE ASTURIAS / SEPTIEMBRE 05. LOGSE / FÍSICA / VIBRACIONES
Y ONDAS / OPCIÓN 2
Opción 2
1.- Explica el fenómeno de resonancia (1,2 puntos).
2.- Sea un movimiento armónico simple, dado por x = Asen(ωt +φ), con
frecuencia angular ω = 0,4 s-1, en donde, para t = 0 la posición y velocidad
de la partícula son 0,2 cm y 2 cm/s respectivamente. Calcular la amplitud de
las oscilaciones y la fase inicial. (1,3 puntos)
RESPUESTA:
1. Las oscilaciones de los cuerpos son normalmente amortiguadas porque se disipa
energía. Para que un cuerpo o sistema amortiguado oscile indefinidamente hay que ir
suministrándole energía. En este caso decimos que el oscilador es forzado.
Cuando comunicamos al sistema más energía de la que se pierde aumenta su
amplitud. De este modo podemos aumentar la energía comunicada hasta llegar a la
magnitud deseada y mantener la energía en ese punto de modo que se pierde la misma
que se gana y la amplitud se mantiene constante.
Cada sistema tiene una frecuencia natural de oscilación, por ejemplo en el caso del
muelle es conocida y fácil de calcular, vale:
m
K
=ω
Cuando la frecuencia a la que comunicamos energía a un sistema coincide con la
frecuencia natural del sistema, la amplitud de la oscilación se hace mucho más grande
que la amplitud de la fuerza que comunica la energía. Este es el fenómeno de la
resonancia. La energía que absorbe el oscilador se hace máxima. La frecuencia
natural a la que ocurre este fenómeno se denomina también frecuencia de resonancia.
2. Escribimos los datos en unidades del Sistema Internacional y sustituimos en las
ecuaciones formando un sistema:
( ) ( )
⎭
⎬
⎫
=
=
+=+=
φ
φ
φωωφω
cos4,0·A02,0
Asen002,0
tcosAv;tAsenx
Dividiendo ambas ecuaciones
( ) º29,204,0arctg;04,0tg;
cos4,0·A
Asen
02,0
002,0
==== φφ
φ
φ
Sustituyendo en cualquiera de las ecuaciones
m05,0A;29,2sen·A002,0 ==

ASTURIAS / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN 2
Opción 2
1.- Analiza el comportamiento de un péndulo simple y discute cómo puede ser utilizado
para la determinación de g. (1,2puntos)
2.- Una partícula oscila según un movimiento armónico simple de 8 cm de amplitud y 4 s
de período. Calcula su velocidad y aceleración en los casos: (a) Cuando la partícula pase
por el centro de oscilación. (b) Medio segundo después que la partícula haya pasado por
uno de los extremos de su trayectoria (1,3 puntos).
1. Para el péndulo de la figura, tenemos las siguientes ecuaciones en cada eje.
Eje y: T + Py = m·an
Eje x: Px = m·ax
Tomando: P = mg; Px = mg sen θ; Py = mg cos θ
La expresión del eje x puede escribirse:
xamsengm /=θ/
Para ángulos muy pequeños, sen θ = θ, la ecuación queda:
g·θ = ax
θ
T
Px
Py
P
Si la longitud del péndulo es L, como el ángulo es pequeño, puede sustituirse el arco por el
desplazamiento:
q·L = x ⇒ x
L
g
ax −=
Comparando este valor con el de la aceleración de un m.v.a.s.
L
g
T
4
L
g
;xa 2
2
22
=
π
=ωω−=
Despejando el periodo:
g
L
2T π=
Luego para calcular g lo que hay que hacer el calcular el periodo del péndulo medir su longitud e
introducir los datos en la fórmula obtenida.
2. Escribimos la ecuación del m.v.a.s.
2
t
cos08,0t
4
2
cos08,0)tcos(Ax
π
=
π
=ω=
Derivando se obtienen las ecuaciones de la velocidad y de la aceleración.
2
t
cos
2
08,0a;
2
t
sen
2
·08,0v
2
π





 π
−=
ππ
−=
a) Cuando pasa por el centro de oscilación, x = 0
π+
π
=
π
=
π
n
22
t
;0
2
t
cos

Tomamos únicamente la primera solución, t = 1 s.
s/m126,0
2
08,0
2
sen
2
08,0v =
π
−=
ππ
−=
a = 0 porque el 0
2
cos =
π
b) Cuando pasa por un extremo, x = 0,08 m.
π+=
π
⇔=
ππ
= n0
2
t
1
2
t
cos;
2
t
cos08,008,0
Tomando solo la primera solución, t = 0. Como nos piden los resultados medio segundo después,
tomamos t = 0,5 s.
s/m089,0
4
2
08,0
4
sen
2
08,0v −=
π
−=
ππ
−=
2
22
s/m14,0
8
2
08,0
4
cos
2
08,0a =
π
−=
π





 π
−=

Opción 3
1.- ¿Qué se entiende por difracción y en qué condiciones se produce? (1,2 puntos)
2.- ¿ Cuál debería ser la distancia entre dos puntos de un medio por el que se propaga
una onda armónica, con velocidad de fase de 100 m/s y 200 Hz de frecuencia, para que
se encuentren en el mismo estado de vibración? (1,3 puntos)
1. La difracción es el cambio en la dirección de propagación que sufre una onda sin cambiar de
medio. Este hecho se produce cuando el movimiento ondulatorio se encuentra un obstáculo en su
camino cuyas dimensiones son del mismo orden o menores que la longitud de onda.
El principio de Huygens en el que cada punto del frente de ondas actúa como emisor de ondas
elementales, permite explicar gráficamente este fenómeno.
En todo momento los puntos del frente de ondas emiten ondas que al interferir con las emitidas
por los puntos de los alrededores forman el frente de ondas plano que se observa. Al llegar a la
abertura los puntos del frente de ondas que pasan ella actúan como emisores de ondas. Estas
ondas al no interferir con otras generadas por otros puntos, cambian la forma de su frente de
ondas, pasando este de ser plano a ser circular.
2. Para que dos puntos se encuentren en el mismo estado de vibración debe haber entre ellos un
número entero de longitudes de onda. Calculamos entonces el valor de la longitud de onda.
mT100s/m100
T
ve =λ⇒=
λ
=
Como s10·5THz200
T
1
f 3−
=⇒==
Luego m5,010·5·100 3
==λ −
Los puntos deben estar a 0,5 m, o a distancias cuyo valor sea un múltiplo entero de 0,5.

ASTURIAS / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/PR.2
Al pulsar una cuerda de guitarra, inicialmente en reposo, ésta vibra de tal modo que cada
uno de sus puntos comienza a moverse en trono a su posición inicial según la dirección
perpendicular a la determinada inicialmente por la propia cuerda. Decimos entonces que
en la cuerda se produce una onda armónica. a) ¿Qué tipo de movimiento describe cada
uno de los puntos de la cuerda? b) ¿Cómo se llaman los puntos de la cuerda que no
vibran (es decir, en los que la perturbación es nula en todo instante)? c) Como mínimo,
¿cuántos puntos de este tipo hay? d) ¿Existen instantes en los que todos los puntos de la
cuerda tienen la misma velocidad? En caso afirmativo, ¿cuál es el valor de dicha
velocidad?
a) Todos los puntos de la cuerda describen un movimiento armónico simple, de manera que el
conjunto tiene forma de onda armónica estacionaria.
b) Los puntos que no vibran se llaman nodos, y se caracterizan porque la amplitud de su
oscilación es cero.
c) Puesto que la cuerda está enganchada por dos puntos, habrá un mínimo de dos nodos en la
onda.
d) Cuando la onda es única, existe un instante en el que la velocidad de todos los puntos es cero.
Este instante coincide con el de máxima amplitud de la oscilación para todos lo puntos.

ASTURIAS / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS/PR. 2
Bloque 2.- a) obtener la frecuencia de las oscilaciones de un amasa m unida a un resorte
de constante elástica k.
b) Un cuerpo de masa m = 0,1 kg está sujeto a un muelle de constante elástica k = 50
N/m. Se estira 5 cm y se pide:
b1) La energía potencial de la masa por estar unida al resorte.
b2) La velocidad máxima que adquiere el cuerpo una vez que se deja en libertad.
b3) La frecuencia de las oscilaciones.
a) Una oscilación tiene la forma: x = A · sen(ω · t)
Fuerza en este movimiento es: F = m · a = -m · A · ω2
· sen(ω · t) = - m · ω2
· x = - k · x
Por tanto:
m
k
=ω
b1) La energía potencial es: E =
2
1
· k · x2
=
2
1
· 50 · 0,052
= 0,0625 J
b2) La máxima velocidad será aquella que iguale en energía a la potencial:
2
1
· m · v2
= Ep max
Por tanto: m/s14,1
1,0
0,065·2
m
E·2
v
maxp
===
b3) La frecuencia de la oscilación es: Hz36,22
1,0
50
m
k
===ω

ASTURIAS / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN 3
Opción 3
1.- Una onda electromagnética que se propaga en el vacío tiene una longitud de onda de
5·10-7
m. Calcular su longitud de onda cuando penetra en un medio de índice de
refracción: n = 1,5. ( 1,2 puntos)
2.- La ecuación de una onda transversal que se propaga por una cuerda, expresada en
unidades del SI es: y = 0,03 sen(2,2x - 3,5t).
Calcular:
a) Su velocidad de propagación, longitud de onda y frecuencia
b) ¿Cuál es el desplazamiento máximo de cualquier segmento de la cuerda?
c) ¿Cuál es la velocidad máxima de cualquier segmento de la cuerda?.
(1,3 puntos)
1. De una onda em, lo único que nunca cambia es su frecuencia:
s/m10·2
5,1
10·3
5,1
c
v;
v
c
5,1n 8
8
m
m
=====
como v = λ f, calculamos el valor de su frecuencia:
Hz10·6
10·5
10·3c
f 14
7
8
==
λ
=
Aplicando la misma ecuación en el medio material:
m10·3,3
10·6
10·2
f
v
;fv 7
14
8
−
===λλ=
2a. Fijándonos en los datos de la ecuación:
m86,2
2,2
2
K
2
;
2
K =
π
=
π
=λ
λ
π
=
Hz56,0
8,1
1
fm80,1
5,3
22
T;
T
2
==⇒=
π
=
ω
π
=
π
=ω
s/m6,156,0·86,2fvp ==λ=
2b. El desplazamiento máximo coincide con la amplitud, que es: A = 0,03 m = 3 cm
2c. Derivando con respecto al tiempo se tiene:
)t5,3x2,2cos(105,0)t5,3x2,2cos(03,0·5,3)t,x(v −−=−−=
La velocidad máxima es vmax = 0,105 m/s

OVIEDO / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIOENS Y ONDAS / OPCIÓN A/ Nº 3
3. a) ¿Qué es una onda estacionaria? ¿Cuáles son sus características principales?
Exponer algún fenómeno cotidiano que tenga que ver con ondas estacionarias.
b) Las ondas de televisión, ¿son estacionarias o de propagación? ¿Son longitudinales o
transversales? ¿Necesitan un medio como el aire para propagarse o también se
propagan en el vacío? ¿Su longitud de onda es mayor o menor que la longitud de onda
de la luz visible?
a) Una onda estacionaria es un movimiento oscilatorio que está confinado en el espacio y que
no se propaga. Las ondas estacionarias surgen como la interferencia de dos ondas iguales que se
propagan en sentidos contrarios. Sus principales características son su frecuencia y longitud de
onda, ambas relacionadas entre sí por la velocidad de la onda en el medio, y la amplitud de la
onda estacionaria. Finalmente se puede considerar el valor de la onda estacionaria en los
extremos de la misma, si se trata de puntos fijos o no.
Las ondas estacionarias tienen lugar en tódos los instrumentos musicales, como guitarras,
pianos, flautas, etc.
b) Las ondas de televisión son ondas electromagnéticas que se propagan. Las ondas
electromagnéticas son ondas transversales que se propagan en medios materiales y en el vacío.
Finalmente, su longitud de onda es mayor que la de la luz visible.

ASTURIAS / SEPTIEMBRE99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/PR. 2
Un terremoto produce ondas longitudinales y ondas transversales. a) ¿En qué se
diferencian ambos tipos de ondas? b) En la corteza terrestre, las primeras se propagan
con una velocidad de 8,0 km/s mientras que las segundas lo hacen a 5,0 km/s; si en un
observatorio sísmico los dos tipos de ondas se reciben con 200 s de diferencia temporal,
determínese la distancia del observatorio al hipocentro del terremoto. c) Si el período de
ambas ondas es de 0,55 s, determínese sus frecuencias y longitudes de onda.
a) En las ondas longitudinales la vibración se realiza en la dirección de la propagación, mientras
que las vibraciones transversales tienen lugar perpendicularmente a ella.
b) La onda longitudinal tarda:
L
L
v
d
t = , la transversal:
T
T
v
d
t = .
La diferencia de tiempos es:
LT
LT
v
d
v
d
ttt −=−=∆
Despejando y sustituyendo se obtiene la distancia al hipocentro del terremoto:
km6672
8
1
5
1
·200
v
1
v
1
·td
11
LT
=





−=





−∆=
−−
c) La longitud de onda se relaciona con la velocidad según: λ = v · T, mientras que la frecuencia
es la inversa del periodo. Por tanto:
λT = vT · T = 5 · 0,55 = 2,75 km
νT = T-1
= 0,55-1
= 1,82 Hz
Para la longitudinal se tiene:
λL = vL · T = 8 · 0,55 = 4,4 km
νL = T-1
= 0,55-1
= 1,82 Hz

ASTURIAS / SEPTIEMBRE99. COU / FÍSICA / VIBRACIONES Y ONDAS/PR. 1
En aguas profundas, la velocidad v de las olas del mar y su longitud de onda se
relacionan así:
v =
p·2
1
gα
· λβ
donde g es la aceleración de la gravedad
a) Obtener los valores de α y β mediante Análisis Dimensional.
b) Al cuadruplicar la velocidad de las olas ¿cómo variará la longitud de onda?
a) La velocidad tiene unidades de longitud dividido por tiempo, la gravedad es aceleración
(espacio/tiempo2
) y la longitud de onda es distancia, por tanto:
α
β+αβ
α
π
=





π
= ·22
T
1
·L·
·2
1
L·
T
L
·
·2
1
T
L
Resolviendo el sistema se tiene:
Por el tiempo: 1 = 2 · α; α =
2
1
Por el espacio: 1 = α + β; β = 1 – α = 1 -
2
1
=
2
1
Por tanto la ecuación es:
π
λ
=
·2
·g
v
b) Si la velocidad se hace 4 · v0, puesto que la longitud de onda es proporcional a la velocidad al
cuadrado, se tendrá λ = 16 · λ 0.

ASTURIAS / SEPTIEMBRE99. LOGSE / FÍSICA / OPTICA/PR. 3
a) Un recipiente cúbico de paredes opacas y 25 cm de lado, con sus caras orientadas
hacia los puntos cardinales, está abierto en su parte superior y se coloca sobre una
superficie horizontal. El Sol está situado en la dirección Sur, de modo que los rayos que
provienen del mismo e inciden sobre el recipiente forman 60º con la horizontal. ¿Qué
longitud tiene la sombra formada en el fondo del recipiente por la pared vertical del
mismo? Si posteriormente se llena de agua con índice de refracción 1,33 hasta 20 cm de
altura, ¿en cuánto aumenta o disminuye la longitud de la sombra anterior? b) ¿Qué es el
arco iris? Explíquese su formación.
a) El esquema del problema es el de la figura.
La sombra tiene un tamaño de: cm43,14
60tg
25
LS ==
Tras llenar de agua, el ángulo con que incide la luz se obtiene con la ley de
Snell: ni · sen αi = nt · sen αt, en la que los ángulos se miden respecto a la
normal. Por tanto: º1,22376,0
33,1
º30sen
sen tt =α⇒==α
Finalmente: β = 90º - ατ = 67,9º
Por tanto la zona de sombra es:
cm01,11
º9,67tg
20
º60tg
5
LS =+=
La diferencia de longitud en las sombras es de 3,42 cm.
LS
25 cm
60º
20 cm
60ºβ

ISLAS BALEARES / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN B / PROBLEMA 1
PROBLEMA 1
P1. Una onda sinusoidal avanza con una velocidad de 32 m/s desde un punto que
consideramos el origen del eje x. La amplitud de la onda es 5 cm y la frecuencia
de 50 Hz
a) Calcula la longitud de onda
b) Escribe la ecuación de la onda
c) Determina la elongación en un punto situado en x = 50 cm en el instante
t = 2,6 s
a) La velocidad de la onda se calcula a partir del producto de su longitud de onda por la
frecuencia. Despejando de la misma el valor de la longitud de onda se tiene:
m64,0
50
32
f
v
λ;f·λv ====
b) La ecuación de una onda que avanza en el sentido positivo del eje x viene dada por la
expresión:
( )kxtωsenA)t,x(y −=
Calculamos el valor de ω y k:
s/radπ100fπ2ω ==
1
m817,9
64,0
π2
λ
π2
k −
===
Sustituyendo tenemos la ecuación de la onda:
( )x817,9tπ100sen05,0)t,x(y −=
c) Se sustituyen los valores dados en la ecuación de la onda:
( ) m05,0049,098,0·05,05,0·817,96,2·π100sen05,0)6,2;5,0(y ≈==−=
el punto se encuentra en su estado de máxima elongación

ONDAS / OPCIÓN B / ACTIVIDAD 5
OPCIÓN B
P-1. En un medio elástico se establece un movimiento ondulatorio descrito
por la ecuación y (x,t) = 0,02 sen ( 10πx + 30πt ) en unidades del sistema
internacional. Determina:
a) La longitud y la frecuencia de esta onda
b) La velocidad de propagación y el sentido en que lo hace.
c) La velocidad máxima con la que oscila un punto del medio por el que
se propaga la onda.
RESPUESTA:
a) Comparando la ecuación dad con la ecuación general de un movimiento
ondulatorio:
( )kxtωsenA)t,x(y −=
m2,0
5
1
π10
π2
K
π2
λ
λ
π2
K ====⇒=
La frecuencia es el inverso del periodo:
Hz15
2
30
ν
30
2
π30
π2
ω
π2
T
T
π2
ω
==
===⇒=
b) La velocidad de la onda la calculamos conociendo el tiempo que tarda en avanzar
una longitud de onda:
s/m3
15
1
5
1
T
λ
v ===
La onda se desplaza de derecha a izquierda porque el signo de la fase es negativo.
c) Derivamos para obtener la velocidad de vibración:
)tπ30xπ10·cos(02,0·π30
dt
)t,x(dy
)t,x(v +==
La velocidad se hace máxima cuando el coseno vale la unidad, de modo que:
vmax = 0,6 π m/s

OPCIÓN A
Q1. Las ondas se pueden clasificar como longitudinales y transversales. Decir qué
característica las diferencia y dar un ejemplo de cada uno de estos tipos de ondas.
Las ondas transversales y longitudinales son las que se clasifican atendiendo a su dirección
de propagación.
Las longitudinales son aquellas en las que la dirección de propagación coincide con la
dirección de vibración. Son ondas longitudinales las del sonido o las que se propagan en un
muelle cuando vibra longitudinalmente.
dirección en que tiene lugar la vibración. Son ondas transversales las ondas
electromagnéticas y las ondas sísmicas.

ISLAS BALEARES / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN A / PROBLEMA 1
Dada la ecuación de ondas tridimensional:
y = 0,04 · sen(2,0 · x – 3,14 · t + 2,0)
con y, x medidas en metros y t en segundos, calcula:
a) La longitud de onda y la frecuencia de esta onda.
b) La velocidad máxima, en módulo, de oscilación de las partículas del medio por el cual
se propaga la onda.
c) Si la onda fuese transversal y dijésemos que está polarizada, ¿que querríamos decir?
Razona la respuesta.
a) La ecuación general de una onda es: 





ϕνπ
λ
π
= 0-· t··2-· x
·2
sen·Ay
Identificando términos se tiene que: 2
·2
=
λ
π
, por tanto: λ = 3,14 m.
Por otra parte, 2 · π · ν = 3,14, por tanto ν = 0,2 s-1
.
b) La velocidad de la ondas es la derivada de la amplitud:
vy = -0,04 · 3,14 · cos (2,0 · x – 3,14 · t + 2,0)
Por tanto la velocidad máxima será: vy max = 0,1256 m · s-1
c) En las ondas transversales el movimiento de las partículas en el medio es perpendicular a la
dirección de propagación de la onda. La polarización indica que el movimiento transversal de las
partículas se realiza en un único plano.

ISLAS BALEARES / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A
/ PREGUNTA 1
Dada la ecuación de ondas tridimensional:
y = 0,04 · sen(2,0 · x – 3,14 · t + 2,0)
con y, x medidas en metros y t en segundos, calcula:
a) La longitud de onda y la frecuencia de esta onda.
b) La velocidad máxima, en módulo, de oscilación de las partículas del medio por el cual
se propaga la onda.
c) Si la onda fuese transversal y dijésemos que está polarizada, ¿que querríamos decir?
Razona la respuesta.
a) La ecuación general de una onda es: 





ϕνπ
λ
π
= 0-· t··2-· x
·2
sen·Ay
Identificando términos se tiene que: 2
·2
=
λ
π
, por tanto: λ = 3,14 m.
Por otra parte, 2 · π · ν = 3,14, por tanto ν = 0,2 s-1
.
b) La velocidad de la ondas es la derivada de la amplitud:
vy = -0,04 · 3,14 · cos (2,0 · x – 3,14 · t + 2,0)
Por tanto la velocidad máxima será: vy max = 0,1256 m · s-1
c) En las ondas transversales el movimiento de las partículas en el medio es perpendicular a la
dirección de propagación de la onda. La polarización indica que el movimiento transversal de las
partículas se realiza en un único plano.

ISLAS BALEARES / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN B
/ CUESTIÓN 1
Dos ondas que se propagan en dos medios diferentes con ecuaciones de propagación:
a) y1 = 3 · cos(4 · x + 2 · t)
b) y2 = 2 · sen (3 · x – 4 · t)
Con y medido en milímetros, t en segundos y x en metros.
a) ¿Cuál de las dos tiene la velocidad de propagación mayor?
b) ¿Cuál de las dos comunica a las partículas del medio correspondiente velocidades
mayores?
Razona las respuestas.
a) La velocidad de propagación de una onda es:
kT
v
ω
=
λ
=
Por tanto son: 1-
1 s·m5,0
4
2
v −=
−
= y 1-
2 s·m33,1
3
4
v == .
Por tanto la velocidad de propagación de la segunda onda es mayor.
b) La velocidad del medio es la derivada de la ecuación de ondas:
vy1 = -3 · 2 · sen (4 · x + 2 · t) = -6 · sen (4 · x + 2 · t); vy1 max = 6 mm · s-1
vy2 = 2 · 4 · cos (3 · x - 4 · t) = 8 · sen (3 · x - 4 · t); vy2 max = 8 mm · s-1
La velocidad de las partículas del medio es mayor en la segunda.

ISLAS BALEARES / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN A / PROBLEMA 2
OPCIÓN A
P2. Por una cuerda se propaga una onda que está descrita por la ecuación:
y(x, t) = 0,04·sen (x + 5t) en unidades del S.I. Determinar:
a) La velocidad de propagación de la onda.
b) El primer valor de t para el que se anula la velocidad en el punto x = 1 m.
c) La aceleración de un punto de la cuerda situado a x = 1 m en el instante t = 2 s
a) Comparando la ecuación dada con la ecuación general de una onda, se tiene:
( )
s/m5
5
π2
π2
T
λ
v
s
5
π2
ω
π2
T
T
π2
ω
mπ2
k
π2
λ
λ
π2
k
tωkxsenA)t,x(y
===






==⇒=
==⇒=
+=
b) Derivando la ecuación de la posición obtenemos la ecuación de la velocidad de vibración
de los distintos puntos de la onda.
( ) ( )t5xcos2,0t,xv +=
Igualamos el valor de la velocidad para x = 1m.
( ) s114,0
5
1
10
π
t;πn
2
π
t51t51cos2,00 ≈−=+=+⇔+=
c) Derivando la ecuación de la velocidad se obtiene la aceleración:
)t5x(sen)t,x(a +−=
Sustituyendo para x = 1 m y t = 2 s:
( ) 2
s/m19999,0)101(sen2,1a ≈=+−=

CANARIAS / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN B / CUESTIÓN 2
Cuestiones
2.- ¿Qué diferencia existe entre movimiento armónico simple y un movimiento
vibratorio?. Cita un ejemplo de cada uno de ellos.
Un movimiento es armónico simple cuando el sistema o cuerpo que lo realiza está sometido
a la ley de Hooke.
xωax·kF 2 rrrr
−=⇒−=
Para que el sistema pueda oscilar (vibrar) a uno y otro lado de la posición de equilibrio, es
necesario que además pueda almacenar algún tipo de energía potencial y poseer una masa
que le permita alcanzar energía cinética.
Es un ejemplo de movimiento armónico simple el que puede realizar un cuerpo suspendido
de un muelle.
Un movimiento vibratorio es un movimiento cualquiera de vaivén como puede ser el que
realiza la punta de la rama de un árbol cuando es empujada por la fuerza del viento

OPCIÓN B / CUESTIÓN 3
Cuestiones
3.- Describe en que consiste el experimento de Young. Comenta los resultados que se
obtienen y lo que demuestra dicha experiencia.
El experimento de Young consistió en superponer dos haces de ondas y comprobar que si
los máximos de estas ondas coincidían se producía un máximo de mayor valor y si lo que
coincidía era un máximo con un mínimo, el resultado era la suma de sus amplitudes,
pudiendo llegar a ser cero si eran del mismo valor. Curiosamente la primera demostración
no la realizó con ondas de luz sino en una cubeta de ondas.
Cuando el experimento se realiza con dos haces de luz estos deben ser monocromáticos y
coherentes, para ello lo primero que se hace es hacer incidir el haz sobre una rendija muy
pequeña y el rayo que parte de esta incide sobre una doble rendija. Las rendijas deben ser
muy pequeñas para que en ellas se pueda producir difracción.
La interferencia de las ondas secundarias producidas dio lugar a una imagen formada por
zonas claras y oscuras cuya forma dependía de la forma de las rendijas y su posición de la
distancia a estas.
Con ello demostró que luz + luz puede dar como resultado oscuridad demostrando así que
la naturaleza de la luz debía ser ondulatoria como las ondas del agua.

OPCIÓN B / PROBLEMA 1
PROBLEMAS
1.- Una partícula de 10g de masa oscila
armónicamente según la expresión x = A·sen
(ω·t). En la figura se representa la velocidad de
esta partícula en función del tiempo. Calcula:
a) La frecuencia angular, “ω”, y la amplitud,
“A”, de la oscilación
b) La energía cinética de la partícula en el
instante t1 = 0.5s, y la energía potencial en t2 =
0.75s
c) ¿Qué valor tiene la energía en los dos instantes
anteriores?
0 0.5 1 1.5
t (s)
-2
-1
0
1
2
v(m/s)
a) La ecuación de la velocidad que se representa en la gráfica se corresponde con la
función:
tω·cosωAv =
Como el movimiento se repite cada segundo, el periodo T = 1 s y la frecuencia que es el
valor inverso del periodo es f = 1 Hz, de modo que la frecuencia angular vale:
s/radπ2fπ2ω ==
Conocido el valor de la amplitud de la velocidad, despejamos el de la amplitud de la
posición:
m
π
1
π2
2
ω
2
A2ωA ===⇒=
b) Las expresiones de las energías cinética y potencial son:
tπ2sen·02,0tπ2sen
π
1
·π4·01,0
2
1
xωm
2
1
E
tπ2·cos02,0tπ2·cos2·01,0
2
1
mv
2
1
E
22
2
222
p
2222
c
===
===
Sustituyendo para los valores del tiempo dados:
J02,0π5,1sen·02,075,0·π2sen·02,0E
J02,0π·cos02,05,0·π2·cos02,0E
22
p
22
c
===
===
c) La energía total tiene un valor constante que es:
J02,0
π
1
·π4·01,0·
2
1
Aωm
2
1
E 2
222
T ===
Como el valor coincide con los obtenidos en cada uno de los instantes del apartado quiere
esto decir que en t = 0,5 s no hay elongación y por tanto toda la energía es cinética y en el

OPCIÓN B / PROBLEMA 1
instante
t = 0,75 s no hay velocidad y toda la energía es potencial

CANARIAS / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN 1 /
CUESTIÓN 1
Interpreta los fenómenos de reflexión y refracción de las ondas utilizando el principio de
Huygens.
La reflexión y la refracción tienen lugar cuando una onda incide sobre una frontera. Según el
principio de Huygens, cada punto de la frontera emite ondas secundarias que darán forma a la
onda reflejada y a la transmitida. El ángulo de reflexión es igual al de incidencia porque la longitud
de las ondas reflejadas y su velocidad es igual a la de las incidentes. El ángulo de transmisión es
diferente debido a la diferente velocidad de propagación de las ondas en el nuevo medio.

CANARIAS / SEPTIEMBRE 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN A
Cuestión 2
Explica la diferencia entre ondas longitudinales y transversales. Propón un ejemplo de
cada una de ellas.
Las ondas transversales, son aquellas en las que la dirección de propagación es perpendicular a la
dirección en que tiene lugar la perturbación. Son ondas transversales las ondas en la cuerda, las
ondas electromagnéticas y las ondas sísmicas S.
Las ondas longitudinales, son aquellas en las que la dirección de propagación coincide con la
dirección en que tiene lugar la perturbación. Son ondas longitudinales las que las que se propagan
en un muelle si desplazamos un trozo del mismo a lo largo de su longitud.

CANARIAS / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
Cuestión 2
2.- Explica la diferencia entre ondas longitudinales y ondas transversales. Propón un
ejemplo de cada una de ellas.
Las ondas transversales y longitudinales son las que se clasifican atendiendo a su dirección de
propagación.
Las longitudinales son aquellas en las que la dirección de propagación coincide con la dirección
de vibración. Son ondas longitudinales las del sonido o las que se propagan en un muelle cuando
vibra longitudinalmente.
dirección en que tiene lugar la vibración. Son ondas transversales las ondas electromagnéticas y
las ondas sísmicas s.

CANTABRIA / JUNIO 2000. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
CUESTIÓN B
CUESTIÓN B
Una onda transversal se propaga por una cuerda, siendo su ecuación (en unidades del
SI) y = 0,05 sen(4πt - 2πx). Se pide:
a) ¿Cuánto vale la velocidad de propagación de la onda?
b) ¿Cuál será la velocidad de un punto que se encuentra a 2 m del origen en el instante t
= 5 s?
a) La velocidad se define como v = ν λ = 2 · 1 = 2 m s-1
b) La velocidad del punto será la velocidad transversal de la onda, que es la derivada de la
posición de cada punto: vy =
dt
dy
= 0,05 · 4 π cos(4π t – 2π x)
vy = 0,05 · 4 π cos(4 π 5 – 2 π 2) = 0,2 π cos(16 π) = 0,628 m s-1

CANTABRIA / JUNIO 2000. SELECTIVIDAD / FÍSICA / VIBRACIONES Y
ONDAS / CUESTIÓN D
CUESTIÓN D
Una onda transversal (A) se propaga por un medio según la ecuación
y = 10-2
sen 10(100 t - x) en unidades del SI.
a) Escribe la ecuación de una onda transversal (B) que se propague con una longitud de
onda que sea el doble y se propague en el sentido contrario que la onda A y el resto de
los parámetros iguales.
b) Escribe la ecuación de una onda transversal (C) que se propague con una amplitud y
frecuencia que sean la mitad de A y el resto de los parámetros iguales.
a) La onda sería: y = 10-2
sen 10(100 t + x/2)
b) La onda sería: y = 5 · 10-3
sen 10(50 t + x)

CANTABRIA / JUNIO 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN DE PROBLEMAS Nº 2
2.1
Cierto muelle, que se deforma 20 cm cuando se le cuelga una masa de 1,0 Kg (Figura A),
se coloca sin deformación unido a la misma masa sobre una superficie sin rozamiento,
como se indica en la figura B. En esta
posición se tira de la masa 2,0 cm y
se suelta. Despreciando la masa del
muelle, calcular:
a) La ecuación de la posición para el
m.a.s. resultante.
b) Las energías cinética, potencial
elástica y mecánica total cuando ha
transcurrido un tiempo t = (3/4)T,
donde T es el período del m.a.s.
Datos: g = 9,8 m/s
a) De la ecuación general de un resorte elástico y con los datos aportados por el enunciado se
puede obtener la constante elástica.
N/m49
2,0
1·8,9
x
F
kx·kF ==
∆
=⇒∆=
El período de oscilación se calcula según la fórmula:
s89,0
49
1
2
k
m
2T =π=π=
Escribimos ecuación general del m.a.s. y se sustituyen los valores obtenidos:
t7sen·02,0)t
T
2
(sen·A)wt(sen·Ax =
π
==
b)
J0,0098EpEcEm
J0,0098Ep
0Ec
=+=
=










 π
==
=













 π
−=−=
2
2
2
222
7
2
·
4
3
·7sen·02,0·49·
2
1
x·k·
2
1
)
7
2
·
4
3
·7(sen·02,002,0·49·
2
1
)xA·(k·
2
1

CUESTIÓN A
PRIMERA PARTE
CUESTIÓN A
A. a) 1 PUNTO En un movimiento armónico simple, ¿cuál es la relación entre la energía
total y la amplitud?
b) 1 PUNTO Un oscilador armónico se encuentra en un momento dado en una
posición igual ala mitad de su amplitud (x = A/2), ¿cuál es la relación entre la
energía cinética y la energía potencial en ese momento?
a) La expresión de la energía total es:
22
pcT kx
2
1
mv
2
1
EEE +=+=
Las ecuaciones de la velocidad y la posición son:
tωsenωAvtωsenωAv
tωcosAxtωcosAx
2222
222
=−=
==
Sustituyendo en la expresión de la energía tenemos:
( )
22
T
2222222222
T
Aωm
2
1
E
tωcostωsenAωm
2
1
tωcosAωm
2
1
tωsenωmA
2
1
E
=
+=+=
Luego podemos concluir que la energía total depende del cuadrado de la amplitud.
b) Para que la posición sea igual a la mitad de la amplitud:
rad
6
π
tω;
2
1
tωcos
2
A
tωcosA ===
Para ese valor de la fase, la velocidad es:
4
ωA3
2
3ωA
6
π
senωAv
22
=−=−=
La relación entre ambas energías es:
3
4
1
4
3
4
A
ωm
2
1
4
ωA3
m
2
1
E
E
2
2
22
p
c
===
La energía cinética es tres veces mayor que a energía potencial.

CUESTIÓN C
PRIMERA PARTE
CUESTIÓN C
C. Se considera un vaso cilíndrico lleno de agua hasta el borde.
En el fondo hay un espejo plano. Un rayo de luz monocromática
incide con un ángulo de 30º sobre la superficie. El rayo llega al
espejo del fondo, se refleja y vuelve a salir a la superficie.
a) 0,25 PUNTOS Completa el esquema adjunto de la marcha del
rayo.
b) 0,75 PUNTOS Calcular el ángulo que se ha desviado en total el
rayo incidente.
c) 1 PUNTO ¿Para algún ángulo de incidencia, puede ocurrir una
reflexión total del rayo al pasar del agua al aire? Justificarlo
a)
El rayo incidente se refracta en el agua sufre una reflexión especular
y después se vuelve a refractar al pasar del agua al aire.
Como el ángulo de incidencia del segundo cambio de medio (agua-
aire) es igual que el de refracción del primer cambio (aire-agua) por
lo tanto el ángulo de refracción que se observa cuando el rayo pasa
al aire es igual que el ángulo con que incidió pero medido hacia el
otro lado de la normal.
El resultado final es el mismo que si hubiera sufrido una reflexión
especular.
b) Analíticamente se puede ver sin necesidad de resolver la ec. de Snell.
Aire – agua → na sen 30 = naq sen r
Reflexión: → r = r’
Agua – aire → naq sen r’ = na sen α
Como r = r’ ⇒ naq sen r’ = na sen 30 ⇒ α = 30
c) La reflexión especular se produce para todos los ángulos de incidencia superiores al
ángulo límite, que es el ángulo para el que el ángulo de refracción es 90º.
naq sen i = na sen 90;
aq
a
n
n
isen =
Como na < naq habrá un ángulo i cuyo seno tome ese valor.
Solamente se puede observar el fenómeno de la reflexión total cuando pasamos de un medi
a otro con menor índice de refracción.

CUESTIÓN C
Si lo que queremos es que el rayo incida desde el aire al agua, se refleje en el fondo del
vaso y a la salida se produzca la reflexión total, el proceso no se puede producir ya que
como hemos visto en el apartado b) el proceso de entrada y salida del rayo es
geométricamente simétrico. De este modo, para que no salga al aire, no debería haber
entrado desde el aire.

OPCIÓN 2 / PROBLEMA 1
PROBLEMAS
OPCIÓN 2
2-1. Una masa de 20 g realiza un movimiento vibratorio armónico simple en el
extremo de un muelle que da dos oscilaciones, siendo la amplitud del mismo 5 cm.
Calcular:
a) 0,75 PUNTOS La velocidad máxima de la masa que oscila.
b) 0,75 PUNTOS La aceleración de la masa en el extremo del movimiento.
c) 0,5 PUNTOS La constante del muelle.
a) Escribimos en primer lugar la ecuación del movimiento:
tπ4cos05,0tωcosAx ==
La velocidad será:
tπ4sen05,0·π4v −=
Su valor máximo se obtiene cuando sen 4πt = -1
s/mπ2,0005,0·π4vmax ==
b) La ecuación de la aceleración es:
( ) ( ) x·π4tπ4cos05,0·π4a
22
−=−=
En el extremo del movimiento x = A de modo que sustituyendo se tiene:
( ) 22
s/m9,705,0·π4a =−=
c) La constante del muelle se obtiene a partir de la expresión de la frecuencia:
m/N16,302,0·2·π4mfπ4k
m
k
π2
1
f 2222
===⇒=

CANTABRIA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 2
B a) Escribe la ecuación de una onda armónica que se propaga en el sentido positivo del
eje X, sabiendo que su frecuencia es 5 · 1010
Hz; su velocidad de propagación, 15 m/s, y
su amplitud, 0,5 m. (1,25 puntos. )
b) ¿Cómo sería la ecuación si la misma onda se propagara en el sentido negativo del
eje X? (0,75 puntos.)
a) La ecuación general de una onda que se propaga en el sentido de las x positivas es:
· t··2-· x
·2
sen·Ay 





νπ
λ
π
=
La velocidad de propagación es: v = λ · ν;
Por tanto la longitud de onda es: m10·3
10·5
15
n
v 10-
10
===λ
Finalmente la ecuación queda: · t10·5··2-
10·3
· x·2
sen·0,5y 10
10






π
π
=
· t10··10-
10·3
· x·2
sen·0,5y 10
10






π
π
=
b) Para que se propague con sentido contrario hay que cambiar x por -x, o t por -t:
· t10··10
10·3
· x·2
sen·0,5y 10
10






π+
π
=

CANTABRIA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 5
2. Una masa m = 10-3
kg que describe un movimiento armónico simple (m.a.s.), tarda 1
s en desplazarse desde un extremo de la trayectoria a1 otro extremo. La distancia entre
ambos extremos es de 5 cm. Determina:
a) El periodo del movimiento. (0,5 puntos.)
b) La energía cinética de la partícula en t = 2,75 s, sabiendo que en t = 0 su elongación
era nula. (0,75 puntos.)
c) El primer instante en que las energías cinética y potencial del sistema coinciden.
(0,75 puntos.)
a) El periodo es el tiempo que tarda una oscilación entera y es: 2 s.
b) El movimiento es: x(t) = A · sen(
T
· t·2 π
+ φ) = 0,025 · sen (π · t)
donde se ha tenido en cuenta que φ = 0 para que x(0) = 0.
La velocidad será: v(t) = dx/dt = 0,025 · π · cos(π · t)
v(2,75) = 0,25 · π · cos(π · 2,75) = -5,6 · 10-2
m · s-1
La energía cinética es: EC = _ m · v2
= _ · 10-3
· (-0,56)2
= 1,55 · 10-6
J
c) La energía total del sistema es la equivalente a la energía cinética máxima. La energía cinética
máxima es: ECmax = _ m · vmax
2
= _ · 10-3
· (0,025 · π)2
= 3,08 · 10-6
J
La energía potencial tendrá el mismo valor que la cinética cuando el valor de la cinética sea la
mitad de la máxima: _ · m · (0,025 · π · cos(π · t))2
= _ 3,08 · 10-6
Por tanto, cos2
(π · t) = 0,5; por tanto, t = 0,25 s

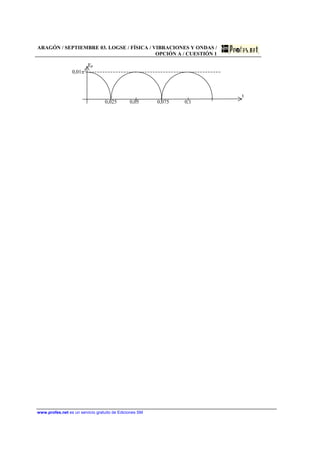
CANTABRIA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
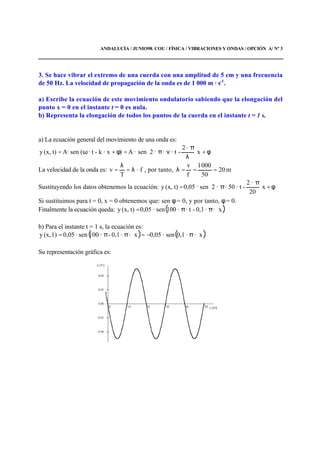
D. La ecuación de una onda transversal que se propaga por una cuerda viene; dada por
la expresión y = 0,25 sen [5 · (20 t - x)] en unidades del S.I.
a) ¿Qué quiere decir que esta onda es doblemente periódica?
b) ¿Qué valen, en este caso, los dos parámetros que caracterizan cada una de las dos
periodicidades?
a) La onda que se presenta es doblemente periódica ya que es periódica en el tiempo y en el
espacio, es decir, para un punto fijo del espacio la amplitud varía con el tiempo y para un
instante de tiempo determinado la amplitud varía con la posición.
b) La ecuación tras desarrollarla queda: y = 0,25 · sen(100 · t - 5 · x)
El factor que multiplica al tiempo t y caracteriza la periodicidad en el tiempo se denomina
frecuencia angular y su valor es: ω = 100 rad · s-1
. Por tanto la onda varía con el tiempo como
ω · t.
El factor que multiplica a la posición x y caracteriza la periodicidad en el espacio se denomina
número de onda y su valor es: k = 5 rad · m-1
. La variación de la onda con el espacio es k · x.

CANTABRIA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
CUESTIÓN B
En la primera de las dos gráficas que
se muestran en la página siguiente se
representa la variación con el tiempo
del desplazamiento (elongación que
experimenta una partícula que se
mueve con un movimiento armónico
simple (m.a.s.).
a) ¿Cuál de las curvas numeradas, en
la segunda gráfica, puede representar
la variación de la aceleración con el
tiempo del citado m.a.s.?
b) Representa gráficamente las
energías cinética, potencial y total del
anterior m.a.s. en función del tiempo
utilizando los mismos ejes para las tres
curvas.
Nota: las respuestas deben ser
razonadas.
a) La aceleración de un movimiento armónico es: · x
m
k
m
· xk
m
F
a −=
−
==
Por tanto la curva correcta es igual a la posición pero con el signo cambiado. Es la 4.
b) La energía potencial es E =
2
1
· k · x2
, mientras que la cinética es: E =
2
1
· m · v2
Sus representaciones gráficas, para los mismos intervalos de tiempo que en el apartado anterior
son:
3 421
AceleraciónElongación
Tiempo
Etotal
Ek
Ep

CANTABRIA / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS / CUESTIÓN 4
Discute brevemente cómo variarán, en un movimiento ondulatorio, cuando aumentamos
la frecuencia de la onda, las magnitudes siguientes:
a) Amplitud.
b) Periodo.
c) Velocidad de propagación.
d) Longitud de onda.
a) La amplitud de una onda es independiente de la frecuencia de la misma. Por tanto no variará.
b) El periodo es la inversa de la frecuencia, por tanto disminuirá.
c) La velocidad de propagación en la mayor parte de los medios no depende de la frecuencia de
la onda. Por tanto permanecerá constante.
d) La longitud de onda se describe como: λ = v · T, donde v es la velocidad de propagación de la
onda. Puesto que la velocidad no varía y el periodo disminuye, la longitud de onda disminuirá.

CANTABRIA / SEPTIEMBRE 2000. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ CUESTIÓN B
CUESTIÓN B
Dos partículas describen sendos movimientos armónicos simples (m.a.s.) de frecuencias
ν1 = 1 kHz y ν2 = 2 kHz y de la misma amplitud A = 1 cm.
a) ¿En qué instante de tiempo la partícula 2 tendrá la misma velocidad que la que tiene la
partícula 1 en t = 1 s?
b) ¿Cuál de los dos m.a.s. tendrá una mayor energía mecánica sabiendo que la masa de
ambas partículas es la misma, m1 = m2 = 10-3
kg?
a) Los movimientos serán: y1 = A cos(2πν1t); y2 = A cos(2πν1t)
Las velocidades son las derivadas y serán: v1 = -2πAν1 sen(2πν1t); v2 = -2πAν2 sen(2πν2t)
La velocidad de la partícula 1 en t = 1 s será: v1 = -2πAν1 sen(2π · 103
· 1) = 0
Un instante de tiempo en el que la primera partícula tendrá la misma velocidad que la segunda
será también para t = 1 s.
b) La energía de un m.a.s. es: E =
2
1
kA2
=
2
1
m ω2
A2
= 2π2
m ν2
A2
La partícula que tenga mayor frecuencia será la de mayor energía, la partícula 2.

CANTABRIA / SEPTIEMBRE 2000. SELECTIVIDAD / FÍSICA / VIBRAC. Y
ONDAS / CUESTIÓN D
CUESTIÓN D
a) Escribe la ecuación de una onda transversal que se propaga en una cuerda en la
dirección del eje Z. 0,25 puntos
b) ¿Qué diferencia existe entre la velocidad de propagación de la onda y la de vibración
de un punto de la cuerda? Deduce una expresión analítica para ambas velocidades. 0,75
puntos
a) y = A cos(k z – ω t)
b) La velocidad de propagación tiene que ver con la variación de la fase de la onda. Puesto que
una onda recorre una longitud de onda en la duración de un periodo se tiene que la velocidad de
propagación de la onda será: νλ=
λ
=
T
v
Por el contrario la velocidad de cada punto de la cuerda depende de la amplitud de la onda, y la
velocidad es la derivada temporal del vector posición: vy =
dt
dy
= A ω sen(k z – ω t)

CUESTIONES
C
a) El sonido ¿es una onda longitudinal o transversal? Explica cómo se propaga.
b) ¿Pueden una onda longitudinal y una transversal tener la misma velocidad de
propagación en el mismo medio material? Dar un ejemplo de cada tipo de onda.
a) Las ondas sonoras se producen como consecuencia de una compresión del medio a lo largo de
la dirección de propagación, son, por tanto, ondas longitudinales.
Se puede explicar la propagación de las ondas sonoras viendo el símil con las ondas que se
propagan a lo largo de un muelle como consecuencia de una compresión longitudinal del mismo.
b) No, porque la velocidad de propagación depende de las características del medio de
propagación, y un medio no tiene las mismas características en todas las direcciones.
Un ejemplo de onda transversal, es la onda que se produce cuando se lanza una piedra a un río.
Por otro lado, una onda longitudinal sería la producida al comprimir un muelle.

OPCIÓN DE PROBLEMAS Nº 2
1-2 Una onda transversal se propaga en un medio material según la ecuación:
y(x,t) = 0,2· sen(2ππ (50t-x/0,10)), en unidades del SI.
a) Determinar la amplitud, período y longitud de onda.
b) Calcular la velocidad de propagación de la onda.¿En qué sentido se propaga?
c) ¿Cuál es la máxima velocidad de vibración de las partículas en el medio?
d) Calcular la diferencia de fase, en un cierto instante t, entre dos puntos que distan
entre sí 2,5 cm.
a) La ecuación general de una onda es la siguiente:
)kxft(2sen·A)t,x(y ±π=
Identificando los parámetros de la ecuación del enunciado:
Amplitud: A = 0,2
Período: 0,02sT ===
50
1
f
1
Longitud de onda: 10më ===
1,0
1
k
1
b) La velocidad de propagación se calcula según la fórmula:
500m/sv =⋅=λ=
λ
= 5010f·
T
Laonda se propaga en el sentido negativo del eje x debido al signo negativo de la ecuación.
c) Para calcular la velocidad de vibración se deriva la ecuación de la onda:
62,83m/s=π=⇒−ππ=
∂
∂
= 50·2·2,0V)1,0/xt50(2)·cos50·2·(2,0
t
y
V max
d)
)
1,0
x
t50(2sen·2,0y
)
1,0
x
t50(2sen·2,0y
2
2
1
1
−π=
−π=
m
2
ð
=−
π
=−π−−π=δ⇒ )xx(
1,0
2
)
1,0
x
t50(2)
1,0
x
t50(2 21
21

CANTABRIA / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
PRIMERA PARTE
CUESTIÓN A
A. Para una masa m realizando oscilaciones armónicas de amplitud A y pulsación ω,
alrededor del punto x = 0,
a) 1 PUNTO Calcular la relación entre la energía cinética y la potencial en x = A/3.
b) 1 PUNTO ¿En qué puntos de la trayectoria es máxima la energía potencial?
a) Las expresiones de ambas energías son:
tωsenAωm
2
1
mv
2
1
E
tωcoskA
2
1
kx
2
1
E
2222
c
222
p
==
==
Calculamos el valor del seno:
9
8
9
1
1tωsen1tωcostωsen
3
1
tωcostωcosA
3
A
;
3
A
x
222
=−=⇒=+
=⇒==
Sustituyendo:
pc
22
22
p
c
E8E8
9
1
Aωm
2
1
9
8
Aωm
2
1
E
E
=⇒==
b) El valor de la x se hace máxima en los extremos de la trayectoria que coincide con la
amplitud x = A, luego la energía potencial será:
2
max,p kA
2
1
E =

CANTABRIA / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
PROBLEMAS
OPCIÓN 1
1-1. La Luna tiene una masa que es 0,0123 veces la de la Tierra y su radio es cuatro
veces menor. Calcular:
a) 1 PUNTO La longitud del péndulo que bate segundos en la Luna (péndulo de periodo
1 segundo)
b) 1 PUNTO El ahorro de energía, respecto de la necesaria en la Tierra, al levantar un
cuerpo de masa 1000 kg a una altura de 10 metros sobre el nivel del suelo.
Datos: g = 9,8 m/s2
.
a) El periodo de un péndulo depende del valor del campo gravitatorio, g. Como conocemos
el valor del campo en la Tierra, intentaremos escribir el de la Luna en función de este.
2
L
2
T
T
2
T
T
2
L
L
L2
T
T
s/m9286,18,9·0123,0·16g
R
M
G·0123,0·16
16
R
M0123,0
G
r
m
Gg;
R
M
Gg
==
====
Conocido el valor del campo, despejamos de la expresión del periodo del péndulo el valor
de la longitud.
m05,0
π4
1·9286,1
π4
Tg
L
g
L
π2T 22
2
L
L
===⇒=
b) El trabajo realizado por las fuerzas del campo en las proximidades de la superficie se
puede expresar como:
( ) J9800010·8,9·1000hhmgEEE∆T f0pf0pP −=−=−=−=−=
Que el trabajo sea negativo quiere decir que se realiza en contra de las fuerzas del campo
ya que lo que se ha hecho es aumentar la energía del cuerpo. Es decir vamos a considerar
que hemos ejercido98000 J.
En la Luna será:
J1928610·9286,1·1000h∆mgT −==−=
La diferencia entre ambas energías es: 98000 – 19286 = 78724 J
Es decir que tenemos que nos ahorramos78724 J si estamos en la Luna.

CANTABRIA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 2
B. La elongación de una partícula de masa m = 1 kg que describe un movimiento
armónico simple viene determinada por la ecuación siguiente: y = 0,3 · sen(12 · · t)
m.
a) ¿En qué primer instante de tiempo la energía cinética y potencial de la partícula son
iguales? (1 punto)
b) ¿Qué vale la energía mecánica total de este oscilador? (1 punto)
a) La energía potencial del oscilador es proporcional al cuadrado del desplazamiento:
2
Pmax A·k·
2
1
E =
Por tanto para que la energía potencial sea igual que la cinética implica que la energía potencial
del oscilador es la mitad de la energía total del sistema, por tanto:
· t)·(12sen·A·k·
2
1
A·k·
4
1
2
E
E 222Pmax
P π===
Por tanto: 5,0)· t·21(sen 2
=π
Despejando se obtiene que: s021,0)5,0arcsen(·
·12
1
t =
π
=
b) La velocidad de este oscilador es la derivada de la posición con el tiempo, es decir:
v = 12 · 0,3 · cos(12 · π · t) = 3,6 · cos(12 · π · t) m · s-1
Por tanto la energía cinética máxima es: J48,63,6·1·
2
1
· vm·
2
1
E 2
max
2
Cmax ===

CATALUÑA / JUNIO 04. LOGSE-SERIE 3/ FÍSICA / VIBRACIONES Y
ONDAS/ PRIMERA PARTE / CUESTIÓN 2
CUESTIÓN 2
C2. Calcule el valor de la longitud de onda asociada a un fotón de energía 3 keV.
Datos: h = 6,62 · 10–34
J · s, c = 3 · 108
m/s, 1 eV = 1,609 · 10–19
J.
A partir de la energía calculamos el valor de la frecuencia. En primer lugar pasamos la energía a
unidades del sistema internacional.
J10·07,510·69,1·10·3keV3E 16193 −−
===
Hz10·66,7
10·62,6
10·07,5
h
E
ννhE 17
34
16
===⇒= −
−
La velocidad del fotón es la de la luz:
m10·92,3
10·66,7
10·3
ν
c
λcλν 10
17
8
−
===⇒=

CATALUÑA / SEPTIEMBRE 04. LOGSE-SERIE 5/ FÍSICA / VIBRACIONES
Y ONDAS / SEGUNDA PARTE / OPCIÓN B / CUESTIÓN 3
SEGUNDA PARTE OPCIÓN B
C-3. Un tren de ondas atraviesa un punto de observación. En este punto, el tiempo
transcurrido entre dos crestas consecutivas es de 0,2 s. De las afirmaciones siguientes,
escoja la que sea correcta y justifique la respuesta.
a) La longitud de onda es de 5 m.
b) La frecuencia es de 5 Hz.
c) El período es de 0,4 s.
d) Ninguna de las afirmaciones anteriores es correcta.
El tiempo que tardan en pasar 2 crestas consecutivas es lo que conocemos como periodo.
T = 0,2 s.
Los únicos apartados que están relacionados con el periodo son el b) y el c) luego el a) no
puede ser válido.
Como el c) indica directamente que el periodo es 0,4 s es falso. El apartado b) hace
referencia a la frecuencia, que es la magnitud inversa del periodo. Calculamos su valor:
Hz5
2,0
1
T
1
f ===
El apartado b) es el correcto.

Y ONDAS / OPCIÓN B / ACTIVIDAD 2
OPCIÓN B
C-2. La posición de una partícula puntual de masa 500 g que describe un
movimiento vibratorio armónico viene dada en unidades del SI por x = 0,30 sen
(20πt). Calcula:
a) La energía cinética máxima de la partícula
b) La fuerza máxima que actúa sobre ella.
RESPUESTA:
a) Calculamos las expresiones de la velocidad y de la aceleración del movimiento.
( ) ( )t20sen120
dt
dv
a;t20cos6
dt
dx
v 2
ππππ −====
La energía cinética máxima se da para la velocidad máxima, es decir cuando el coseno vale
la unidad:
( )( ) J8,8865,0
2
1
E;mv
2
1
E max,c
2
maxmax,c === π
b) La fuerza máxima se produce cuando la aceleración de la partícula es máxima:
( )( ) N2,5921205,0F;a·mF 2
maxmaxmax === π

CATALUÑA / JUNIO 03. LOGSE-SERIE 5/ FÍSICA / VIBRACIONES Y ONDAS /
PRIMERA PARTE / CUESTIÓN 2
PRIMERA PARTE
C2. La ecuación de una onda transversal, en unidades del SI, es y = 0,04 sin 2π (t/2 - x/4).
Determine el periodo la longitud de onda, la frecuencia y la velocidad de propagación.
La ecuación de la onda es:






λ
−π=
x
T
t
2Aseny
Comparando con la ecuación dada se tiene:
T = 2 s; Hz5,0
T
1
==υ
s/m2v;m4 =λυ==λ

CATALUÑA / JUNIO 98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 5
3. La frecuencia del sonido que emite la sirena de una ambulancia es f0. Si cuando la
ambulancia se aleja de un observador en reposo la frecuencia que detecta el observador
es f, razona cuál de las siguientes relaciones es cierta:
a) f < f0
b) f = f0
c) f > f0
La correcta es la a), f < f0 debido al llamado efecto Doppler.
Cuando la fuente sonora se aleja del observador la longitud de onda aumenta debido a que a la
velocidad con que se alejan las ondas de la ambulancia por su propia velocidad de propagación,
hay que sumar la velocidad del vehículo. Por tanto la longitud de onda del sonido emitido es
mayor que la longitud de onda natural en parado. Finalmente, puesto que la frecuencia es la
inversa de la longitud de onda, la frecuencia del sonido emitido al alejarse la ambulancia será
menor que el que se percibe cuando la ambulancia está parada.

Y ONDAS / PRIMERA PARTE / CUESTIÓN 1
PRIMERA PARTE
Q1. Una partícula de masa 500 g describe un movimiento vibratorio armónico de
manera que su posición (en unidades del sistema internacional) esta dada por x = 0,20
sen (10π t), donde t es el tiempo. Calcula la energía cinética máxima de la partícula y
la fuerza máxima que actúa sobre ella. Indica en que puntos de la oscilación se
adquieren estos valores máximos.
Para calcular la energía cinética y la fuerza hay que conocer previamente las expresiones de
la velocidad y de la aceleración del movimiento vibratorio, por tanto derivamos en la
ecuación del movimiento para obtenerlas:
)tπ10(senπ20
dt
xd
a);tπ10cos(π2
dt
dx
v 2
2
2
−====
Sustituyendo en la fórmula de a energía cinética:
)tπ10(cosπ4·5,0·
2
1
mv
2
1
E 222
c ==
El valor máximo se da cuando la velocidad alcanza su valor máximo en el punto medio de
la oscilación.
J87,9π4·5,0·
2
1
mv
2
1
E 22
maxmax,c ===
De igual modo el valor de la fuerza es:
)tπ10(senπ20·5,0amF 2
−==
Su valor máximo se obtiene para el valor máximo de su aceleración en los extremos de la
trayectoria:
N7,98π20·5,0amF 2
maxmax =−==

EXTREMADURA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
4. Escribe la ecuación de una onda que se propaga en el sentido positivo del eje X y que
tiene las siguientes características: 0,5 Hz de frecuencia, 100 m/s de velocidad y 0,2 m
de amplitud.
La ecuación general de una onda que se propaga en el sentido de las X positivas es:






φ+νπ
λ
π
=φ+ω= · t··2-
· x·2
sen·A)· t-· xsen(k·Ay
Para obtener la ecuación de onda hay que determinar la longitud de onda haciendo uso de la
velocidad de propagación de la onda:
νλ=
λ
= ·
T
v ; por tanto, m200
0,5
100v
==
ν
=λ
Sustituyendo los parámetros obtenidos en la ecuación general se obtiene la ecuación de la onda:
( )· t-· x·0,01sen·0,5· t0,5··2-
200
· x·2
sen·0,5y ππ=





π
π
=

EXTREMADURA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 5
5. La onda estacionarla y = 0,04 · cos ( · x) · sen ( · t) ha sido obtenida por la
superposición de dos ondas armónicas.
a) Explica en qué condiciones se ha debido dar la superposición y escribe las
ecuaciones de las dos ondas superpuestas.
b) ¿Qué distancia se dará entre dos nodos sucesivos de la onda estacionaria propuesta?
a) Una onda estacionaria es el resultado de la interferencia entre dos ondas armónicas de igual
amplitud y frecuencia que se propagan con la misma dirección y sentido contrario.
La ecuación del enunciado se puede separar en dos partes utilizando las relaciones
trigonométricas, obteniéndose el siguiente resultado:
y = 0,04 · cos (π · x) · sen (π · t) = 0,02 · sen(π · x + π · t) - 0,02 sen(π · x - π · t)
Por tanto las ecuaciones de las ondas iniciales son:
y1 = 0,02 · sen(π · x + π · t)
y2 = -0,02 sen(π · x - π · t) = 0,02 sen(π · x - π · t + π)
b) La distancia entre dos nodos se define como el semiperiodo de la onda y se determina a
partir de la periodicidad espacial: cos (π · x)
cos (π · x) = 0 implica x = (n + _) con n = 1, 2, 3, ...
Por tanto la distancia entre dos nodos es: d = xi+1 - xi = (i + 1 + _) - (i + _) = 1 m

GALICIA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
PROBLEMA 1
1. Un resorte de masa despreciable se estira 0,1 m cuando se la aplica una fuerza de
2,45 N. Se fija en su extremo libre una masa de 0,085 kg y se estira 0,15 m a lo largo
de una mesa horizontal desde su posición de equilibrio y se suelta dejándolo oscilar
libremente sin rozamiento. Calcula: a) la constante elástica del resorte y su periodo de
oscilación; b) la energía total asociada a la oscilación y las energías potencial y
cinética cuando x = 0,075 m
a) A partir del estiramiento que produce la fuerza de 2,45 N calculamos el valor de la
constante K aplicando la ley de Hooke.
m/N5,24
1,0
45,2
x
F
Kx·KF ==
−
=⇒−=
Para calcular el periodo de oscilación, hallamos en primer lugar el valor de la frecuencia y
despejamos a partir de el. Aplicando el principio fundamental de la dinámica al las
ecuaciones del movimiento vibratorio se tiene:
x·ω·ma·mF 2
−==
Igualando esta expresión a la de la ley de Hooke:
22
ωmKx·ω·mx·K =⇒−=−
Despejamos la frecuencia angular:
s37,0
5,24
085,0
π2
K
m
π2
ω
π2
T;
m
K
ω =====
b) Expresamos la energía total como suma de la cinética y la potencial elástica.
( ) ( ) 22222222
T
22
PCT
ωmA
2
1
tωcosωmA
2
1
tωsenωmA
2
1
E
tωsen·ωAv
tω·cosAx
Kx
2
1
mv
2
1
EEE
=+=
⎭
⎬
⎫
−=
=
+=+=
Sustituyendo los valores que tenemos:
J8375,115,0·
085,0
5,24
·085,0·
2
1
ET ==
Para la posición x = 0,075 m, la energía potencial vale:
( ) J0689,0075,0·5,24·
2
1
Kx
2
1
E 22
P ===
El valor de la energía cinética lo calculamos restando este valor al total de la energía.

J7686,10689,08375,1EEE PTC =−=−=

GALICIA / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A /
ACTIVIDAD 2
OPCIÓN A
CUESTIÓN 2
2. En una onda estacionaria generada por interferencia de dos ondas, se
cumple: a) La amplitud es constante, b) la onda transporta energía, c) La
frecuencia es la misma que las de las dos ondas que interfieren.
RESPUESTA:
El apartado a) no es correcto porque la amplitud depende del punto de la onda en que
nos encontremos.
El apartado b) tampoco es correcto porque las ondas estacionarias se caracterizan
porque no transportan energía.
El apartado c) si es correcto porque para que se produzca una onda estacionaria
tienen que interferir dos ondas de igual amplitud y frecuencia con un desfase
determinado.

GALICIA / SEPTIEMBRE 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN
A / ACTIVIDAD 1
OPCIÓN A:
PROBLEMA 1
1. Una onda periódica viene dada por la ecuación y (t,x) = 10 sen 2π (50t –
0,20x) en unidades del S.I. Calcula: a) la frecuencia, la velocidad de fase y la
longitud de onda; b) la velocidad máxima de una partícula del medio, y los
valores del tiempo t para los que esa velocidad es máxima (en un punto que
dista 50 cm del origen)
RESPUESTA:
a) Comparamos la ecuación dada con la ecuación general de un movimiento
ondulatorio:
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
λ
x
T
t
π2senA)kxtω(senA)t,x(y
s/m250λυ
T
λ
v
m5
2,0
1
λ2,0
λ
1
Hz50
T
1
υ
f ===
==⇒=
==
b) Derivamos la ecuación de la posición:
( )x2,0t50π2cos10·50·π2
td
)t,x(yd
)t,x(v −==
El valor máximo de la velocidad se produce cuando el coseno vale la unidad.
s/mπ100010·50·π2vmax ==
Para un punto que dista 50 cm del origen esto se produce cuando el tiempo vale:
( )
s022,0
50
1,1
t
)1n(11,0t50
...2,1,0n;πn25,0·2,0t50π2
==
==−
±±==−

GALICIA / SEPTIEMBRE 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN
A / ACTIVIDAD PRÁCTICA
OPCIÓN A
CUESTIÓN PRÁCTICA
La constante elástica de un resorte medida por el método estático: a)
¿depende del tipo de material?, b) ¿varia con el periodo de oscilación?, c)
¿depende de la masa y la longitud del resorte?
RESPUESTA:
Cuando se mide la constante elástica por el método estático se obtienen la ley de
Hooke en la que las elongaciones del muelle son proporcionales a las fuerzas
realizadas sobre el mismo.
k
L∆
F
;L∆kF ==
De este modo el valor de la constante del muelle depende del tipo de material y de las
características de su fabricación.
Al estar utilizando el método estático no podemos decir nada acerca de la influencia
del periodo d las oscilaciones ya que al muelle no se le somete a oscilaciones.
La masa del resorte no influye en el valor de su constante. Tampoco el valor de su
longitud, aunque si la diferencia entre su longitud natural L0 y las diferentes
longitudes que tome el mismo al verse sometido a distintas fuerzas.

GALICIA / JUNIO 2000. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN
1 / CUESTIÓN TEÓRICA 3
OPCIÓN 1
CUESTIÓN TEÓRICA 3
¿Cuál de las expresiones propuestas representa una onda transversal que se propaga en
el sentido positivo del eje x con una velocidad de 5 m/s, tiene una amplitud de 1 m y una
frecuencia de 10 Hz?: a) y = cos 2π(10t - 5x), b) y = cos 4π(5t - x)
En una onda, el factor que multiplica al tiempo es 2 π f. Por tanto en el caso a) la frecuencia es de
10 Hz. En el caso b) la frecuencia es el doble.

OPCIÓN 1 / CUESTIÓN 2
OPCIÓN 1
CUESTIÓN 2
La energía de una onda es proporcional:
a) Al cuadrado de la amplitud
b) A la inversa de la frecuencia
c) A la longitud de onda
La energía de una partícula afectada por un movimiento ondulatorio es:
( ) ( )[ ] 22
0
2
0
222
pc Aωm
2
1
φtωsenφtωcosAωm
2
1
EEE =+++=+=
Luego la respuesta correcta es la a), la energía de la onda depende del cuadrado de la
amplitud.

GALICIA / JUNIO98. LOGSE / FÍSICA / VIBRACIOENS Y ONDAS / OPCIÓN A/ Nº 2
2. Un péndulo simple oscila con una elongación máxima de 18º, desarrollando 10
oscilaciones por segundo.
Tomando como instante inicial la posición de equilibrio:
a) Escribe su elongación en función del tiempo.
b) Determina su periodo de oscilación en la Luna, donde la gravedad es,
aproximadamente, un sexto de la terrestre.
a) La ecuación general, expresada en grados, del movimiento es:
φ = φ0 · cos(ω · t) = φ0 · cos(2 · π · ν · t) = 18 · cos(2 · π · 10 · t) = 18 · cos(20 · π · t)
b) El periodo de oscilación de un péndulo simple es:
g
l
T =
Si la gravedad varía la frecuencia también lo hará:
g'
l
T'=
Por tanto, si dividimos las dos igualdades:
g'
g
T
T'
=
Despejando y sustituyendo se obtiene el valor del periodo de oscilación en la Luna:
s0,256·0,1
6
g
g
·
10
1
g'
g
·
1
g'
g
·T'T ===
ν
==

GALICIA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN 1 /
PROBLEMA 2
Una masa de 0,05 kg realiza un m.a.s. según la ecuación:
x = A · cos (ω · t + ϕ)
Sus velocidades son 1 y 2 m/s cuando sus elongaciones son, respectivamente, 0,04 y 0,02
metros.
Calcula:
a) El periodo y la amplitud del movimiento.
b)La energía del movimiento oscilatorio y las energías cinética y potencial cuando x =
0,03 m.
a) La velocidad de un movimiento armónico es: v = A · ω · sen(ω · t + ϕ)
Puesto que es un movimiento oscilatorio se puede ver que:
2
2
2
2
A
v
x =
ω
+
Si dividimos las dos situaciones entre sí tenemos:
1-
22
22
2
1
2
2
2
2
2
1
2
2
22
2
2
2
12
1
s·rad50
04,002,0
21
xx
vv
v
x
v
x
1 =
−
−
=
−
−
=ω⇒
ω
+
ω
+
=
Finalmente el periodo es: s126,0
50
·2·2
T =
π
=
ω
π
=
La amplitud del movimiento se calcula con la primera ecuación:
m045,0
50
1
04,0
v
xA 2
2
2
2
2
2
=+=
ω
+=
b) Las distintas energías de un movimiento armónico son:
Ep =
2
1
· k · x2
=
2
1
· m · ω2
· x2
=
2
1
· 0,05 · 502
· 0,032
= 5,6 · 10-2
J
La energía total es: E =
2
1
· k · A2
=
2
1
· m · ω2
· A2
=
2
1
· 0,05 · 502
· 0,0452
= 0,127 J
La energía cinética será la resta de ambas: Ek = E - Ep = 0,127 - 0,056 = 7,1 · 10-2
J

OPCIÓN 2
CUESTIÓN 2
De la hipótesis de De Broglie, dualidad onda-corpúsculo, se deriva como
consecuencia: a) Que los electrones pueden mostrar comportamiento ondulatorio λ =
h/p
b) Que la energía de las partículas atómicas está cuantizada E = hν
c) Que la energía total de una partícula E = mc2
.
La hipótesis de De-Broglie plantea que al igual que la luz presenta propiedades
corpusculares y ondulatorias, podrá darse la situación recíproca es decir que un ente
corpuscular como cualquier partícula material podría presentar propiedades ondulatorias.
Descubre que en efecto esta situación se da, pero el orden de magnitud de las características
ondulatorias es tan pequeño que prácticamente no se pueden percibir salvo en casos de
partículas atómicas.
La respuesta correcta es que el electrón puede presentar comportamiento ondulatorio
p
h
λ =
que es la opción a).

OPCIÓN 2
CUESTIÓN 3
En un péndulo simple, indica cual de las siguientes graficas se ajusta correctamente
con la relación energía/elongación:
En un péndulo simple la energía potencial es máxima en los extremos de la trayectoria y
nula en el centro de la misma, luego la grafica a) es incorrecta.
La energía cinética es máxima en el punto de equilibrio y mínima en los extremos, luego la
gráfica de la opción b) también es incorrecta.
La respuesta correcta es la c) ya que presenta una gráfica de la energía total que en todo
momento se conserva ya que es constante su valor.

GALICIA / SEPTIEMBRE 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN 1 / CUESTIÓN 2
CUESTIÓN 2
2. Si un oscilador armónico se encuentra en un instante dado en una posición x que es
igual a la mitad de su amplitud (x = A/2) la relación entre la energía cinética y la
potencial es: a) EC = EP ; b) EC = 2EP ; c) EC = 3EP
Las expresiones de las energías cinética, potencial y total para un oscilador armónico son:
22
T
2
c
2
p
Aωm
2
1
E
mv
2
1
E
kx
2
1
E
=
⎪
⎪
⎭
⎪⎪
⎬
⎫
=
=
Si x = A/2 Los valores de las energías son:
4
A3
ωm
2
1
4
A
ωm
2
1
Aωm
2
1
EEEE
4
A
ωm
2
1
E
2
2
2
222
TPTC
2
2
P
=−==−=
=
La relación entre ambas energías es:
pc
22
22
p
c
E3E3
4
1
Aωm
2
1
4
3
Aωm
2
1
E
E
=⇒==
La respuesta correcta es la c).

GALICIA / SEPTIEMBRE 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN 1 / CUESTIÓN PRÁCTICA
CUESTIÓN PRÁCTICA
En el estudio estático de un resorte se representan variaciones de longitud (∆li) frente
a las fuerzas aplicadas (Fi), obteniendo una línea recta. En el estudio dinámico del
mismo resorte se representan las masas (mi) frente a los cuadrados de los periodos
(Ti
2
), obteniéndose también una recta. ¿Tienen las dos la misma pendiente? Razona la
respuesta.
En el estudio estático de un resorte, cuando se cuelgan diferentes masas del mismo, la
fuerza con la que reacciona el muelle según la ley de Hooke es proporcional al estiramiento
del muelle y esa proporcionalidad viene dada por la constante del muelle.
k
x
F
;kxF −=−=
Como las fuerzas que realizamos son del mismo valor y sentido contrario a las del muelle,
podemos escribir:
k
x
F
i
i
=
La representación gráfica de estos datos es una recta cuya pendiente es k.
Cuando realizamos el estudio dinámico, nos encontramos con que la relación entre la masa
y el periodo del resorte es:
x·ω·mF;xωa;a·mF 22
−=−==
Igualando esta expresión a la de la ley de Hooke:
22
ω·mk;x·ω·mx·k;x·kF =−=−−=
Escribimos la frecuencia angular en función del periodo:
222
2
π4
k
T
m
T
π4
mk =⇒=

CASTILLA LA MANCHA / SEPTIEMBRE 04. LOGSE / FÍSICA /
VIBRACIONES Y ONDAS / OPCIÓN B / CUESTIÓN 1
OPCIÓN B
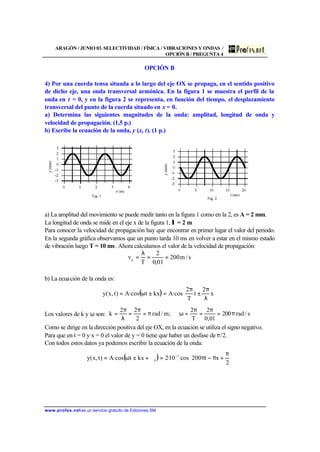
1.- La ecuación de una onda estacionaria en una cuerda, expresada en unidades del
S.I., es:
y(x,t)=0,2sen(πx)cos(40πt)
determina:
a) La velocidad de propagación de las ondas cuya superposición da lugar a esa
vibración.
b) La distancia entre un nodo y un vientre consecutivo.
c) Velocidad de un partícula de la cuerda situada en x = 1,5cm en el instante t =
1,125s.
d) La aceleración máxima de dicha partícula en cualquier instante.
a) Comparamos la ecuación del enunciado con la ecuación general de las ondas
estacionarias para poder reconocer las magnitudes que describen dicho movimiento
ondulatorio.
( ) ( ) ( )
s
20
1
40
2
Tπ40
T
π2
;m2λπ
λ
π2
tωcoskxAsen2t,xy
==⇒==⇒=
=
El valor de la velocidad de las ondas que se superpusieron es:
s/m40
20
1
2
T
λ
vp ===
b) La distancia entre dos nodos o dos vientres consecutivos en una onda estacionaria es la
mitad de la longitud de onda. De modo que si lo que queremos saber es la distancia entre
un nodo y un vientre consecutivos tendremos que dividir la longitud de onda entre cuatro.
m5,0
4
2
4
λ
d v,n ===
vientres
dn,v
nodos
c) Derivando la ecuación de la onda estacionaria obtenemos la velocidad de los puntos que
vibran en cada posición.
( ) ( ) ( )[ ] π40·tπ40senxπsen·2,0t,xv −=
Sustituyendo los valores dados:
( ) ( ) s/m0π40
8
9
senπ10·5,1sen·π40·2,0125,1;10·5,1v 22
=⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−= −−

VIBRACIONES Y ONDAS / OPCIÓN B / CUESTIÓN 1
La velocidad es cero cuando se trata de un nodo o cuando el punto que estamos estudiando
se encuentra en uno de los extremos de la vibración.
d) Derivamos de nuevo y sustituimos el valor dado para la posición pero dejamos sin
sustituir el tiempo:
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) 2222
2
s/mtπ40·cos8,148tπ40cosπ10·5,1senπ40·2,0t,10·5,1a
tπ40cosxπsenπ40·2,0
dt
t,xdv
t,xa
=−=
−==
−−

CASTILLA LA MANCHA / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN A / ACTIVIDAD 2
OPCIÓN A
2.- La ecuación de una onda plana viene dada por la expresión
y(x,t)=0’05sen(600πt-6πx+π/6)
en unidades del S.I. Hallar:
a) La amplitud, la frecuencia, la longitud de onda y la velocidad de
propagación
b) La velocidad máxima de vibración
c) La distancia entre dos puntos cuya diferencia de fase sea π/4
(3 puntos)
RESPUESTA:
a) Comparándola ecuación dada con la ecuación general de una onda:
( )0φkxtωsenA)t,x(y +−=
Tenemos:
A = 0,05 m
m
3
1
π6
π2
k
π2
λ
λ
π2
k ===⇒=
Hz300
π2
π600
π2
ω
ffπ2ω ===⇒=
s/m100300·
3
1
fλ
T
λ
vp ====
b) Derivamos la expresión de la posición para obtener la de la velocidad.
⎟
⎠
⎞
⎜
⎝
⎛
+−==
6
π
xπ6tπ600cos05,0·π600
dt
)t,x(yd
)t,x(v
El valor máximo lo obtenemos cuando el coseno vale la unidad
s/mπ3005,0·π600vmax ==
c) Restamos las fases denominando x1 y x2 a dichos puntos:
⎟
⎠
⎞
⎜
⎝
⎛
+−
6
π
xπ6tπ600 1 - ⎟
⎠
⎞
⎜
⎝
⎛
+−
6
π
xπ6tπ600 2 =
4
π
( ) m
24
1
xx;
4
π
xxπ6 1212 =−=−

VIBRACIONES Y ONDAS / OPCIÓN B / PROBLEMA 2
OPCIÓN B
PROBLEMAS
2.- Una onda armónica transversal se propaga hacia la derecha con una velocidad de
propagación de 600m/s, una longitud de onda de 6 m y una amplitud de 2 m. En el
instante inicial (t=0 s) y en el origen la elongación de la onda es nula.
a) Escribe la ecuación de la onda
b) Calcula la velocidad máxima de vibración
c) Calcula el tiempo necesario para que un punto a 12 m del origen alcance por
primera vez la velocidad máxima de vibración.
RESPUESTA:
a) Calculamos las magnitudes que intervienen en la ecuación de la onda a partir de los datos del
enunciado.
( )
s/rad200
T
2
s01,0
v
T
T
v
m/rad
3
2
k
kxtsenA)t,x(y
π
π
ω
λλ
π
λ
π
ω
==
==⇒=
==
−=
A partir de las condiciones iniciales calculamos el valor del desfase.
⎟
⎠
⎞
⎜
⎝
⎛
−=
=⇒==
x
3
t200sen2)t,x(y
00sen·2)0,0(y 00
π
π
φφ
b) Calculamos la expresión de la velocidad de vibración
⎟
⎠
⎞
⎜
⎝
⎛
−== x
3
t200cos200·2
dt
)t,x(dy
)t,x(v
π
ππ
La velocidad máxima se da cuando el coseno vale la unidad. π400vmax =

VIBRACIONES Y ONDAS / OPCIÓN B / PROBLEMA 2
c) La velocidad máxima la alcanza un punto del medio por primera vez cuando, una vez iniciado el
movimiento de vibración, pasa por la posición de equilibrio por primera vez. Esto quiere decir que
una vez que la vibración alcanza al punto debe transcurrir medio periodo.
Entonces el tiempo total que tiene que transcurrir es el que tarda la vibración en llegar al punto
más la mitad del periodo.
s025,0
600
15
2
01,0
600
12
2
T
v
x
2
T
tt 12xmax,v ==+=+=+= =

CASTILLA LA MANCHA / JUNIO 01. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
Una onda se propaga en el sentido negativo del eje X, siendo 20 cm su longitud de onda.
El foco emisor vibra con una frecuencia de 25 Hz, una amplitud de 3 cm y fase inicial
nula.
Determina:
a) La velocidad con que se propaga la onda.
b) La ecuación de la onda.
c) El instante en que un punto que se encuentra a 2,5 cm del origen alcanza, por primera
vez, una velocidad nula.
a) La velocidad de propagación está relacionada con la longitud de onda y la frecuencia a través
de la ecuación: v = λ ν
v = 0,2 · 25 = 5 m/s
b) La ecuación de la onda será:
)5010cos(03,02
2
cos)cos( txtxAtkxAy πππν
λ
π
ω −=





−=−=
c) La velocidad es la derivada con respecto al tiempo del desplazamiento. Por tanto será:
s10·5
50
25,0
050025,0·10
0)50025,0·10sen(71,4)5010sen(03,0·50
3-
==⇒=−
=−=−−=
π
π
ππ
πππππ
tt
ttxv

CASTILLA-LA MANCHA / JUNIO 02. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
www.profes.net es un servicio gratuito de Ediciones S M
OPCIÓN A
CUESTIÓN 4
En un partido de fútbol un espectador canta un gol con una sonoridad de 40 dB. ¿Cuál
será la sonoridad si gritaran a la vez y con la misma intensidad sonora los 1000
espectadores que se encuentran viendo el partido?
I0 = 10-12
W· m-2
Cuando grita una persona:
db40
Io
I
·log10 ==β
Si gritan 1000 personas a la vez:
dB70=β+=+⋅==β 30
Io
I
·log101000log10
Io
I·1000
·log102

ONDAS / OPCIÓN B
Problema 2
2.- La ecuación de una onda armónica que se propaga en una cuerda es:
y (x, t) = 0,5 sen (0,1πt – πx – π/3)
expresada en el S.I. de unidades. Determinar:
a) La amplitud, el periodo, la longitud de onda y la frecuencia angular
b) La velocidad de propagación
c) La velocidad transversal de un punto de la cuerda situado en x = 2 m en el
instante t = 10 s
Comparamos la onda dada con la ecuación general de una onda:
( )0φkxtωsenA)t,x(y;
3
π
xπtπ1,0sen·5,0)t,x(y +−=





−−=
a) m0,5A =
s20
π1,0
π2
ω
π2
T ===
m2
π
π2
k
π2
λ ===
s/radπ1,0ω =
b) La velocidad de la onda es:
s/m1,0
20
2
T
λ
v ===
c) Derivando la ecuación de la posición con respecto al tiempo se obtiene la ecuación de la
velocidad de vibración de las partículas de la cuerda.






−−==
3
π
xπtπ1,0cos5,0·π1,0
dt
)t,x(dy
)t,x(v
Sustituyendo x = 2 m; t = 10 s
s/m10·25,1
3
π2
·cos10·5,2
3
π
π210·π1,0cos10·5,2)t,x(v 333 −−−
−=




 −
=





−−=

CUESTIÓN 1
1.- Una onda armónica de frecuencia 100 Hz y 0’5 m de amplitud se propaga con una
velocidad de 10m/s en el sentido positivo del eje X. En el instante inicial (t = 0 s) y en
el origen (x = 0m) la elongación es y = +0’5 m. Hallar: a) la ecuación de la onda; b) la
diferencia de fase entre dos puntos separados 0’2 m; y c) la velocidad y aceleración
máximas de un punto del medio. (3 puntos)
a) Escribimos la ecuación de una onda que se propaga en el sentido positivo del eje x y
vamos calculando las magnitudes que necesitamos.
( ) ( )
( ) ( )0
1
p
p
0
φxπ20tπ200cos5,0t,xy
mπ20
1,0
π2
λ
π2
k
m1,0
100
10
f
v
λ;fλv
s/radπ200fπ2ω
φkxtωcosAt,xy
+−=
===
====
==
+−=
−
Sustituyendo x = 0 m y t = 0 s, comprobamos que el coseno vale la unidad cuando el
desfase inicial ϕ0 = 0, de modo que la ecuación queda:
( ) ( )xπ20tπ200cos5,0t,xy −=
b) Restamos las fases:
( ) ( ) ( ) radπ42,0·π20xxπ20xπ20tπ200xπ20tπ200 1221 ==−=−−−
c) Derivando la elongación obtenemos la ecuación de la velocidad y derivando esta
obtenemos la de la aceleración.
( ) ( ) s/mπ100v;xπ20tπ200sen5,0·π200t,xv max =−−=
( ) ( ) ( ) 22
max
2
s/mπ20000a;xπ20tπ200cos5,0·π200t,xa =−−=

CASTILLA LA MANCHA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº
1
P (3,75 puntos.) Una onda armónica sinusoidal se propaga en el sentido positivo del eje
OX con una frecuencia de 100 Hz, con una velocidad de 500 m/s y tiene una amplitud
de 15 cm. Calcula:
a) La ecuación de onda más general.
b) La separación entre dos puntos cuya diferencia de fase, en un cierto instante, es de
/5 radianes.
c) La diferencia de fase entre dos vibraciones de un mismo punto del espacio separadas
por un intervalo de tiempo de 2,5 · 10-3
s.






φ+νπ
λ
π
=φ+ω= · t··2-
· x·2
a) Para obtener la ecuación de onda hay que determinar la velocidad de la onda que es:
v = λ · ν; por tanto, m5
100
500v
==
ν
=λ
Sustituyendo los parámetros en la ecuación:






π
π
=





π
π
= · t·200-
5
· x·2
sen·0,15· t100··2-
5
· x·2
sen·0,15y
b) Puesto que interesa la diferencia de fase sólo importa el argumento del seno. De igual manera
el instante de tiempo que se toma no importa, por tanto podemos tomar t = 0.
5
· x·2
;
5
· x·2 2
2
1
1
π
=φ
π
=φ φ1 = 2 · π · x1/5; φ2 = 2 · π · x2/5
5
x··2
5
· x·2
-
5
· x·2 12 ∆π
=
ππ
=φ∆
m5,0
·2
5
·5
·2
·5
x =
π
π
=
π
φ∆
=∆ ; o lo que es lo mismo
10
λ
.
c) Al igual que en el apartado anterior sólo interesa el argumento de la función, en este caso
para x = 0.
φ1 = 200 · π · t1 ; φ2 = 200 · π · t2
∆φ = 200 · π · ∆t = 200 · π · 2,5 · 10-3
= 0,5 · π

CASTILLA - LA MANCHA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS/ OPCIÓN A/ Nº 4
3. De una onda estacionaria con los dos extremos fijos, sabemos que los antinodos
están separados 1,5 m. Calcula la longitud de onda de las ondas sinusoidales que
interfieren para dar lugar a dicha onda estacionaria.
La distancia entre dos antinodos generados por dos ondas sinusoidales que interfieren entre sí
es la mitad de la longitud de las onda que interfieren, de manera que la distancia es:
2
d
λ
=
Finalmente la longitud de onda es, λ = 2 · d = 2 · 1,5 = 3 m

CASTILLA LA MANCHA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS/OPCIÓN A/PR. 1
Un extremo de una cuerda tensa horizontal de 4 m de longitud tiene un movimiento
oscilatorio armónico de dirección vertical; en el instante t = 0,3 s la elongación de ese
extremo es 2 cm. Se mide que la perturbación tarda en llegar de un extremo al otro de la
cuerda 0,9 s y que la distancia entre dos mínimos consecutivos es 1 m. Calcular:
a) La amplitud del movimiento ondulatorio
b) La velocidad del punto medio de la cuerda en el instante t = 1s.
c) el desfase entre dos puntos separados 1,5 m, en un instante dado.
a) La amplitud del movimiento es la misma que la del extremo, y por tanto es de 2 cm.
b) Para determinar la velocidad de un punto de la cuerda es necesario determinar la ecuación de
la oscilación.
La longitud de onda de la misma es de 1 m.
Para determinar el periodo hay que hacer uso de la velocidad de propagación que es:
T
v
λ
=
Por tanto: s225,0
9,0/4
1
v
T ==
λ
=
La ecuación de onda es: 




 π
−π=




 π
−
λ
π
= · t
225,0
·2
x··2sen·02,0· t
T
·2
x·
·2
sen·Ay
Por tanto, la velocidad transversal, derivada de la elongación con respecto al tiempo será:





 π
−π−=




 π
−π
π
−== · t
225,0
·2
x··2cos·56,0· t
225,0
·2
x··2sco·
225,0
·2
·02,0
dt
dy
v
Para la posición x = 2 m y t = 1 s, la velocidad tiene un valor: v = 0,53 m/s.
c) El desfase entre dos puntos, para una longitud de onda de 1 m es:
desfase = fase1 – fase2 = 2 · π · ∆x = 3 π = π

CASTILLA LA MANCHA / JUNIO99. COU / FÍSICA / VIBRACIONES Y
ONDAS/OPCIÓN A/CUESTIÓN 3
Por una cuerda se propaga una onda transversal de frecuencia 50 Hz. La diferencia de
fase entre dos puntos separados 2,5 cm es π/3 radianes, en un cierto instante fijo.
Calcula la diferencia de fase entre los estados de vibración, en un mismo punto, cuando
han transcurrido 0,45 s.
La ecuación general de una onda es: 





νπ−
λ
π
= · t··2x·
·2
sen·Ay
Para determinar la diferencia de fase en un pinto fijo y dos instantes de tiempo se tiene:
desfase = fase1 – fase2 = 2 · π · ν · ∆t = 2 · π · 50 · 0,45 = 45 · π radianes
Este desfase se comporta igual que un desfase de π radianes.

CASTILLA-LA MANCHA / SEPTIEMBRE 02. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
OPCIÓN B
Problema 1
Sometemos el extremo de una cuerda tensa a un vibrador que provoca la propagación de
una onda armónica de ecuación Y(x,t) = 0,1· sen(0,8ππ t-160ππx) expresada en el sistema
internacional de unidades.
a) Determina amplitud, velocidad de propagación y longitud de onda.
b) Determina la velocidad de vibración de un punto de la cuerda que se encuentra a 10
cm del vibrador en el instante t = 0,5 s. ¿Qué tipo de movimiento describe dicho
punto?
a) La ecuación general de una onda viene dada por la siguiente expresión:






λ
−π=
x
T
t
2sen·A)t,x(Y
Identificando los términos con la ecuación del enunciado:
m/s0,005v
m0,0125ë
0,1A
==
λ
=
=⇒π=
λ
π
=⇒π=
π
=
π−π=
5,2
0125,0
T
160
2
s5,2T8,0
T
2
)x160t8,0(sen·1,0)t,x(Y
b) Derivando la posición, se obtiene la ecuación de la velocidad:
m/s0,16, =π−ππ=
π−ππ=
)1,0·1605,0·8,0·cos(8,0·1,0)5,01,0(V
)x160t8,0·cos(8,0·1,0)t,x(V
Realiza un movimiento armónico simple

CASTILLA LA MANCHA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 1
Podemos describir una onda armónica sinusoidal mediante la siguiente función de
onda en el SI:
y(x, t) = 1,25 · sen(79 · t -13 · x + /4). Calcula:
a) La elongación inicial y la velocidad inicial, en el origen de coordenadas.
b) La frecuencia y la velocidad de propagación.
c) La diferencia de fase entre dos puntos separados 5 m en el instante t = 3 s.
a) Para el punto inicial y tiempo inicial la elongación es: y(0, 0) = 1,25 · sen (π/4) = 0,884 m.
La fórmula general de la velocidad de movimiento de la onda transversal, no de la velocidad de
propagación, se calcula derivando parcialmente con respecto al tiempo, considerando la
posición fija. El resultado es: v(x, y) = 1,25 · 79 · cos(79 · t -13 · x + π/4)
Por tanto en el origen e instante inicial v (0, 0) = 98,75 · cos (π/4) = 69,8 m · s-1
b) La forma general de la ecuación de una onda es: )· x
·2
-· t··cos(2·At)y(x, φ+
λ
π
νπ=
Por tanto la frecuencia es: Hz6,12
·2
79
=
π
=ν
La longitud de onda es: m48,0
k
·2
=
π
=λ
Finalmente la velocidad de propagación se define como:
1-
s·m6,0512,6·0,48·
T
v ==νλ=
λ
=
c) La diferencia de fase entre dos puntos separados 5 m y t = 3 s es:
rad65/4)· x13-· t79(-/45)(x·13-· t7912 =π+π++=φ−φ=φ∆

CASTILLA LA MANCHA / SEPT99. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS/OPCIÓN A/PR.1
Una onda sinusoidal transversal que se propaga de izquierda a derecha tiene una
longitud de onda de 20 m, una amplitud de 4 m y una velocidad de propagación de 200
m/s. Calcula:
a) La ecuación de onda (supóngase la fase inicial cero).
b) La velocidad transversal máxima de un punto afectado por la vibración.
c) La diferencia de fase, en un instante dado, entre dos puntos separados una
distancia de 5m.
a) Para determinar la ecuación de una onda se necesita conocer la frecuencia (ν) del movimiento.
La velocidad de propagación es: v = λ · ν. Por tanto la frecuencia es: Hz10
20
200v
==
λ
=ν
La ecuación de onda general es: 





νπ−
λ
π
= · t··2x·
·2
sen·Ay
Sustituyendo: ( )· t·20x··0,1sen·4· t10··2x·
20
·2
sen·4y π−π=





π−
π
=
b) La velocidad transversal, es la derivada de la elongación con respecto al tiempo:
( ) ( )· t·20x··0,1cos··80· t·20x··0,1cos·4··20
dt
dy
v π−ππ−=π−ππ−==
La velocidad será máxima cuando el coseno valga -1. Por tanto la velocidad será: 251,3 m/s.
c) El desfase entre dos puntos, para una longitud de onda de 1 m es:
π
=
π
=∆
λ
π
==
2
5·
20
·2
x·
·2
fase-fasedesfase 21

CASTILLA LA MANCHA / SETIEMBRE99 COU/FÍSICA/VIBRACIONES Y
Una onda transversal se propaga en un medio elástico y de ella conocemos los siguientes
datos: 40 Hz de frecuencia y 100 m/s de velocidad de propagación. Calcula la diferencia
de fase entre dos puntos del espacio separados 4 m y en un instante fijo, por ejemplo, t =
3 s.
La ecuación general de una onda es: 





νπ−
λ
π
= · t··2x·
·2
sen·Ay
En la que la fase es: · t··2x·
·2
fase νπ−
λ
π
=
Para determinar el desfase hay que conocer la longitud de la onda considerada, y puesto que la
velocidad de propagación es: v = λ · ν, se tiene que: m5,2
40
100v
==
ν
=λ
Para un cierto instante de tiempo el desfase es:
desfase = fase1 – fase2 = radianes·2,1·2,34·
5,2
·2
x·
·2
π=π=
π
=∆
λ
π

LA RIOJA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
CUESTIÓN 4
CUESTIONES
4.- Describe brevemente qué entiendes por polarización de una onda.
Las ondas transversales pueden vibrar en todas las direcciones del plano perpendicular a la
dirección de propagación. Sin embargo hay métodos que permiten restringir las direcciones
de vibración a una sola. Cuando se produce este hecho se dice que la onda está polarizada
linealmente.
La presencia de este fenómeno en cierto tipo de ondas (como es el caso de las luminosas)
permite justificar su naturaleza transversal.
La polarización de las ondas se puede producir por absorción selectiva. Este método
consiste en la atenuación de todas las direcciones de vibración excepto de una. Lo producen
de forma natural unos minerales denominados turmalinas, también el hombre ha fabricado
materiales sintéticos que producen el mismo efecto y que se denominan polaroides.
Otro método de polarización es por reflexión. Existe un ángulo de incidencia para el que la
luz reflejada aparece polarizada linealmente. Este ángulo se denomina ángulo de Brewster
y se caracteriza porque la suna de los ángulos incidente y reflejado es 90º.
Para el caso concreto de las ondas electromagnéticas hay dos tipos de polarización más
denominados polarización circular y elíptica en la que los vectores campo eléctrico y
campo magnético describen en un caso circunferencia y en otro elipses. Se obtienen a partir
de combinaciones de polarizaciones lineales.

OPCIÓN PROBLEMAS 1
OPCIÓN PROBLEMAS 1
A) Una onda estacionaria en una cuerda está representada por la siguiente función de
onda:
tπ60cosxπ4sen02,0)t,x(y =
donde x e y están expresados en metros y t en segundos. Determinar el máximo
desplazamiento y la máxima velocidad de un punto de la cuerda situado en
a) x = 1,10 m; b) x = 0,25 m; c) x = 0,50 m.
a) Al tratarse de una onda estacionaria, los puntos del medio vibran perpendicularmente a la
dirección original del desplazamiento de la onda, pero ahora cada uno de ellos con una amplitud
diferente, que viene fijada por la posición de la onda que estudiemos.
Para x = 1,10 m la ecuación se transforma en:
tπ6cos·019,0tπ6cos·π4,4sen·02,0)t(y ==
Como se comprueba al observar la ecuación la amplitud en ese punto es A1 = 0,019 m
La velocidad de vibración la calculamos derivando con respecto al tiempo:
tπ6sen·36,0tπ6sen·π6·019,0)t(v −=−=
La velocidad máxima es vmax = 0,36 m/s
b) Para x = 0,25 m se tiene:
0tπ6cos·πsen·02,0)t(y ==
La posición coincide con un nodo por tanto no vibra
c) Para x = 0,50 m
0tπ6cos·π2sen·02,0)t(y ==
Vuelve a coincidir con la posición de un nodo

ACTIVIDAD 1
CUESTIONES
1.-Una partícula de masa m empieza su movimiento a partir del reposo en x
=25 cm y oscila alrededor de su posición en equilibrio en x = 0 con un
período de 1,5 s. Escribir las ecuaciones que nos proporcionan: x en función
de t, la velocidad en función de t y la aceleración en función de t.
RESPUESTA:
La ecuación de un movimiento vibratorio armónico es:
( )0tcosAx φω +=
La frecuencia angular ω, la obtenemos a partir del valor del periodo.
3
4
T
2
f2
ππ
πω ===
El valor de la amplitud lo da el enunciado, A = 0,25 m.
En el instante inicial la partícula se encuentra en el extremo de su trayectoria.
º01cos;·cos25,025,0 000 =⇒== φφφ
La ecuación de la posición queda:
t
3
4
cos25,0x
π
=
La de la velocidad:
t
3
4
sen
3dt
dx
v
ππ
−==
La de la aceleración:
t
3
4
cos
9
4
dt
dv
a
2
ππ
−==

LA RIOJA / SEPTIEMBRE 05. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN 2 / PROBLEMA A
OPCIÓN PROBLEMAS 2
A) Un onda estacionaria sobre una cuerda tiene por ecuación y =
0,02cos(π/2)x cos40πt donde x e y se miden en metros y t en segundos. 1)
Escribir funciones de onda para dos trenes de ondas que al superponerse
producirán la onda estacionaria anterior. 2) Calcular la distancia que existe
entre dos nodos consecutivos. 3) Determinar la velocidad de un segmento
de cuerda situado en el punto x = 1 en cualquier instante.
RESPUESTA:
Superponemos dos ondas con las mismas características que viajan en sentidos
contrarios:
( ) ( )tkxcosAtkxcosAyyy 21 ωω ++−=+=
Desarrollamos los cosenos de una suma y una diferencia:
[ ]
tcoskxcosA2y
tsensenkxtcoskxcostsensenkxtcoskxcosAy
ω
ωωωω
=
++−=
Comparando con la ecuación de ondas dada obtenemos los valores de las magnitudes
fundamentales que definen el movimiento ondulatorio.
t40;
2
k
01,0A02,0A2
πω
π
==
=⇒=
1) Las funciones de onda que se superponen son:
⎟
⎠
⎞
⎜
⎝
⎛
+=⎟
⎠
⎞
⎜
⎝
⎛
−= t40x
2
cos01,0y;t40x
2
cos01,0y 21 π
π
π
π
2) La distancia entre dos nodos consecutivos es la mitad de la longitud de la onda.
m4;
2
2
k === λ
π
λ
π
La distancia entre dos nodos consecutivos es 2 m.
3) En el punto x = 1 se produce un movimiento vibratorio armónico simple de
ecuación:
0t40cos1·
2
·cos01,0·2y =⎟
⎠
⎞
⎜
⎝
⎛
= π
π
Se trata de un nodo por lo tanto su velocidad es siempre nula.

LA RIOJA / JUNIO 01. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
Por una cuerda tensa se transmiten simultáneamente dos ondas transversales cuyas
ecuaciones, utilizando el Sistema Internacional, son:
y1 = 0,04 sen (10 x – 600 t)
y2 = 0,04 sen (10 x + 600 t)
Escribe la ecuación de la perturbación que aparece en la cuerda.
Cuando dos ondas coinciden la onda neta es la suma de ambas:
y = y1 + y2 = 0,04 (sen (10 x – 600 t) + sen (10 x + 600 t))
La suma de las dos ondas sigue la regla:
2
-
cos
2
sen2sensen
βαβα
βα
+
=+
Sustituyendo se obtienen la ecuación de la onda
y = 0,04 · 2 sen 10x cos 600 t m

LA RIOJA / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
CUESTIONES
2.- La frecuencia de una oscilación armónica simple se duplica de 0,25 Hz a 0,50 Hz
¿Cuál es el cambio en el periodo de oscilación?
La frecuencia es el inverso del periodo, de modo que si se duplica la frecuencia, el periodo
se ve reducido a la mitad.
s2T;
s2
1
Hz50,0s4T;
s4
1
Hz25,0
2
T
1
T
2
υ2;
T
1
υ
====
===

LA RIOJA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/
CUESTIÓN 3
Una onda armónica en un hilo tiene una amplitud de 15 mm, una longitud de 2,4 m y una
velocidad de 3,5 m/s. a) Determinar el periodo, la frecuencia y la frecuencia angular. b)
Escribir su ecuación suponiendo que se mueve en el sentido positivo del eje de las x.
a) La velocidad de propagación de una onda está relacionada con la longitud de onda y con el
periodo, de manera que: v = λ/T, por tanto: T = λ/v = 2,4/3,5 = 0,686 s
La frecuencia es la inversa del periodo: ν = T-1
= 0,686-1
= 1,46 Hz
Finalmente la frecuencia angular es: ω = 2 · π · ν = 2 · π · 1,46 = 2,92 rad · s-1
b) La ecuación general de una onda es: 





ω−
λ
π
= · tx·
·2
sen·Ay , sustituyendo se tiene:
( )· t92,2x·2,62sen·015,0· t92,2x·
4,2
·2
sen·015,0y −=





−
π
= m

CUESTIÓN 4
Describe brevemente qué entiendes por polarización de una onda.
Las ondas transversales son ondas cuya amplitud es perpendicular al movimiento. Cuando está
amplitud está restringida a un plano se dice que la onda está polarizada, y la dirección, o plano, de
polarización es la que contiene la dirección de la amplitud de la onda.

OPCIÓN 1/PR. A
A) Dos ondas que se mueven por una cuerda en la misma dirección y sentido, tienen la
misma frecuencia de 100 Hz, una longitud de onda de 2 cm y un amplitud de 0,02 m. a)
¿Cuál será la amplitud de la onda resultante si las dos ondas difieren en fase en π/3? b)
¿Y si difieren en π/6? c) ¿Cuál es la diferencia de fase entre las dos ondas si la amplitud
de la onda resultante es 0,02 que es la misma que la que poseen ambas componentes?
La ecuaciones de las ondas que se propagan por la cuerda son:






φ+νπ−
λ
π
=






νπ−
λ
π
=
· t··2x·
·2
sen·Ay
· t··2x·
·2
sen·Ay
2
1
El resultado de la suma de estas ondas es una tercera onda que se propaga con la misma longitud
de onda y frecuencia que cada una de las iniciales.





 φ
−Θ=
2
sen·Ay1 y 




 φ
+Θ=
2
sen·Ay2 si tenemos que
2
· t··2x·
·2 φ
+νπ−
λ
π
=Θ
La suma del seno de una suma mas una diferencia es:
y = 2A · cos ( )Θ




 φ
= sen·
2
cos·A2y
o lo que es lo mismo:





 φ
+νπ−
λ
π





 φ
=
2
· t··2x·
·2
sen·
2
cos·A2y
Por tanto la amplitud es: 




 φ
2
cos·A2
a) El desfase es π/3, por tanto: amplitud = m0346,0
6
cos·0,02·2
2
3/
cos·A2 =




 π
=




 π
b) El desfase es π/6: amplitud = m0386,0
12
cos·0,02·2
2
6/
cos·A2 =




 π
=




 π
c) Si la amplitud es la misma que la de cada una de las componentes se tiene que cumplir que:
2
1
2
cos =




 φ
, es decir:
3
·2
32
π
=φ⇒
π
=
φ

LA RIOJA / SEPTIEMBRE 2000. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
CUESTIÓN 1
Dos ondas que tienen la misma frecuencia, longitud de onda y amplitud, se están
moviendo en la misma dirección y sentido. Si su diferencia de fase es π/2 y cada una de
ellas tiene una amplitud de 0,05 m, hallar la amplitud de la onda resultante.
La suma de las dos ondas es: y = y1 + y2 = 0,05 sen (kx – ωt) + 0,05 sen (kx – ωt + π/2)
El valor de la suma es: sen A + sen B = 2 sen
2
BA +
cos
2
BA −
y = 0,05 · 2 · sen (kx – ωt + π/4) cos π/4 = 0,05 · 2 ·
2
2
sen (kx – ωt + π/4)
y = 0,071 sen (kx – ωt + π/4)

LA RIOJA / SEPTIEMBRE 2000. SELECTIVIDAD / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN 2 / TEORÍA
Tipos de ondas. Magnitudes que describen una onda.
Las ondas pueden ser longitudinales o transversales, dependiendo de si la oscilación es paralela al
sentido de propagación como en el sonido o perpendicular a ella como en la luz. Además las
ondas pueden ser estacionarias cuando no se desplazan, como en una guitarra, o pueden
desplazarse como la luz o el sonido.
Una onda queda determinada en función de la amplitud de la oscilación, la longitud de onda, el
periodo o frecuencia de la oscilación. En función de la longitud de onda y de la frecuencia queda
determinada la velocidad de propagación de la onda. La intensidad de la onda queda determinada
por la amplitud de la onda.

LA RIOJA / SEPTIEMBRE 2000. SELECTIVIDAD / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN 2 / PROBLEMA
En el centro de una piscina de 10 m de radio dejamos caer una piedra que da origen a
una onda sinusoidal en la superficie del agua. La longitud de onda de ese movimiento es
de 0,75 m y la onda tarda 10 s en llegar a la orilla. (a) Calcular el periodo y la frecuencia.
(b) Determinar la máxima elongación, sabiendo que al cabo de 0,25 s de producirse la
perturbación la elongación en el centro de la piscina es de 4 cm.
a) La velocidad de propagación es: v = λ · ν por tanto la frecuencia es:
Hz33,1
75,0
10/10v
==
λ
=ν
El periodo será: T = ν-1
= 1,33-1
= 0,75 s.
b) La oscilación en el punto central sigue la ecuación: y = A cos 2 π ν t
Sustituyendo:0,04 = A cos 2 π 1,33 · 0,25 = -0,5 A
Por tanto la amplitud máxima en módulo será: A = 0,04/0,5 = 0,08 m = 8 cm

LA RIOJA / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
CUESTIÓN 1
CUESTIONES
1.- La velocidad de propagación de una onda es de 330 m/s, y su frecuencia es de
1000 Hz. Calcular la distancia que existe entre dos partículas que se encuentran
desfasadas 120°.
Una longitud de onda es la distancia que hay entre dos puntos consecutivos que vibran en
fase o con un desfase de 360º. Para conocer la distancia entre dos puntos desfasados 120º,
calculamos la longitud de onda y realizamos una proporción:
m33,0
1000
330
υ
v
λ;λυv ====
Calculamos la parte de longitud de onda que es proporcional al desfase de 120º
m11,033,0·
360
120
x;
º120
x
º360
33,0
===

LA RIOJA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
2.- Por una cuerda tensa se transmiten simultáneamente dos ondas transversales cuyas
ecuaciones utilizando el Sistema Internacional son:
y1 = 0,04 · sen (10 · x - 600 · t) y2 = 0,04 · sen (10 · x + 600 · t)
Calcula la distancia entre dos nodos consecutivos.
La ecuación de la interferencia de las ondas es:
y = 0,04 · sen (10 · x - 600 · t) + 0,04 · sen (10 · x + 600 · t)
y = 0,08 · sen (10 · x) · cos (600 · t)
La distancia entre dos nodos es la distancia entre dos ceros de la función sen(10 · x).
10 · x = π ; x = 0,314 m

CASTILLA-LEÓN / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN A / CUESTIÓN A3
CUESTIÓN A3
Explique con claridad los siguientes conceptos: periodo de una onda, número de onda,
intensidad de una onda y enuncie el principio de Huygens. (2 puntos)
SOLUCIÓN
Periodo de una onda (T) es el intervalo de tiempo que transcurre entre dos estados
idénticos y sucesivos en la perturbación de un punto. Este valor coincide con el periodo del
movimiento vibratorio armónico simple del foco de la perturbación.
El número de onda (K) es una magnitud que surge como resultado de una simplificación
en la ecuación de ondas. Se define como el número de longitudes de onda que hay en la
longitud 2 π . Si dividimos 2 π por el valor del número de onda se obtiene la longitud de
onda del movimiento.
La intensidad de una onda (I) en un punto es la energía que pasa en cada unidad de
tiempo por la unidad de superficie situada perpendicularmente a la dirección de
propagación. LA intensidad es por tanto una potencia por unidad de superficie.
S
P
S·t
E
I ==
El principio de Huygens dice que cada punto del frente de ondas se comporta como un
foco emisor de ondas secundarias cuya envolvente constituye el nuevo frente de ondas.
Este principio solo es aplicable a ondas mecánicas en las que existen partículas reales que
vibran.
Una consecuencia del principio de Huygens es el fenómeno conocido como difracción.
La difracción se produce cuando una onda llega a un obstáculo cuyo tamaño es del mismo
orden de magnitud que su longitud de onda. Al actuar los puntos cercanos al obstáculo
como emisores secundarios el frente de ondas se modifica tomando una forma semejante a
la del obstáculo. El efecto que se percibe es que la onda bordea el obstáculo.

CASTILLA-LEÓN / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ OPCIÓN A / CUESTIÓN A3

CASTILLA-LEÓN / SEPTIEMBRE 04. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / OPCIÓN B / CUESTIÓN B3
CUESTIÓN B3
¿Qué se entiende por onda longitudinal y onda transversal? (0,3 puntos). Las ondas
sonoras ¿son longitudinales o transversales? (0,2 puntos). Explique las tres cualidades
del sonido: intensidad, tono y timbre (1,5 puntos)
SOLUCIÓN
La clasificación de las ondas en transversales y longitudinales se hace atendiendo a la
relación entre la dirección de vibración y la de desplazamiento. Las ondas longitudinales
son las que vibran en la misma dirección del desplazamiento y las ondas transversales las
que vibran de forma perpendicular al desplazamiento.
Las ondas sonoras son longitudinales, con frentes de onda esféricos en los que los puntos
del medio vibran hacia fuera y hacia adentro de la esfera formando zonas de compresión y
de enrarecimiento.
Cualidades del sonido:
Intensidad es la cantidad de sensación auditiva que produce un sonido, también
denominada sonoridad. Según su intensidad los sonidos se perciben como fuertes o débiles.
Físicamente la intensidad está relacionada con la mayor o menor amplitud de la onda
sonora.
El tono o altura esta relacionado con la característica física del sonido denominada
frecuencia. Nos permite distinguir los sonidos con altas frecuencias o agudos, de los que
tienen frecuencias bajas denominados graves.
El timbre es la característica que permite al oído humano distinguir dos sonidos con igual
intensidad y tono, pero emitidos por diferentes instrumentos musicales o personas. La
característica física relacionada con el timbre es la forma de onda.

CASTILLA-LEÓN / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN B
CUESTIÓN B3
Un punto realiza un movimiento vibratorio armónico simple de periodo T y
amplitud A, siendo nula su elongación en el instante inicial. Calcule el cociente
entre sus energías cinética y potencial:
a) en los instantes de tiempo t = T/12, t = T/8 y t = T/6 (1 punto).
b) cuando su elongación es x = A/4 , x = A/2 y x = A (1 punto).
RESPUESTA:
Las ecuaciones de la posición y la velocidad de un movimiento vibratorio armónico simple
son:
tω·cosωAv
tωsen·Ax
=
=
Y la relación entre sus energías:
22
2
22
2
p
c
xω
v
xωm
2
1
mv
2
1
E
E
==
a) Para
12
T
t = :
3
A·ω·4
4·3·ωA
E
E
2
3ωA
6
π
cosωAv
2
A
6
π
Asen
12
T
T
π2
Asenx
22
22
p
c
==
⎪
⎪
⎭
⎪⎪
⎬
⎫
==
===
Para
8
T
t =
1
2·A·ω·4
4·2·ωA
E
E
2
2ωA
4
π
cosωAv
2
2A
4
π
Asen
8
T
T
π2
Asenx
22
22
p
c
==
⎪
⎪
⎭
⎪
⎪
⎬
⎫
==
===
Para
6
T
t =

CASTILLA-LEÓN / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
3
1
3·A·ω·4
4·ωA
E
E
2
ωA
3
π
cosωAv
2
3A
3
π
Asen
6
T
T
π2
Asenx
22
22
p
c
==
⎪
⎪
⎭
⎪⎪
⎬
⎫
==
===
b) Sumando los valores delas dos energías se tiene que la energía total es:
22
pcT Aωm
2
1
EEE =+=
De modo que podemos expresar la energía cinética en función de la potencial como:
( )2222222
pTc xAωm
2
1
xωm
2
1
Aωm
2
1
EEE −=−=+=
Luego su relación es:
( )
2
22
22
222
p
c
x
xA
xωm
2
1
xAωm
2
1
E
E −
=
−
=
Para
4
A
x =
15
16
A
16
A15
16
A
16
A
A
E
E
2
2
2
2
2
p
c
==
−
=
Para
2
A
x =
3
4
A
4
A3
4
A
4
A
A
E
E
2
2
2
2
2
p
c
==
−
=
Para Ax =
0
A
AA
E
E
2
22
p
c
=
−
= la energía cinética vale cero.

CASTILLA-LEON / SEPTIEMBRE 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
OPCIÓN A / ACTIVIDAD 1
OPCIÓN A
PROBLEMA A1.
Una masa de 1 kg oscila unida a un resorte de constante k = 5 N/m, con un
movimiento armónico simple de amplitud 10-2
m.
a) Cuando la elongación es la mitad de la amplitud, calcule qué fracción
de la energía mecánica es cinética y qué fracción es potencial.(1,5
puntos).
b) ¿Cuánto vale la elongación en el punto en el cual la mitad de la energía
mecánica es cinética y la otra mitad potencial? (1,5 puntos).
RESPUESTA:
a) Las expresiones de la energía en función de la elongación son:
22
T
222
p
2222
c
Aωm
2
1
E
tωcoskA
2
1
kx
2
1
E
tωsenωmA
2
1
mv
2
1
E
tω·cosωAv
tωsen·Ax
=
⎪
⎭
⎪
⎬
⎫
==
==
⎭
⎬
⎫
=
=
Cuando
2
A
x = , la energía potencial vale:
22
2
2
p Aωm
8
1
4
A
ωm
2
1
E ==
comparándola con la energía total:
Tp
22
22
T
p
E
4
1
E;
4
1
Aωm
2
1
Aωm
8
1
E
E
===
La energía potencial es una cuarta parte de la energía mecánica total y la energía
cinética será tres cuartas partes de la energía mecánica total.
Tc E
4
3
E =
b) Lo calculamos a partir de la relación de la energía mecánica total con la potencial.
2
A
x
ωm
Aωm
2
1
x;Aωm
2
1
·
2
1
kx
2
1
;E
2
1
E 2
22
2222
Tp =⇒===

CASTILLA LEÓN / JUNIO 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN B
Problema 2
Un extremo de una cuerda tensa horizontal de 3 m de longitud está sometido a un
movimiento oscilatorio armónico. En el instante t = 4 s la elongación de ese punto es de 2
cm. Se comprueba que la onda tarda 0,9 s en llegar de un extremo a otro de la cuerda y
que la longitud de onda es de 1 m. Calcule:
a) La amplitud del movimiento ondulatorio (1,5 puntos).
b) La velocidad de vibración en el punto medio de la cuerda para t = 1 s(1,5 puntos).
a) La expresión de la ecuación general de la posición de la onda es y(x,t) = A· sen(ft + Kx)
De los datos del enunciado la longitud de onda λ, es 1 m, por lo que K = 1.
El enunciado dice que una onda tarda 0,9 s en llegar de un extremo a otro de la cuerda, o lo que
es lo mismo, en recorrer 3 m. Por la tanto la velocidad será 3,33 m/s.
Como v = λ· f , f = 3,33 Hz
El enunciado dice que en t = 4 s, la elongación del extremo es 2:
y(3,4) = A· sen(3,33· 4+3)=0,9· A = 0,02
A = 2,22 cm
b) Derivando la anterior ecuación se obtiene la de la velocidad:
V = A· 2πf· cos2π(ft + Kx)
Sustituyendo los valores anteriores:
V(1,5 , 1) = 0,0222· 2π· 3,33· cos2π(3,33· 1 + 1· 1,5) = 0,22 m/s

CASTILLA Y LEON / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 2
B1. Una partícula de masa 5 · 10-3
kg oscila por la acción de un resorte cuyo
movimiento viene dado por: x = 0,07 cos (3 · t + 1), con x en metros y t en segundos.
Determina:
a) La velocidad y la aceleración máximas de la partícula y los instantes en que las
magnitudes toman dichos valores máximos. ( 1 punto.)
b) E1 periodo de oscilación y la constante recuperadora del muelle. (l punto.)
a) El movimiento de la masa es: x = 0,07 · cos(3 · t + 1)
La velocidad es: ==
dt
dx
v -0,07 · 3 · sen(3 · t + 1) = -0,21 · sen(3 · t + 1)
El valor máximo de la velocidad es 0,21 y tiene lugar cuando: sen(3 · t + 1) = -1
Es decir: s24,1
3
1
2
t;
2
·3
1· t3 =−
π
=
π
=+
La aceleración es: ==
dt
dv
a -0,21 · 3 · cos(3 · t + 1) = -0,63 · cos(3 · t + 1)
El valor máximo de la aceleración es 0,63 y tiene lugar cuando: cos(3 · t + 1) = -1
Es decir: s71,0
3
1
t;1· t3 =
−π
=π=+
b) La ecuación de una oscilación es: 





φ+
π
=
T
· t·2
cos·Ax
Comparando con la ecuación problema se tiene que: s09,2
3
·2
T;3
T
·2
=
π
==
π
En los osciladores, el periodo de oscilación es:
k
m
··2T π=
Por tanto la constante del muelle es:
1-2
2
-32
2
2
m·N10·4,52
09,2
10·5··4
T
m··4
k −
=
π
=
π
=

CASTILLA Y LEÓN/ JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS/OPCION A/PR. 2
Cierta onda está descrita por la ecuación: Ψ(x, t) = 0,02 · sen(t - x/4), todo expresado en
unidades del SI. Determine:
a) La frecuencia de la onda y su velocidad de propagación.
b) La distancia existente entre dos puntos consecutivos que vibran con una diferencia de
fase de 120º.
a) La ecuación general de una onda es: ψ = A · sen(ω · t - k · x).
Por tanto la frecuencia angular es ω = 1 s-1
y la frecuencia será: ν = 1/2π =0,16 s-1
.
La velocidad de propagación es: 1-
s·m4
25,0
1
kT
v ==
ω
=
λ
=
b) Dos puntos que vibran con una diferencia de fase de 120º se diferencian 2π/3 radianes.
Por tanto: 2 π/3 = k · ∆x = ∆x/4. Por tanto: ∆x = 8,38 m

CASTILLA LEÓN / SEPTIEMBRE 02. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
OPCIÓN B
Problema 2
Una onda transversal se propaga según la ecuación:
y = 4· sen2ππ [(t/4)+(x/1,8)] (en unidades S.I.)
Determine:
a) La velocidad de propagación de la onda y la velocidad de vibración máxima de un
punto alcanzado por la onda (2 puntos).
b) La diferencia de fase, en un instante dado, de dos puntos separados 1 m en la
dirección de avance de la onda (1 punto).
a) La ecuación general de una onda es:






λ
+π=
x
ft2sen·Ay
Identificando términos con la ecuación dada en el enunciado se obtiene:
A = 4; f = 0,25 Hz; λ = 1,8 m
Para calcular la velocidad de propagación:
m/s0,45==λ=
λ
= 25,0·8,1f·
T
v
La velocidad de vibración máxima se obtiene derivando la ecuación de la posición:
V = 2π· f· A· cos2π(ft + Kx)
Vmax = 2π· f· A = 2ππ m/s
b)






+π=






+π=
8,1
x
4
t
2sen·4y
8,1
x
4
t
2sen·4y
2
2
1
1
( ) m3,49=−
π
=





+π−





+π=δ⇒ 21
21
xx
8,1
2
8,1
x
4
t
2
8,1
x
4
t
2

CASTILLA Y LEÓN/ SEPTIEMBRE99. LOGSE /FÍSICA/ VIBRACIONES Y
¿Qué clase de ondas son las sonoras? Exprese la ecuación que define su propagación,
enunciando las cualidades del sonido.
Las ondas sonoras son ondas longitudinales de presión. La ecuación que rige su movimiento es:
ψ(x, t) = A · cos(ω · t - k · x)
El sonido se caracteriza por su frecuencia y longitud de onda, ambas relacionadas por la
velocidad del sonido. Además tiene una cierta intensidad y puede tener un cierto timbre.

CASTILLA Y LEÓN/SEPTIEMBRE99. COU/FÍSICA /VIBRACIONES Y
ONDAS/BLOQUE C/ PR. 1
La ecuación de propagación de un movimiento ondulatorio en un medio material viene
dada por: y = 0,05 · cos(2 π (2 · t - 4 · x)), en unidades de Sistema Internacional. Calcule:
a) La velocidad de propagación.
b) La velocidad de vibración de la partícula situada a 0,50 m del origen en el instante t =
2 s.
La ecuación general de una onda es: 











λ
−π=
x
T
t
2cos·Ay
a) Identificando las partes, tenemos una ecuación con un periodo T = 0,5 s y una longitud de
onda λ = 0,25 m.
La velocidad de propagación se define como: 1-
s·m5,0
5,0
25,0
T
v ==
λ
=
b) La velocidad transversal de una onda se determina como la derivada con respecto al tiempo de
la velocidad, por tanto es:
v(x, t) = y’ = -0,05 · 4 · π · sen(2 π (2 · t - 4 · x))
Para x = 0,5 m, y = 2 s, la velocidad es: v = -0,05 · 4 · π · sen(2 π (2 · 2 - 4 · 0,5)) = 0

MADRID / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS / PARTE 2º /
CUESTIÓN 1
PARTE 2
CUESTIÓN 1
1. Una onda armónica transversal se propaga por una cuerda tensa de gran
longitud, y por ello, una partícula de la misma realiza un movimiento
armónico simple en la dirección perpendicular a la cuerda. El periodo de
dicho movimiento es de 3 s y la distancia que recorre la partícula entre
posiciones extremas es de 20 cm.
a) ¿Cuáles son los valores de la velocidad máxima y de la aceleración
máxima de oscilación de la partícula?
b) Si la distancia mínima que separa dos partículas de la cuerda que
oscilan en fase es de 60 cm, ¿Cuál será la velocidad de propagación
de la onda? ¿cuál es el número de onda?
RESPUESTA:
a) Consideramos solamente el movimiento vibratorio armónico simple que realiza la
partícula:
( )
t
3
π2
sen1,0y
cm10
2
20
A
s/rad
3
π2
T
π2
fπ2ω
φtωsenAy 0
=
⎪
⎭
⎪
⎬
⎫
==
===
+=
Derivando la expresión de la posición
s/m
3
π2,0
v;t
3
π2
cos
3
π2
·1,0v max ==
Derivando la velocidad
2
2
max s/m
9
π4,0
a;t
3
π2
sen
3
π2
·
3
π2,0
a =−=

MADRID / JUNIO 05 LOGSE / FÍSICA / VIBRACIONES Y ONDAS / PARTE 2º /
CUESTIÓN 1
b) Como la distancia mínima de dos partículas que oscilan en fase es la longitud de
onda, entonces λ = 0,6 m.
La velocidad de propagaciones:
s/m2,0
3
6,0
T
λ
v ===
El número de ondas es:
m/rad
3,0
π
6,0
π2
λ
π2
k ===

MADRID / JUNIO 05 LOGSE / FÍSICA /VIBRACIONES Y ONDAS
/ PRIMERA PARTE / CUESTIÓN 1
PRIMERA PARTE
CUESTIÓN 1
El nivel de intensidad sonora de la sirena de un barco es 60 dB a 10 m de
distancia. Suponiendo que la sirena es un foco emisor puntual, calcule:
a) El nivel de intensidad sonora a 1 km de distancia.
b) La distancia a la que la sirena deja de ser audible.
Dato: Intensidad umbral de audición I0 = 10-12
Wm-2
RESPUESTA:
a) Debemos calcular en primer lugar el valor de la intensidad a 1 km de distancia. Lo
hacemos en función de la intensidad a 10 m
4
10
6
2
10
1000
2
1000
2
10
210210002
10
I
10
10·I
I;)1000(π4·I)10(π4·I
)10(π4
P
I;
)1000(π4
P
I;
rπ4
P
I
===
===
Calculamos ahora la intensidad a partir de la intensidad sonora:
210
4
6
1000
26
1012
10
0
Wm10
10
10
I
Wm10I;
10
I
log1060
I
I
log10β
−−
−
−−
−
==
===
El nivel de intensidad sonora a 1 km de distancia será:
dB20
10
10
log10β 12
10
== −
−
b) La sirena deja de ser audible cuando su intensidad coincide con la intensidad
umbral de audición
2
12
2
10
rπ4
P
10;
)1000(π4
P
10 == −−
Igualando las potencias
m10r;10
10
10·10
r;)1000(π4·10rπ4·10 48
12
610
2212212
=⇒=== −
−
−−

MADRID / SEPTIEMBRE 05. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
REPERTORIO B / PROBLEMA 1
REPERTORIO B
Problema 1.- Dada la expresión matemática de una onda armónica
transversal que se propaga en una cuerda tensa de gran longitud:
y = 0,03 sen(2πt – πx) donde x e y están expresados en metros y t en
segundos.
a) ¿Cuál es la velocidad de propagación de la onda?
b) ¿Cuál es la expresión de la velocidad de oscilación de las partículas
de la cuerda? ¿cuál es la velocidad máxima de oscilación?
c) Para t = 0, ¿cuál es el valor del desplazamiento de los puntos de la
cuerda cuando x = 0,5 m y x = 1 m?
d) Para x = 1 m, ¿cuál es el desplazamiento cuando t = 0,5 s?
RESPUESTA:
a) Comparamos la ecuación dad con la ecuación general de una onda:
( )kxtsenAy −= ω
Como:
s/m2
2
k2
k
2
v
k
22
k
2
T
T
2
T
v pp ====
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=⇒=
=⇒=
=
π
πω
ω
π
π
π
λ
λ
π
ω
ππ
ωλ
b) Derivamos la expresión de la posición para obtener la expresión de la velocidad.
( )xt2·cos03,0·2
td
)t,x(dx
)t,x(v πππ −==
La máxima velocidad se obtiene cuando el coseno vale la unidad:
s/m188,003,0·2vmax == π

REPERTORIO B / PROBLEMA 1
c) Sustituimos para los valores dados:
( )
( ) m0sen·03,0)1,0(y
m1x,s0t
m03,05,0sen·03,0)5,0;0(y
m5,0x,s0t
=−=
==
−=−=
==
π
π
d) Sustituimos para los valores dados:
( ) m0sen·03,0)1;5,0(y
m1x,s5,0t
=−=
==
ππ

MADRID/JUNIO02.LOGSE/FÍSICA/VIBRACIONESYONDAS
PRIMERA PARTE
2. Escriba la expresión matemática de una onda armónica unidimensional como una
función de x (distancia) y t (tiempo) y que contenga las magnitudes indicadas en cada uno
de los siguientes apartados:
a) frecuencia angular ωω y velocidad de propagación v
b)período T y longitud de onda λλ
c) frecuencia angular ωω y número de onda k.
d) Explique por qué es una función doblemente periódica.
a) 





−ω=
v
x
tsen·A)t,x(y
b) 





λ
−π=⇒






π
=ω
λ
=
x
T
t
2sen·A)t,x(y
T
2
T
v
c) )kxt(sen·A)t,x(y
2
k
T
2
−ω=⇒






λ
π
=
π
=ω
d) La función es doblemente periódica, porque la función sinusoidal tiene una doble dependencia,
temporal y espacial.

MADRID / JUNIO98. LOGSE / FÍSICA / VIBRACIOENS Y ONDAS / OPCIÓN A/ Nº 1
1. Si se duplica la energía mecánica de un oscilador armónico, explica qué efecto tiene:
a) En la amplitud y la frecuencia de las oscilaciones.
b) En la velocidad y el periodo de oscilación.
1. La energía total de un oscilador depende de la constante de recuperación del muelle k y de la
amplitud máxima de oscilación A, según la ecuación: ET =
2
1
· k · A2
a) Si la energía se dobla, entonces ET' = 2 · ET
Por tanto: A'2
= 2 · A2
; A' = 1,414 · A.
La amplitud aumenta, mientras que la frecuencia de oscilación no lo hace puesto que es
independiente de la amplitud.
b) La velocidad de un oscilador, obtenida derivando la posición, es:
v(t) = A · ω · cos (ω · t + φ).
Si la amplitud aumenta la velocidad en cada instante de tiempo aumentará en igual medida:
v'(t) = 1,414 · v(t)
El periodo no variará al igual que no lo hace la frecuencia.

MADRID / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 2
2. a) ¿Qué son la intensidad y el tono de un sonido?
b) ¿De qué parámetros onda dependen.
a) La intensidad de un sonido se define como la potencia de un sonido dividido por la
superficie total de frente de ondas del sonido. Debido a esto, la intensidad del sonido es menor
cuanto más nos alejamos de la fuente emisora, aunque la potencia total de sonido emitida por la
fuente no varíe.
El tono de un sonido se relaciona con la frecuencia, y por tanto con la longitud de onda, del
sonido emitido. Es lo que se suele considerar como agudo, tonos de frecuencia elevada y
pequeña longitud de onda, o grave, tonos de baja frecuencia y gran longitud de onda.
b) La intensidad depende de la amplitud de la oscilación, ya que en el cálculo de la intensidad
promedio el efecto de la onda sinusoidal no tiene relevancia. Además esta amplitud, salvo en el
caso de sonidos confinados en tubos o casos similares, disminuye con la distancia a la fuente
sonora. El tono, como se ha dicho antes depende de la frecuencia de la onda, o lo que es lo
mismo de la longitud de onda de la misma.

MADRID A/ JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/
OPCIÓN A/CUESTIÓN 1
Dos sonidos tienen niveles de intensidad sonora de 50 dB y 70 dB, respectivamente.
Calcule cuál será la relación entre sus intensidades.
El decibelio se define como:








=
0I
I
log·10dB , donde I0 suele ser el umbral de audición. Por
tanto: I = I0 · 10dB/10
El cociente entre dos intensidades es: 10010
10
10
10·I
10·I
I
I 2
10/50
10/70
/10dB
0
/10dB
0
50
70
1
1
====

MADRID A/ JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/
Una onda armónica que se propaga por un medio unidimensional tiene una frecuencia
500 Hz y una velocidad de propagación de 350 m/s.
a) ¿Qué distancia mínima hay, en un cierto instante, entre dos puntos del medio que
oscilan con una diferencia de fase de 60°?
b) ¿Cuál es la diferencia de fase de oscilación, en un cierto punto, para un intervalo de
tiempo de 10-3
s?
a) Una diferencia de fase de 60º es π/3 radianes, que es λ/6.
La longitud de la onda es: m7,0
500
350v
==
ν
=λ
Finalmente, la diferencia de fase es: m12,0
6
7,0
6
==
λ
=φ∆
b) La frecuencia es de 500 Hz, por tanto el periodo es: T = ν-1
= 500-1
= 2 · 10-3
s. Entre dos
puntos que distan 10-3
s hay media oscilación, por tanto la fase será de 180º, π radianes.

PRIMERA PARTE / CUESTIÓN 2
PRIMERA PARTE
CUESTIÓN 2
La expresión matemática de una onda armónica es y(x, t) = 3 sen(200πt – 5x + π),
estando todas las magnitudes en unidades del SI. Determine:
a) La frecuencia y la longitud de onda.
b) La amplitud y la velocidad de propagación de la onda.
La expresión matemática de la onda viene dada por: y(x, t) = A sen(ω t – k x + δ0)
o también y(x, t) = A sen(2πυ t – (2π/λ) x + δ0)
Por tanto comparando los términos semejantes:
a) La frecuencia, Hz100
2
π200
υ;πυ2π200 ===
La longitud de onda, m
5
π2
λ;
λ
π2
5 ==
b) La amplitud, A = 3 m
La velocidad de propagación, s/mπ40λυv;
υ
v
λ ===

MADRID / SEPTIEMBRE99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/
Una masa m oscila en el extremo de un resorte vertical con una frecuencia de 1 Hz y una
amplitud de 5 cm. Cuando se añade otra masa de 300 g, la frecuencia de oscilación es de
0,5 Hz. Determine:
a) El valor de la masa m y de la constante recuperadora del resorte.
b) El valor de la amplitud de oscilación en el segundo caso si la energía mecánica del
sistema es la misma en ambos casos.
a) La frecuencia de un movimiento oscilatorio con una masa es:
m
k
·2
1
1
π
=ν
Cuando se añade la segunda masa tenemos:
mM
k
·2
1
2
+π
=ν
El cociente entre ambas es:
m
mM
2
1 +
=
ν
ν
Por tanto: kg1,01
5,0
1
·3,01·Mm
12
12
2
1
=








−








=










−








ν
ν
=
−−
La constante recuperadora es tal que: ( ) ( ) N/m95,31,0·1··2m···2k 22
1 =π=νπ=
b) La energía total de un oscilador es: E =
2
1
· k · xmax
2
Por tanto, como la energía total no depende de la masa en movimiento, la amplitud de la
oscilación será la misma: 5 cm.

R. MURCIA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
BLOQUE A / PREGUNTA TEÓRICA A1
PREGUNTA TEÓRICA A1
A.1 Energía del movimiento armónico simple
La energía mecánica de una partícula cualquiera es la suma de sus energías cinética y
potencial. En el caso de una partícula sometida a un movimiento armónico simple y
tomando como ecuación de la posición:
)φtωcos(Ax 0+=
la velocidad sería:
)φtω(senωAv 0+−=
por tanto las energías serán:
)φtω(senAωm
2
1
mv
2
1
E 0
2222
c +==
)φtω(cosAωm
2
1
kx
2
1
E 0
2222
p +==
Sumando ambas: 22
pcm Aωm
2
1
EEE =+= , valor que se mantiene siempre constante.

BLOQUE D/ CUESTIÓN D2
CUESTIÓN D2
D.2 ¿Cuál es el nivel de intensidad de una onda sonora de 5·10-3
W/m2
?
El nivel de intensidad sonora de una onda de intensidad I es:
0I
I
logβ =
Donde I0 = 10-12
W/m es la intensidad umbral.
Con los datos de que disponemos:
B7,9
10
10·5
logβ 12
3
== −
−
El resultado se suele dar en decibelios, b = 97 dB

PROBLEMA 2
PROBLEMA 2
P.2 Una antena de telefonía móvil emite radiación de 900 MHz con una potencia de
1500 W. Calcule:
a) La longitud de onda de la radiación emitida. (1 punto)
b) La intensidad de la radiación a una distancia de 50 m de la antena. (1 punto)
c) El número de fotones emitidos por la antena durante un segundo. (1 punto)
(Dato: h = 6.63·10-34
J·s.)
a) Como se trata de una radiación electromagnética:
m
3
1
10·900
10·3
f
c
λcf·λ 6
8
===⇒=
b) La intensidad se puede calcular como la potencia por unidad de superficie:
( )
2
22
m/W048,0
50π4
1500
rπ4
P
I ===
c) La energía de una onda electromagnética se puede escribir como:
E = h·f
Calculamos la energía de los fotones a partir de dicha expresión
J10·967,510·900·10·63,6f·hE 25634 −−
===
Como la potencia es la energía por unidad de tiempo, cada segundo la energía emitida será:
J1500t·PE;
t
E
P ===
Dividiendo este valor entre la energía que porta cada fotón se obtienen el número de
fotones:
fotones10·51,2
10·967,5
1500
E
E
fotonesºn 27
25
fot
=== −

MURCIA / JUNIO 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
CUESTIONES
BLOQUE C
1- ¿Cuál es la intensidad de una onda sonora de 85 dB?
Para calcular la intensidad sonora en dB se utiliza la siguiente expresión:
0I
I
·log10=β
En este caso el dato es la intensidad sonora, 85 dB. Conocida β e I0 = 10-12
W.m-2
, se puede
calcular I:
24
W·m3,16·10 −−
β
== 0
10
I·10I
2- Una muestra radiactiva contiene en el instante actual la quinta parte de los núcleos
que poseía hace cuatro días. ¿Cuál es su vida media?
El número de núcleos de una muestra de material radiactivo disminuye de manera exponencial
con el tiempo.
t
0 e·NN λ−
=
Con los datos que proporciona el enunciado se puede obtener el valor de λ:
1-
0
días4023,0
5
1
·ln
4
1
N
N
·ln
t
1
=





−=







−=λ
Por otro lado introduciendo este valor obtenido dentro de la fórmula de la vida media:
días1,72==
λ
=
4023,0
2ln2ln
t
2
1

MURCIA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 6
8. Una onda en una cuerda de 0,01 kg/m de densidad lineal viene dada por la ecuación:
y(x, t) = 0,2 · sen( · x + 100 · · t) m
a) La frecuencia de la onda. (1 punto.)
b) La velocidad de propagación de las ondas en la cuerda. (1 punto.)
c) La potencia que transporta la onda. (1 punto.)
La ecuación de la onda problema es: y(x, t) = 0,2 · sen (π · x + 100 · π · t) m
a) Las ecuación general de una onda que se mueve hacia valores negativos del eje de las x, como
es el caso de la ecuación del enunciado, tienen la siguiente fórmula general:






ω+
λ
π
= · t
x··2
sen·Ay (m)
Por tanto, igualando los distintos términos se obtiene que: ω = 2 · π · f = 100 · π
Y finalmente, el valor de la frecuencia es: f = 50 Hz
b) La velocidad se establece como el cociente entre la longitud de onda (λ) y el periodo de la
oscilación (T = f-1
), o lo que es lo mismo, v = λ · f.
En este caso la longitud de la onda es: π=
λ
π·2
; λ = 2 m
Finalmente: v = λ · f = 2 · 50 = 100 m · s-1
Hay que tener en cuenta que la onda se propaga hacia valores de x negativos, por tanto la
velocidad vectorial es: -1
s·mi100-v
rr
=
c) La potencia que transporta una onda se calcula con la ecuación:
t
A·f·m·p·2
t
W
P
222
==
Puesto que el dato que tenemos es el de la densidad lineal hay utilizar que:
· v
t
l·
t
m
ρ=
ρ
=
Haciendo uso de esta relación y sustituyendo los valores en la ecuación inicial, se obtiene que
la potencia de la onda es:
P = 2 · π2
· ρ · v · f2
· A2
= 2 · π2
· 0,01 · 100 · 502
· 0,22
= 1 974 W

REGIÓN DE MURCIA / JUNIO 01. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
¿Cuál es el nivel de intensidad de una onda sonora de 3 · 10-4
W/m2
?
El nivel de intensidad de las ondas sonoras se marca en decibelios comparado con la densidad de
potencia que se toma como referencia que es el nivel auditivo, que se encuentra en 10-12
W/m2
.
dB77,84
10
10·3
log10 12
-4
== −
β

BLOQUE B / PREGUNTA 1
PREGUNTAS TEÓRICAS
BLOQUE B
B.1 Energía del movimiento armónico simple
La energía mecánica de una partícula cualquiera es la suma de sus energías cinética y
potencial. En el caso de una partícula sometida a un movimiento armónico simple y
tomando como ecuación de la posición:
)tωcos(Ax 0+=
la velocidad sería:
)tω(senωAv 0+−=
por tanto las energías serán:
)tω(senAωm
2
1
mv
2
1
E 0
2222
c +==
)tω(cosAωm
2
1
kx
2
1
E 0
2222
p +==
Sumando ambas: 22
pcm Aωm
2
1
EEE =+= , valor que se mantiene siempre constante.

BLOQUE D / PREGUNTA 1
CUESTIONES
Bloque D
D.1 Una cuerda de 40 cm con sus dos extremos fijos vibra en un modo con 2 nodos
internos. ¿Cuál es la longitud de onda de la vibración?
Al haber dos nodos entre los extremos fijos, se formarán 3 vientres, siendo cada uno de
ellos media longitud de onda. Por lo tanto los 40 cm están formando una onda completa y
media.
λ
L
cm67,26
3
40·2
3
L2
λ
2
λ3
L ===⇒=

R. MURCIA / JUNIO 03. SELECTIVIDAD / FÍSICA / VIBRACIONES Y
ONDAS / BLOQUE A / PREGUNTA 2
PREGUNTAS TEÓRICAS
BLOQUE A
A.2 Clasificación de las ondas
Para clasificar las ondas se utilizan dos criterios, su naturaleza y su dirección de vibración.
Según su naturaleza, las ondas se clasifican en mecánicas cuando necesitan un medio
material que sirva de soporte a la perturbación que se propaga, y en electromagnéticas
cuando no necesitan dicho medio.
Atendiendo a su dirección de vibración pueden ser longitudinales cuando la dirección de
vibración coincide con la de propagación o transversales cuando ambas direcciones son
perpendiculares.

R. MURCIA / JUNIO 03. SELECTIVIDAD / FÍSICA / VIBRACIONES Y
ONDAS / BLOQUE C / PREGUNTA 1
CUESTIÓNES
Bloque C
C.1 ¿Cómo varían con la distancia la amplitud y la intensidad de una onda esférica
(en ausencia de atenuación)?
En ausencia de atenuación, la única causa que puede hacer disminuir la amplitud de una
onda es la absorción.
La absorción depende un factor denominado coeficiente de absorción a. Cuando una onda
de amplitud inicia A penetra en un medio una distancia x el valor de su amplitud es:
x
0eAA α−
=
Como la intensidad es proporcional al cuadrado de la amplitud se cumple que:
x2
0eII α−
=

MURCIA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 1
1. Energía del movimiento armónico simple. (1 punto.)
En el movimiento armónico simple hay en todo momento un intercambio de energía mecánica
entre la energía cinética y la potencial. La ecuación general del movimiento es:
x = A · sen(ω · t)
La energía potencial es: EP =
2
1
· k · x2
=
2
1
· k · A2
· sen2
(ω · t)
La energía cinética es: EC =
2
1
· m · v2
=
2
1
· m · A2
· ω2
· sen2
(ω · t)
Finalmente, la energía total que es constante queda como: ETotal =
2
1
· k · A2

MURCIA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/CUESTIÓN 3
¿Cómo varían con la distancia la amplitud y la intensidad de una onda esférica (en
ausencia de atenuación)?
La energía que transporta todo un frente de ondas esférico es independiente de la distancia, por
tanto la intensidad disminuye con la distancia como:
2
r4
P
Area
Potencia
I
π
==
Puesto que la potencia es proporcional a la amplitud al cuadrado, tenemos que la amplitud
disminuirá inversamente proporcional con la distancia:
r
1
A α

MURCIA / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS/CUESTIÓN 2
Principio de Huygens.
El principio de Huygens indica que cada punto de un frente de onda primario sirve como foco de
ondas elementales secundarias que avanzan con una velocidad y frecuencia igual a las de la onda
primaria. El frente primario al cabo de cierto tiempo es la envolvente de estas ondas elementales.

MURCIA / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS/PR. 1
Una partícula de 2 kg de masa efectúa un movimiento unidimensional dado por:
x(t) = 5 cos (10 t) m. Calcule las siguientes magnitudes de la partícula:
a) Energía cinética en función del tiempo.
b) Fuerza que actúa sobre la partícula en el instante t = 0.
c) Energía potencial en función del tiempo.
a) La energía cinética de una partícula es: Ek =
2
1
m · v2
En una oscilación la velocidad es la derivada de la posición con respecto al tiempo, por tanto es:
v(t) = -50 sen(10 t) m · s-1
.
Por tanto la energía cinética es: Ek =
2
1
m · (-50 sen(10 t))2
= 2 500 sen2
(10 t) J.
b) La fuerza se define como: F(t) = m · a(t) = m · (-500 cos(10 t)) = -1 000 cos(10 t) N
Por tanto: F(0) = -1 000 N.
c) La energía potencial es: Ep =
2
1
· k · x2
Para determinar la constante sabemos que: F = m · a = -k · x
por tanto: 1-
m·N200
t)cos(10·5
t)cos(10·0001
x
a·m-
k ===
Sustituyendo tenemos la energía potencial:
Ep =
2
1
· 200 · (5 cos(10 t))2
= 2 500 · cos2
(10 t) J.

MURCIA / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
4. Un sonido de 2 m de longitud de onda en el aire penetra en el agua en donde se
mueve con una velocidad de 1 500 m · s-1
. ¿Cual es su longitud de onda en el agua?
La velocidad de propagación de una onda es:
T
v
λ
=
Puesto que al cambiar de medio el periodo de la onda, al igua que su frecuencia, no varía se
tiene la siguiente relación:
v'v
' λ
=
λ
Por tanto: m8,8
340
5001
·2
v
'v
·'' ==λ=λ

NAVARRA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
EJERCICIO 1 / CUESTIÓN 1
EJERCICIO 1
CUESTIÓN 1
1) La distancia entre los extremos de una cuerda de una guitarra es 66 cm. Si la
frecuencia fundamental del sonido que emite cuando se pulsa es 440 Hz, calcular:
a) La longitud de onda de la onda estacionaria generada en la cuerda.
b) La velocidad de propagación de la onda en la cuerda. (2,5 puntos)
a) En el armónico fundamental, entre los extremos fijos hay media longitud de onda. Una
longitud de onda será:
m32,166,0·2L·2λ ===
b) Conocidas la longitud de onda y la frecuencia, podemos calcular a velocidad a partir del
producto entre ambas:
s/m8,580440·32,1f·λvp ===

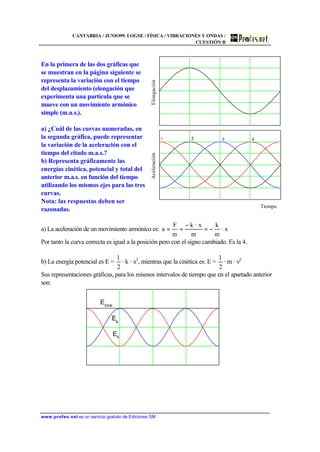
NAVARRA / SEPTIEMBRE 04. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / EJERCICO 1 / CUESTIÓN 4
EJERCICIO 1
4) Teoría: cinemática del movimiento armónico simple (m.a.s.): ecuaciones y
representaciones graficas de posición, velocidad y aceleración. (2,5 puntos)
La ecuación de un m.v.a.s. se obtiene a partir de la proyección de un movimiento circular
sobre una recta.
Cuando el punto P se desplaza por la circunferencia
de radio A el punto P’ se mueve de derecha a
izquierda y viceversa entre los extremos [-A, A].
Si la ecuación del movimiento circular es:
tωφφ 0 +=
La del movimiento vibratorio es:
( )0φtωcosAφcosAx +==
P
ωt+ϕ0
-A A
x P’
La función puede ser tanto un coseno como un seno ya que ambas difieren únicamente en
un desfase inicial, ϕ0 = π/2.
Derivando la expresión de la posición se obtiene la velocidad del m.v.a.s.
( )0φtωsenωA
dt
dx
v +−==
Derivando de nuevo se obtiene la ecuación de la aceleración:
( ) xωφtωcosωA
dt
xd
dt
dv
a 2
0
2
2
2
−=+−===
La aceleración es proporcional a la posición con distinto signo. Sus gráficas son:
a = -Aω2
cos ωt
x = A cos ωt
v = -Aω sen ωt
A
-Aω2
Aω

EJERCICIO 1
1) Una partícula de masa 0,1 kg realiza un movimiento armónico simple de las
siguientes características: Amplitud A = 1,7 cm; Periodo T = 0,2 s; en el
instante t = 0 se encuentra en la posición x = -1 cm.
a) Escribir la ecuación del movimiento. Representarla gráficamente.
b) Calcular su velocidad en el instante en que la partícula pasa por el origen x
= 0
c) Calcular su aceleración en ese mismo instante
d) Calcular su energía mecánica (2,5 puntos)
RESPUESTA:
a) Calculamos las magnitudes que intervienen en la ecuación
rad7,0º126
017,0
01,0
cosar);(cos017,001,0m01,0)0(x
s/rad10
2,0
2
T
2
00 πφφ
π
ππ
ω
==⎟
⎠
⎞
⎜
⎝
⎛ −
==−⇒−=
===
La ecuación queda:
( )ππ 7,0t10·cos017,0)t(x +=
b) Escribimos la ecuación de la velocidad
( )πππ 7,0t10sen·017,0·10
dt
)t(dx
)t(v +==
Como el movimiento se inicia en πφ 7,00 = , la primera vez que pasa por el origen es
cuando la fase vale
4
3π
φ = Para ese valor de la fase la velocidad es:
s/m17,0
4
3
sen·017,0·10)0x(v π
π
π =⎟
⎠
⎞
⎜
⎝
⎛
==

c) En un movimiento vibratorio armónico simple la aceleración es proporcional a la
posición.
x·a 2
ω−=
Como x = 0 m, entonces a = 0 m/s2
.
d) Al estar la partícula situada en x = 0 no tiene energía potencial, solo tiene energía
cinética.
( ) J014,017,0·1,0·
2
1
mv
2
1
E
22
=== π

EJERCICIO 1
2) Dos altavoces separados una distancia de 3,00 m están emitiendo sendas ondas
acústicas idénticas y en fase. Consideremos una recta paralela a la que une los
altavoces y que está a 8 m de la misma. Un oyente recorre dicha recta encontrando
puntos en los que la intensidad del sonido es máxima y otros en los que es mínima.
En concreto en O encuentra un máximo y en P, situado a 0,350 m de O, encuentra el
primer mínimo. Calcular la frecuencia de las ondas emitidas.
Dato: velocidad del sonido en el aire v = 340 m/s (2,5 puntos)
RESPUESTA:
Si hacemos interferir dos movimientos ondulatorios iguales:
( ) ( )
( ) ( )21121
2211
kxtsenAkxtsenAyyyy
kxtsenAykxtsenAy
−+−==+=
−=−=
ωω
ωω
Teniendo en cuenta la relación trigonométrica:
2
BA
cos
2
BA
sen2SenBsenA
−+
=+
La ecuación de onda queda:
⎟
⎠
⎞
⎜
⎝
⎛ +
−
−
=
2
xx
ktsen
2
xx
kcosA2y 2121
ω
El factor
2
xx
kcosA2 21 −
es la amplitud de la interferencia en cualquier punto del espacio.
La fase presenta un máximo cuando:
λπ
λ
π
π nxx;n
2
xx2
n
2
xx
k 21
2121
=−=
−
⇒=
−
La fase presenta un mínimo cuando:

λ
π
λ
ππ
)1n2(xx;
2
)1n2(
2
xx2
2
)1n2(
2
xx
k 21
2121
+=−+=
−
⇒+=
−
Como en nuestro caso nos encontramos en el primer mínimo:
( )
( )
m26,0
2
08,821,8
m21,835,05,18x
m08,835,05,18x
2
xx
22
2
22
1
12
=⇒=−
=++=
=−+=
=−
λ
λ
λ
Como conocemos la velocidad del sonido podemos calcular el periodo.
Hz1308
T
1
f
s10·65,7
340
26,0
v
T
T
v 4
==⇒
===⇒= −λλ

NAVARRA / JUNIO 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN A
Cuestión3
a) Explicar el fenómeno de la difracción.
b) Explicar porqué dos personas situadas una a cada lado de una esquina de forma que
no pueden verse, sin embargo sí pueden oírse
a) La difracción de ondas se produce cuando la onda se encuentra con un obstáculo cuyo tamaño
es del mismo orden de magnitud que su longitud de onda.
b) Por ejemplo, nos llega luz de un foco luminoso aunque no lo podamos ver directamente, o
cuando oímos los sonidos de un altavoz aunque esté detrás de un obstáculo; se puede decir que
las ondas doblan esquinas y bordean obstáculos, esto es debido al fenómeno de difracción y es
una consecuencia del principio de Huygens.
Por esta razón dos personas que no se ven pueden oírse, ya que se produce refracción de las
ondas, y cambia la dirección de propagación, por lo que pueden bordear la esquina.

EJERCICIO 2
Cuestión 1
1) Dada la onda descrita por la ecuación y = 0,20 sen π(20x + 100t) escrita en unidades
del Sistema Internacional calcular:
a) La amplitud, longitud de onda, periodo, frecuencia angular, frecuencia lineal,
velocidad y sentido de propagación de la onda.
b) La velocidad transversal de un punto situado a 0,30 m del origen cuando t = 5,0·10-3
s.
Interpretar físicamente el resultado (2,5 puntos)
a) Comparando la ecuación de la onda dada con una ecuación general de una onda, se tiene:
Amplitud, A = 0,2 m
Frecuencia angular, ω = 100π rad/s
Frecuencia lineal, ω = 2pν; Hz50
π2
π100
ν ==
Periodo, s02,0
50
1
ν
1
T ===
Longitud de onda, m1,0
π20
π2
K
π2
λ
λ
π2
K ===⇒=
Velocidad de propagación, s/m5
02,0
1,0
T
λ
vp ===
La onda se propaga en la dirección del eje OX y de derecha a izquierda, es decir en
sentido negativo de los valores de x, ya que el signo del argumento del argumento del
seno es positivo.
b) La velocidad de vibración se obtiene derivando la ecuación de la posición con respecto al
tiempo.
)t100x20(πcosπ20)t100x20(π·cosπ100·2,0
dt
)t,x(dy
)t,x(v +=+==
Su valor para x = 3 y t = 5·10-3
s es:
0
2
π
13cosπ20)10·5·1003·20(πcosπ20)10·5,3(v 33
=





=+= −−
m/s
Como la velocidad es nula, la partícula se encuentra en uno de los extremos de la vibración
cambiando el sentido de su velocidad.

NAVARRA / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
EJERCICIO 2
4) Teoría: El péndulo simple (2,5 puntos)
El péndulo simple consiste en un hilo inextensible de masa despreciable suspendido de un
extremo, del otro extremo pende un cuerpo de masa m que se puede considerar puntual.
Cuando la masa se separa del equilibrio una distancia A y se deja suelta, el péndulo oscila
entre
–A y A a ambos lados del punto de equilibrio. Este movimiento puede considerarse como
armónico simple cuando la separación A del punto de equilibrio es tan pequeña que se puede
despreciar la curvatura de la trayectoria.
Aplicando las leyes de Newton al cuerpo de masa m:
L θ
T
Px
Py P
Eje y:
ny
ny
maPT
amPT
=−
=+
rrr
Eje x:
θsenga;maθsenmg
amP
xx
xx
−==−
=
rr
Para ángulos muy pequeños, sen θ = θ de modo que la aceleración ax = -g θ
Si la longitud del péndulo es L, como el ángulo es pequeño, se puede hacer la aproximación:
x
L
g
axLθ x −=⇒=
Comparando esta aceleración con la del movimiento vibratorio armónico simple se tiene:
g
L
π2T
L
g
T
π4
;
L
g
ωxωa 2
2
22
=
==⇒−=
El periodo de un péndulo es independiente de la masa y de la amplitud de sus oscilaciones.

NAVARRA / JUNIO98. COU / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN B/ Nº 2
Clasificación de las ondas.
Las ondas se pueden clasificar de muchas maneras dependiendo del aspecto del movimiento
ondulatorio que se tenga en cuenta.
Una primera clasificación sería la de ondas estacionarias y ondas viajeras. Las primeras varían
sólo con el tiempo, mientras que las segundas tienen una variación espacio-temporal. Dos
casos son las cuerdas de guitarra y el sonido en el aire.
Otra posible clasificación es la de onda transversal o longitudinal. En las primeras la amplitud
de la onda se manifiesta como un desplazamiento perpendicular a la dirección de propagación,
mientras que en las segundas la amplitud se manifiesta a lo largo de la dirección de
propagación. Dos casos son la luz y el sonido respectivamente.

NAVARRA/SEPTIEMBRE02.LOGSE/FÍSICA/VIBRACIONESYONDAS
OPCIÓN A
Pregunta 1
Dos corchos que flotan en la superficie del agua de un estanque son alcanzados por una
onda que se produce en dicha superficie, tal que los sucesivos frentes de onda son rectas
paralelas entre sí que avanzan perpendicularmente a la recta que une ambos corchos. Se
observa que los corchos realizan 8 oscilaciones en 10 segundos, y que oscilan en
oposición de fase. Sabiendo que la distancia entre los corchos es 80 cm y que ésta es la
menor distancia entre puntos que oscilan en oposición de fase, calcular la velocidad de
propagación de la onda en el agua.
En el enunciado dice que los corchos oscilan en oposición de fase, por lo que se puede decir que
están separados un número impar de medias longitudes de onda. Como esta distancia es la menor
posible para estar en oposición de fase, se llega a la conclusión que los corchos están separados
λ/2:
cm160cm80
2
=λ⇒=
λ
La frecuencia de oscilación es conocida, 8 oscilaciones en 10 segundos ⇒ f = 0,8 s-1
Se tienen todos los datos necesarios para calcular la velocidad de propagación:
v = λ· f = 160· 10-2
· 0,8 = 1,28 m/s

NAVARRA/ SEPTIEMBRE 02. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
OPCIÓN A
Pregunta 3
Explicar cualitativamente el fenómeno de la polarización de la luz
El fenómeno de la polarización de la luz era conocido desde los trabajos de Christian Huygens
(1629-1695) pero fue estudiado a fondo por Jean Baptiste Biot (1774-1862) a principios del
siglo XIX. Este fenómeno de polarización sólo se da con ondas transversales, pero no con
longitudinales, ya que implica, una asimetría respecto del eje en la dirección de propagación. Si se
demuestra que un haz luminoso puede ser polarizado, se llega a la conclusión de que las ondas
luminosas son transversales.
Las ondas electromagnéticas son ondas planas transversales, ya que los campos eléctrico y
magnético oscilan perpendicularmente a la dirección de propagación. Por otro lado, los planos de
oscilación del campo eléctrico y magnético son normales entre sí. Consideraremos solo la
oscilación del campo eléctrico y asimilaremos las vibraciones luminosas a estas oscilaciones. Un
haz luminoso en el que las oscilaciones del campo eléctrico se verifiquen siempre en el mismo
plano se denominará, según hemos visto antes, haz luminoso polarizado.
La luz natural no está polarizada. La luz emitida por un manantial está constituida por una serie de
trenes de ondas procedentes de átomos distintos; en cada uno de estos trenes de ondas el campo
eléctrico oscila en un plano determinado, pero, en general, su orientación es distinta de unos a
otros.
Dado el enorme número de moléculas y átomos de un manantial luminoso, se comprende el gran
número de trenes de ondas que constituye un haz de luz y, por consiguiente, la existencia en éste
de ondas polarizadas en todas las direcciones transversales posibles.

ONDAS / EJERCICIO 1 / CUESTIÓN 1
EJERCICIO 1
1) Sea una cuerda tensa muy larga. Hacemos que uno de los extremos (O) realice un
movimiento armónico simple en una dirección perpendicular a la cuerda, de amplitud
A = 0,3 m y frecuencia f = 2 Hz, de forma que la perturbación se propaga a lo largo de la
cuerda con una velocidad de 5 m/s. Sabiendo que en el instante inicial la elongación del
punto O es nula:
a) Escribir la ecuación de onda
b) Hallar la elongación y velocidad transversal de un punto P situado a 10 m de O, 4 s
después de iniciado el movimiento. Interpretar el resultado. (2,5 puntos)
a) La ecuación de la onda es ( )φKxtωAsen)t,x(y +−= , calculamos los valores de K y ω:
π4
2
1
π2
T
π2
ω
5
π4
2
5
π2
λ
π2
K
s
2
1
f
1
T
m5,2
2
5
f
v
λfλ
T
λ
v
p
p
===
===






==
===⇒==
La ecuación queda: 





+−= φx
5
π4
tπ4sen3,0)t,x(y
Como para t = 0 en el origen de la perturbación, la elongación es nula el valor del desfase es
cero.






−= x
5
π4
tπ4sen3,0)t,x(y
b) La velocidad de vibración se obtiene derivando la ecuación de la posición con respecto al
tiempo.






−=





−== x
5
π4
tπ4cosπ2,1x
5
π4
tπ4·cosπ4·3,0
dt
)t,x(dy
)t,x(v
Su valor para x = 10 m y t = 4 s es:
( ) m0π8sen3,0π8π16sen3,010
5
π4
4·π4sen3,0)t,x(y ==−=





−=
s/mπ2,1π8cosπ2,110
5
π4
4π4cosπ2,1)4,10(v ==





−=

P. VASCO / JUNIO 04 LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
CUESTIÓN 1
CUESTIÓN 1
1. Describir el fenómeno de polarización de las ondas. ¿Qué tipo de ondas pueden ser
polarizadas? ¿Puede polarizarse el sonido? ¿Y la luz? Razonar la contestación.
Las ondas transversales pueden vibrar en todas las direcciones del plano perpendicular a la
dirección de propagación. Sin embargo hay métodos que permiten restringir las direcciones
de vibración a una sola. Cuando se produce este hecho se dice que la onda está polarizada
linealmente.
La presencia de este fenómeno en cierto tipo de ondas (como es el caso de las luminosas)
permite justificar su naturaleza transversal.
La polarización de las ondas se puede producir por absorción selectiva. Este método
consiste en la atenuación de todas las direcciones de vibración excepto de una. Lo producen
de forma natural unos minerales denominados turmalinas, también el hombre ha fabricado
materiales sintéticos que producen el mismo efecto y que se denominan polaroides.
Otro método de polarización es por reflexión. Existe un ángulo de incidencia para el que la
luz reflejada aparece polarizada linealmente. Este ángulo se denomina ángulo de Brewster
y se caracteriza porque la suna de los ángulos incidente y reflejado es 90º.
Para el caso concreto de las ondas electromagnéticas hay dos tipos de polarización más
denominados polarización circular y elíptica en la que los vectores campo eléctrico y
campo magnético describen en un caso circunferencia y en otro elipses. Se obtienen a partir
de combinaciones de polarizaciones lineales.
Como ya se ha indicado, las únicas ondas que se pueden polarizar son las transversales, de
modo que el sonido, que es una onda longitudinal, no se puede polarizar. En el caso de la
luz fue su capacidad para ser polarizada la que permitió definir esta como una onda
transversal.

PAÍS VASCO / JUNIO 02. LOGSE/FÍSICA/VIBRACIONESYONDAS
CUESTIONES
4. Ecuación del movimiento armónico simple. Indicar el significado de cada término.
Poner algún ejemplo.
El movimiento armónico simple (m.a.s.) es un movimiento rectilíneo cuyo desplazamiento x con
respecto a un punto fijo viene dado por una función del tipo x = A· cos(ωt + ϕ), siendo A, ω y ϕ
constantes.
La constante A, representa el valor máximo que puede tomar la elongación x y se llama amplitud.
La constante ϕϕ se llama desfase inicial y determina la elongación inicial x0 cuando t = 0, es decir
x0 = A· cosϕ.
La constante ωω, da una idea de la rapidez con que se mueve el oscilador, se llama frecuencia
angular o pulsación.
Ejemplos de movimientos armónico simple, el péndulo y el movimiento de vibración de un muelle.

PAÍS VASCO / JUNIO 03. LOGSE / FÍSICA / VIBRACIONES Y ONDAS /
BLOQUE B / PROBLEMA 2
PROBLEMAS
BLOQUE B
2. En una cuerda tensa se propaga una onda transversal de ecuación
y (x, t) = 2 sen 2π (10t – 0,1x) en unidades del S.I. Determinar
a) Periodo, longitud de onda y velocidad de propagación.
b) Velocidad y aceleración máximas en un punto de la cuerda.
c) Ecuación de otra onda idéntica que se propague en sentido contrario.
a) Comparando con la ecuación general de aun movimiento ondulatorio se tiene:
( ) 





−=−=
λ
x
T
t
π2senAkxtωsenA)t,x(y
El periodo: s1,0T;10
T
1
==
La longitud de onda: m10λ;1,0
λ
1
==
La velocidad de propagación: s/m100
1,0
10
T
λ
vp ===
b) Para calcular la velocidad y la aceleración máximas de un punto de la cuerda, derivamos
la ecuación del movimiento.
( )x1,0t10π2cosπ20·2
dt
)t,x(dy
)t,x(v −==
Como el coseno varía entre –1 y 1, el valor máximo de la velocidad será su coeficiente,
vmax = 40 π m/s
( )x1,0t10π2senπ20·π40
dt
)t,x(dv
)t,x(a −−==
Razonando como en el caso de la velocidad, amax = 800 π m/s2
.
c) Para que una onda se propague en sentido contrario, únicamente hay que cambiar el
signo del argumento del seno:
)0,1+(10= xtπ2sen2t)(x,y

PAÍS VASCO / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 3
1. Describe el fenómeno de polarización de las ondas. ¿Qué tipo de ondas pueden ser
polarizadas? ¿Puede polarizarse el sonido? ¿Y la luz? Razona la respuesta.
Una onda puede polarizarse cuando se trata de una onda transversal. El fenómeno de
polarización implica que la oscilación transversal puede suceder sólo en un plano, no oscilando
en la dirección perpendicular. Debido a esto la luz puede polarizarse porque es una onda
electromagnética transversal, pero no puede polarizarse el sonido, ya que es una onda
longitudinal.

PAÍS VASCO / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/BLOQUE A/
PR. 1
En el centro de una piscina circular de 6 m de radio se produce una perturbación que
origina un movimiento ondulatorio en la superficie del agua. La longitud de onda es de
0,50 m y tarda 12 s en llegar a la orilla. Calcular:
a) La frecuencia del movimiento ondulatorio.
b) La amplitud del mismo si al cabo de 0,25 s la elongación en el origen es de 4 cm.
c) La elongación en el instante t = 12 s en un punto situado a 6 m del foco emisor.
a) La velocidad del movimiento ondulatorio es: 1-
s·m5,0
12
6
t
d
v ===
Finalmente, la frecuencia es: Hz1
5,0
5,0v
==
λ
=ν
b) La oscilación del centro será de la forma A(t) = A0 · sen (ν · t), por tanto la amplitud máxima
será: cm4
)0,25·1··2sen(
4
)· t··2sen(
)t(A
A 0 =
π
=
νπ
=
c) Puesto que tarda 12 s en llegar la perturbación al extremo de la piscina la oscilación será como
en el instante inicial en el centro, es decir, la amplitud será 0.

PAÍS VASCO / JUNIO99. COU / FÍSICA / VIBRACIONES Y ONDAS/OPCIÓN B/
TEMA A
Ondas estacionarias en cuerdas.
Cuando una cuerda vibra lo que le sucede es que todos sus puntos tienen una posición que varía
con el tiempo. No todos los puntos vibran de manera igual, ya que los extremos de la cuerda
están fijos y es posible que algunos puntos de la cuerda tampoco oscilen. De esta manera, sólo
aquellas vibraciones cuya longitud de onda multiplicada por un número entero sea la longitud de la
cuerda, tendrán lugar. A estas ondas se les denomina estacionarias ya que la oscilación no se
propaga a lo largo de ella.

PAÍSVASCO/SEPTIEMBRE02.LOGSE/FÍSICA/VIBRACIONESYONDAS
PROBLEMAS
BLOQUE A
2. Una onda armónica se propaga por un medio elástico siguiendo la ecuación
y = 24· sen(2000t-5x) en unidades del S.I. Determinar:
a) Amplitud, frecuencia y longitud de onda de la misma.
b) El desfase que existirá entre dos puntos separados 0,2 m entre si a lo largo de la
dirección de propagación de la onda.
c) La ecuación de otra onda idéntica a la anterior que se propague en sentido contrario a
la dada.
a) Identificando los términos con la ecuación general:
b) m1==−=+−=δ 2,0·5)xx·(5x·5x·5 2112
c) Para obtener la ecuación idéntica a la anterior que se desplaza en sentido contrario basta con
cambiar el signo dentro del seno, y = 24· sen(2000t + 5x)
m
5
2ð
ë
s
ð
1000
f
24A
1
=⇒=
λ
π
=⇒=π
=






λ
−π=
−
5
2
2000f2
x
ft2sen·Ay

PAÍS VASCO / SEPTIEMBRE99. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
CUESTIÓN 2
Analogías y diferencias entre las ondas sonoras y luminosas.
Ambos son movimientos oscilatorios, pero las ondas sonoras se deben a cambios de presión en el
medio en que se mueven mientras que las ondas luminosas están formados por campos
electromagnéticos y, a diferencia del sonido, se pueden desplazar en el vacío. Además las
frecuencias y velocidades de propagación son muy diferentes, mientras que las longitudes de onda
pueden ser similares o diferentes. Por último, las ondas luminosas son ondas transversales
mientras que las sonoras son siempre longitudinales.

C. VALENCIANA / JUNIO 04. LOGSE / FÍSICA / VIBRACIONES Y ONDAS/
BLOQUE 2 / OPCIÓN A
BLOQUE 2
OPCIÓN A
Explica mediante un ejemplo el transporte de energía en una onda. ¿Existe un
transporte efectivo de masa?
Si observamos un corcho flotando sobre la superficie de un lago, y mediante una
perturbación, provocamos una onda en el agua, comprobaremos que cuando la onda
alcance al corcho lo desplazará verticalmente haciéndolo subir y bajar. Para que este hecho
se produzca debe existir transporte de energía por parte de la onda.
El mismo ejemplo del corcho sirve para comprobar que la onda no transporta materia ya
que el corcho siempre permanece en el mismo sitio, es decir no se desplaza en el sentido de
avance de la onda.
Otro ejemplo que podemos utilizar es el del sonido. En ocasiones ruidos de determinada
frecuencia son capaces de hacer vibrar el cristal de una ventana por efecto de la resonancia,
este hecho se produce porque las ondas sonoras transportan energía, sin embargo el sonido
nunca produce un transporte efectivo de las partículas de aire que se encargan de
transmitirlo, es decir, un sonido por muy fuerte que sea no es capaz de producir corrientes
de aire.

C. VALENCIANA / JUNIO 05. LOGSE / FÍSICA / VIBRACIONES Y ONDAS
/ BLOQUE 2 / OPCIÓN A
BLOQUE II - PROBLEMAS
Opción A
Se tiene un cuerpo de masa m = 10 kg
que realiza un movimiento armónico
simple. La figura adjunta es la
representación de su elongación y en
función del tiempo t. Se pide:
1. La ecuación matemática del
movimiento armónico y(t) con los
valores numéricos correspondientes,
que se tienen que deducir de la gráfica.
(1,2 puntos)
2. La velocidad de dicha partícula en
función del tiempo y su valor concreto en
t =5 s. (0,8 puntos)
RESPUESTA:
1. La ecuación de un movimiento vibratorio armónico simple es:
( )0tcosAy φω +=
A es la amplitud o máxima elongación que sufre la partícula que vibra. En la grafica se ve que su
valor es A = 4 mm.
ω es la frecuencia angular; .
T
2π
ω = Calculamos su valor a partir del valor del periodo T.
s/rad
612
2
s12T
ππ
ω ==⇒=
Calculamos 0φ a partir del valor inicial del movimiento:
32
1
cos;·cos004,0002,0;mm2)0(y 000
π
φφφ =⇒===
La ecuación queda:
⎟
⎠
⎞
⎜
⎝
⎛
+=
3
t
6
cos004,0y
ππ
2. Derivamos la ecuación de la posición y sustituimos:
s/m
6
002,0
36
5
sen·
6
·004,0)5(v
3
t
6
sen·
6
·004,0
dt
dy
v
ππππ
πππ
=⎟
⎠
⎞
⎜
⎝
⎛
+−=
⎟
⎠
⎞
⎜
⎝
⎛
+−==

C. VALENCIANA / SEPTIEMBRE 05. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS / BLOQUE 2 / OPCIÓN A
BLOQUE II – CUESTIONES
Opción A
Un cuerpo oscila con movimiento armónico simple cuya amplitud y período
son, respectivamente, 10 cm y 4 s. En el instante inicial, t =0 s, la elongación
vale 10 cm. Determina la elongación en el instante t =1 s.
RESPUESTA:
Escribimos la ecuación del movimiento vibratorio armónico simple:
( )0tcosAx φω +=
Calculamos las magnitudes que intervienen en la expresión dada:
01coscos1,0)0(x
s/rad
24
2
T
2
000 =⇒=⇒=
===
φφφ
πππ
ω
Conocidos los valores escribimos la ecuación y sustituimos:
m0
2
cos1,0)1(x
t
2
cos1,0)t(x
==
=
π
π

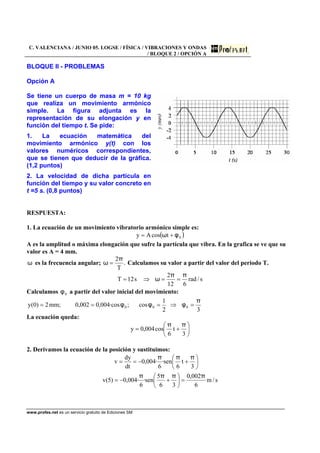
COMUNIDAD VALENCIANA / JUNIO 01. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
La ecuación de una onda que se propaga por una cuerda es:
y (x, t) = 8 sen[π (100 t – 8 x)]
donde x e y se miden en centímetros y t en segundos. Calcula el tiempo que tardará la
onda en recorrer una distancia de 25 m.
La ecuación de una onda es: 





−= xt
T
Ay
λ
ππ 22
sen
Dado que la velocidad es:
T
v
λ
= se puede calcular realizando el cociente entre el factor que
multiplica al tiempo dividido por el que multiplica a la posición. Por tanto:
cm/s5,12
8
100
==
π
π
v
Por tanto en recorrer 25 m tardará 200 s.

ONDAS
BLOQUE II
OPCIÓN A
Describe en qué consiste el efecto Doppler.
El efecto Doppler es un fenómeno ondulatorio que se produce cuando hay un movimiento
relativo entre un foco emisor de ondas y un observador. La frecuencia percibida por el
observador es distinta de la frecuencia emitida por el foco.

ONDAS
BLOQUE III
OPCIÓN A
Un foco luminoso puntual se encuentra situado en el fondo de un estanque lleno de agua
de n = 4/3 y a 1 metro de profundidad. Emite luz en todas las direcciones. En la
superficie del agua se observa una zona circular iluminada de radio R. Calcula el radio R
del círculo luminoso.
Los extremos del círculo luminoso vendrán dados por el ángulo límite λ a partir del cual se
produce el fenómeno de reflexión total y los rayos no salen a la superficie.
º59,48
4
3
sen)90(sen·1sen·
3
4
2sen·2n1sen·1n
=λ
=λ⇒=λ
ε=ε
Como nos piden el radio del círculo luminoso:
m1,13==⇒λ= )59,48(tg·1Rtg·hR

COMUNIDAD VALENCIANA / JUNIO 03. LOGSE / FÍSICA /
VIBRACIONES Y ONDAS / BLOQUE II / OPCIÓN A
BLOQUE II – CUESTIONES
Opción A
Un cuerpo dotado de movimiento armónico simple de 10 cm de amplitud, tarda 0,2 s
en describir una oscilación completa. Si en el instante t = 0 s su velocidad era nula y la
elongación positiva, determina
1. La ecuación que representa el movimiento del cuerpo
2. La velocidad del cuerpo en el instante t = 0,25 s.
La ecuación de un movimiento vibratorio armónico simple es: y = A cos (ωt + ϕ).
Su velocidad se obtiene derivando con respecto al tiempo la ecuación del movimiento:
v = - Aω sen (ωt + ϕ)
Si en el instante t = 0 la velocidad es nula el desfase debe ser cero, ϕ = 0
Se calcula el valor de ω a partir del dato del periodo:
s/radπ10
2,0
π2
T
π2
ω ===
1. La ecuación de este movimiento armónico es:
y = 0,1 cos (10πt)
2. La ecuación de la velocidad es:
v = - π sen (10πt)
v(0,25) = - π sen (10π·0,25) = - π sen (2,5π) = -π m/s

COMUNIDAD VALENCIANA / JUNIO98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN
A/ Nº 4
C2 Determina la ecuación de una onda armónica progresiva, de amplitud 10,
frecuencia 600 y velocidad 3 · 108
(unidades en el S.I.).






φ+νπ
λ
π
=φ+ω= · t··2-
· x·2
Para obtener la ecuación de onda hay que determinar la velocidad de la onda que es:
νλ=
λ
= ·
T
v ; por tanto, m10·5
600
10·3v 5
8
==
ν
=λ
Sustituyendo los parámetros se obtiene la ecuación de la onda:
· t)·2001-x10··sen(4·10·600··2-
10·5
· x·2
sen·10y 6-
5
ππ=





π
π
=

COM. VALENCIANA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS/PROBEMA 1/CUESTIÓN 2
Definir los conceptos de “onda longitudinal” y “onda transversal”. Proponer un ejemplo
de cada una e indicar las magnitudes físicas que se propagan.
Una onda longitudinal es aquella en la que los desplazamientos de los átomos, o de los elementos
cuyo movimiento crean la onda, tienen lugar en la misma dirección que la propagación de la onda.
Este es el caso del sonido, en el que se propaga una onda de presión.
En las ondas transversales los átomos, o campos que se propagan, se mueven
perpendicularmente a la propagación. Este es el caso de las ondas electromagnéticas, en las que
se propaga un campo eléctrico y uno magnéticos ambos perpendiculares a la propagación.

COMUNIDAD VALENCIANA / SEPTIEMBRE 02. LOGSE / FÍSICA /
VIBRACIONES Y ONDAS
BLOQUE II
OPCIÓN A
De una onda armónica se conoce la pulsación w = 100 s-1
y el número de ondas k = 50 m-
1
. Determina la velocidad, la frecuencia y el período de la onda.
Conocida la pulsación se pude calcular el período y la frecuencia.
1
s
ð
50
s
50
ð
−
==
=
π
=
π
=⇒
π
=
T
1
f
100
2
w
2
T
T
2
w
Con el número de ondas se puede calcular la longitud de onda, λ, y con la longitud de onda y el
período se obtiene la velocidad:
m/s2=
π
π
=
π
=
λ
=
50
50
2
T
k
2
T
v

C. VALENCIANA / SEPTIEMBRE 03. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS
BLOQUE II – PROBLEMAS
Opción A
Una onda armónica transversal progresiva tiene una amplitud de 3 cm, una longitud
de onda de 20 cm y se propaga con velocidad 5 m/s. Sabiendo que en t = 0 s la
elongación en el origen es 3 cm, se pide:
1. Ecuación de la onda. (0,7 puntos)
2. Velocidad transversal de un punto situado a 40 cm del foco en el instante t = 1 s. (0,7
puntos)
3. Diferencia de fase entre dos puntos separados 5 cm en un instante dado. (0,7 puntos)
1. La ecuación de una onda armónica viene dada por la expresión:
)kxtω(sen·A)t,x(y −=
Calculamos las magnitudes que desconocemos:
π10
2,0
π2
λ
π2
k ===
Para calcular ω hay que conocer previamente el periodo:
s/radπ50
04,0
π2
T
π2
ω
s04,0
5
2,0
v
λ
T;v
T
λ
===
====
Como para t = 0 s en el punto x = 0 la elongación es igual a A, el valor del seno debe ser la
unidad luego hay que introducir un desfase de π/2.






+−=
2
π
xπ10tπ50sen·03,0)t,x(y
2. Derivando con respecto al tiempo se obtiene la ecuación de la velocidad de vibración:
s/m0
2
π
·cosπ5,1
2
π
π4π50cosπ5,1)1;4,0(v
2
π
xπ10tπ50·cosπ·03,0·50)t,x(v
=





=





+−=






+−=
3. La longitud de la onda es 20 cm, esto quiere decir que cada 20 cm encontraremos puntos
que vibran en fase. Como 5 cm es la cuarta parte de la longitud de la onda, cualquier pareja
de puntos que se encuentren a 5 cm de distancia estarán desfasados la cuarta parte de la
longitud de onda.
4
λ
φ∆ =

ALICANTE / SEPTIEMBRE98. LOGSE / FÍSICA / VIBRACIONES Y ONDAS / OPCIÓN A/ Nº 4
C-2 Sea una onda armónica plana no amortiguada cuya longitud de onda es de 30 cm.
Calcular la diferencia de fase entre dos puntos del medio, separados una distancia de
1,5 m en la dirección de propagación de la onda.
La distancia de 1,5 m equivale a 5
3,0
5,1
= longitudes de onda. Por tanto la diferencia de fase es
de 5 · 2 · π = 10 · π. Puesto que es un múltiplo de 2 · π, los dos puntos se moverán
simultáneamente.

COM. VALENCIANA/SEPTIEMBRE99. LOGSE/FÍSICA/VIBRACIONES Y ONDAS
EJERCICIO 1º/CUESTIÓN 1
¿Qué se entiende por intensidad de una onda? ¿Qué relación existe entre la intensidad y
la amplitud de una onda esférica?
La intensidad de una onda es el cociente que hay entre la potencia que transporta una onda y la
superficie del frente de ondas. Por tanto es la potencia por unidad de superficie en una onda.
En las ondas esféricas la intensidad y la amplitud están relacionadas de manera que la intensidad
es proporcional al cuadrado de la amplitud, ya que la energía de un movimiento oscilatorio es
proporcional al cuadrado de su amplitud.

Movimiento Ondulatorio

Más contenido relacionado

La actualidad más candente

Similar a Movimiento Ondulatorio

Último

Movimiento Ondulatorio