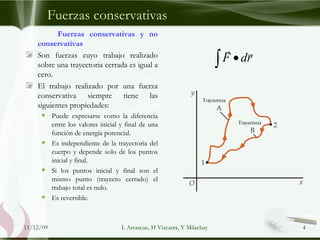
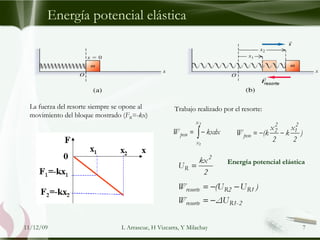
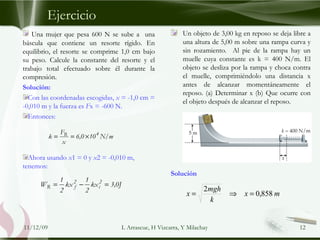
Este documento trata sobre la energía mecánica y su conservación. Explica la energía potencial gravitatoria y elástica, las fuerzas conservativas y no conservativas, y la conservación de la energía mecánica. Además, presenta varios ejemplos numéricos sobre la aplicación de estos conceptos.

1. Energía mecánica y su conservación Energía potencial gravitatoria y elástica. Fuerzas conservativas y no conservativas. Conservación de la energía mecánica.

2. Energía potencial U Existe una energía asociada a la posición de los cuerpos en un sistema. Este tipo de energía es una medida del potencial o posibilidad de efectuar trabajo. Calculemos el trabajo realizado por el peso del cuerpo de la figura mientras es trasladado desde y 1 hasta y 2 . La expresión muestra que podemos expresar el trabajo del peso en términos de los valores de las cantidad mgy al principio y al final del desplazamiento. El producto mgy recibe el nombre de energía potencial gravitatoria . 09/06/09 L Arrascue, H Vizcarra, Y Milachay

3. Energía potencial U La expresión muestra que podemos expresar el trabajo del peso en términos de los valores de las cantidad mgy al principio y al final del desplazamiento. El signo negativo de ∆U implica que: Cuando la energía potencial del cuerpo aumenta, el trabajo realizado por el peso es negativo. Cuando la energía potencial del cuerpo disminuye. El trabajo realizado por el peso es positivo. Energía potencial La energía potencial sólo tiene sentido cuando se establece un nivel de referencia. El nivel de referencia es arbitrario. El valor de la energía potencial depende del nivel de referencia y de la masa del cuerpo. 09/06/09 L Arrascue, H Vizcarra, Y Milachay y-y 0 m w g Nivel de referencia

4. Fuerzas conservativas Fuerzas conservativas y no conservativas Son fuerzas cuyo trabajo realizado sobre una trayectoria cerrada es igual a cero. El trabajo realizado por una fuerza conservativa siempre tiene las siguientes propiedades: Puede expresarse como la diferencia entre los valores inicial y final de una función de energía potencial. Es independiente de la trayectoria del cuerpo y depende solo de los puntos inicial y final. Si los puntos inicial y final son el mismo punto (trayecto cerrado) el trabajo total es nulo. Es reversible. 09/06/09 L Arrascue, H Vizcarra, Y Milachay

5. Energía mecánica E Ejercicio . Desde el piso se lanza un proyectil de 4,00 kg de masa en dirección vertical hacia arriba con una rapidez de 29,43 m/s. a) Escriba las ecuaciones de su movimiento y(t) y v y (t ). b) Calcule y(m ), v y (m/s) , K , U , K+U en t = 0 s, 2,00 s y 4,00 s 09/06/09 L Arrascue, H Vizcarra, Y Milachay Energía mecánica Se define la energía mecánica como la suma de la energía cinética de un cuerpo mas su energía potencial. Si sólo la fuerza de gravedad efectúa trabajo, la energía mecánica total es constante, es decir, se conserva El peso de los cuerpos es una fuerza conservativa t(s) y(m) v y (m/s) K U K+U 0,00 0,00 29,4 1729 0,00 1,73x10 3 2,00 39,2 9,81 192 1538 1,73x10 3 4,00 39,2 -9,81 192 1538 1,73x10 3

6. Conservación de la energía mecánica Si se escribe la expresión del trabajo en función de la energía cinética para el caso de un bloque que se mueve por acción de la gravedad, ésta será igual a: Por otro lado, ese mismo trabajo se escribirá como: Igualando la expresión del trabajo. En el caso de que el aporte en la energía se dé en resortes y por el movimiento en el campo gravitatorio, la expresión general sería: 09/06/09 L Arrascue, H Vizcarra, Y Milachay

7. Energía potencial elástica La fuerza del resorte siempre se opone al movimiento del bloque mostrado ( F R =-kx ) Trabajo realizado por el resorte: 09/06/09 L Arrascue, H Vizcarra, Y Milachay Energía potencial elástica

8. El trabajo total hecho sobre un cuerpo es igual al cambio de su energía cinética Consideremos el trabajo total efectuado sobre el objeto como la suma del trabajo efectuado por el peso más el trabajo realizado por las otras fuerzas aplicadas al objeto. 09/06/09 L Arrascue, H Vizcarra, Y Milachay Conservación de la energía mecánica

9. Analizando la expresión: De la anterior expresión concluimos que: WFNC > 0, entonces la energía mecánica total aumenta. WFNC < 0, entonces la energía mecánica total disminuye. WFNC = 0, entonces la energía mecánica inicial es igual a la energía mecánica final, es decir la energía mecánica total se conserva. Ejercicio . Desde el piso se lanza un proyectil de 4,00 kg de masa en dirección vertical hacia arriba con una rapidez de 29,43 m/s. a) Calcule y(m ), v y (m/s) , K , U , K+U en t = 0 s, 2,00 s y 4,00 s Conservación de la energía mecánica 09/06/09 L Arrascue, H Vizcarra, Y Milachay t(s) y(m) v y (m/s) K U K+U 0,00 0,00 29,4 1729 0,00 1,73x10 3 2,00 39,2 9,81 192 1538 1,73x10 3 4,00 39,2 -9,81 192 1538 1,73x10 3

10. En un puesto de carga de camiones en una oficina de correos, un paquete de 0,200 kg de masa se suelta del reposo en el punto A de una vía que forma un cuarto de circulo con radio de 1,60 m . El paquete es tan pequeño relativo a dicho radio que puede tratarse como partícula. El paquete se desliza por la vía y llega al punto B con rapidez de 4,80 m/s . A partir de ahí, el paquete se desliza 3,00 m sobre una superficie horizontal hasta el punto C, donde se detiene. a) ¿Qué coeficiente de fricción cinética tiene la superficie horizontal. b) ¿Cuánto trabajo realiza la fricción sobre el paquete al deslizarse éste por el arco circular entre A y B? Solución: Cualquiera que sea el punto donde se analice al bloque, actuarán sobre él tres fuerzas: peso, normal y la fricción. De estas tres fuerzas, solo el peso es conservativa, la fricción y la normal son fuerzas no conservativas. Aplicamos el teorema de trabajo y energía entre B y C Ejercicio 09/06/09 L Arrascue, H Vizcarra, Y Milachay

11. La vagoneta de una montaña rusa de masa m = 1 500 kg. Parte de un punto situado a una altura H = 23,0 m respecto de la parte mas baja de un riso de 15,0 m de diámetro (ver figura). Si el rozamiento es despreciable. Determinar la fuerza normal debajo de los carriles sobre la vagoneta cuando los pasajeros están cabeza abajo en el punto mas alto del rizo. Ejercicio Solución En el punto mas alto del rizo. Aplicamos el teorema de trabajo y energía entre A y B Luego 09/06/09 L Arrascue, H Vizcarra, Y Milachay

12. Ejercicio Una mujer que pesa 600 N se sube a una báscula que contiene un resorte rígido. En equilibrio, el resorte se comprime 1,0 cm bajo su peso. Calcule la constante del resorte y el trabajo total efectuado sobre él durante la compresión. Solución: Con las coordenadas escogidas, x = -1,0 cm = -0,010 m y la fuerza es F x = -600 N. Entonces: Ahora usando x 1 = 0 y x 2 = -0,010 m, tenemos: Un objeto de 3,00 kg en reposo se deja libre a una altura de 5,00 m sobre una rampa curva y sin rozamiento. Al pie de la rampa hay un muelle cuya constante es k = 400 N/m. El objeto se desliza por la rampa y choca contra el muelle, comprimiéndolo una distancia x antes de alcanzar momentáneamente el reposo. (a) Determinar x (b) Que ocurre con el objeto después de alcanzar el reposo. Solución 09/06/09 L Arrascue, H Vizcarra, Y Milachay

13. Potencia La potencia suministrada por una fuerza es el trabajo realizado por dicha fuerza por unidad de tiempo. La unidad del SI de la potencia es el joule por segundo y se llama watt . La unidad inglesa de la potencia es el cabello de vapor. Un pequeño ascensor eleva una carga de ladrillos de peso 800 N a una altura de 10,0 m en 20,0 s . ¿Cuál es la potencia mínima que debe suministrar el motor? Solución 09/06/09 L Arrascue, H Vizcarra, Y Milachay

14. Una caja de masa M se encuentra en la parte mas baja de un plano inclinado sin rozamiento. La caja esta atada a un cuerda que tira de ella con una tensión constante T (a) Determinar el trabajo realizado por la tensión cuando la caja se ha desplazado una distancia x a lo largo del plano. (b) Determinar la velocidad en función de x y  (c) Determina la potencia desarrollada en función de T, x y  Solución (a) W = T x (b) Trabajo neto – Energía cinética (c) Potencia 09/06/09 L Arrascue, H Vizcarra, Y Milachay