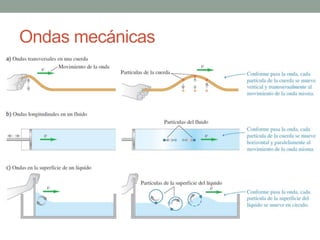
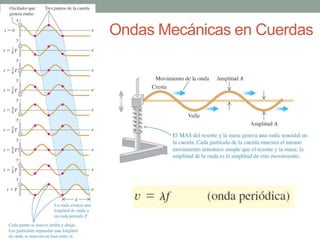
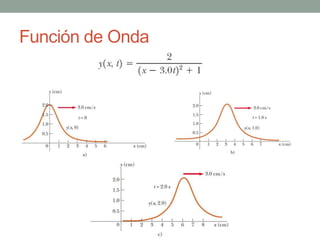
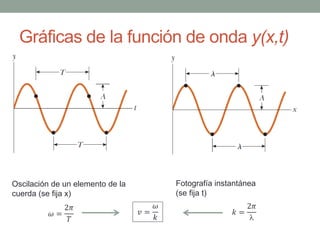
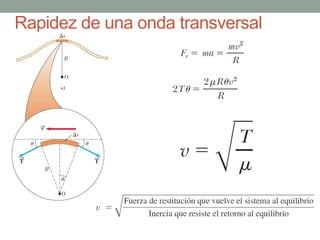
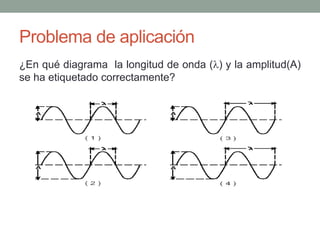
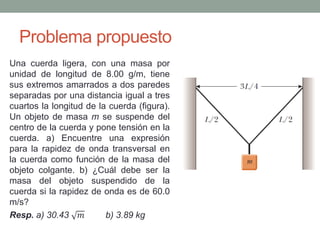
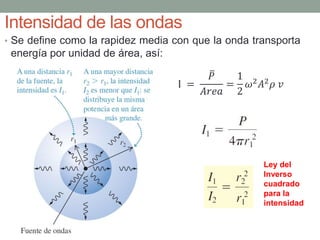
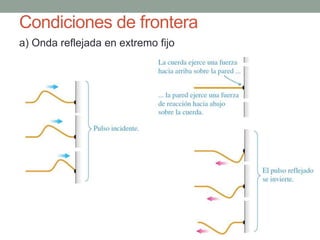
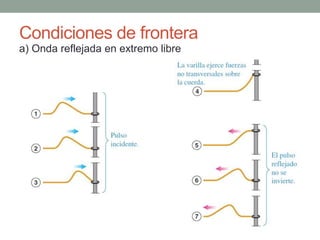
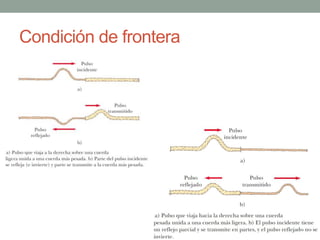
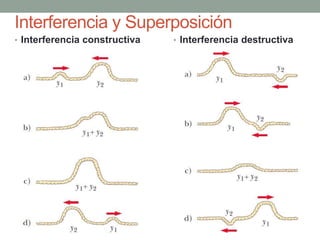
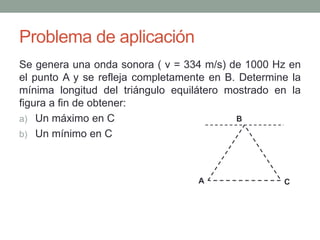
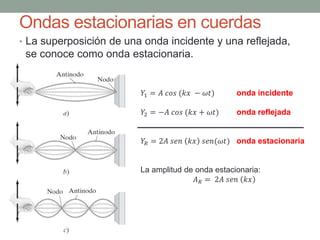
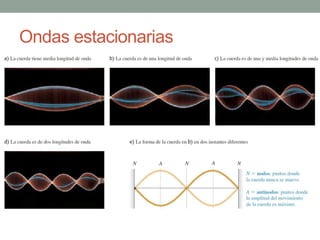
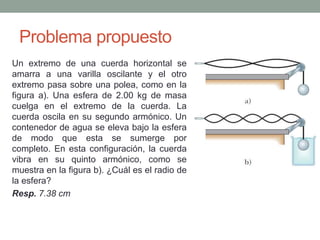
Este documento proporciona una introducción al movimiento ondulatorio y las ondas mecánicas. Explica que las ondas son oscilaciones que van y vienen a través de un medio, y clasifica las ondas en mecánicas y electromagnéticas. Describe las características de las ondas mecánicas en cuerdas y agua, y presenta ecuaciones que describen el movimiento ondulatorio. También cubre conceptos como interferencia de ondas, ondas estacionarias y condiciones de frontera.

1. MOVIMIENTO
ONDULATORIO
Ondas 1
Elaborado por: Ing. Víctor Velasco Galarza

2. Ondas
Todo aquello que:
• Va y viene
• Va de un lado a otro y regresa
• Entra y sale
• Se enciende y apaga
• Es fuerte y débil
• Sube y baja
Todos son vibraciones, es decir oscilaciones en el espacio (x) –
tiempo (t).

3. Ondas
• La luz y el sonido son ejemplos de ondas.
• Las ondas son transporte de energía no de materia.

4. Clasificación de las Ondas
• Ondas Mecánicas: Necesitan de un
medio para su propagación, por tanto
no se propagan en el vacío.
• Ondas en cuerdas
• Ondas en agua
• Ondas sonoras
• Ondas Electromagnéticas: No
necesitan de medio alguno para su
propagación, por tanto se propagan en
el vacío.
• Luz visible
• Radiación solar
• Láser

5. Ondas mecánicas

6. Ondas Mecánicas en Cuerdas

7. Función de una onda
• Toda función con respecto a x y t corresponde a una
función de onda.

8. Función de Onda

9. Función de Onda Armónica
• 𝑦 𝑥, 𝑡 = 𝐴 𝑆𝑒𝑛 𝑘𝑥 ∓ 𝜔𝑡 + 𝜑
ó
• 𝑦 𝑥, 𝑡 = 𝐴 𝐶𝑜𝑠 𝑘𝑥 ∓ 𝜔𝑡 + 𝜑
Número de onda (k): k =
2𝜋

;
  representa a la longitud de onda
Frecuencia angular  =
2𝜋
𝑇
= 2𝜋𝑓 ;
f  frecuencia natural
Constante de fase  en radianes.

10. Gráficas de la función de onda y(x,t)
Fotografía instantánea
(se fija t)
Oscilación de un elemento de la
cuerda (se fija x)
𝑘 =
2𝜋
𝜔 =
2𝜋
𝑇
𝑣 =
𝜔
𝑘

11. Ecuación diferencial parcial de Onda

12. Rapidez de una onda transversal

13. Problema de aplicación
Un vibrador produce una onda en la superficie del agua
cada 0,5 s. Dichas ondas tienen de longitud de onda 3 cm
y su velocidad en cm/s es:
A) 1,5
B) 4,5
C) 3,0
D) 6,0

14. Problema de aplicación
¿En qué diagrama la longitud de onda () y la amplitud(A)
se ha etiquetado correctamente?

15. Problema de aplicación
Cuál es la ecuación de una onda transversal plana de 10
cm de amplitud y de 0.5 s de período que se desplaza a
340 m/s hacia la parte positiva del eje OX, suponiendo que
en el origen y en el instante inicial la elongación es
máxima?
a) y(x,t) = 0,3 sen (3,696 . 10-2 x– 4 t +  /4) m
b) y(x,t) = 0,1 sen (3,696 . 10-2 x –4 t +  /2) m
c) y(x,t) = 0,1 sen (3,696 . 10-3 x –4 t +  /4) m
d) y(x,t) = 0,2 sen (3,696 . 10-2 x –4 t +  /2) m

16. Problemas de aplicación
• El extremo izquierdo de una cuerda estirada en posición
horizontal se hace oscilar transversalmente con MAS de f
= 243 Hz y amplitud 2.60 cm. La cuerda está bajo tensión
de 140 N y tiene densidad lineal  = 0,121 kg/m. Al
tiempo t = 0 se halla que el extremo izquierdo de la
cuerda está desplazado 1.60 cm hacia arriba y
moviéndose hacia arriba. Escriba la función de la onda
y(x,t).
Resp. y(x,t) = 2.60 cos( 44.9 x – 486 t + 0.908 ) cm

17. Problemas de aplicación
• Un alambre no uniforme de densidad lineal  = 0.50x
kg/m, donde x es la distancia de sus extremos, tiene una
longitud total de 2.0 m y una masa de 1.0 kg. Si el
alambre está sometido a una tensión de 40 N, ¿Qué
tiempo le toma a un pulso recorrer este alambre desde un
extremo al otro?
Resp. t = 0.21 s

18. Problema propuesto
Una cuerda ligera, con una masa por
unidad de longitud de 8.00 g/m, tiene
sus extremos amarrados a dos paredes
separadas por una distancia igual a tres
cuartos la longitud de la cuerda (figura).
Un objeto de masa m se suspende del
centro de la cuerda y pone tensión en la
cuerda. a) Encuentre una expresión
para la rapidez de onda transversal en
la cuerda como función de la masa del
objeto colgante. b) ¿Cuál debe ser la
masa del objeto suspendido de la
cuerda si la rapidez de onda es de 60.0
m/s?
Resp. a) 30.43 𝑚 b) 3.89 kg

19. Energía en el movimiento ondulatorio
• Como se aprendió en MAS:
como 𝜔 =
𝑘
𝑚
,  𝑘 = 𝑚𝜔2
y como 𝑚 = 𝜇∆𝐿  𝐸 =
1
2
𝜔2 𝐴2 𝜇(∆𝐿) , así:
• Potencia media: 𝑃 =
𝐸
∆𝑡
=
1
2
𝜔2 𝐴2 𝜇 𝑣
“La rapidez de transferencia de energía en cualquier
onda sinusoidal es proporcional al cuadrado de la
frecuencia angular y al cuadrado de la amplitud”.

20. Intensidad de las ondas
• Se define como la rapidez media con que la onda transporta
energía por unidad de área, así:
I =
𝑃
𝐴𝑟𝑒𝑎
=
1
2
𝜔2 𝐴2 𝜌 𝑣
Ley del
Inverso
cuadrado
para la
intensidad

21. Problemas de aplicación
• En una cuerda de densidad lineal 10 g/cm se propaga
una onda sinusoidal de la forma
y (x,t) = 2.0 sen (5x – 3t – 4 )
con x y y en metros y t en segundos.
a) ¿Cuál es la velocidad (magnitud y dirección) de
propagación de la onda?
b) Calcule la potencia media necesaria para generarla
c) Escriba la función de velocidad de oscilación v(x,t)

22. Problema de aplicación
• Una sirena del sistema de advertencia de tornados que
está colocada en un poste alto genera ondas sonoras
uniformemente en todas direcciones. A una distancia de
15 m la intensidad del sonido es de 0.250 W/m2. ¿A qué
distancia de la sirena la intensidad es de 0.010 W/m2?

23. Condiciones de frontera
a) Onda reflejada en extremo fijo

24. Condiciones de frontera
a) Onda reflejada en extremo libre

25. Condición de frontera

26. Problema de aplicación
• Una cuerda tiene dos secciones con densidades lineales
de 0.10 kg/m y 0.20 kg/m, figura. Una onda incidente,
dada por Y = (0.050 m) sen(7.5x – 12.0t), donde x está en
metros y t en segundos, viaja a lo largo de la cuerda más
ligera. a) ¿Cuál es la longitud de onda sobre la sección
más ligera de la cuerda? b) ¿Cuál es la tensión en la
cuerda? c) ¿Cuál es la longitud de onda cuando la onda
viaja sobre la sección más pesada?

27. Problema propuesto
• Para el problema anterior. ¿Cuál es la amplitud de la
onda transmitida a la parte derecha de la cuerda?
Resp. 0.042 m

28. Interferencia de ondas. Principio de
superposición
• Se denomina interferencia al fenómeno de traslape entre
dos o más ondas viajeras al pasar por la misma región al
mismo tiempo.
• Cuando dos ondas interfieren (se traslapan), el
desplazamiento real de la onda resultante es la suma de
los desplazamientos de cada una de las ondas.
Fenómeno conocido como Principio de superposición.

29. Interferencia y Superposición
• Interferencia constructiva • Interferencia destructiva

30. Identidades de la suma o diferencia de
senos y cosenos

31. Interferencia de fuentes sincronizadas
• Sean:
𝑌1 = 𝐴 𝑠𝑒𝑛 (𝑘𝑥1 − 𝜔𝑡)
𝑌2 = 𝐴 𝑠𝑒𝑛 𝑘𝑥2 − 𝜔𝑡
𝑌𝑅 = 2𝐴 𝑐𝑜𝑠
1
2
𝑘 𝑥1 − 𝑥2 𝑠𝑒𝑛
1
2
𝑘 𝑥1 + 𝑥2 − 𝜔𝑡
Donde la amplitud resultante es 𝐴 𝑅 = 2𝐴 𝑐𝑜𝑠
1
2
𝑘 𝑥1 − 𝑥2
• Interferencia constructiva: ∆𝑥 = 𝑛
𝑛 = 0, ±1, ±2, ±3, . . (múltiplo entero)
• Interferencia destructiva: ∆𝑥 = 𝑛

2
𝑛 = ±1, ±3, ±5, . . (entero impar)

32. Problema de aplicación
Se genera una onda sonora ( v = 334 m/s) de 1000 Hz en
el punto A y se refleja completamente en B. Determine la
mínima longitud del triángulo equilátero mostrado en la
figura a fin de obtener:
a) Un máximo en C
b) Un mínimo en C
A
B
C

33. Problema propuesto
Dos altavoces se excitan por medio de un oscilador común
de 680 Hz y se ponen uno frente al otro a una distancia de
1.30 m. Localice los puntos a los largo de una línea que
una los dos altavoces (entre ellos) donde se esperarían
mínimos relativos. (considere v = 340 m/s)
Resp. x = 0.025 m
x = 0.275 m
x = 0.525 m
x = 0.775 m
x = 1.025 m
x = 1.275 m

34. Interferencia de dos ondas desfasadas
• Sean:
𝑌1 = 𝐴 𝑠𝑒𝑛 (𝑘𝑥 − 𝜔𝑡 + 𝜑1 )
𝑌2 = 𝐴 𝑠𝑒𝑛 (𝑘𝑥 − 𝜔𝑡 + 𝜑2)
𝑌𝑅 = 2𝐴 𝑐𝑜𝑠
1
2
𝜑1 − 𝜑2 𝑠𝑒𝑛
1
2
𝑘𝑥 − 𝜔𝑡
Donde la amplitud resultante es
𝐴 𝑅 = 2𝐴 𝑐𝑜𝑠
1
2
𝜑1 − 𝜑2
• Interferencia constructiva: ∆𝜑 = 𝑛𝜋
𝑛 = 0, ±2, ±4, ±6, . . (entero par)
• Interferencia destructiva: ∆𝜑 = 𝑛𝜋
𝑛 = ±1, ±3, ±5, . . (entero impar)

35. Problema de aplicación
Una onda se propaga en el sentido negativo de las X. Si A = 10
mm, f = 550 Hz y v = 330 m/s. Si en t = 0 y x = 0, Y = 10 mm.
a) Escriba la función de onda.
b) Hallar la diferencia de fase entre dos puntos que se
encuentran, en un instante dado, a una distancia de 2.4 m.
c) Calcular la velocidad máxima de una partícula alcanzada por
la onda.

36. Problema propuesto
Una onda de 493 Hz de frecuencia tiene una velocidad de
353 m/s. ¿Qué distancia están separados dos puntos que
difieren en fase 55°?
Resp. 0.109 m

37. Interferencia por fasores
• Sean:
𝑌1 = 𝐴1 𝑠𝑒𝑛 (𝑘𝑥 − 𝜔𝑡 + 𝜑 1)
𝑌2 = 𝐴2 𝑠𝑒𝑛 (𝑘𝑥 − 𝜔𝑡 + 𝜑 2)
𝑌𝑅 = 𝐴 𝑅 𝑠𝑒𝑛 (𝑘𝑥 − 𝜔𝑡 + 𝛿)
• AR es la magnitud de la resultante de sumar los fasores que
representa cada función de onda.
•  corresponde a la dirección de la resultante de sumar los fasores
que representa cada función de onda.

38. Problema de aplicación
Dos ondas que se propagan en una misma dirección con
una rapidez de 20 m/s, tienen 20 y 30 cm de amplitud,
respectivamente. La longitud de onda es de 4m y la fase
inicial de la primera onda es 20° y de la segunda es de 30°.
Determine:
a) La función de cada onda
b) La función de onda resultante
c) La intensidad de la onda si se conoce que  = 2.7 g/cm3

39. Ondas estacionarias en cuerdas
• La superposición de una onda incidente y una reflejada,
se conoce como onda estacionaria.
𝑌1 = 𝐴 𝑐𝑜𝑠 (𝑘𝑥 − 𝜔𝑡) onda incidente
𝑌2 = −𝐴 𝑐𝑜𝑠 (𝑘𝑥 + 𝜔𝑡) onda reflejada
𝑌𝑅 = 2𝐴 𝑠𝑒𝑛 𝑘𝑥 𝑠𝑒𝑛(𝜔𝑡) onda estacionaria
La amplitud de onda estacionaria:
𝐴 𝑅 = 2𝐴 𝑠𝑒𝑛 𝑘𝑥

40. Ondas estacionarias

41. Frecuencias naturales (serie armónica)

42. Problema de aplicación
La porción de una cuerda de cierto
instrumento musical que está entre el puente
y el extremo superior del batidor (o sea, la
porción que puede vibrar libremente) mide
60.0 cm y tiene una masa de 2.00 g. La
cuerda produce una nota A4 (440 Hz) al
tocarse. a) ¿A qué distancia x del puente
debe una ejecutante poner un dedo para tocar
una nota D5 (587 Hz)? (Vea la figura) En
ambos casos, la cuerda vibra en su modo
fundamental. b) Sin reafinar, ¿es posible tocar
una nota G4 (392 Hz) en esta cuerda? ¿Por
qué?

43. Problema de aplicación
Un alambre de 5.00 m y 0.732 kg se utiliza para sostener dos postes
uniformes de 235 N con igual longitud (figura). Suponga que, en
esencia, el alambre es horizontal y que la rapidez del sonido es de 344
m/s. Está soplando un fuerte viento, lo que provoca que el alambre
vibre en su séptimo sobretono. ¿Cuáles son la frecuencia y la longitud
de onda del sonido que produce el alambre?

44. Problema propuesto
Un extremo de una cuerda horizontal se
amarra a una varilla oscilante y el otro
extremo pasa sobre una polea, como en la
figura a). Una esfera de 2.00 kg de masa
cuelga en el extremo de la cuerda. La
cuerda oscila en su segundo armónico. Un
contenedor de agua se eleva bajo la esfera
de modo que esta se sumerge por
completo. En esta configuración, la cuerda
vibra en su quinto armónico, como se
muestra en la figura b). ¿Cuál es el radio de
la esfera?
Resp. 7.38 cm