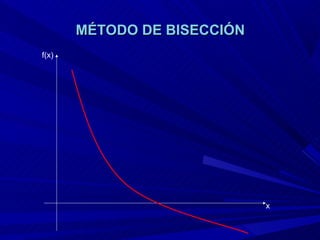
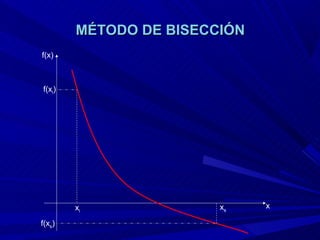
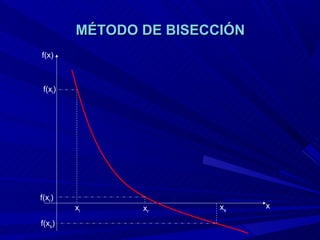
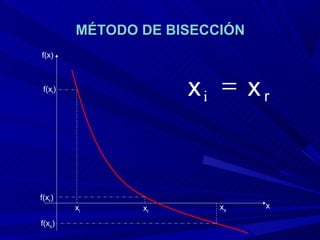
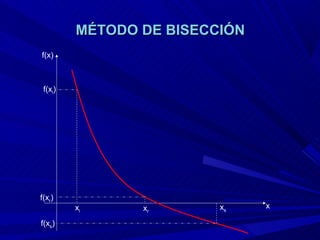
El método de bisección consiste en considerar un intervalo donde la función tiene raíz, bisectar ese intervalo para obtener un punto de aproximación de la raíz, e identificar en qué subintervalo está la raíz real. Este proceso se repite hasta que el punto de bisección coincide con el valor exacto de la raíz.

1. MÉTODOS NUMÉRICOS
Raíces de ecuaciones

2. MÉTODO DE BISECCIÓN
f(x)
x

3. MÉTODO DE BISECCIÓN
Consiste en considerar un intervalo (xi, xs) en el que se
garantice que la función tiene raíz.

4. MÉTODO DE BISECCIÓN
f(x)
f(xi)
xi xs x
f(xs)

5. MÉTODO DE BISECCIÓN
Consiste en considerar un intervalo (xi, xs) en el que se
garantice que la función tiene raíz.
El segmento se bisecta, tomando el punto de bisección
xr como aproximación de la raíz buscada.

6. MÉTODO DE BISECCIÓN
f(x)
f(xi)
f(xr)
xi xr xs x
f(xs)

7. MÉTODO DE BISECCIÓN
Consiste en considerar un intervalo (xi, xs) en el que se
garantice que la función tiene raíz.
El segmento se bisecta, tomando el punto de bisección
xr como aproximación de la raíz buscada.
Se identifica luego en cuál de los dos intervalos está la
raíz.

8. MÉTODO DE BISECCIÓN
f(x)
f(xi) xi = x r
f(xr)
xi xr xs x
f(xs)

9. MÉTODO DE BISECCIÓN
Consiste en considerar un intervalo (xi, xs) en el que se
garantice que la función tiene raíz.
El segmento se bisecta, tomando el punto de bisección
xr como aproximación de la raíz buscada.
Se identifica luego en cuál de los dos intervalos está la
raíz.
El proceso se repite n veces, hasta que el punto de
bisección xr coincide prácticamente con el valor exacto
de la raíz.

10. MÉTODO DE BISECCIÓN
f(x)
f(xi)
f(xr)
xi xr xs x
f(xs)