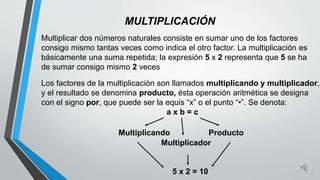
Los números naturales surgieron para contar y ordenar cantidades. Incluyen los números 0, 1, 2, 3, etc. Pueden representarse en una línea numérica y se pueden operar mediante la suma, resta, multiplicación y división. También incluyen conceptos como los números primos, compuestos, múltiplos, divisores, y la resolución de ecuaciones en este conjunto.

1. Números
Naturales

2. ORIGEN
• Los números naturales son los primeros que surgen en las distintas
civilizaciones, ya que las tareas de contar y de ordenar son las más
elementales que se pueden realizar en el tratamiento de las
cantidades.

3. LOS NÚMEROS NATURALES
• El conjunto de los números naturales sin el cero lo vamos a denotar
por N*, así:
N* = { 1, 2, 3, 4, 5, 6, …….. }
• Vamos a denotar con N el conjunto formado por todos los números
naturales, esto es:
N = { 0, 1, 2, 3, 4, 5, 6, ……. }
• Los números naturales 0, 1, 2, 3, 4, 5, …….. Surgen como un recurso
para contar y son infinitos (∞)

4. El número natural que sirve para designar la cantidad de elementos
que tiene cierto conjunto, y se llama cardinal
• Además de cardinales (para contar), los números naturales son
ordinales, pues sirven para ordenar los elementos de un conjunto:

5. Representación grafica del conjunto N
Para representar gráficamente el conjunto de los números naturales,
elegimos una recta orientada como indica la figura:
0 1 2 3 4 5 6 7 ………………… ∞
Se selecciona un punto
arbitrario de la recta
para representar el
cero (0).
Ubicamos otro punto a la derecha del
cero para representar el uno (1).
Al segmento formado entre el
cero (0) y el uno(1), le
llamamos segmento unidad
Luego dividimos toda la recta en segmentos que tengan la misma
longitud que el segmento unidad y a los sucesivos puntos le
corresponden los números 2, 3, 4, 5, ……. Como muestra el gráfico.

6. Operaciones en n
Es una operación de números naturales, que permite
solucionar situaciones en las que se realizan
actividades como agregar, agrupar u ordenar.
ADICIÓN
Así, por ejemplo al par a, b є N se le hace corresponder s є N
mediante la operación “+”. se escribe:
a + b = s
Sumandos Suma
7 + 5 = 12

7. • Elemento neutro: a + 0 = 0 + a
8 + 0 = 0 + 8
En la adición se verifican las siguientes propiedades para
cualquiera que sean a, b, c є N:
• Conmutativa: a + b = b + a
5 + 3 = 3 + 5
• Asociativa: ( a + b ) + c = a + ( b + c )
( 5 + 3 ) + 6 = 3 + (5 + 6 )
PROPIEDADES DE LA ADICIÓN

8. SUSTRACCIÓN Es una operación que consiste en quitar o
separar de un número mayor otro número
menor, para hallar la diferencia entre dos
números. También se conoce con el
nombre de resta.
Dados dos números naturales a y b, siendo a igual o mayor que b,
se obtiene un número d є N y se llama diferencia de a y b. Se
denota:
a – b = d
Minuendo
Sustraendo
Diferencia
9 – 6 = 3

9. MULTIPLICACIÓN
Multiplicar dos números naturales consiste en sumar uno de los factores
consigo mismo tantas veces como indica el otro factor. La multiplicación es
básicamente una suma repetida; la expresión 5 x 2 representa que 5 se ha
de sumar consigo mismo 2 veces
Los factores de la multiplicación son llamados multiplicando y multiplicador,
y el resultado se denomina producto, ésta operación aritmética se designa
con el signo por, que puede ser la equis “x” o el punto “•”. Se denota:
a x b = c
Multiplicando
Multiplicador
Producto
5 x 2 = 10

10. PROPIEDADES DE LA MULTIPLICACIÓN
En la multiplicación se verifican las siguientes propiedades para
cualquiera que sean a, b, c є N:
Conmutativa: El orden de los factores no varía el producto. Ejemplo:
3 x 10 = 10 x 3
30 = 30
Asociativa: El modo de agrupar los factores no varía el resultado.
Ejemplo:
( 3 x 2 ) x 5 = 3 x ( 2 x 5 )
6 x 5 = 3 x 10
30 = 30

11. Elemento neutro: El 1 es el elemento neutro de la multiplicación porque
todo número multiplicado por él da el mismo número. Ejemplo:
5 x 1 = 5
9 x 1 = 9
Propiedad distributiva: La multiplicación de un número por una suma
es igual a la suma de las multiplicaciones de dicho número por cada
uno de los sumandos. Pongamos un ejemplo: 2 x (3 + 5)
2 x ( 3 + 5 ) = 2 x 3 + 2 x 5
2 x 8 = 6 + 10
16 = 16

12. Factor común: Es el proceso inverso a la propiedad distributiva. Si
varios sumandos tienen un factor común, podemos transformar la suma
en producto extrayendo dicho factor. Veamos el ejemplo:
Si tenemos la operación (2 x 7) + (3 x 7), que tiene como factor común
el 7, podríamos transformar esta operación
( 2 x 7 ) + ( 3 x 7 ) = 7 x ( 2 + 3 )
Factor cero: Todo número N multiplicado por el factor cero (0) se tiene
como resultado cero (0). Observemos:
9 x 0 = 0
152 x 0 = 0
Factor común

13. DIVISIÓN
Dividir un número D (dividendo) entre otro d no nulo (divisor), consiste en
hallar otros dos números, c (cociente) y r (residuo) de modo que se
verifique:
D : d = c, r
Existen dos tipos de división:
División exacta: Una división es exacta cuando el resto es cero. Ejemplo:
15 : 5
( 0 ) 3
Es muy importante resaltar que el divisor d debe ser un número distinto
de cero (0)

14. División entera: Una división es entera cuando el resto es distinto de
cero (0). Ejemplo:
17 : 5
(2) 3
Cero dividido entre cualquier número da cero.
0 : 5 = 0
Observemos que en las operaciones en N, tanto la sustracción como la
división son condicionadas, ya que no siempre se pueden restar ni
dividir dos números naturales cualesquiera.

15. NÚMEROS PRIMOS Y COMPUESTOS
Un número primo p es número natural mayor o igual que 2 que
solamente es divisible por 1 y por el mismo p. Esto es, si p = a,b, siendo
a, b є N, entonces a y b sólo pueden tomar los valores de 1 y p.
El conjunto de los números primos es infinito, veamos algunos ejemplos:
 2 es divisible entre 2 y la unidad (1).
 3 es divisible entre 3 y la unidad (1).
 5 es divisible entre 5 y la unidad (1)
Todo número natural que posee mas de dos divisores se denomina
número compuesto. Ejemplo:
D (12) = {1,2,3,4,6,12} D (15) = {1,3,5,15}

16. DESCOMPOSICION DE FACTORES PRIMOS
Todo número natural no nulo, se puede expresar como un producto
de factores primos, que pueden aparecer repetidos. Ejemplo:
Para descomponer el número 300 en un producto de factores
primos, se procede mediante divisiones sucesivas, comenzando
con el menor divisor primo, hasta llegar al cociente igual a 1
En la practica se dispone así:
300 2
150 2
75 3 300 = 2² . 3 . 5²
25 5
5 5
1

17. MULTIPLOS Y DIVISORES EN N
Los múltiplos de un número son todos aquellos que resultan de
multiplicar ese número por otro número cualquiera. Ejemplo:
9 x 2 = 18 9 x 4 = 36
Los números 18 y 36 son múltiplos de 9
Los múltiplos de un número son infinitos, un número es múltiplo de
sí mismo y el cero (0) es múltiplo de cualquier número
Un número es divisible o divisor de otro número cuando el resultado
de la división es exacto, es decir, sin residuo. Ejemplo:
16 : 4 = 4 16 : 8 = 2
Entonces, 4 y 8 son divisores de 16

18. MÁXIMO COMÚN DIVISOR
Dados los números naturales no nulos a y b, el mayor divisor común de
ellos se llama máximo común divisor de a y b, y se denota:
MCD (a,b)
Para calcular el MCD se procede así: MCD (24,36)
 Se descompone los números en sus factores primos y se obtiene:
24 = 2ᶟ . 3 36 = 2² . 3ᶟ
 Se construye el producto formado por los factores primos comunes
tomados en su menor exponente:
MCD (24,36) = 2² . 3 = 12

19. MÍIMO COMÚN MÚLTIPLO
Dados dos números naturales no nulos a y b, su mínimo común múltiplo
es el menor natural positivo que es múltiplo de ambos números, y se
denota:
mcm (a,b)
Para calcular el mcm (24,45), se procede así:
 Se descomponen los números en sus factores primos:
24 = 2ᶟ . 3 45 = 3² . 5
 Se construye el producto formado por los factores primos comunes
y no comunes con su mayor exponente
mcm (24,45) = 2ᶟ . 3² . 5 = 360

20. ECUACIONES EN EL CONJUNTO N
Una ecuación, es una igualdad que sólo es verdadera para determinados
valores de las letras que en ella figuren. Esas letras que tienen valores
especiales se llaman incógnitas y una vez determinados sus valores, se
tendrá la solución de la ecuación. Ejemplo:
4x + 2 = 14
Generalmente las incógnitas se representan por las últimas letras del
alfabeto: x, y, z.
Los miembros de una ecuación lo conforman dos expresiones
algebraicas que están separadas por el signo de la igualdad (=).
En la ecuación: 4x + 2 = 14
Primer Miembro Segundo Miembro

21. Los términos, son cada una de las expresiones que están conectadas
con otra por el signo más (+) o por el signo menos (-), o la expresión
que está sola en uno de los miembros. Ejemplo:
La siguiente ecuación tiene cuatro términos
2x + 3 = 4x - 3
El grado de una ecuación viene dado por el mayor exponente de la
incógnita.
 5x = 80 Es una ecuación de primer grado porque el exponente
de la x es 1.
 4x² + 3x = 22 Es una ecuación de segundo grado porque el
exponente de la x es 2.

22. RESOLUCIÓN DE LA SIGUIENTE ECUACIÓN
4x - 2 = 2x + 4
4x - 2x = 4 + 2 Transponiendo los términos.
2x = 6 Reduciendo términos semejantes.
x = 6 / 2 Despejando la x.
x = 3