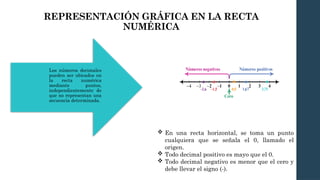
El documento detalla las características y operaciones de los números decimales, su conversión desde fracciones, y la forma de realizar cálculos aritméticos con ellos. También se aborda el sistema métrico decimal y sus unidades de medida, así como la importancia de las cifras significativas y las reglas para redondear resultados. Se incluyen ejercicios prácticos para aplicar los conceptos aprendidos en situaciones cotidianas.

1. NÚMEROS
DECIMALES
Docente: Ing. Marcela Pazmiño N.

2. DEFINICIÓN
Si un automovilista va a
llenar el depósito de
gasolina de su carro y
adquiere 7,12 galones, el
deberá cancelar 10,54
dólares.
El número 10,54 esta
formado por 10 unidades, 5
décimas, y 4 centésimas.
El número que está a la
izquierda de la coma es la
parte entera y el número
que esta a la derecha de la
coma es la parte decimal o
fraccionaria del número
decimal.

3. DEFINICIÓN
Es la expresión en notación decimal de una
fracción, que se obtiene dividiendo el
numerador entre el denominador de una
fracción irreducible.
Un número
decimal consta
de dos partes:
- La parte
entera (que se
separa
mediante una
coma)
Y la parte
decimal

4. REPRESENTACIÓN GRÁFICA EN LA RECTA
NUMÉRICA
Los números decimales
pueden ser ubicados en
la recta numérica
mediante puntos,
independientemente de
que no representan una
secuencia determinada.
 En una recta horizontal, se toma un punto
cualquiera que se señala el 0, llamado el
origen.
 Todo decimal positivo es mayo que el 0.
 Todo decimal negativo es menor que el cero y
debe llevar el signo (-).

5. •1,000000000
decimos
Centésimo
s
Milésimos
Diezmilésimos
Cienmilésimos
Millonésimos
Diezmillonésimos
Cienmillonésimos
Milmillonésimos
Parte
entera

6. EJERCICIOS DE REPASO
• 10,876= diez enteros ochocientos setentena y seis milésimos
• 0,02= cero enteros , dos centésimas
• -5,4= menos cinco enteros cuatro décimos
• 73 13/100= setenta y tres enteros, trece centésimas
• -2 472/1000= menos 2 enteros, cuatrocientos setenta y dos milésimas

7. Conversión de fracciones a números
decimales y viceversa
• Todo número racional tiene dos formas de expresar: como una fracción o
como un número decimal.
• EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES: Como una
fracción es el cociente indicado de dos números, podemos calcular estos
cocientes dividiendo el numerador por el denominador.
• Hallar las expresiones decimales de 7/4, 7/3, y 19/6
7/4=

8. Conversión de fracciones a números
decimales y viceversa
• Cuando el residuo de la división es cero, resulta ser una expresión decimal
limitada, o sea tiene número finito de cifras decimales.
• Cuando el residuo de la división es diferente de cero, resulta ser una
expresión decimal ilimitada. Estos números decimales se caracterizan
porque en ellos aparece un número de cifras llamado período que se repite
indefinidamente.
En el caso de 7/3 se
trata de un número
decimal periódico puro.
En el caso de 19/6 se
trata de un número
decimal periódico mixto.

9. Conversión de fracciones a números
decimales y viceversa

10. EXPRESIÓN FRACCIONARIA DE
LOS NÚMEROS DECIMALES
• Todo número decimal exacto o periódico se puede escribir como una fracción,
llamada fracción generatriz del número decimal.
• Decimal exacto: en el numerador la parte entera seguida de la parte decimal
9,637 = 9637/1000
• Decimal periódico puro: en el numerador el período y en el denominador,
número formado por tantas cifras “9” como cifras tiene el período.
• 3,75757575757575………= 124/33
• Decimal periódico mixto: en el numerador, la parte no periódica seguida
del período, disminuida en la parte no periódica; en el denominador un
número formado por tantas cifras “9” como cifras tiene la parte periódica y
tantos ceros como cifras tiene la parte no periódica.

11. OPERACIONES CON NÚMEROS
DECIMALES
• Para sumar dos números decimales se sigue el siguiente procedimiento:
• Se sitúan los decimales para que se alineen respecto a la coma decimal.
• Después se suma o resta como con los números enteros.
• Al llegar al lugar de la coma escribe una coma en el resultado
• Si uno de los números tiene menos cifras que otro, se aumentarán los ceros
que se requieran para que los dos números tengan el mismo número de
cifras decimales.

12. OPERACIONES CON NÚMEROS
DECIMALES
• Para multiplicar dos números decimales se sigue en siguiente
procedimiento:
• Se multiplican los números como si no tuvieran decimales
• El resultado del producto tendrá tantos decimales como la suma de los
decimales que tenían los números que inicialmente se multiplico.

13. OPERACIONES CON NÚMEROS
DECIMALES
DIVISIÓN DE UN NÚMERO DECIMAL PARA UN ENTERO
- Se efectúa la división de la parte entera de manera usual
- Se baja la cifra correspondiente a las décimas y se coloca una coma en el
cociente.
- Se prosigue la división hasta obtener el número de cifras decimales deseado.
- DIVISIÓN DE UN NÚMERO DECIMAL PARA OTRO DECIMAL
- - Se multiplica el dividendo y el divisor por la unidad seguida de tantos ceros
como cifras decimales tiene el divisor.
- Se realiza la división como se la realizo anteriormente

14. APLICACIONES CON NÚMEROS
DECIMALES
Luego de realizar una actividad deportiva, se sirvió jugo a los asistentes
en vasos de 0,25 litros. Si en total se tiene 3 ½ litros de jugo. ¿Para
cuantos asistentes alcanzo?
Un agricultor cosecho 600 manzanas. Los ¾ de la cosecha las va a
comercializar en un mercado.
-Cuántas manzanas va a comercializar
- El peso promedio de cada manzana es 0,28 kg ¿Cuál es el peso total
que llevará al mercado?
- El kg de manzana esta a $0,62 ¿Cuánto recibirá por la venta?
La pizzería normalmente vende la pizza mediana a $7 la unidad. Los
martes tiene la promoción de 2 pizzas por $10,50.
- Los martes ¿Cuál es el valor de la pizza?
- Cuánto ahorra un cliente que compra la pizza

15. CIFRAS SIGNIFICATIVAS
Las cifras significativas, que también se conocen como dígitos significativos, son las
cifras que contienen la información que resulta de una medición y éstas dependen
directamente del instrumento de medición empleado.
1)Todos los dígitos diferentes de cero son significativos.
2) Los ceros situados entre cifras significativas son significativos.
3) Los ceros a la izquierda del primer dígito diferente de cero, no son significativos.
4) Los ceros situados a la derecha son cifras significativas cuando se escribe el signo
decimal.
5) Si un número no tiene signo decimal y termina con uno o más ceros, dichos ceros
pueden o no ser significativos. Para expresar que son significativos se recurre a escribir el
número en notación científica.
6) Los números escritos en notación científica tienen tantas cifras significativas como
dígitos existan en la cantidad asociada al coeficiente de la potencia base diez de la
expresión.

16. CIFRAS SIGNIFICATIVAS

17. REDONDEO DE UN RESULTADO
• Con frecuencia el resultado que surge de un tratamiento de datos experimentales
contiene un número de cifras mayor que el de las significativas. En este caso, es
necesario redondear tal número a fin de obtener un resultado con el número de
cifras significativas acorde con la medida.
• 1) Redondeo hacia abajo.
Si el dígito siguiente al último lugar retenido es 0, 1, 2, 3 o 4 (seguido o no por otros
dígitos), “consérvese” el valor del dígito situado en el último lugar retenido.
Ejemplos.
• Redondeo a dos cifras significativas.
1.5496 se redondea a 1.5

6.20 se redondea a 6.2


18. REDONDEO DE UN RESULTADO
• Con frecuencia el resultado que surge de un tratamiento de datos experimentales
contiene un número de cifras mayor que el de las significativas. En este caso, es
necesario redondear tal número a fin de obtener un resultado con el número de
cifras significativas acorde con la medida.
• 2) Redondeo hacia arriba.
Si el dígito siguiente al último lugar retenido es 5 (seguido de otros dígitos no todos
cero) o 6, 7, 8 o 9 (seguido o no de otros dígitos), “increméntese” el dígito existente en
el último lugar retenido, en una unidad.
•
Ejemplos. Redondeo a tres cifras significativas.
 49.8501 se redondea a 49.9
27.0864 se redondea a 27.1


19. REDONDEO DE UN RESULTADO
• Con frecuencia el resultado que surge de un tratamiento de datos experimentales contiene un
número de cifras mayor que el de las significativas. En este caso, es necesario redondear tal
número a fin de obtener un resultado con el número de
cifras significativas acorde con la medida.
• 3) Redondeo al valor “par” más próximo.
Cuando el dígito siguiente al último lugar retenido es un 5 y no hay dígitos más allá de ese
número o son solamente ceros, “increméntese” en una unidad el dígito en el último lugar a
ser retenido si es impar, dejando el dígito sin cambio si es par.
Esta regla se aplica también para valores positivos y negativos, considerando el “cero” como
dígito par.
Ejemplos. Redondeo a dos cifras significativas.
 5.85 se redondea a 5.8
2.1500 se redondea a 2.2


20. OPERACIONES CON CIFRAS
SIGNIFICATIVAS
• Suma y resta.
El resultado obtenido mediante la operación suma o resta, debe contener el mismo
número de dígitos después del signo decimal que el sumando que menos contenga.
• Multiplicación y división
• El resultado debe corresponder con el número de cifras significativas de aquel valor que
contenga el menor número de cifras significativas.

21. SISTEMA MÉTRICO DECIMAL
Es el conjunto de medidas que se derivan de un metro. Es un sistema porque
es un conjunto de medidas; métrico, porque su unidad fundamental es el
metro; decimal porque sus medidas aumentan y disminuyen como las
potencias de 10.
CLASE DE MEDIDAS
Existen cinco clases de medidas: de longitud, de superficie, de volumen, de
capacidad y de peso.

22. SISTEMA MÉTRICO DECIMAL
• El Sistema Métrico Decimal es un sistema de unidades en el cual los múltiplos y submúltiplos
de una unidad de medida están relacionadas entre sí por múltiplos o submúltiplos de 10. El
Sistema Métrico Decimal lo utilizamos en la medida de las siguientes magnitudes:
•
• Longitud
• Masa
• Capacidad
• Superficie
• Volumen
• Las unidades de tiempo no son del Sistema Métrico Decimal, ya que están relacionadas entre sí
por múltiplos o submúltiplos de 60.
• El tiempo es una magnitud del Sistema Sexagesimal.
•

23. UNIDADES DE LONGITUD
• La unidad de las medidas de longitud es el metro, que se representa por m.
• Los múltiplos del metro se forman anteponiendo la palabra metro a las
palabras griegas: Deca, Hecto, Kilo, que significan diez, cien, mil, y los
submúltiplos se forman anteponiendo las palabras griegas: deci, centi, y
mili, que significan décima, centésima, y milésima parte.
• Estas medidas aumentan y disminuyen de diez en diez. Los múltiplos y
submúltiplos del metro son:

24. UNIDADES DE SUPERFICIE
• La unidad de las medidas de superficie es el metro cuadrado.
• Aumentan y disminuyen de cien en cien

25. UNIDADES DE VOLUMEN
• La unidad de medidas es el metro cúbico.
• Aumentan y disminuyen de mil en mil.

26. UNIDADES DE CAPACIDAD
• La unidad de medidas es el litro.
• Aumentan y disminuyen de diez en diez.

27. UNIDADES DE PESO
• La unidad de medidas es el gramo.
• Aumentan y disminuyen de diez en diez.

28. EJERCICIOS DE APLICACIÓN
• Las ruedas de un automóvil tienen una circunferencia de 2m.,62 cm .
¿Cuántas vueltas dará cada rueda si el auto recorre una distancia de 2 Km.,
132m., 68 cm.
• Un terreno rectangular de 14 Dm de largo por 8,50 m de ancho se vende a
$7,50 el . ¿Cuánto sería la venta?
• En un montón de ladrillos de 48 . ¿Cuántos ladrillos habrá si cada uno tiene
4 dm de largo, 10 cm de ancho y 6 cm de alto?
• A un comerciante le ofrecen comprarle 8 kg de mantequilla a $0,80 el kg,
pero no acepta y dos días después tiene que vender esa cantidad de
mantequilla a $0,06 el Hg. ¿Cuánto perdió?