El documento presenta un resumen de los números reales, incluyendo conjuntos numéricos como naturales, enteros, racionales e irracionales. Explica las propiedades de cierre, conmutatividad, asociatividad, elementos neutros y operaciones básicas sobre los números reales. También cubre intervalos, ecuaciones y métodos para resolver ecuaciones de segundo grado.

1. UNIVERSIDAD PRIVADA SAN JUAN BAUTISTA FACULTAD DE MEDICINA HUMANA MATEMATICA BASICA CONTENIDO: NUMEROS REALES TOPICOS DE GEOMETRIA ANALITICA RELACIONES Y FUNCIONES TOPICOS DE CALCULO DIFERENCIAL E INTEGRAL 2001

2. EL SISTEMA DE NUMEROS REALES Los Conjuntos Numericos : -El conjunto de Números Naturales: ( N ) N = {1, 2, 3, 4 ...} El conjunto de Números Enteros ( Z ) Z = {...., -3, -2, -1, 0, 1, 2, 3, ....} El conjunto de Números Racionales ( Q ) Q = { x / x = a / b ; a, b  Z ; b  0 ...} Nota: Un número racional resulta de dividir 2 números enteros. (decimal exacto, decimal inexacto)

3. El conjunto de Numeros Irracionales (Q’) Q’ = {....  2, ..  3,....  ,...  ,....} NOTA : Son los números que no tienen periodicidad en sus cifra decimales Ejem:  2 = 1,4142... e = 2.71828182.......  = 3.141596.. El Conjunto de los Numeros Reales (r) R= Q  Q’ R está representado gráficamente por la recta real -  10 - 3 / 2 ½  2  -  -4 -3 -2 -1 0 1 2 3  EL SISTEMA DE NUMEROS REALES

4. GRAFICA CONJUNTISTA R Q Z N Q’

5. EL SISTEMA DE LOS NUMEROS REALES Se llama el Sistema de Números Reales, a un conjunto no vacío R, dotado de 2 operaciones internas, la adición y la multiplicación, y se denota así: < R , + ,  > donde se considera una relación de orden mayor denotado por “ > ” que satisface los siguientes axiomas:

6. EL SISTEMA DE LOS NUMEROS REALES Axiomas de Adición A.1. Si a,b  R  (a + b )  R ................... ..... Clausura. A.2. a + b = b + a  a,b  R .........................Conmutativa. A.3. (a + b) + c = a + (b + c ) ;  a,b,c  R ................ Asociativa. A.4. Existe 0  R / a + 0 = 0 + a= a ;  a  R .........Elemento neutro aditivo. A.5.  a  R ;  (-a)  R / a + (-a) = (-a) + a = 0 ........... Inverso aditivo. Axiomas de Multiplicación M.1. Si a,b  R  a.b  R ........................ Clausura. M.2. a.b = b.a ;  a,b  R ........................ Conmutativa M.3. (a.b).c = a.(b.c) ;  a,b  R ........................ Asociativa M4.  1  R / 1.a = a.1 =a ;  a  R ....................... Elemento neutro mult. M.5.  a  R , con a  o ,  a -1  R / a -1 .a = a.a -1 =1 ..... Inv. Mult.

7. Axiomas Distributivas respecto a la adición D.1. Si a,b,c  R  a.( b + c) = a.b + a.c ......... Distributiva por la izquierda. D.2. Si a,b,c  R  ( b + c).a = b.a + c.a ....... Distributiva por la derecha. Axiomas de Igualdad. I.1. a = a .................. . (Reflexiva) I.2. Para a,b  R  a = b ó a  b ................. ( Dicotomía ) I.3. Si a = b  b = a ....................( Simetría ) I.4. Si a = b  b = c  a = c .................... ( Transitiva ) I.5. Si a = b  a + c = b + c ;  c  R ............( Unicidad de adición ) I.6. Si a = b  a.c = b.c ;  c  R .............( Unicidad de la multiplicación) EL SISTEMA DE LOS NUMEROS REALES

8. Axioma de Orden O.1. Si a,b  R  a = b ; a > b ; a < b ..............( Tricotomía ) O.2. Si a > b  b > c  a > c .............. ( Transitiva ) O.3. Si a > b  a + c > b + c ;  c  R ..............(Consistencia Aditiva ) O.4. a > b  c > 0  a.c > b.c ............... ( Consistencia Multiplicativa ) O.5. a > b  c < 0  a.c < b.c ............... ( Consistencia Multiplicativa ) Axioma del Supremo: Este axioma nos garantiza que los números Reales incluyen números Racionales Q y que se puede establecer una correspondencia biunívoca entre los puntos de una recta y los números Reales. EL SISTEMA DE LOS NUMEROS REALES

9. EL SISTEMA DE LOS NUMEROS REALES Definición de sustracción de Números Reales Dado dos números a y b . Se define la diferencia de a y b , como la suma de a con el inverso aditivo de b . Es decir : a - b = a + ( - b )  a , b  R Definición de División de Números Reales Dado dos números a y b . Se define el cociente de a entre b , como el producto de a con el inverso multiplicativo de b . Es decir :

10. EL SISTEMA DE LOS NUMEROS REALES TEOREMAS SOBRE ADICIÓN Y MULTIPLICACION

11. EL SISTEMA DE LOS NUMEROS REALES TEOREMAS SOBRE ADICIÓN Y MULTIPLICACION

12. EL SISTEMA DE LOS NUMEROS REALES TEOREMAS SOBRE ADICIÓN Y MULTIPLICACION

13. Son conjuntos de números reales que están definidos mediante la condición de que sus elementos satisfacen ciertas desigualdades. Entre estas tenemos: 1) Intervalo Abierto: Dado a, b  R  {x  R / a < x < b} = < a, b > -  a b  2) Intervalo cerrado: Dado a, b  R  {x  R / a  x  b} = [ a, b ] -  a b  LOS INTERVALOS

14. 3) Intervalos Semiabiertos: i) Dado a, b  R  {x  R / a < x < b} = [ a, b > ii) Dado a, b  R  {x  R / a < x < b} = < a, b ] 4) Intervalos Infintos: i) Dado a  R  {x  R / x > a} = [a, +  > +  b b a a a LOS INTERVALOS

15. ii) Dado a  R  {x  R / x > a} = <a, +  > iii) Dado a  R  {x  R / x < a} = < -  ,a ] iv) Dado a  R  {x  R / x < a} = < -  ,a > -  a -  a +  a LOS INTERVALOS

16. OPERACIONES CON INTERVALOS CONCEPTOS BÁSICOS DE OPERACIONES DE CONJUNTOS 1. Reunión de Conjuntos A  B , es el conjunto de elementos que pertenecen a A ó B ó a ambos. A  B = { x/ x  A  x  B } A B U

17. OPERACIONES CON INTERVALOS 2. Intersección de Conjuntos A  B , es el conjunto de elementos que pertenecen a A y B a la vez, es decir son elementos comunes a ambos conjuntos. A  B = { x/ x  A  x  B } A B U A  B

18. OPERACIONES CON INTERVALOS 3. Diferencia de Conjuntos A - B , es el conjunto de elementos de A que no pertenecen a B. A - B = { x/ x  A  x  B } A B U A -B

19. OPERACIONES CON INTERVALOS 4. Complemento de un Conjunto A  , Es el conjunto de elementos que no pertenecen al conjunto A. A  = { x/ x  U  x  A } A  U A

20. OPERACIONES CON INTERVALOS 3. Diferencia Simétrica de Conjuntos A  B = { x/ x  (A - B )  x  (B - A ) } A  B = ( A - B)  (B - A) A  B = ( A  B) - (B  A) A B U A  B

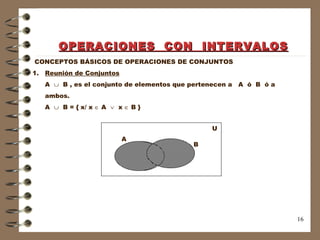
21. OPERACIONES CON INTERVALOS Ejemplos: Dados los intervalos A = <-2 , 2> ; B = [ 0 , 5> ; C = [2 , 7] ; U = R a. A  B b. B  A c. A - B d. A  e. (A  C) - B f. ( A   B)  C Solución -2 0 2 5 A B -2 0 2 5 A B

22. OPERACIONES CON INTERVALOS Ejemplos: Dados los intervalos A = <-2 , 2> ; B = [ 0 , 5> ; C = [2 , 7] ; U = R a. A  B b. B  A c. A - B d. A  e. (A  C) - B f. ( A   B)  C Solución -2 0 2 5 A B -2 0 2 5 A A  A 

23. OPERACIONES CON INTERVALOS Ejemplos: Dados los intervalos A = <-2 , 2> ; B = [ 0 , 5> ; C = [2 , 7] ; U = R a. A  B b. B  A c. A - B d. A  e. (A  C) - B f. ( A   B)  C Solución -2 0 2 5 A B -2 0 2 5 B A 7 C 7 C

24. OPERACIONES CON INTERVALOS Ejemplos: Dados los intervalos A = <-2 , 2> ; B = [ 0 , 5> ; C = [2 , 7] ; U = R a. A  B b. B  A c. A - B d. A  e. (A  C) - B f. ( A   B)  C Solución -2 0 2 5 A  B C 7 A 

25. ECUACIONES E INECUACIONES Una Ecuación es una igualdad que es válida solo para algunos valores. * Una ecuación Lineal (De primer grado ) se expresa en la forma: * Una ecuación cuadrática ( De segundo grado) se expresa en la forma: Es necesario tener en cuenta las siguientes Reglas: 1.- Si se suma o resta una misma expresión a ambos miembros de una ecuación, la ecuación resultante es equivalente a la dada. 2.- Si a ambos miembros de una ecuación se multiplica o se divide entre un numero diferente a cero, la ecuación no varia. ax + b =0 ; a  0 ax 2 + bx + c = 0 ; a  0

26. RESOLUCIÓN DE ECUACIONES DE 2 do GRADO Sea la Ecuación: Para su resolución se utilizará los siguientes métodos: 1.- MÉTODO DE LA FORMULA GENERAL Donde b 2 - 4ac se llama discriminante. - Si b 2 - 4ac > 0 ; la ecuación tiene 2 raíces reales y diferentes - Si b 2 - 4ac = 0 ; la ecuación tiene 2 raíces iguales. - Si b 2 - 4ac < 0 ; la ecuación tiene 2 raíces imaginarias. ax 2 + bx + c = 0 ax 2 + bx + c = 0

27. RESOLUCIÓN DE ECUACIONES DE 2 do GRADO 2.- MÉTODO DE FACTORIZACION: Sea la ecuación: Para su resolución usar el Teorema: ab = 0  a = 0 ó b = 0 3.- MÉTODO DE COMPLETAR CUADRADOS: Sea la ecuación ax 2 + bx + c = 0 Para su resolución usar el Teorema: a 2 = b 2  a = b ó a = - b PROPIEDADES DE LAS RAÍCES DE UNA ECUACIÓN CUADRÁTICA Sea la ecuación: Si sus Raíces son : x 1 y x 2 ; entonces se tiene que: i ) x 1 + x 2 = ; x 1 . x 2 = ii) ( x - x 1 ) ( x - x 2 ) = 0 ax 2 + bx + c = 0 ax 2 + bx + c = 0

28. RESOLUCIÓN DE ECUACIONES DE 2 do GRADO Ejemplo 1 : Dada la ecuación x 2 - 6x + 8 = 0 resolver por los tres métodos. 1.- MÉTODO DE LA FORMULA GENERAL ax 2 + bx + c = 0

29. RESOLUCIÓN DE ECUACIONES DE 2 do GRADO 2.- MÉTODO DE FACTORIZACION: x 2 - 6x + 8 = 0  ( x - 2) (x - 4) = 0 Aplicamos el teorema a.b = 0  a = 0  b = 0 x - 2 = 0  x - 4 = 0  x = 2  x = 4 3.- MÉTODO DE COMPLETAR CUADRADOS: Sea la ecuación ax 2 + bx + c = 0 Para su resolución usar el Teorema: a 2 = b 2  a =b ó a = - b

30. INECUACIONES Una Inecuación es toda desigualdad donde existen una o mas cantidades desconocidas llamadas variables. Las inecuaciones de una variable son proposiciones de la forma: P(x) > 0 , P(x) < 0 , P(x)  0 , P(x)  0 TEOREMAS 1. Si a < b  c < d  a + c < b + d 2. Si a < b  - a > - b 3. Si a < b  c > 0  a . c < b . C 4. Si a < b  c < 0  a . c > b . C 5. Si a  0  a 2 > 0 6. a -1 tiene el mismo signo que a es decir : i. a > 0  a -1 > 0 ii. a < 0  a -1 < 0 7. Si a y b tienen el mismo signo y si : a < b  a -1 > b -1 8. Si a.b > 0  ( a > 0  b > 0 )  ( a < 0  b < 0 ) 9. Si a.b < 0  ( a > 0  b < 0 )  ( a < 0  b > 0 )

31. INECUACIONES 10. Si , b  0  ( a > 0  b > 0 )  ( a < 0  b < 0 ) 11. Si , b  0  ( a > 0  b < 0 )  ( a < 0  b > 0 ) 12. Si a  0  b  0  a 2 > b 2  a > b 13. Si b  0 ; a 2 < b  14. Si b  0 ; a 2 > b  15. Si b > 1  b X < b Y  x < y 16. Si 0 < b < 1  b X < b Y  x> y

32. INECUACIONES 1. INECUACIÓN LIEAL. Es de la forma : * Una Inecuación se caracteriza porque tiene n soluciones. * Para la resolución de una Inecuación lineal es necesario tener en cuenta los siguientes Teoremas: i) Si a > b donde c  R  a + c > b + c ii) Si a > b ; y c > 0  a . c > b . c III) Si a > b ; y c < 0  a . c < b . c Ejemplo: Resolver : 2x - 9 > 5x -3 2x - 9 -5x + 9 > 5x - 3 -5x + 9 -3x > 6  x < -2  S = { x  R / x < -2 }  S=< -  , -2> ax + b > 0 ; ax + b  0 ; ax + b < 0 ; ax + b < 0 -2 - 

33. INECUACIONES 2. INECUACIONES DE SEGUNDO GRADO Es de la forma: Ó donde a , b, c son números reales, a  0 Para la resolución, consideramos los siguientes Teoremas : i ) Si utilizamos el método de Factorización: Si: a . b > 0  ( a > 0  b > 0 )  ( a < 0  b < 0 ) Si: a . b < 0  ( a > 0  b < 0 )  ( a < 0  b > 0 ) Se utiliza los mismos Teoremas para > ó < ii ) Si utilizamos el método completar cuadrados: Si: b > 0  a 2 > b  a <  a > Si: b > 0  a 2 < b  a >  a < es decir: - < a < ax 2 + bx +c > 0 ax 2 + bx +c < 0

34. INECUACIONES Ejemplo. Resolver x 2 - x - 6 > 0 por el método de factorización. Se usará el teorema: a.b > 0  (a>0  b > 0 )  ( a <0  b <0 ) -2 3

35. INECUACIONES Ejemplo. Resolver 3x 2 -2 x - 5 < 0 por el método de Completar cuadrados. Se usará el teorema: a 2 < b  -1 5/3

36. MÉTODO DE LOS VALORES CRÍTICOS 3. INECUACIONES POLINÓMICAS: Son de la forma: P(x) = a 0 + a 1 x + a 2 x 2 + . . . + a n x n > 0 El método que facilita la solución de las inecuaciones polinómicas es el método de los valores críticos. Pasos a seguir: - Se halla los valores críticos factorizando el polinomio P(x) - se ubica los valores críticos en la recta. - se determinan los signos de los intervalos de variación. - La solución será la unión de los intervalos positivos si P(x) > 0 y negativo si P(x) < 0 . Sea el polinomio P(x) = a 0 + a 1 x + a 2 x 2 + . . . + a n x n > 0 d onde P(x) puede factorizarse tal como: P(x) = ( x - r 1 ) ( x - r 2 ) . . . ( x - r n ) entonces se presentan los siguientes casos:

37. MÉTODO DE LOS VALORES CRÍTICOS PRIMER CASO: Cuando las raíces de la ecuación polinómica P(x) = 0 , son reales y diferentes, es decir: i. Si P(x) > 0 o sea P(x) = ( x - r 1 ) ( x - r 2 ) . . . ( x - r n )> 0 Donde : r 1 , r 2 , r 3, . . . r n son los valores críticos, que ordenados en la recta numérica quedan distribuidos así: La solución en este caso es la reunión de los intervalos con signo positivo. Ejemplo: Sea P(x) = x 3 - 5x 2 - 2x + 24 > 0 , Hallar el conjunto solución. -  r 1 r 2 . . . r n -1 r n +  + - + + - + + + - - -2 3 4

38. MÉTODO DE LOS VALORES CRÍTICOS ii. Si P(x) < 0 o sea P(x) = ( x - r 1 ) ( x - r 2 ) . . . ( x - r n )< 0 Donde : r 1 , r 2 , r 3, . . . r n son los valores críticos, que ordenados en la recta numérica quedan distribuidos así: La solución en este caso es la reunión de los intervalos con signo negativo. Ejemplo: Sea P(x) = x 4 + 2x 3 - 9x 2 - 2x + 8 < 0 , Hallar el conjunto solución. -  r 1 r 2 . . . r n -1 r n +  + - + + - + - + - + -4 1 2 -1 +

39. MÉTODO DE LOS VALORES CRÍTICOS SEGUNDO CASO : Si alguna de las raíces del polinomio P(x) = 0 son reales de multiplicidad mayor que (1) , se tiene: suponiendo que el factor ( x - r i ) es el factor que se repite m veces, entonces: i. Si m es par , los signos de los intervalos de variación donde figura r i son iguales , es decir no son alterados. Ejemplo: Sea P(x) = x 4 - 4x 3 - 3x 2 + 14x - 8  0 , Hallar el conjunto Solución. - + - + -2 1 4

40. MÉTODO DE LOS VALORES CRÍTICOS ii. Si m es impar, los intervalos de variación contiguos al valor crítico r i tienen signos diferentes. Ejemplo: Sea P(x) = x 5 - 4x 4 + 14x 2 - 17x + 6 < 0 , Hallar el conjunto Solución. + + - - -2 1 3

41. MÉTODO DE LOS VALORES CRÍTICOS TERCER CASO: Cuando algunas de las raíces del polinomio P(x) = 0 no son reales , en este caso a estas raíces no se consideran en la determinación de los intervalos y para dar la solución , se sigue el mismo procedimiento de los casos anteriores. Ejemplo: Sea P(x) = x 5 - 2x 4 - x 3 - 2x 2 - 20x + 24 > 0 , Hallar el conjunto Solución. + + - - -2 1 3 El factor x 2 + 4 = 0 no tiene raíces reales , por lo que x 2 + 4 > 0  x  R ; podemos prescindir de este factor.

42. INECUACIONES POR EL MÉTODO DE LOS VALORES CRÍTICOS 4. INECUACIONES FRACCIONARIAS. Son inecuaciones de la forma: ( ó con > ó < ) Donde Q(x)  0 Al factorizar P(x) y Q(x) , se aplica el mismo criterio anterior, teniendo en cuenta que los valores críticos correspondientes al denominador nunca es cerrado. NOTA.- Si al factorizar el polinomio, uno de los factores esta afectado a un exponente par, el valor crítico que le corresponde no se toma en cuenta , este mismo criterio se aplica si el valor crítico es un número imaginario.

43. MÉTODO DE LOS VALORES CRÍTICOS Ejemplo: Resolver: Solución. + + - - -7 0 2 Multiplicando por (-1) Aplicando Ruffini en el numerador. -5 4 + -

44. VALOR ABSOLUTO El Valor absoluto de un número real x , denotado por IxI , se define así: Ejemplo: l -4 l = - ( -4) = 4 l 5 l = 5 ALGUNAS DE LAS PROPIEDADES MAS IMPORTANTES 1.- l x l = 0  x = 0 2.- l x l = 3.- l x - y l = l y - x l 4.- l xy l = l x l . l y l 5.- l x + y l < l x l + l y l 6.- l x l 2 = x 2 7.- I x I > I y I  I x I 2 > l y l 2  x 2 > y 2

45. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO * Para la resolución de ecuaciones con Valor Absoluto, nos apoyamos en los siguientes teoremas : i ) Si: l x l = l y l  x = y  x = -y ii) Si: l x l = y  y > 0  ( x = y  x = - y ) * Para la resolución de inecuaciones con valor absoluto, nos apoyamos en los siguientes Teoremas: iii ) y > 0 ; l x l > y  x > y  x < - y iv ) y > 0 ; I x I < y  -y < x < y v ) I x I > I y I  x 2 > y 2  x 2 - y 2 > 0 vi ) I x I < I y I  x 2 < y 2  x 2 - y 2 < 0

46. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 1. Resolver: l x - 2 l = 3x - 9 Aplicamos el teorema: l x l = y  y > 0  ( x = y  x = - y ) 3 2 11/4 7/2

47. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 2. Resolver: l11 x +3 l = 5 Aplicamos el teorema: l x l = y  y > 0  ( x = y  x = - y )

48. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 3. Resolver: l5 x -3 l = l7 + 4x l Aplicamos el teorema: l x l = l y l  x = y  x = - y

49. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 4. Resolver: l x + 3 l  3x - 1 Aplicamos el teorema: l x l  y  - y  x  y -1/2 2

50. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 5. Hallar el conjunto solución l3 x - 11 l  9 Aplicamos el teorema: l x l  y  x  y  x  - y 2/3 20/3

51. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 6. Hallar el conjunto solución de: l5 x + 7 l  8x - 3 Aplicamos el teorema: l x l  y  x  y  x  - y -4/13 10/3

52. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 7. Hallar el conjunto solución de: l x 2 -2x -5 |  l x 2 + 4x +1 | Aplicamos el teorema: l x l  l y l  x 2  y 2 -2 -1 1 - + + -

53. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 8. Hallar el conjunto solución de: l l x l -2 | < l x | Aplicamos el teorema: l x l < l y l  x 2  y 2 -1 1

54. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 9. Demostrar que : Si l x - 1 | < 2 

55. SOLUCIÓN DE ECUACIONES E INECUACIONES CON VALOR ABSOLUTO Ejemplos: 10. Hallar el conjunto solución : 0 3 + - + - + + -3 0