Este documento presenta el diseño preliminar de un avión no tripulado de vigilancia marítima. Incluye un estudio aerodinámico del ala, empenaje, fuselaje y hélice. Analiza las actuaciones de despegue, ascenso, crucero, descenso y la misión completa. También cubre la certificación estructural mediante el cálculo de cargas críticas y la modelización de la caja de torsión. Finalmente, presenta conclusiones sobre el diseño de la aeronave.






![´INDICE DE FIGURAS
3.7. Distribuci´on del momento flector a lo largo de la envergadura
para los dos casos de carga estudiados. . . . . . . . . . . . . . 72
3.8. Distribuci´on del momento torsor a lo largo de la envergadura
para los dos casos de carga estudiados. . . . . . . . . . . . . . 73
3.9. Elipse de cargas N-q. La l´ınea azul es la elipse correspondiente
a las cargas m´aximas, el punto verde corresponde al estado
de cargas al deflectar los alerones y el punto rojo al estado de
cargas con el ala limpia. . . . . . . . . . . . . . . . . . . . . . 77
A.1. Forma del perfil FX 63-143. . . . . . . . . . . . . . . . . . . . 83
A.2. Variaci´on del coeficiente de sustentaci´on del perfil FX 63-143
en funci´on del ´angulo de ataque, medido desde la cuerda, para
n´umeros de Reynolds comprendidos entre 0, 3 · 106
y 3 · 106
.
Datos experimentales obtenidos de [1]. . . . . . . . . . . . . . 84
A.3. Polares del perfil FX 63-143 para n´umeros de Reynolds com-
prendidos entre 0, 3 · 106
y 3 · 106
. Datos experimentales obte-
nidos de [1]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
A.4. Coeficiente de momento de cabeceo del perfil FX 63-137 en
funci´on del ´angulo de ataque, medido desde la cuerda, para
Re = 0, 3 · 106
. Datos experimentales obtenidos de [1]. . . . . . 85
A.5. Forma del perfil FX 71-L-150/25. . . . . . . . . . . . . . . . . 86
A.6. Variaci´on del coeficiente de sustentaci´on del perfil FX 71-L-
150/25 en funci´on del ´angulo de ataque y la deflexi´on del
tim´on, para Re = 0, 7 · 106
. Datos experimentales (.....) . . . . 86
A.7. Variaci´on del coeficiente de sustentaci´on del perfil FX 71-L-
150/25 en funci´on del ´angulo de ataque y la deflexi´on del
tim´on, para Re = 1 · 106
. Datos experimentales (.....) . . . . . 87
A.8. Variaci´on del coeficiente de sustentaci´on del perfil FX 71-L-
150/25 en funci´on del ´angulo de ataque y la deflexi´on del
tim´on, para Re = 1, 5 · 106
. Datos experimentales (.....) . . . . 87
A.9. Variaci´on del coeficiente de sustentaci´on del perfil FX 71-L-
150/25 en funci´on del ´angulo de ataque y la deflexi´on del
tim´on, para Re = 2 · 106
. Datos experimentales (.....) . . . . . 88
A.10.Polar del perfil FX 71-L-150/25 en funci´on de la deflexi´on del
tim´on, para Re = 0, 7 · 106
. Datos experimentales (.....) . . . . 88
A.11.Polar del perfil FX 71-L-150/25 en funci´on de la deflexi´on del
tim´on, para Re = 1 · 106
. Datos experimentales (.....) . . . . . 89
A.12.Polar del perfil FX 71-L-150/25 en funci´on de la deflexi´on del
tim´on, para Re = 1, 5 · 106
. Datos experimentales (.....) . . . . 89
A.13.Polar del perfil FX 71-L-150/25 en funci´on de la deflexi´on del
tim´on, para Re = 2 · 106
. Datos experimentales (.....) . . . . . 90
5](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-7-320.jpg)




![1.1. AERODIN´AMICA DEL ALA
Perfil CLmax Emedia
FX-66-S-96 1,47 77
FX 61-184 1,37 83
FX 63-143 1,41 93
FX 38-153 1,51 85
FX 60-157 1,62 86
Tabla 1.1: clmax y eficiencia aerodin´amica media de los perfiles considerados.
Re=2 · 106.
seleccionado deber´a tener al menos un CLmax = 1,20. Este coeficiente de
sustentaci´on m´aximo depender´a del n´umero de Reynolds de vuelo, que en
crucero es igual a:
Re =
U∞ · ¯c · ρ
µ
=
50 · 0, 94 · 0, 785
167 · 10−7
= 2, 2 · 106
Dado que es recomendable tener digitalizados las caracter´ısticas del perfil
que se seleccione, s´olo se ha buscado posibles perfiles en cat´alogos digitaliza-
dos. En la ETSIA existen varios cat´alogos, de los cuales el ´unico digitalizado
es [1], por lo que se buscar´a en ´este perfiles con car´acter´ısticas adecuadas
para la aeronave del proyecto. En la Tabla 1.1 se recogen las principales
caracter´ısticas de los perfiles considerados, CLmax al n´umero de Re calculado
y eficiencia aerodin´amica para CLmedio
. A la vista de las caracter´ısticas de
cada un de los perfiles se ha escogido el perfil FX 63-143 por ser el que
mayor eficiencia aerodin´amica con un coeficiente de sustentaci´on m´aximo
suficiente, mostrando adem´as una entrada en p´erdida suave.
1.1.2. Distribuci´on de circulaci´on y cl en configuraci´on
limpia.
Para calcular la distribuci´on de circulaci´on adimensional del ala se em-
plear´a el programa weisssg, proporcionado por la c´atedra, que aplica el m´eto-
do de Weissenger detallado en [2]. En el programa es necesario introducir la
forma en planta del ala, as´ı como las dimensiones y situaci´on de los flaps y los
alerones. El resultado es una matriz Q que se relaciona con la circulaci´on
adimensional, G, de forma que:
G(y) =
4Γ(y)
bU∞
= clα Q α
10](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-12-320.jpg)

![1.1. AERODIN´AMICA DEL ALA
En la Figura 1.2 se ha representado la distribuci´on de cl a lo largo de
la envergadura para ´angulos de ataque comprendidos entre los 10 y los
14o
. Las curvas se ha cortado al alcanzar el coeficiente de sustentaci´on
m´aximo, que es menor al variar la cuerda del ala, ya que el n´umero de
Re disminuye. Como se puede apreciar, la primera zona que alcanza el
clmax es la situada al 70 % de la envergadura, lugar en el que se sit´ua el aler´on.
Por todo lo anterior, es recomendable torsionar el ala para disminuir el ´angulo
de ataque a lo largo del ala y provocar que la entrada en p´erdida se produjese
cerca de la ra´ız. Los criterios para la selecci´on de la torsi´on que se proponen
en [3]:
El primer punto donde se inicie la entrada en p´erdida debe estar lo
suficientemente cercano a la ra´ız, siendo el punto m´as adecuado el si-
tuado al 40 % de la semienvergadura. Se debe intentar evitar que la
entrada en p´erdida se produzca en un punto de la envergadura cuya
estela incida en el estabilizador horizontal, ya que podr´ıa conllevar a la
p´erdida de potencia longitudinal.
La entrada en p´erdida debe ser m´as r´apida hacia el interior del ala.
El margen en el coeficiente de sustentaci´on en la secci´on situada al 70 %
de la semienvergadura debe ser de al menos 0,1.
Debido al estrechamiento del ala al 40 % de la semienvergadura, s´olo se
podr´ıa conseguir la entrada en p´erdida en este punto con una torsi´on positiva
en el primer tramo y otra negativa en el segundo, aunque ambas son tan
acusadas que resultan prohibitivas. Aun con esta soluci´on, la entrada en
p´erdida se producir´ıa al 30 % de la semienvergadura, por lo que la estela
incidir´ıa en el estabilizador horizontal, por lo que no ser´ıa una soluci´on
ideal. Por lo tanto, existen dos posibilidades, o bien no se aplica torsi´on y el
punto de entrada en p´erdida estar´ıa situado al 70 % de la semienvergadura,
perdiendo potencia de control lateral, o bien se aplica una torsi´on negativa
y la entrada en p´erdida se produce en la ra´ız, afectando al tim´on de
profundidad. Como ´este ´ultimo tiene una envergadura mayor (el 40 % de
la semienvergadura) y en principio la p´erdida de potencia en el tim´on de
profundidad ser´a menos cr´ıtico se a elegido la ´ultima opci´on, suponiendo
siempre que es la opci´on menos mala. Tomando una torsi´on θ = 0, 8 o
/m, la
entrada en p´erdida se produce en primer lugar en la ra´ız del ala y progresa
hacia el exterior. Debido a la disminuci´on de cuerda, al aumentar el ´angulo
de ataque acaba entrando en p´erdida tambi´en la secci´on situada algo antes
del 70 % de la semienvergadura cuando el primer 30 % ya ha entrado en
12](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-14-320.jpg)




![1.1. AERODIN´AMICA DEL ALA
−0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
CL
w
CD
w
Re=1,5⋅106
Re=2⋅106
Re=2,5⋅106
Figura 1.6: Polar del ala para distintos n´umeros de Reynolds en la ra´ız.
Las curvas experimentales de los perfiles proporcionan la resistencia de fric-
ci´on y de forma, pero no la resistencia inducida del ala debido a que esta
es finita. Este ´ultimo t´ermino puede ser determinado mediante la siguiente
relaci´on (como se indica en [4]):
CDi
=
πΛ
64
∞
n=1
nA2
n (1.3)
En la Figura 1.6 se ha representado la polar del ala para distintos n´umeros
de Reynolds referidos a la ra´ız del ala. N´otese que pr´acticamente no hay
diferencia entre las curvas a distintos n´umeros de Reynolds, debido a que la
resistencia inducida es la predominante a partir de un valor apreciable de CL.
A partir de ahora se tomar´a s´olo se tomar´a las caracter´ısticas aerodin´amicas
correspondientes a un n´umero de Re de 1,5·106
por ser el m´as restrictivo
que se da en la operaci´on normal de la aeronave.
Para calcular el momento aerodin´amico del ala se va a tener en cuenta que
el coeficiente de momento aerodin´amico de cabeceo, cMacw es pr´acticamen-
te constante y que el centro aerodin´amico est´a situado a c/4 del borde de
ataque. Como se puede ver en la Figura 1.7, el coeficiente de momento de
cabeceo del perfil entre los ´angulos de ataque de operaci´on, entre 0 y 8o
apro-
ximadamente, no var´ıa en exceso. Sabiendo que los centros aerodin´amicos de
los perfiles est´an alineados y situados a c/4 del borde de ataque, el coeficiente
17](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-19-320.jpg)

![1.1. AERODIN´AMICA DEL ALA
Aumentar el tama˜no de los flaps hasta que fuesen suficientes para
alcanzar el CLmax requerido. Esta soluci´on tiene el inconveniente de
que habr´ıa que disminuir el tama˜no de los alerones, perdiendo potencia
de mando lateral.
Emplear los alerones como flaps en el aterrizaje. Se perder´ıa potencia
de mando lateral al deflectarlos.
Debido a la sencillez de c´alculo y a que en principio el tama˜no de los ale-
rones ser´a suficiente, la soluci´on finalmente escogida fue la segunda, de ma-
nera que los alerones ocupar´ıan un 25 % de la envergadura. Posteriormente
se calcular´a la potencia de control lateral para comprobar que los alerones
son suficientemente grandes. Los flaps tendr´an las siguientes caracter´ısticas
geom´etricas:
ηi1 = 0, 06
ηe2 = 0, 38
ηi2 = 0, 4
ηe2 = 0, 75
cf /c = 0, 30
Sf /S = 0, 74
Para calcular la variaci´on de la curva de sustentaci´on de los perfiles con
flap se har´a uso del programa proporcionado por la c´atedra que aplica el
m´etodo de weissenger. ´Este da la distribuci´on de circulaci´on si el producto
de la efectividad del mando por la deflexi´on es igual a la unidad, por lo que
para obtener la distribuci´on real habr´a que multipilicarla por la efectividad
del mando y la deflexi´on. Esta distribuci´on se sumar´a a la del ala limpia,
obteniendose la circulaci´on total. La efectividad del mando, τδ, depende
de la deflexi´on del flap, δf , y de la relaci´on cf /c. En la siguiente tabla se
ha recogido estos incrementos en funci´on del ´angulo de deflexi´on del flap,
obtenidos de [5]. Para deflexiones peque˜nas de flap, se consiguen aumentos
significativos del cl, pero para valores entorno a 35o
la efectividad del
mando baja r´apidamente, haciendo que se alcance un m´aximo a los 45o
y
posteriormente acabe disminuyendo.
Por ´ultimo, el incremento m´aximo de sustentaci´on puede expresarse como:
∆clmax = K1K2K3(∆clmax )base (1.4)
Los tres primeros factores, K1, K2 y K3, tienen en cuenta respectivamente
la cuerda del flap, la diferencia de deflexi´on del flap respecto a un ´angulo
19](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-21-320.jpg)





![1.1. AERODIN´AMICA DEL ALA
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
η
G
δa
=10º
δa
=20º
δa
=30º
δa
=40º
Figura 1.13: Distribuci´on de circulaci´on adimensional en el ala debido a la de-
flexi´on del aler´on, para distintos ´angulos de deflexi´on.
1.1.4. Control lateral.
Debido a que ha sido necesario aumentar el tama˜no de los flaps y disminuir
el de los alerones para satisfacer los requerimientos fijados, ser´ıa conveniente
comprobar que la potencia de control lateral es suficiente. Se define como:
Clδa =
∂Cl
∂δa
=
1
qSb
∂L
∂δa
(1.8)
Para calcular el momento de balance debido a la deflexi´on del aler´on se
emplear´a el programa weisssg proporcionado por la escuela, el cual calcula
la distribuci´on de sustentaci´on a lo largo de la envergadura para τaδa = 1,
donde τa es la efectividad del aler´on y δa es su deflexi´on. Por lo tanto, para
calcular la distribuci´on de sustentaci´on para distintos ´angulos de deflexi´on
se debe multiplicar la distribuci´on por el producto τaδa. La efectividad del
mando se ha calculado consider´andolo como si fuese un flap simple, como se
propone en [5], adem´as de considerar que la efectividad es igual para ´angulos
de deflexi´on negativos. En la Figura 1.13 se ha representado la distribuci´on
de circulaci´on adimensional para distintos ´angulos de deflexi´on.
En programa integra esta distribuci´on y proporciona el coeficiente de susten-
taci´on que provoca un momento flector equivalente, situado en la mitad de
25](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-27-320.jpg)
![1.1. AERODIN´AMICA DEL ALA
δf (o
) 0 10 20 30 40
Intervalo CLw 0,3-1,0 0,5-1,2 0,8-1,4 1,0-1,7 1,2-2,0
CDC2
Lw
0,0431 0,0434 0,0482 0,0617 0,0808
CDCLw
0,0005 -0,0019 -0,0111 -0,0499 -0,1092
CD0 0,0067 0,0278 0,0172 0,0903 0,1674
Tabla 1.6: Coeficientes de la polar polin´omica de grado 2 en funci´on de la deflexi´on
del flap. Se se˜nala en intervalo de CL para el cual han sido calculados.
la semienvergadura, de manera que se tiene:
Clδa =
1
δa
2CL1/2
b/2qS
qSb
=
CL1/2
δa
(1.9)
Considerando una deflexi´on m´axima de 40o
, se obtiene una potencia de
mando lateral igual a 0,364 rad−1
. ´Este es un valor suficientemente grande, ya
que un valor t´ıpico de este par´ametro podr´ıa ser 0,15, como se propone en [8].
Si se desea estimar el incremento de momento de picado provocado al deflec-
tar el aler´on, se puede hacer uso de la expresi´on empleada en la deflexi´on del
flap, ecuaci´on 1.7. En la zona situada cerca del borde marginal, el coeficiente
de sustentaci´on var´ıa fuertemente (ver Figura 1.13, por lo que el incremento
de momento aerodin´amico tambi´en lo hara, resultando finalmente:
∆CMac = −0, 17∆cl (1.10)
1.1.5. C´alculo de las polares
Para el c´alculo de la aerodin´amica completa de la aeronave, es necesario
calcular la polar del ala. La polar se tomar´a como parab´olica con t´ermino
lineal en CL, de manera que el coeficiente de resistencia se expresa como:
CD = CD0 + CDCLw
· CLw + CDC2
Lw
· C2
Lw (1.11)
Los coeficientes se calcular´an mediante m´ınimos cuadrados en un intervalo
de operaci´on considerado, dejando m´argenes superiores e inferiores. En la
Tabla 1.6 se han recogido el valor de los coeficientes en funci´on del ´angulo
de deflexi´on del flap y el intervalo de CL para el cual han sido calculados.
26](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-28-320.jpg)

![1.2. EMPENAJE
δf (o
) 0 10 15
[CLmin
; CLmax ] [0; 1, 00] [0, 30; 1, 20] [0, 60; 1, 13]
CDC2
L
0,0205 0,0354 0,0969
CDCL
-0,0087 -0,0354 -0,1434
CD0 0,0077 0,0160 0,0606
Tabla 1.8: Coeficientes de la polar polin´omica de grado 2 en funci´on de la deflexi´on
del flap. Se se˜nala en intervalo de CL v´alido.
a 1/2 de la envergadura, en el caso de que el estabilizador no proporciones
sustentaci´on.
Para calcular las polares del estabilizador horizontal se supondr´a flujo
bidimensional, un Re=1E6. Los intervalos ser´an m´as amplios ya que una
vez definido el ´angulo de incidencia y el ´angulo de ataque del ala, s´olo se
tiene el grado de libertad de la deflexi´on del flap. S´olo se considerar´a hasta
una deflexi´on de 20o
, ya que a los 30o
y este reynolds el flujo se desprende
en exceso. Cabe destacar que debido a que el estabilizador puede requerir
coeficientes de sustentaci´on negativos y a que el perfil es sim´etrico, el
coeficiente lineal de la polar debe ir multiplicado por el valor absoluto del cl.
Debido a que el estabilizador horizontal se encuentra inmerso en la corriente
proveniente de la h´elice, aparecer´a un aumento de sustentaci´on debido a que
esta corriente tiene una velocidad mayor. Esto se traduce en un aumento
efectivo de la presi´on din´amica, qt, de manera que si se aplica la teor´ıa de
cantidad de movimiento empleada en el estudio del vuelo de los helic´opteros
(ver [6]):
T = 2ρSpvi(U∞ + vi) (1.13)
Sp es superficie barrida por la h´elice, vi la velocidad inducida por la misma
y U∞ la velocidad de vuelo. Por lo que la velocidad inducida resulta ser:
vi =
U2
∞ + 2T
ρSp
− U∞
2
(1.14)
Si se supone que la estela no se a contra´ıdo al alcanzar al estabilizador, este
aumento de velocidad afectar´a al 27 % de la envergadura del estabilizador,
suponiendo un di´ametro de la h´elice de 1 metro, de manera que la presi´on
din´amica sobre el estabilizador ser´a:
qt = (1 − 0, 27)q∞ + 0, 27q = (1 − 0, 27)q∞ + 0, 27
1
2
ρ(U∞ + vi)2
(1.15)
28](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-30-320.jpg)
![1.2. EMPENAJE
Introduciendo la ecuaci´on 1.14 en 1.15 y dividiendo entre q∞ se tiene:
ηt =
qt
q∞
= 0, 73 + 0, 27
1
4
(1 + 1 +
2T
ρSpU2
∞
)2
(1.16)
Finalmente, como se indica en [7], existe una p´erdida de presi´on din´amica en
la cola por estar inmersa en la estela del ala. Seg´un [3], esta perdida puede
ser considerada igual al 15 %, obteni´endose finalmete:
ηt = 0, 62 + 0, 057(1 + 1 +
2T
ρSpU2
∞
)2
(1.17)
Donde ηt se denomina eficiencia aerodin´amica de la cola y depende de la
velocidad de vuelo y de la tracci´on necesaria en cada momento. Para realizar
una primera estimaci´on de este valor se puede considerar una situaci´on de
vuelo est´andar, como por ejemplo vuelo en crucero a la altura t´ıpica de
operaci´on y con la mitad del combustible agotado:
T = D =
W
E
400 N
U∞ = 50 m/s
ρ = 0, 785 kg/m3
(1.18)
Por lo que se tiene finalmente:
ηt = 0, 86 (1.19)
Como se puede apreciar, este n´umero es pr´acticamente igual a 0,85, de
manera que el aumento de la efectividad aerodin´amica de la cola debido
a la incidencia de la corriente proveniente de la h´elice es despreciable. Sin
embargo, si se considera otra situaci´on de vuelo, por ejemplo en el despegue
(a potencia m´axima y una velocidad de 20 m/s), ηt puede alcanzar valores
cercanos a 1,20. La influencia en este par´ametro del flujo de la h´elice
depender´a de la tracci´on que se requiera y la velocidad de vuelo, de forma
que en algunas situaciones se podr´a tomar constante e igual a 0,85 y en
otros casos ser´a necesario estimarlo.
El momento aerodin´amico se tomar´a igual a CmAh = −0, 0088, resultante al
hacer la media en un intervalo de ´angulos de ataque comprendido entre los
1,3 y 7,7o
.
29](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-31-320.jpg)
![1.3. FUSELAJE, TREN DE ATERRIZAJE Y H´ELICE.
1.3. Fuselaje, tren de aterrizaje y h´elice.
Los coeficientes de resistencia de estos tres elementos se han obtenido de [5].
El coeficiente de resistencia del UAV completo se puede expresar como suma
de la contribuci´on de todos los elementos del mismo, de forma que se tiene:
CD = CDala
+ CDfus
+ CDemp + CDtren + CDSAR
+ CDEO/IR
+ CDLOS
+ CDhelice
(1.20)
De la anterior ecuaci´on ya se ha calculado el primer t´ermino, correspondiente
a la contribuci´on a la resistencia aerodin´amica del ala. El resto de t´erminos
corresponden, respectivamente, al fuselaje, empenaje, tren de aterrizaje, ra-
dar SAR, c´amara de v´ıdeo EO/IR, antena de comunicaciones LOS y la h´elice.
1.3.1. Fuselaje.
En principio se considera que el fuselaje no tiene sustentaci´on, aunque s´ı mo-
difica la pendiente de sustentaci´on del ala:
(CLα )wf = Kwf (CLα )f Kwf = 1 + 0, 025
df
b
− 0, 25
df
b
2
= 1, 0006 (1.21)
Debido al peque˜no tama˜no del fuselaje en comparaci´on con la envergadura
del ala, el factor que modifica a la pendiente de sustentaci´on del conjunto
ala-fuselaje es pr´acticamente 1.
El coeficiente de resistencia del fuselaje puede dividirse en una componente
par´asita y en otra inducida:
CDfus
= CD0fus
+ CDifus
El primer t´ermino corresponde a la resistencia par´asita del fuselaje, y puede
ser obtenido mediante la siguiente ecuaci´on emp´ırica:
CD0fus
= Rwf Cffus
(1 +
60
(lf /df )3
+ 0, 0025
lf
df
)
Swetfus
S
+ CDbfus
Donde:
Rwf es el factor de interferencia entre el ala y el fuselaje, depende
del n´umero de Mach y del n´umero de Reynolds basado en el fuselaje.
Estos valores se han tomado en la situaci´on de crucero, siendo M=0,15
y Re=6 · 106
. Utilizando la gr´afica correspondiente e interpolando, se
obtiene Rwf = 1, 10.
30](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-32-320.jpg)


![1.3. FUSELAJE, TREN DE ATERRIZAJE Y H´ELICE.
El coeficiente de resistencia de cada pata del tren depender´a de que est´e ca-
renado o no (en este caso no lo est´a), de si est´a atirantado o no y de sus
dimensiones frontales. Considerando que el neum´atico tiene un di´ametro de
10 cm, los coeficientes de resistencia de las patas delantera y trasera resultan
ser, respectivamente, igual a 0,65 y 0,62. Por lo tanto, la el coeficiente de
resistencia total del tren es igual a:
CDg = 0, 0028 (1.28)
Adem´as de aumentar la resistencia aerodin´amica, aparecer´a un momento de
cabeceo alrededor del centro aerodin´amico que es necesario estimar. Calcu-
lando el momento alrededor de este ´ultimo y admimensionalizando con la
cuerda aerodin´amica media, se tiene:
CMacg = −0, 0026 + 0, 0013αb (1.29)
1.3.3. Carga de pago exterior
En este grupo se engloba la carga de pago en la que alguna de sus partes so-
bresalen del fuselaje. S´olo se ha considerado el radar SAR, la c´amara EO/IR
y la antena de comunicaciones LOS, no considerando la antena omnidirec-
cional, la antena BLOS y las antenas del sistema AIS, ya que todos estos
elementos tienen un tama˜no muy reducido. Por simplificaci´on, se han consi-
derado el SAR y el EO/IR como dos semiesferas inmersas en una corriente
no perturbada. En [9] se recogen resultados experimentales en funci´on del
n´umero de Reynolds, considerando la situaci´on de vuelo de crucero:
ReSAR = 9, 4 · 106
−→ CD = 0, 36
ReEO/IR = 8, 2 · 106
−→ CD = 0, 38
El caso de la antena LOS es algo m´as complicado. Se asumir´a que est´a forma-
do por un cilindro con forma de elipse con relaci´on entre ejes 1:2 y un medio
elipsoide. Como se puede comprobar en trabajos como referencia [10], el coe-
ficiente de resistencia t´ıpico de este ´ultimo es de orden 10−2
, por lo que se
despreciar´a. Teniendo el en cuenta el Re de el cilindro el´ıptico en la situaci´on
de vuelo en crucero, se obtiene el siguiente coeficiente de resistencia:
ReLOS = 8, 4 · 106
−→ CD = 0, 30
Teniendo en cuenta que estos coeficientes est´an referidos a la superficie fron-
33](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-35-320.jpg)

![1.4. AERODIN´AMICA DE LA AERONAVE.
Las fuerza de sustentaci´on sobre la aeronave es:
L = Lwb + Lt cos ε − Dt sin ε
CL =
L
qS
= CLwb
+ CLh
ηh
Sh
S
cos ε − CDh
ηh
Sh
S
sin ε
(1.33)
Donde ε es el ´angulo de deflexi´on de la estela y representa la disminuci´on del
´angulo de ataque de la cola horizontal debido a la velocidad inducida de los
torbellinos desprendidos del ala; el sub´ındice h indica referente estabilizador
horizontal; ηh es la eficiencia aerodin´amica del mismo, ya definida. Si se
considera que la resistencia es despreciable frente a la sustentaci´on y que ε es
peque˜no (cos ε 0, sin ε ε, la ecuaci´on 1.33 puede simplificarse, resultado:
CL =
L
qS
= CLwb
+ CLh
ηh
Sh
S
(1.34)
Desarrollando los coeficientes de sustentaci´on del conjunto ala-fuselaje y del
estabilizador horizontal se tiene:
CLwb
= awb(αwb − αwb0)
CLh
= ah(αh + τeδe)
(1.35)
Como se vio en el estudio de los dispositivos hipersustentadores, el despliegue
de los mismos se traduce en una modificaci´on del ´angulo de ataque para
sustentaci´on nula, αwb0, siendo nula si la deflexi´on del flap tambi´en lo es.
De la misma forma se ha tratado la deflexi´on del tim´on de profundidad.
Los ´angulos de ataque del ala y del estabilizador horizontal se han tomado
desde la l´ınea de sustentaci´on nula de cada uno de ellos. El ´angulo αh puede
escribirse como:
αh = αwb − iwb + ih − ε (1.36)
Donde iwb e ih son los ´angulos de calado del conjunto ala-fuselaje y la cola
respectivamente. La deflexi´on de la estela se puede expresar como:
ε = ε0 + (
∂ε
∂α
)αwb (1.37)
En primera aproximaci´on se puede considerar ε0 nulo para un ´angulo de
deflexi´on de flaps nulo (seg´un se presenta en [5] y [3], mientras que la va-
riaci´on con el ´angulo de ataque del ala se puede modelizar como el modelo
experimental propuesto en [5]:
∂ε
∂α
= 4, 44 (KAKλKh)1,19
(1.38)
35](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-37-320.jpg)


















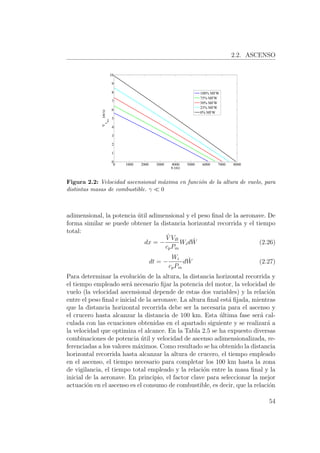













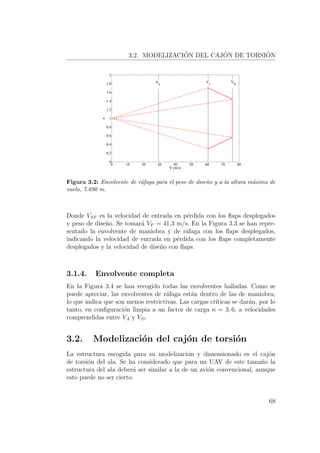

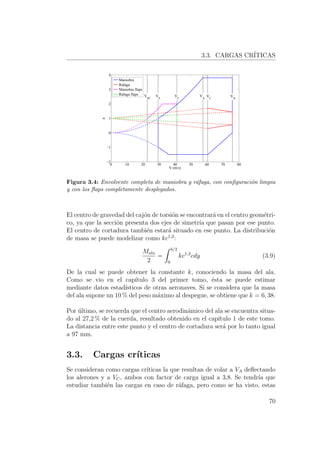




![3.4. DIMENSIONADO DE LA ESTRUCTURA.
Con las dos ecuaciones anteriores se puede obtener el espesor del revestimien-
to y de los larguerillos:
t = 0, 8 mm
ts = 0, 9 mm
Por otro lado, se tiene:
σb
σ0
3, 6E
t
b
2
= F
EN
Leq
(3.14)
De la cual se puede obtener el paso entre larguerillos:
b = 21 mm
Con este paso se puede hallar el paso entre los larguerillos, que resulta ser 21.
Este resultado no es v´alido por varios motivos. El primero es que es
imposible fabricar una pieza con un espesor tan peque˜no, ya que la l´amina
preimpregnada m´as fina tiene un espesor de 0,13 mm y, teniendo en
cuenta que el laminado debe ser sim´etrico y equilibrado, el espesor m´ınimo
debe tener 8 l´aminas, lo que dar´ıa un espesor de 1,0 mm. Por otro lado,
probablemente sea imposible fabricar unos larguerillos con un pie de tan
s´olo 6 mm, adem´as de que ser´ıa imposible instalarlos en el revestimiento, ya
que est´an separados por tan s´olo 21 mm.
Reducci´on del n´umero de larguerillos
Por las razones antes expuestas, es conveniente reducir el n´umero de largueri-
llos. Si se considera que la separaci´on m´ınima entre larguerillos es de 50 mm,
el n´umero de larguerillos ser reducir´ıa hasta 8. Para calcular el tama˜no de
los mismos y el espesor del revestimiento, se emplear´an las gr´aficas sacadas
de [11]. Conociendo b E
NL3
eq
1/4
=2,04 se obtiene:
ts
E
NLeq
1/2
= 0, 43 → ts = 0, 8 mm
h
E
NL3
eq
1/4
= 0, 95 → h = 23, 3 mm
t
E
NLeq
1/2
= 0, 95 → t = 1, 8 mm
75](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-77-320.jpg)



![Cap´ıtulo 4
Conclusiones finales
En este segundo tomo se ha profundizado en el estudio de las caracter´ısticas
de vuelo de la aeronave, calculando de manera m´as detallada su caracter´ısti-
cas aerodin´amicas y actuaciones.
Como se vio en el c´alculo del coeficiente de sustentaci´on m´aximo, el tama˜no
de los flaps definido en el tomo I se mostr´o insuficiente, por lo que hubo
que aumentarlo. Esta discrepancia entre el estudio preliminar y el detallado
se debe a que en el primero se emple´o el procedimiento propuesto en [12],
mientras que para en el segundo no se sigui´o el procedimiento propuesto en
la serie de libros, sino que se calcul´o la distribuci´on de circulaci´on a lo largo
de la envergadura del ala y se propuso un criterio para determinar el ´angulo
de ataque m´aximo.
El aumento del flap influy´o en el tama˜no y la posici´on de los alerones, ya que
se vieron disminuidos y desplazados hasta el borde marginal del ala, zona en
el que la circulaci´on en menor. Debido a esto, la potencia de control lateral
se vio disminuida, por lo que fue necesario comprobarla; compar´andola
con valores t´ıpicos de aviones civiles se comprob´o que finalmente resultaba
suficiente.
En el c´alculo de las actuaciones integrales se lleg´o a que la autonom´ıa final
resultaba ser 24 h, cumpli´endose los requerimientos exigidos y deseables.
Adem´as, se ampli´o el alcance extra en caso de incidencia, pasando de 100 a
200 km. Este sobredimensionamiento en el anteproyecto se debi´o a que se
consideraron valores conservadores del consumo espec´ıfico y de la eficiencia
aerodin´amica. El primero se tom´o inicialmente igual a 8·10−7
N/Ws, mien-
tras que una vez elegido el motor se redujo hasta 7,89 ·10−7
N/Ws. En cuanto
a la eficiencia aerodin´amica, en principio se tom´o igual a 12, pero finalmente
79](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-81-320.jpg)

![Bibliograf´ıa
[1] D.Althaus y F.X.Wortmann Stuttgarter Profilkatalog I. Institut fur Ae-
rodynamik und Gasdynamik, Universidad de Stuttgart, 1996.
[2] F. W. Diederich y M. Zlotnick. Calculated Spanwise Lift Distributions and
Aerodynamic Influence Coefficients for Unswept Wings. NACA, 1953.
[3] Egbert Torenbeek. Synthesis of Subsonic Airplane Design. Delft Univer-
sity, 1976.
[4] J. Meseguer Ruiz y A. Sanz Andr´es. Aerodin´amica b´asica. ETSIA,
[5] J. Roskam. Preliminary Calculation of Aerodynamic, Thrust and Power
Characteristics.. Roskam Aviation and Engineering Corporation Ottawa,
Kansas, 1985.
[6] A. Cuerva. Teor´ıa de los helic´opteros. ETSIA, 2009.
[7] M.A. G´omez Tierno, M. P´erez Cort´es y C. Puentes M´arquez. M´ec´anica
del vuelo. ETSIA, Madrid 2009.
[8] J. Roskham. Airplane flight dynamics and automatic flight controls, Part
I. Roskam Aviation and Engineering Corporation Ottawa, Kansas, 2003.
[9] E. N. Jacobs. Sphere Drag Test in the Variable Density Wind Tunnel.
NACA, 1929.
[10] J. A. DeMoss. Drag Measurements on an Ellipsoidal Body. Virginia
Polytechnic Institute and State University, agosto de 2007.
[11] C. Cuerno Rejado, R. Mar´ınez-Val Pe˜nalosa y E. P´erez Cobo. Enuncia-
dos de problemas. ETSIA, Madrid, 2006.
[12] Roskam J. Airplane Design, Part I: preliminary sizing of airplanes. Ros-
kam Aviation and Engineering Corporation Ottawa, Kansas, 1985.
81](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-83-320.jpg)

![Ap´endice A
Perfiles
A.1. Perfil del ala
Se consider´o un total de 10 perfiles distintos de los cuales eran conocidos
sus datos experimentales, obtenidos de [1]). Estos perfiles fueron escogidos
teniendo en cuenta dos aspectos:
Alta eficiencia aerodin´amica para el coeficiente de sustentaci´on me-
dio durante la vigilancia, que result´o ser clmedio
= 0, 49.
Alto coeficiente de sustentaci´on m´aximo, debido a que el necesario a
lo largo de toda la misi´on tambi´en lo debe ser y a que de este modo
los dispositivos hipersustentadores podr´ıan ser m´as sencillos.
Finalmente se escogi´o el perfil FX 63-143 (Figura A.1). En la Figura A.2
se ha representado la variaci´on del coeficiente de sustentaci´on en funci´on
del ´angulo de ataque. Las polares est´an representadas en la Figura A.3.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−0.05
0
0.05
0.1
0.15
Figura A.1: Forma del perfil FX 63-143.
83](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-85-320.jpg)
![A.2. PERFIL DE LOS ESTABILIZADORES VERTICAL Y
HORIZONTAL
−5 0 5 10 15 20
−0.5
0
0.5
1
1.5
2
α (º)
cl
Re = 1 ⋅ 106
Re = 1,5 ⋅ 106
Re = 2 ⋅ 106
Re = 3 ⋅ 106
Figura A.2: Variaci´on del coeficiente de sustentaci´on del perfil FX 63-143 en
funci´on del ´angulo de ataque, medido desde la cuerda, para n´umeros de Reynolds
comprendidos entre 0, 3 · 106 y 3 · 106. Datos experimentales obtenidos de [1].
−0.4 −0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0.02
cl
cd
Re=1 ⋅ 106
Re=1,5 ⋅ 106
Re=2 ⋅ 106
Re=3 ⋅ 106
Figura A.3: Polares del perfil FX 63-143 para n´umeros de Reynolds comprendidos
entre 0, 3 · 106 y 3 · 106. Datos experimentales obtenidos de [1].
A.2. Perfil de los estabilizadores vertical y
horizontal
La elecci´on del perfil de los estabilizadores vertical y horizontal es en
principio una decisi´on menos cr´ıtica que la que se ha echo del perfil del
84](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-86-320.jpg)
![A.2. PERFIL DE LOS ESTABILIZADORES VERTICAL Y
HORIZONTAL
−4 −2 0 2 4 6 8 10 12 14
−0.056
−0.054
−0.052
−0.05
−0.048
−0.046
−0.044
−0.042
−0.04
α (º)
cm
Figura A.4: Coeficiente de momento de cabeceo del perfil FX 63-137 en funci´on
del ´angulo de ataque, medido desde la cuerda, para Re = 0, 3 · 106. Datos experi-
mentales obtenidos de [1].
ala. De tres perfiles sim´etricos de los cuales se conoc´ıa sus caracter´ısticas
aerodin´amicas, se escogi´o el perfil FX 71-L-150/25 por la gran cantidad
de datos experimentales que se ten´ıa de ´el. En las siguientes figuras se
exponen las caracter´ısticas principales del perfil para distintos grados de
deflexi´on del tim´on y distintos n´umeros de Reynolds. El tim´on es de tipo
plano y la articulaci´on se encuentra a un cuarto de cuerda.
En la Figura A.5 se ha dibujado la forma del perfil. En las Figuras A.6,
A.7, A.8 y A.9 se ha representado las variaciones de cl en funci´on del
´angulo de ataque, para distintas deflexiones del tim´on y para Re = 0, 7 ·
106
, 106
, 1, 5 · 106
y 2 · 106
respectivamente. En las Figuras A.10, A.11,
A.12 y A.13 se ha representado las polar del perfil para distintos ´angulos
de deflexi´on del tim´on y para Re = 0, 7 · 106
, 106
, 1, 5 · 106
y 2 · 106
respectivamente. N´otese que para n´umeros de Re bajos (Re = 0, 7 · 106
y
106
) y deflexiones de tim´on grandes (20o
), las polar no tiene una forma
t´ıpica y similar al resto de las polares, presentando aumentos acusados
de resistencia aerodin´amica. En la Figura A.14 re ha representado la
variaci´on del coeficiente de momento de cabeceo, cm, en funci´on del ´angulo
de ataque y para distintos ´angulos de deflexi´on del tim´on, con un n´umero
de Re = 0, 7 · 106
.
85](https://image.slidesharecdn.com/0ed9503d-eb76-4561-9c96-604290c0cd3c-150513074138-lva1-app6891/85/PFC-TOMO-2-87-320.jpg)












