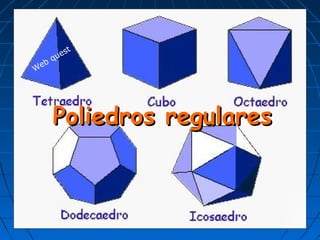
Este documento describe los poliedros regulares. Explica que los pitagóricos en el siglo VI a.C. conocían los cinco poliedros regulares y que Euclides demostró en el siglo II a.C. que no existen más. Asigna como tarea definir, clasificar y describir los poliedros regulares, incluyendo fórmulas para calcular su área y volumen, para presentar en una presentación de PowerPoint.

1. Poliedros regularesPoliedros regulares
Web quest

2. INTRODUCCIÓN
TAREA PROCESO
RECURSOS
EVALUACIÓN
CONCLUSIÓN

3. IntroducciónIntroducción
Es casi seguro que los pitagóricos en el siglo VI a.C.Es casi seguro que los pitagóricos en el siglo VI a.C.
conocían la existencia de los cinco poliedros regulares: elconocían la existencia de los cinco poliedros regulares: el
cubo, el tetraedro, el octaedro, el icosaedro y elcubo, el tetraedro, el octaedro, el icosaedro y el
dodecaedro.dodecaedro.
Euclides en el siglo II a.C. demuestra que no existe ningúnEuclides en el siglo II a.C. demuestra que no existe ningún
otro poliedro regular y proporciona métodos para suotro poliedro regular y proporciona métodos para su
construcción geométrica.construcción geométrica.
En toda época ha habido atracción por la belleza y laEn toda época ha habido atracción por la belleza y la
armonía de las regularidades de estos cuerpos, desdearmonía de las regularidades de estos cuerpos, desde
Platón que asocia los cuatro elementos que constituyen elPlatón que asocia los cuatro elementos que constituyen el
Universo con los cuatro primeros poliedros, hasta KeplerUniverso con los cuatro primeros poliedros, hasta Kepler
ya en el siglo XVI que construyó una teoría bonita peroya en el siglo XVI que construyó una teoría bonita pero
falsa sobre el sistema solar utilizando los cinco poliedrosfalsa sobre el sistema solar utilizando los cinco poliedros
regulares.regulares.
Si miramos a nuestro alrededor encontramos multitud deSi miramos a nuestro alrededor encontramos multitud de
cuerpos geométricos que son poliedros, es decir, quecuerpos geométricos que son poliedros, es decir, que
tienen sus caras formadas por polígonos, desde lo mástienen sus caras formadas por polígonos, desde lo más
pequeño a lo más grande, desde un edificio hasta una cajapequeño a lo más grande, desde un edificio hasta una caja
de zapatos o una caja de leche.de zapatos o una caja de leche.
volver

4. TareaTarea
 Definición, clasificación,Definición, clasificación,
características, denotación decaracterísticas, denotación de
fórmulas para calcular área yfórmulas para calcular área y
volumen de poliedros regulares.volumen de poliedros regulares.
 Presentación PowerPoint.Presentación PowerPoint.
volver

5. ProcesoProceso
 Definir PoliedroDefinir Poliedro
 Clasificar los distintos poliedros regulares.Clasificar los distintos poliedros regulares.
 Describir sus característicasDescribir sus características
 Denotar sus fórmulas para área yDenotar sus fórmulas para área y
volumen.volumen.
 Exponer frente a la clase el temaExponer frente a la clase el tema
investigado, a través de PowerPoint.investigado, a través de PowerPoint.
 Comentar experiencias sobre el trabajoComentar experiencias sobre el trabajo
realizado.realizado.
volver

6. RecursosRecursos
 http://www.google.com.ar/search?hl=es&biw=1152&bih=749&dhttp://www.google.com.ar/search?hl=es&biw=1152&bih=749&d
 http://es.wikipedia.org/wiki/Poliedrohttp://es.wikipedia.org/wiki/Poliedro
 http://perso.wanadoo.es/jpm/poliedros%20regulares/poliedros.hhttp://perso.wanadoo.es/jpm/poliedros%20regulares/poliedros.h
 http://www.vitutor.com/geo/esp/f_2.htmlhttp://www.vitutor.com/geo/esp/f_2.html
 http://perso.wanadoo.es/jpm/poliedros%20regulares/areayvol.hhttp://perso.wanadoo.es/jpm/poliedros%20regulares/areayvol.h
 http://mimosa.pntic.mec.es/clobo/geoweb/volum4.htmhttp://mimosa.pntic.mec.es/clobo/geoweb/volum4.htm
 http://centros5.pntic.mec.es/sierrami/dematesna/demateshttp://centros5.pntic.mec.es/sierrami/dematesna/demates
12/opciones/Mundo%20Poliedros/Poliedros12/opciones/Mundo%20Poliedros/Poliedros
%20Regulares.htm%20Regulares.htm
volver

7. EvaluaciónEvaluación
 Manejo del vocabulario específico.Manejo del vocabulario específico.
 Predisposición para trabajo grupal e individual.Predisposición para trabajo grupal e individual.
 Cumplimiento responsable de las tareasCumplimiento responsable de las tareas
asignadas en el aula en tiempo y forma.asignadas en el aula en tiempo y forma.
 Respeto por sus pares y docentes.Respeto por sus pares y docentes.
 Participación activa en clase.Participación activa en clase.
volver

8. ConclusiónConclusión
Tras la realización de este trabajo habrán comprobado que las
posibilidades de la red son enormes, hasta para estudiar
matemáticas.
Espero que este trabajo les haya servido para aprender algo más
sobre los cuerpos geométricos
volver