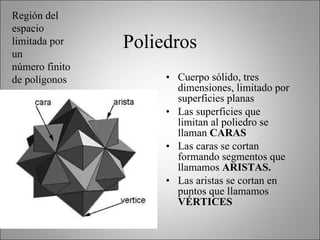
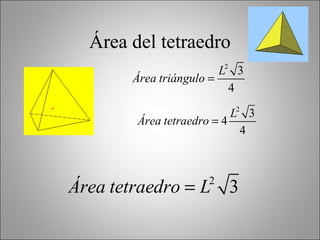
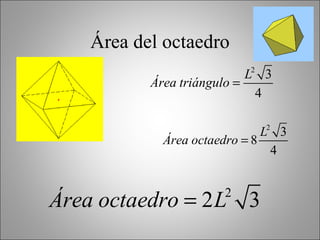
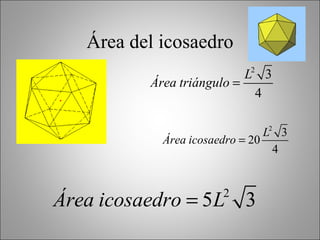
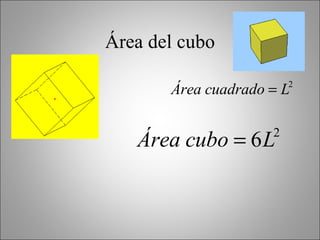
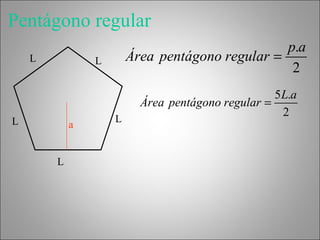
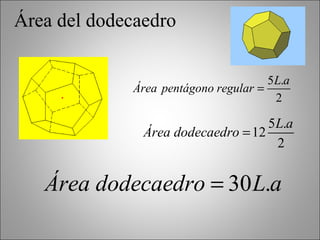
Este documento describe los poliedros geométricos, incluyendo sus características fundamentales como caras, aristas y vértices. Explica los cinco poliedros regulares definidos por caras regulares en cada vértice: el tetraedro, el octaedro, el icosaedro, el cubo y el dodecaedro. También presenta la fórmula de Euler para poliedros y calcula las áreas de los poliedros regulares. Finalmente, menciona algunos objetos de la vida real que tienen forma cilíndrica o de prisma.

1. LOS POLIEDROS GEOMETRÍA EN EL ESPACIO 3º ESO William

2. Poliedros Cuerpo sólido, tres dimensiones, limitado por superficies planas Las superficies que limitan al poliedro se llaman CARAS Las caras se cortan formando segmentos que llamamos ARISTAS. Las aristas se cortan en puntos que llamamos VÉRTICES Región del espacio limitada por un número finito de polígonos

3. Los poliedros regulares Caras polígonos regulares En cada vértice más de dos polígonos La suma de los ángulos en un vértice ha de ser menor que 360º

4. Los poliedros regulares Completa la tabla Polígonos regulares Nº de caras en un vértice Nombre del poliedro

5. Los poliedros regulares Polígonos regulares Nº de caras en un vértice Suma de los ángulos en un vértice Triángulos Triángulos Triángulos Cuadrados Pentágonos

6. Los poliedros regulares Polígonos regulares Nº de caras en un vértice Nombre Triángulos 3 Tetraedro Triángulos 4 Octaedro Triángulos 5 Icosaedro Cuadrados 3 Hexaedro o cubo Pentágonos 3 Dodecaedro

7. Los poliedros regulares Fórmula de Euler: C + V = A + 2 Caras + Vértices = Aristas + 2 Poliedros regulares Caras Vértices Aristas Tetra edro 4 4 Octa edro 8 6 Icosa edro 20 12 Hexa edro o cubo 6 8 Dodeca edro 12 20

8. Los poliedros regulares Fórmula de Euler: C + V = A + 2 Caras + Vértices = Aristas + 2 Poliedros regulares Caras Vértices Aristas Tetra edro 4 4 6 Octa edro 8 6 12 Icosa edro 20 12 30 Hexa edro o cubo 6 8 12 Dodeca edro 12 20 30

9. Los poliedros regulares http://www.walter-fendt.de/m11s/index.html http://www.mathsnet.net/geometry/solid/nets.html http://www.luventicus.org/articulos/03Tr001/index.html

10. Áreas de los poliedros regulares Área poliedro regular = Área de 1 cara x nº de caras Área del tetraedro = área del triángulo x 4 Área del octaedro = área del triángulo x 8 Área del icosaedro = área del triángulo x 20 Área del cubo = área del cuadrado x 6 Área del dodecaedro = área del pentágono x 12

11. Triángulo equilátero L L L/2 h

12. Área del tetraedro

13. Área del octaedro

14. Área del icosaedro

15. Cuadrado L L L L

16. Área del cubo

17. Pentágono regular L L L L L a

18. Área del dodecaedro

19. Balón de fútbol Le llaman “el esférico” Se obtiene cortando las puntas de un icosaedro regular, y como en cada punta hay 5 triángulos, se forman pentágonos Y como le cortamos los tres vértices a un triángulo equilátero obtenemos hexágonos regulares Es un ICOSAEDRO TRUNCADO

20. Cilindros y prismas Apisonadoras

21. Cilindros y prismas Columnas

22. Cilindros y prismas Patas de los muebles

23. Cilindros y prismas Bastones

24. Cilindros y prismas Palillos orientales

25. Cilindros y prismas Cigarrillos

26. Cilindros y prismas Espaguetis

27. Cilindros y Prismas Tubos

28. Cilindros y prismas Lápices