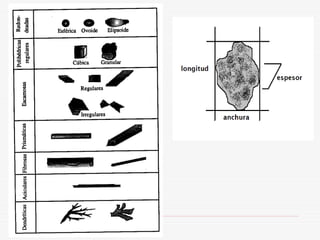
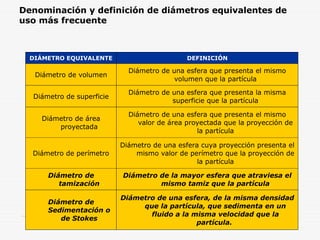
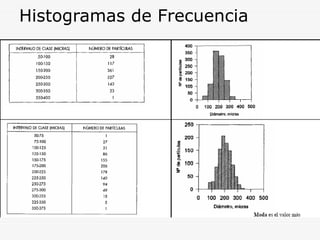
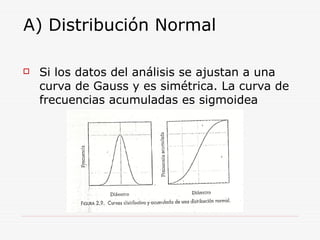
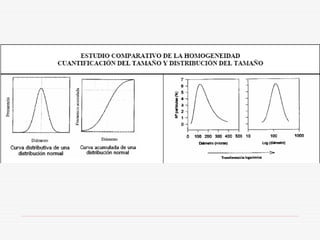
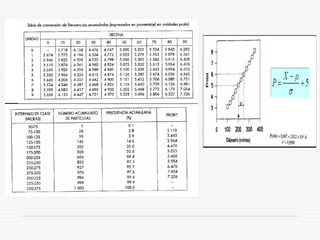
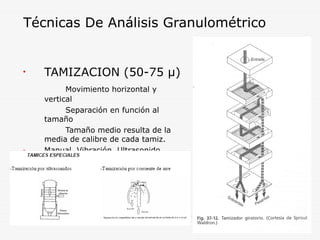
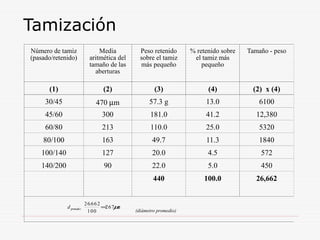
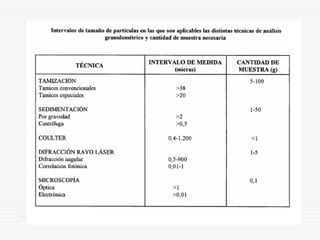
Este documento describe los métodos de análisis granulométrico para medir el tamaño y distribución de tamaños de partículas. Explica que el comportamiento de los sólidos pulverulentos depende no solo de las características del material sino también del tamaño y forma de las partículas. Luego describe métodos como la tamización, sedimentación y centrifugación para determinar la distribución de tamaños de partículas.

1. GRANULOMETRÍA
Q.F. Alfredo Bernard Claudio Delgado

2. ¿Por qué estudiar la granulometría?
 Los sólidos pulverulentos son sistemas
discontinuos, formados por partículas
individuales.
 Comportamiento no depende de las
características intrínsecas del material,
sino también de características
individuales: Forma y Tamaño
principalmente.

3. ANALISIS GRANULOMÉTRICO
 Evaluar el Tamaño.
 Aerosoles, rango limitado que permita absorción
 Lubricantes deben tener tamaños más pequeños
 Previo a una mezcla
 Determinar la DISTRIBUCIÓN de tamaños
 Superficie específica vs. tiempo de disolución
 Determinar la forma.
 Condiciona la Densidad Aparente, crítico en dosificación
sólida de comprimidos y cápsulas donde se dan procesos de
llenado volumétrico.

5. 1. MEDIDA DEL TAMAÑO DE PARTICULAS
 Sólidos en industria farmacéutica son
generalmente de forma irregular.
 Asimilar propiedades de partícula irregular
(volumen, superficie) a la de una partícula
esférica.
 Así obtenemos “esferas equivalentes” y su
diámetro, “diámetro equivalente”

6. Denominación y definición de diámetros equivalentes de
uso más frecuente
DIÁMETRO EQUIVALENTE DEFINICIÓN
Diámetro de volumen
Diámetro de una esfera que presenta el mismo
volumen que la partícula
Diámetro de superficie
Diámetro de una esfera que presenta la misma
superficie que la partícula
Diámetro de área
proyectada
Diámetro de una esfera que presenta el mismo
valor de área proyectada que la proyección de
la partícula
Diámetro de perímetro
Diámetro de una esfera cuya proyección presenta el
mismo valor de perímetro que la proyección de
la partícula
Diámetro de
tamización
Diámetro de la mayor esfera que atraviesa el
mismo tamiz que la partícula
Diámetro de
Sedimentación o
de Stokes
Diámetro de una esfera, de la misma densidad
que la partícula, que sedimenta en un
fluido a la misma velocidad que la
partícula.

7. Cubo Prisma
Volumen 106 u3 3x106 u3
Superficie 6x104 u2 1.4x105 u2
Diámetro
Equivalente
Volumen
124.08 u 89.47 u
Diámetro
Equivalente
Superficie
138.20 u (dif
11.38%)
105.55 u (dif
17.97%)
( )
2
3
.
.
6
1
d
s
d
v
π
π
=






=

8. GRANULOMETRÍA
Distribución de Tamaños
Q.F. Alfredo Bernard Claudio Delgado

9. Distribución de tamaños
 En una muestra hay muchas formas y
tamaños de partículas.
 Junto al tamaño de “partícula
promedio” se debe cuantificar la
magnitud de las diferencias de
tamaño = Distribución
 El análisis resulta una lista grande de
datos  tratamiento estadístico.

10. Histogramas de Frecuencia

12. Histograma de Frecuencias
 Aproximación más sencilla a utilizar
 Se requiere un número considerable
de datos
 Importante definir los intervalos de
clase
 La amplitud del intervalo
frecuentemente resulta de multiplicar
intervalo anterior por factor 1.4142

13.  Distribución de tamaños en NÚMERO:
Técnica de conteo de partículas
Microscopia Óptica o Electrónica
 Distribución de tamaños por PESO,
SUPERFICIE O VOLUMEN:
Técnica de Tamizado
IMPORTANTE ES VER A QUE TIPO DE
DISTRIBUCIÓN PERTENECE

14. Análisis de tamaño de
partículas

15. A) Distribución Normal
 Si los datos del análisis se ajustan a una
curva de Gauss y es simétrica. La curva de
frecuencias acumuladas es sigmoidea

17. Unidades Probits
 Es suficiente conocer la media y la desviación
estándar
 Una mejor aproximación es el transformar datos en
unidades PROBITS:

19. Técnicas De Análisis Granulométrico
• TAMIZACION (50-75 μ)
Movimiento horizontal y
vertical
Separación en función al
tamaño
Tamaño medio resulta de la
media de calibre de cada tamiz.
- Manual, Vibración, Ultrasonido
En corriente de aire.

20. Tamización
(diámetro promedio)
Número de tamiz
(pasado/retenido)
Media
aritmética del
tamaño de las
aberturas
Peso retenido
sobre el tamiz
más pequeño
% retenido sobre
el tamiz más
pequeño
Tamaño - peso
(1) (2) (3) (4) (2) x (4)
30/45 470 µm 57.3 g 13.0 6100
45/60 300 181.0 41.2 12,380
60/80 213 110.0 25.0 5320
80/100 163 49.7 11.3 1840
100/140 127 20.0 4.5 572
140/200 90 22.0 5.0 450
440 100.0 26,662
m
dpromedio µ
267
100
662
.
26
=

21. • Sedimentación
 La velocidad de sedimentación depende del
tamaño de partícula sólida (en torno a 2
micras)
 Se calcula por la ecuación de Stokes:
D= diámetro; g=gravedad; η=viscosidad de fluido;
ρ=densidad de partícula y fluido

22. Sedimentación por gravedad
 Pipeta de Andreasen.
 500 a 600 ml
 Se retiran mtras. en tiempos
establecidos
 Se secan o centrifugan  Peso
 No se extrae capa horizontal sino
una capa esférica lo que desvirtúa
ligeramente los resultados.
 Con cada toma de muestra va
disminuyendo la altura (h)
20 cm Altura
Cap. 500 ml
Toma de muestra 10 ml

24. 3) Sedimentación por Centrífuga
 Para partículas menores a 2 u
 Equipos totalmente automatizados

25. Suministra información de
tamaños en número