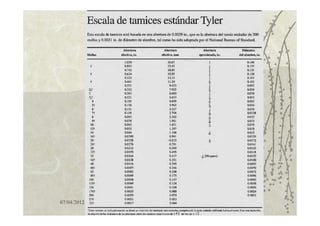
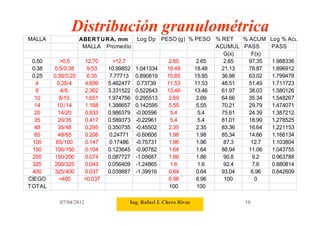
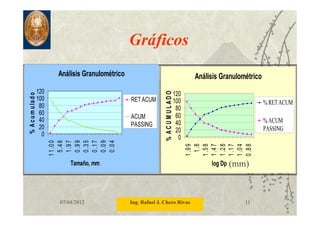
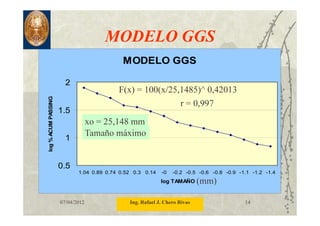
Este documento describe los procedimientos y equipos utilizados para realizar un análisis granulométrico. Explica que los tamaños de partícula se determinan mediante tamizado y asocia el tamaño con el número de aberturas por pulgada lineal de los tamices. Luego detalla diferentes tipos y tamaños de tamices y mallas, y presenta modelos matemáticos como Gates-Gaudin-Schuhmann y Rosin-Rammler para describir la distribución de tamaños.

1. UNI-FIQT
PI 146 CICLO 2012-1
ANÁLISIS Y DISTRIBUCIÓN
GRANULOMÉTRICA
Ing. RAFAEL J. CHERO RIVAS
02 abril 2012

2. 07/04/2012 Ing. Rafael J. Chero Rivas 2
GENERALIDADES
La forma usual de determinar los tamaños
de un conjunto de partículas es mediante el
análisis granulométrico utilizando una serie
de tamices. Por este procedimiento, el
tamaño de partícula se asocia al número de
aberturas que tiene el tamiz por pulgada
lineal.

3. EQUIPO PARA REALIZAR EL ANÁLISIS
GRANULOMÉTRICO
Mallas
ExistenExistenExistenExisten tamicestamicestamicestamices dededede formaformaformaforma yyyy tamatamatamatamañoooo diversosdiversosdiversosdiversos quequequeque dependendependendependendependen deldeldeldel
volumenvolumenvolumenvolumen dededede lalalala muestramuestramuestramuestra aaaa procesar,procesar,procesar,procesar, siendosiendosiendosiendo elelelel dededede ochoochoochoocho pulgadaspulgadaspulgadaspulgadas
dededede didididiámetrometrometrometro el mmmmássss utilizadoutilizadoutilizadoutilizado....
Mallas Ro-TAP

4. 07/04/2012 Ing. Rafael J. Chero Rivas 4
ABERTURAS DE MALLA
Algunas Aberturas de malla para
Series diferentes:
Malla 35: Serie TYLER
Malla 65: Serie Británica 410 (1969)
Malla 200: BS (Británica) 410 (1969)

5. MALLAS
07/04/2012 Ing. Rafael J. Chero Rivas 5

6. I
III
II
Ing. Rafael J. Chero Rivas

7. Mesh Size
(microns)
TYLER ASTM-E11 BS-410 DIN-4188
µm Mesh No. Mesh mm
5 2500 2500 0.005
10 1250 1250 0.010
15 800 800 0.015
20 625 625 0.020
22 0.022
25 500 500 0.025
28 0.028
32 0.032
36 0.036
38 400 400 400
40 0.040
45 325 325 350 0.045
50 0.050
53 270 270 300
56 0.056
63 250 230 240 0.063
71 0.071
75 200 200 200
80 0.080
90 170 170 170 0.090
100 0.100
106 150 140 150
112 0.112
125 115 120 120 0.125
140 0.140
150 100 100 100
160 0.160
180 80 80 85 0.180
200 0.200
212 65 70 72
Diferentesseriesdetamicesyequivalencias
Ing. Rafael J. Chero Rivas

8. 07/04/2012 Ing. Rafael J. Chero Rivas 8

9. 07/04/2012 Ing. Rafael J. Chero Rivas 9

10. 07/04/2012 Ing. Rafael J. Chero Rivas 10
MALLA ABERT URA, mm Log Dp PESO (g) % PESO % RET % ACUM Log % Acum
MALLA Promedio ACUMUL PASS PASS
G(x) F(x)
0.50 >0.5 12.70 >12.7 2.65 2.65 2.65 97.35 1.988336
0.38 0.5/0.38 9.53 10.99852 1.041334 18.48 18.48 21.13 78.87 1.896912
0.25 0.38/0.25 6.35 7.77713 0.890819 15.85 15.85 36.98 63.02 1.799478
4 0.25/4 4.699 5.462477 0.73739 11.53 11.53 48.51 51.49 1.711723
8 4/8. 2.362 3.331522 0.522643 13.46 13.46 61.97 38.03 1.580126
10 8/10. 1.651 1.974756 0.295513 2.69 2.69 64.66 35.34 1.548267
14 10./14 1.168 1.388657 0.142595 5.55 5.55 70.21 29.79 1.474071
20 14/20 0.833 0.986379 -0.00596 5.4 5.4 75.61 24.39 1.387212
35 20/35 0.417 0.589373 -0.22961 5.4 5.4 81.01 18.99 1.278525
48 35/48 0.295 0.350735 -0.45502 2.35 2.35 83.36 16.64 1.221153
65 48/65 0.208 0.24771 -0.60606 1.98 1.98 85.34 14.66 1.166134
100 65/100 0.147 0.17486 -0.75731 1.96 1.96 87.3 12.7 1.103804
150 100/150 0.104 0.123645 -0.90782 1.64 1.64 88.94 11.06 1.043755
200 150/200 0.074 0.087727 -1.05687 1.86 1.86 90.8 9.2 0.963788
325 200/325 0.043 0.056409 -1.24865 1.6 1.6 92.4 7.6 0.880814
400 325/400 0.037 0.039887 -1.39916 0.64 0.64 93.04 6.96 0.842609
CIEGO <400 <0.037 6.96 6.96 100 0
TOTAL 100 100
Distribución granulométrica

11. 07/04/2012 Ing. Rafael J. Chero Rivas 11
Gráficos
Análisis Granulométrico
0
20
40
60
80
100
120
11.00
5.46
1.97
0.99
0.35
0.17
0.09
0.04
Tamaño, mm
%Acumulado
RET ACUM
ACUM
PASSING
Análisis Granulométrico
0
20
40
60
80
100
120
1.99
1.8
1.58
1.47
1.28
1.17
1.04
0.88
log Dp
%ACUMULADO
% RETACUM
% ACUM
PASSING
(mm)

12. 07/04/2012 Ing. Rafael J. Chero Rivas 12
Se han presentado una serie de modelos
para describir la distribución de tamaños en
un análisis granulométrico. Todos son
relaciones empíricas, las cuales en mayor o
menor grado intentan describir la
distribución por tamaños en las Operaciones
de reducción de tamaño.
A continuación se presentan dos modelos
que son de gran utilidad.
Funciones de Distribución por tamaños

13. 07/04/2012 Ing. Rafael J. Chero Rivas 13
1. Función de Distribución de Gates-Gaudin-
Schuhmann (GGS)
F(x) = 100(x/xo)n
donde xo: Tamaño máximo de partícula en esa
distribución
Tomando logaritmos:
Log F(x) = log (100/xo
n) + n log x
donde: F(x): % acumulado passing.
A mayor n, mas uniforme es el producto.

14. 07/04/2012 Ing. Rafael J. Chero Rivas 14
MODELO GGS
MODELO GGS
0.5
1
1.5
2
1.04 0.89 0.74 0.52 0.3 0.14 -0 -0.2 -0.5 -0.6 -0.8 -0.9 -1.1 -1.2 -1.4
log TAMAÑO
log%ACUMPASSING
F(x) = 100(x/25,1485)^ 0,42013
r = 0,997
(mm)
xo = 25,148 mm
Tamaño máximo

15. 07/04/2012 Ing. Rafael J. Chero Rivas 15
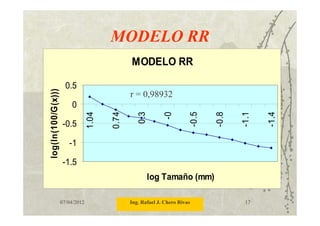
2. Función de Distribución Rosin-
Rammler (RR)
F(x) = 100(1 – exp [-(x/xr)a])
a, xr: constantes
F(x) = 100 – 100 exp[-(x/xr)a]
100 exp[-(x/xr)a] = 100 – F(x) = G(x)
G(x): Peso retenido acumulado

16. 07/04/2012 Ing. Rafael J. Chero Rivas 16
100/G(x) = exp(x/xr)a
ln (100/G(x)) = (x/xr)a
log (ln (100/G(x))) = a log x – a log xr

17. 07/04/2012 Ing. Rafael J. Chero Rivas 17
MODELO RR
MODELO RR
-1.5
-1
-0.5
0
0.5 1.04
0.74
0.3
-0
-0.5
-0.8
-1.1
-1.4
log Tamaño (mm)
log(ln(100/G(x)))
r = 0,98932

18. 07/04/2012 Ing. Rafael J. Chero Rivas 18

19. 07/04/2012 Ing. Rafael J. Chero Rivas 19
Definición d80
d80: Es el tamaño de la abertura del tamiz
por donde pasa el 80% del sólido que se
está tamizando.

20. Ejemplo
El análisis granulométrico de la descarga de
un molino es el siguiente:
MALLA % Peso
35 16,13
48 30,04
65 9,53
80 3,40
100 8,50
200 9,50
- 200 22,9
Encontrar el d8 0 del
producto del molino y
determinar a que modelo
se ajusta mejor el
análisis granulométrico.