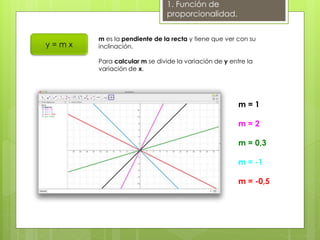
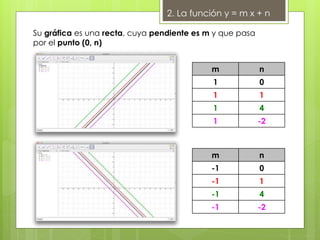
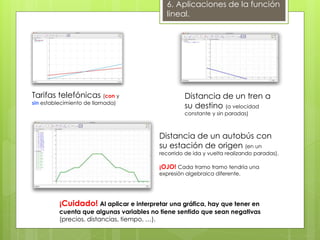
El documento detalla las funciones lineales, incluyendo la definición de la pendiente y la forma general de ecuaciones de rectas. También se abordan aplicaciones prácticas de estas funciones, como tarifas telefónicas y trayectos de vehículos, y se ofrece un análisis conjunto para determinar la opción más beneficiosa según el uso. Finalmente, se menciona que la presentación se basa en un libro de matemáticas y es parte de un trabajo de fin de máster.

1. Tema 11
Funciones Lineales
Luis Pérez Manzano

2. 1. Función de
proporcionalidad.
y = m x
m es la pendiente de la recta y tiene que ver con su
inclinación.
Para calcular m se divide la variación de y entre la
variación de x.
m = 1
m = 2
m = 0,3
m = -1
m = -0,5

3. 2. La función y = m x + n
Su gráfica es una recta, cuya pendiente es m y que pasa
por el punto (0, n)
m n
1 0
1 1
1 4
1 -2
m n
-1 0
-1 1
-1 4
-1 -2

4. 3. Recta de la que se conoce un
punto y la pendiente.
Datos
conocidos
Ecuación
de la recta
• La recta tiene pendiente m.
• La recta pasa por el punto (x0, y0).
y = y0 + m (x – x0)
Ecuación punto – pendiente

5. 4. Ecuación de la recta que
pasa por dos puntos.
Datos
conocidos
Cálculo de
la ecuación
• La recta pasa por el punto (x1, y1).
• La recta pasa por el punto (x2, y2).
1. Cálculo de la pendiente de la recta:
m = (y2 – y1) / (x2 – x1)
2. Usar la ecuación punto – pendiente con m y con
cualquiera de los dos puntos de los datos conocidos.

6. 5. Forma general de la
ecuación de una recta.
- Si a = 0 y b ≠ 0 , entonces se tiene una recta horizontal
paralela al eje OX.
- Si a ≠ 0 y b = 0, entonces no corresponde a una
función, ya que sería x = c/a, con lo que habría infinitos
puntos cuya primera coordenada coincidiría.
- Si b ≠ 0, entonces siempre la recta corresponde con la
gráfica de una función.
- Si a = 0 y b = 0, entonces tiene que ser c = 0 y no
representa a una gráfica.
Ecuación general
de la recta
a x + b y = c
Observaciones

7. 6. Aplicaciones de la función
lineal.
Tarifas telefónicas (con y
sin establecimiento de llamada)
Distancia de un tren a
su destino (a velocidad
constante y sin paradas)
Distancia de un autobús con
su estación de origen (en un
recorrido de ida y vuelta realizando paradas).
¡OJO! Cada tramo tramo tendría una
expresión algebraica diferente.
¡Cuidado! Al aplicar e interpretar una gráfica, hay que tener en
cuenta que algunas variables no tiene sentido que sean negativas
(precios, distancias, tiempo, …).

8. 7. Estudio conjunto de dos
funciones.
Tarifas telefónicas (con y
sin establecimiento de llamada)
Se representan juntas para
ver cuál nos interesa más
según el uso que vayamos
a hacer.
• Se calcula el punto de corte de las rectas.
• Si vamos a hablar menos de 5 minutos (la x del punto de
corte), entonces nos conviene la tarifa sin establecimiento de
llamada.
• Si vamos a hablar más de 5 minutos (la x del punto de corte),
entonces nos conviene la tarifa con establecimiento de
llamada.

9. Presentación.
• La presentación está realizada en base al contenido
del libro:
Colera, J., García, R., Gaztelu, I. y Oliveira, M. J. (2006).
Educación Secundaria: Matemáticas 3. Madrid: Grupo
Anaya, S. A.
• Todas las imágenes incluidas son de elaboración
propia.
• Esta diapositiva forma parte de un Trabajo Fin de
Máster.