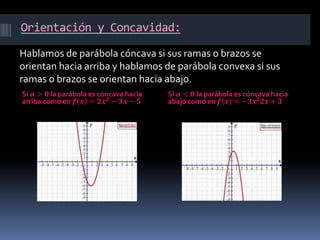
La función lineal se representa como f(x)=mx+b, donde m es la pendiente y b es el punto de corte con el eje y. La función cuadrática se representa como y=ax2+bx+c, donde a determina si la parábola es cóncava hacia arriba o abajo. La función cuadrática tiene características como raíces, eje de simetría y vértice.

1. FUNCIÓN LINEAL Y FUNCIÓN
CUADRÁTICA
Definiciones y representaciones gráficas

2. Definición:
Función Lineal
En geometría y el álgebra elemental, una función lineal es
una función polinómica de primer grado; es decir, una
función cuya representación en el plano cartesiano es una
línea recta. Esta función se puede escribir como:
f(x) = mx + b
Donde m y b son constantes reales y x es una variable real.
La constante m es la pendiente de la recta, y b es el punto
de corte de la recta con el eje y. Si se modifica m entonces
se modifica la inclinación de la recta, y si se modifica b,
entonces la línea se desplazará hacia arriba o hacia abajo.

3. Pendiente
Representación Gráfica
m es la pendiente de la recta.
Ordenada al origen:
La ordenada al origen "b" es el valor donde la recta corta al
eje “y”.

4. Características de la pendiente:
La pendiente es la inclinación de la recta con respecto al
eje de abscisas.
• Si m > 0 la función es creciente y el ángulo que
forma la recta con la parte positiva del eje OX es agudo.
• Si m < 0 la función es decreciente y el ángulo que
forma la recta con la parte positiva del eje OX es obtuso.
• Si m = 0 la función es contante.

5. Definición:
Función Cuadrática:
Una función cuadrática de una variable es una función polinómica definida por:
y=𝑎𝑥2
+ 𝑏𝑥 + 𝑐 con a≠0
Representación Analítica:
Hay tres formas de escribir una función cuadrática,
aplicables según el uso que se le quiera dar a la función.

6. Forma Polinómica:
La forma polinómica de una función cuadrática
corresponde a la del polinomio de segundo grado, escrito
convencionalmente como:
𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 con 𝑎 ≠ 0
Forma factorizda:
La forma polinómica de una función cuadrática
corresponde a la del polinomio de segundo grado, escrito
convencionalmente como:
𝑓 𝑥 = 𝑎(𝑥 − 𝑥1)(𝑥 − 𝑥2)
siendo 𝑎 el coeficiente principal de la función, y 𝑥1; 𝑥2 las
raíces de f(x).

7. Forma canónica:
Toda función cuadrática puede ser expresada mediante el
cuadrado de un binomio de la siguiente manera:
𝑓 𝑥 = 𝑎(𝑥 − ℎ)2 + 𝑘
siendo a el coeficiente principal y el par ordenado (h,k)las
coordenadas del vértice de la parábola.

8. Diremos que una parábola es la representación gráfica de
una función cuadrática.
Dicha parábola tendrá algunas características o elementos
bien definidos dependiendo de los valores de la ecuación que
la generan.
Estas características o elementos son:
Representación Gráfica
Ordenada al origen:
En el eje de ordenadas (Y) la primera coordenada es cero,
por lo que el punto de corte en el eje de las ordenadas lo
marca el valor de c (0, c).

9. Orientación y Concavidad:
Si 𝒂 > 𝟎 la parábola es cóncava hacia
arriba como en 𝒇 𝒙 = 𝟐𝒙 𝟐
− 𝟑𝒙 − 𝟓
Si 𝒂 < 𝟎 la parábola es cóncava hacia
abajo como en 𝒇 𝒙 = −𝟑𝒙 𝟐
𝟐𝒙 + 𝟑
Hablamos de parábola cóncava si sus ramas o brazos se
orientan hacia arriba y hablamos de parábola convexa si sus
ramas o brazos se orientan hacia abajo.

10. Raíces:
Las raíces (o ceros) de una función cuadrática, como en
toda función, son los valores de 𝑥, para los cuales 𝑦 =
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0. Son denotadas habitualmente como:
𝑥1; 𝑥2 dependiendo del valor del discriminante Δ
definido como ∆ = 𝑏2 − 4𝑎𝑐

11. Eje de simetría:
El eje de simetría de una parábola es una recta vertical que
divide simétricamente a la curva; es decir, intuitivamente la
separa en dos partes congruentes. Su ecuación está dada
por:
𝑥 =
𝑥1+𝑥2
2
Vértice:
El vértice de la parábola es el punto de corte (o punto de
intersección) del eje de simetría con la parábola.