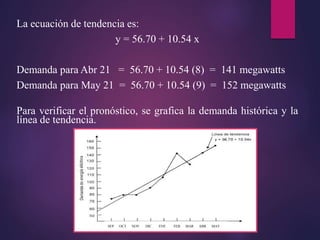
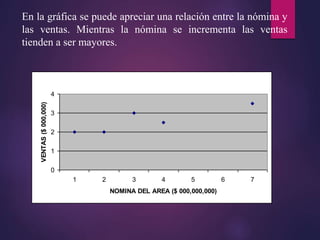
Este documento presenta diferentes métodos para realizar pronósticos de demanda. Brevemente describe métodos cualitativos basados en la experiencia y métodos cuantitativos basados en modelos matemáticos y datos históricos, incluyendo promedios móviles, suavización exponencial y proyección de tendencias. El objetivo es predecir eventos futuros como demanda de productos mediante el análisis de datos pasados y la aplicación de estas técnicas estadísticas.

1. PRONOSTICO
DEMANDA
M.B.A. Julio La Cruz

2.  Es el arte y la ciencia de predecir eventos futuras.
 Se apoya en algún modelo matemático.
 Valora la experiencia y buen juicio del administrador.
 No existe un modelo único de solución. Lo que mejor
funciona en una circunstancia, puede no adaptarse a otra.
PRONOSTICO

3. a) METODOS CUALITATIVO
Eexperiencia del tomador de decisiones.
Conoce desempeño de la variable en cuestión, ante
cualquier escenario..
Utiliza:
METODOS:
Opinión de administradores.
Opinión de la fuerza de ventas.
Encuesta a clientes.
.

4. b) METODOS CUANTITATIVOS.-
Modelos matemáticos basados en datos históricos.
Pueden ser:
Modelo de Series de Tiempo.- Emplea los valores de la
variable a pronosticar.
Modelo Causal.- Determina la tendencia del pronóstico
en base a otras variables accesibles.

5. • Empleando datos históricos de la misma variable.
• Tipos:
Promedio móvil
Suavización exponencial
Proyección de tendencia.
MODELOS DE SERIES DE TIEMPO

6.  La demanda del siguiente periodo se asume igual al
promedio aritmético simple de las demandas de los últimos
“n” meses.
PROMEDIO =  demandas en “n” periodos previos
MOVIL n
 Cada mes que pasa el dato del mes más reciente se
actualiza y el primer mes se suprime.
1. PROMEDIO MOVIL

7. VENTAS PROMEDIO MOVIL
Enero 10
Febrero 12
Marzo 13
Abril 16 ( 10+12+13 ) / 3 = 11
Mayo 19 ( 12+13+16 ) / 3 = 13
Junio 23 ( 13+16+19 ) / 3 = 16
Julio 26 ( 16+19+23 ) / 3 = 19
Agosto 30 ( 19+23+26 ) / 3 = 22
Septiembre 28 ( 23+26+30 ) / 3 = 26
Octubre 18 ( 26+30+28 ) / 3 = 28
Noviembre 16 ( 30+28+18 ) / 3 = 25
Diciembre 14 ( 28+18+16 ) / 3 = 20
EJEMPLO
Calcular el promedio móvil de tres meses, a partir de abril.

8. VENTAS PROMEDIO MOVIL
Reales
Enero 36
Febrero 42
Marzo 40
Abril 38 ( + ) / =
Mayo 36 ( + ) / =
Junio 33 ( + ) / =
Julio 30 ( + ) / =
Agosto 26 ( + ) / =
Septiembre 25 ( + ) / =
Octubre 24 ( + ) / =
Noviembre 28 ( + ) / =
Diciembre 30 ( + ) / =
Ejm 1b
Calcular el promedio móvil, de dos meses, a partir de abril.

9.  En el Promedio Móvil se ponderan las demandas de los
“n” periodos previos.
 Los pesos se determinan sobre el conocimiento de la
estacionalidad del negocio.
 Se dará mayor peso a los datos de los meses cuyo
comportamiento sea más similar al mes a pronosticar.
2. PROMEDIO MOVIL PONDERADO

10. PESOS PERIODOS
3 Ultimo mes
2 Dos meses antes
1 Tres meses antes
6 Suma de los pesos.
EJEMPLO
La empresa debe pronosticar las ventas de su producto, a
partir de abril. Empleará promedio móvil ponderado, de tres
meses, con ponderación: 3, 2, 1

11. Los resultados del pronóstico son:
VENTAS PROMEDIO MOVIL
PONDERADO
Enero 10
Febrero 12
Marzo 13
Abril 16 ( 10+12*2+13*3 ) / 6 = 12
Mayo 19 ( 12+13*2+16*3 ) / 6 = 14
Junio 23 ( 13+16*2+19*3 ) / 6 = 17
Julio 26 ( 16+19*2+23*3 ) / 6 = 20
Agosto 30 ( 19+23*2+26*3 ) / 6 = 23
Septiembre 28 ( 23+26*2+30*3 ) / 6 = 27
Octubre 18 ( 26+30*2+28*3 ) / 6 = 28
Noviembre 16 ( 30+28*2+18*3 ) / 6 = 23
Diciembre 14 ( 28+18*2+16*3 ) / 6 = 18

12. VENTAS PROMEDIO MOVIL
PONDERADO
Enero 26
Febrero 32
Marzo 30
Abril 28 ( 5*30+3*32+1*26) / 9 = 30.2
Mayo 26 ( 5*28+3*30+1*32) / 9 = 29.1
Junio 23 ( + + ) / =
Julio 20 ( + + ) / =
Agosto 16 ( + + ) / =
Septiembre 15 ( + + ) / =
Octubre 14 ( + + ) / =
Noviembre 18 ( + + ) / =
Diciembre 20 ( + + ) / =
Ejem 2b.
Calcular el promedio móvil ponderado de tres meses (5,3,1). A
partir de Abril.

13. La estimación de la demanda del periodo (Ft) es igual a la
estimación que se hizo para el periodo previo (Ft-1) más una
fracción (α) de la diferencia entre la demanda real del
periodo previo (At-1) y su correspondiente estimado:
Ft=Ft-1 + α (At-1 – Ft-1)
La constante de suavización α tiene un valor entre 0 y 1.
Se suele asignar un valor alto cuando se requiere dar mayor
peso a los datos recientes.
3. SUAVIZACIÓN EXPONENCIAL

14. Trim. Tn Pronostico Pronóstico
(real) α = 0.10 α = 0.50
1 180 175 175
2 168 176 = 175 + 0.10 ( 180-175 ) 178
3 159 175 = 176 + 0.10 ( 168-176 ) 173
4 175 173 = 175 + 0.10 ( 159-175 ) 166
5 190 173 = 173 + 0.10 ( 175-173 ) 170
6 205 175 = 173 + 0.10 ( 190-173 ) 180
7 180 178 = 175 + 0.10 ( 205-175 ) 193
8 182 178 = 178 + 0.10 ( 180-178 ) 186
9 179 = 178 + 0.10 ( 182-178 ) 184
EJEMPLO
En un puerto se ha descargado grandes cantidades de carne de
barcos sudamericanos. El administrador de operaciones del puerto
necesita pronosticar y se le pide utilice el método de Suavización
Exponencial. Debe considerar valores de α de 0.10 y 0.50.

15. Tn Pronost. Desv. Pronost. Desv.
(Real) α = 0.10 Abs. α=0.50 Abs.
α=0.10 α=0.50
1 180 175 5 175 5
2 168 176 8 178 10
3 159 175 16 173 14
4 175 173 2 166 9
5 190 173 17 170 20
6 205 175 30 180 25
7 180 178 2 193 13
8 182 178 4 186 4
84 100
MAD = Σ I desviaciones I 84/8 = 10.50 100/8 = 12.5
n
Calculo de MAD para cada valor de α
Se prefiere una cte. de suavización “” = 0.10 ( MAD menor )

16. Trim. Tn Pronostico Pronóstico
(real) α = 0.25 α = 0.60
1 200 180 180
2 188 = 180 + 0.25 ( 200 -180)
3 179
4 195
5 210
6 225
7 200
8 202
Ejem 3b:
En un puerto se ha descargado grandes cantidades de carne de
barcos sudamericanos. El administrador de operaciones del puerto
necesita pronosticar y se le pide utilice el método de Suavización
Exponencial. Se asumen valores de α de 0.25 y 0.60.

17. Trim. Tn Pronostico Pronóstico
(real) α = 0.35 α = 0.70
1 330 350 350
2 275 = +0.35( - )
3 250 = +0.35( - )
4 200 = +0.35( - )
5 220
6 240
7 260
8 300
Ejem 3c:
En un puerto se ha descargado grandes cantidades de carne de
barcos sudamericanos. El administrador de operaciones del puerto
necesita pronosticar y se le pide utilice el método de Suavización
Exponencial. Se asumen valores de α de 0.35 y 0.70.

18. Ajusta una línea de tendencia de una serie de puntos de datos
históricos y la proyecta al futuro.
Utilizando el método de mínimos cuadrados, la ecuacion de
la recta es:
Donde:
b = Σ xy – n x y
Σ x2 – n x 2
a = y – bx
En caso existan variaciones recurrentes en ciertas estaciones
del año, será necesario realizar un ajuste en la línea de
tendencia.
4. PROYECCIÓN DE TENDENCIA
Y = a + bx

19. EJEMPLO
La demanda de energía eléctrica en megawatts para los meses de
septiembre a marzo 2021, como se muestra . Ajustar una línea de
tendencia a estos datos y pronosticar la demanda de abril y mayo
del 2021.
Mes Demanda Mes Demanda
Energía Energía
Sep 20 74 Ene 21 105
Oct 20 79 Feb 21 142
Nov 20 80 Mar 21 122
Dic 20 90

20. Para aplicar mínimos cuadrados:
Mes Periodo Demanda x2 XY
X Energía Y
Sep 20 1 74 1 74
Oct 20 2 79 4 158
Nov 20 3 80 9 240
Dic 20 4 90 16 360
Ene 21 5 105 25 525
Feb 21 6 142 36 852
Mar 21 7 122 49 854
Σx = 28 Σy = 692 Σx2 = 140 Σxy = 3063

21. x = Σx = 28 = 4 y = Σy = 692 = 98.86
n 7 n 7
b = Σx y – n x y = 3,063 – 7 (4) (98.86) = 10.54
Σx 2 – n x 2 140 - (7) (4)2
a = y – bx = 98.86 – 10.54 (4) = 56.70

22. La ecuación de tendencia es:
y = 56.70 + 10.54 x
Demanda para Abr 21 = 56.70 + 10.54 (8) = 141 megawatts
Demanda para May 21 = 56.70 + 10.54 (9) = 152 megawatts
Para verificar el pronóstico, se grafica la demanda histórica y la
línea de tendencia.
2000 2001 2002 2003 2004 2005 2006 2007 2008
SEP OCT NOV DIC ENE FEB MAR ABR MAY

23. EJEM 4b
La demanda de GASEOSAS en cajas para los meses de
septiembre a marzo 2021, como se muestra . Ajustar una línea de
tendencia a estos datos y pronosticar la demanda de abril y mayo
del 2021.
Mes Demanda Mes Demanda
(Cajas) (Cajas)
Sep 20 220 Ene 21 500
Oct 20 250 Feb 21 550
Nov 20 300 Mar 21 480
Dic 20 400

24. El PRONÓSTICO se realiza empleando una variable distinta a la
variable del pronóstico, con una correlación suficiente.
La mejor correlación se da cuando “r” el coeficiente de
correlación toma valores más cercanos a 1 (0 < r < 1).
r = n Σ xy - Σ xΣy .
[n Σx2 – (Σx)2] * [n Σy2 – (Σy)2]
Variables causales: tasa de desempleo, índices de precios, precio
de venta, presupuesto de publicidad, etc.
MODELO CAUSAL

25. EJEMPLO
Una inmobiliaria se ha percatado que sus ventas dependen del ingreso del
total de los asalariados de la zona (nómina salarial). El cuadro adjunto
muestra sus ventas y la nómina salarial local de los años 2015 al 2020.
SE PIDE:
a) Estime cuanto serían sus ventas si nomina local fuese 600 millones.
b) Calcule la correlación entre ambas variables, para validar pronóstico
VENTAS (Y) NOMINA SALARIAL (X)
($ 000,000) ($ 000,000,000)
2.0 1
3.0 3
2.5 4
2.0 2
2.0 1
3.5 7

26. En la gráfica se puede apreciar una relación entre la nómina y
las ventas. Mientras la nómina se incrementa las ventas
tienden a ser mayores.
0
1
2
3
4
1 2 3 4 5 6 7
NOMINA DEL AREA ($ 000,000,000)
VENTAS
($
000,000)

27. VENTAS (Y) NOMINA (X) X2 XY
2.0 1 1 2.0
3.0 3 9 9.0
2.5 4 16 10.0
2.0 2 4 4.0
2.0 1 1 2.0
3.5 7 49 24.5
Σy=15.0 Σx=18 Σx2=80 Σxy=51.5

28. x = Σx = 18 = 3 ; y = Σy = 15 = 2.5
6 6 6 6
b = Σxy – n x y = 51.5 – (6)(3)(2.5) = 0.25
Σx2 – n x 2 80 – 6 (32)
a = y – bx = 2.5 – 0.25 (3) = 1.75
La ecuación es: y = 1.75 + 0.25 x
ó VENTAS = 1.75 + 0.25 NOMINA

29. Si el estimado de la nómina salarial fuese $600 millones, las
ventas pronosticadas serían:
VENTAS (en cientos de miles) = 1.75 + 0.25 (6)
VENTAS = $ 325,000

30. b) Calculo del coeficiente de correlación.
En el ejemplo anterior se requiere validar el pronóstico,
determinando la correlación entre las variables referidas
y x x2 xy y2
2.0 1 1 2.0 4.0
3.0 3 9 9.0 9.0
2.5 4 16 10.0 6.25
2.0 2 4 4.0 4.0
2.0 1 1 2.0 4.0
3.5 7 49 24.5 12.3
Σy=15.0 Σx=18 Σx2=80 Σxy=51.5 Σy2=39.5

31. r = nΣxy – Σx Σy
[nΣx2 – (Σx)2] [nΣy2 – (Σy)2]
r = 6(51.5) – 18 (15.0)
[6(80) - 182] [6(39.5) - 152]
r = 0.901
El valor de r muestra una correlación significativa y ayuda a
confirmar la estrecha relación entre las dos variable.s

32. EJERCICIO D
Una constructora de oficinas se ha percatado que sus ventas dependen de la
nómina salarial en el área. El cuadro adjunto muestra ventas y la nómina
salarial de los trabajadores asalariados de la zona (2015-2020)
SE PIDE:
a) Estime cuanto serían sus ventas si nomina local fuese 700 millones.
b) Calcule la correlación entre ambas variables, para validar pronóstico
VENTAS (Y) NOMINA LOCAL (X)
($ 000,000) ($ 000,000,000)
3.0 4
4.0 3
3.5 4
2.8 2
3.7 3
4.2 5

33.  Para determinar la efectividad del pronóstico y tomar las
medidas de ajuste se calcula la señal de rastreo
 Cuando la señal de rastreo cae fuera de los límites, existe un
problema con el método.
 Se calcula como la suma de los errores corrientes (RSFE)
dividido entre la desviación media absoluta (MAD)
Señal de Rastreo = RSFE = Σ (errores de pronóstico)
MAD Σ | errores de pronóstico |
n
MONITOREO Y CONTROL

34. EJEMPLO
Se tiene ventas reales y pronosticadas. Calcular la señal de rastreo
(SR) y evaluar el pronóstico.
Venta Venta Error RSFE Error Error MAD SR
Pron. Real Pron. Acum.
1 100 90 -10 -10 10 10 10 -1
2 100 95 - 5 -15 5 15 7.5 -2
3 100 115 +15 0 15 30 10 0
4 110 100 -10 -10 10 40 10 -1
5 110 125 +15 + 5 15 55 11 +0.5
6 110 140 +30 +35 30 85 14.2 +2.5
SR = RSFE = 35 = 2. 5
MAD 14.2
La SR se encuentra entre límites aceptables –2 y +2 . 5

35. TIPOS DE CORRELACIÓN
r = +1
Positiva
Perfecta
0 < r < 1
Positiva
r = 0
Sin
correlación
r = -1
Negativa
Perfecta

36. 1º Determinar el OBJETIVO del pronóstico.
2º Seleccionar las VARIABLES a pronosticar.
3º Determinar el HORIZONTE de tiempo
4º Seleccionar el MODELO a utilizar.
5º Levantar datos.
6º Validar el modelo.
7º Hacer el pronóstico
8º Documentar los resultados.
ETAPAS