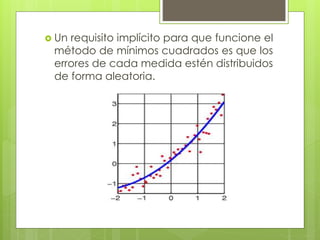
El documento presenta el método de mínimos cuadrados y su aplicación para analizar series de tiempo. El método intenta encontrar la función que mejor se ajusta a un conjunto de datos minimizando la suma de los cuadrados de los residuos. Se describe cómo se puede usar para identificar la tendencia secular de una serie y predecir valores futuros mediante la ecuación de la recta de tendencia. Como ejemplo, se muestra cómo predecir las ventas futuras de una zapatería en 2015 usando sus ventas históricas.

1. INTEGRANTES
Sayri Pérez Bañales
Arturo Sánchez Padilla
Eduardo Gracián Ayala
Karla Cárdenas Gálvez
MÉTODO DE
MINIMOS
CUADRADOS
EQUIPO #2

2. Mínimos cuadrados
 Es una técnica de optimización
matemática que, dada una serie de
mediciones, intenta encontrar una
función que se aproxime a los datos (un
"mejor ajuste"). Intenta minimizar la suma
de cuadrados de las diferencias
ordenadas (llamadas residuos) entre los
puntos generados por la función y los
correspondientes en los datos.

3.  Mínimos cuadrados es una técnica
de análisis numérico enmarcada
dentro de la optimización
matemática, en la que, dados un
conjunto de pares ordenados:
variable independiente, variable
dependiente, y una familia de
funciones, se intenta encontrar
la función continua, dentro de dicha
familia, que mejor se aproxime a los
datos.

4.  Un requisito implícito para que funcione el
método de mínimos cuadrados es que los
errores de cada medida estén distribuidos
de forma aleatoria.

5. MMC en Series de Tiempo
 Es el mejor método para obtener un ajuste
lineal a una serie de datos. Es base para la
identificación de componentes de tendencia
de una serie de tiempo.
 Con este método se encuentra la ecuación
de una recta de mínimos cuadrados. Con
esta recta se obtendrán los valores de
tendencia.

7. Cuatro componentes de una
serie de tiempo
 1. Tendencia secular o variación lineal
 2. Fluctuacion cíclica o variacion cíclica
 3. Variaci6n estacional
 4. Variaci6n irregular

8. Tendencia secular o lineal
 Representa la dirección a largo plazo de
la serie. Una manera de describir la
componente que corresponde a la
tendencia es ajustar visualmente una
recta a un conjunto de puntos de una
grafica.
 Para ser mas exactos con nuestros
pronósticos se utiliza el método de
mínimos cuadrados.

9. Existen tres razones por las cuales
resulta útil estudiar las tendencia
lineal:
 1. Nos permite describir un patrón histórico: Por
ejemplo, una universidad puede evaluar la efectividad
de un programa de captación de estudiantes
mediante el examen de sus tendencias en las
inscripciones anteriores.
 2. Nos permite proyectar patrones o tendencias
pasados al futuro: Por ejemplo, el examen de la tasa
de crecimiento de la población mundial puede ser de
ayuda para estimar la población en algún momento
futuro dado.
 3. Nos permite eliminar la componente de
tendencia de la serie: por ejemplo, la eliminación de
la componente de tendencia nos proporciona una
idea m:is precisa de la componente estacional.

10. Fórmulas:
Y=a+bx
Dónde:
 Y: Valor proyectado, estimado o pronóstico
de Y
 a: Punto dónde la recta corta el eje.
 b: La pendiente de la recta la tendencia.
 x: Cualquier valor de tiempo seleccionado

11.  b=nΣxy- Σx Σy
nΣx²- (Σx)²
 a= Σy -(b * Σx )
n n

12. Ejemplo:
Una zapatería que empezó
en 2006, la cual ha ido
aumentando sus ventas
año con año le gustaría
saber un aproximado de
sus ventas en el 2015.

13. Año Ventas
2006 $200,000
2007 $350,000
2008 $420,000
2009 $480,000
2010 $535,000
2011 $600,000
2012 $680,000
2013 $695,000
2014 $710,000

14. $900,000
$800,000
$700,000
$600,000
$500,000
$400,000
$300,000
$200,000
$100,000
$0
Ventas (Y)
2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
Ventas (Y)
Linear (Ventas (Y))

15. Solución:
Año (X) Ventas (Y) XY X²
2006 1 $200,000 $200,000 1
2007 2 $350,000 $700,000 4
2008 3 $420,000 $1,260,000 9
2009 4 $480,000 $1,920,000 16
2010 5 $535,000 $2,675,000 25
2011 6 $600,000 $3,600,000 36
2012 7 $680,000 $4,760,000 49
2013 8 $695,000 $5,560,000 64
2014 9 $710,000 $6,390,000 81
Total 45 $4,670,000 $27,065,000 285

16.  b=(9)(27,065,000)-(45)(4,670,000)
(9)(285)-(45)²
b=61,916.66
 a=4,670,000 –( 61,916.66 * 45 )
9 9
a=209,305.58

17. ¿Cuál es el pronóstico de las
ventas que habrá en 2015?
 Y= a+bx
 Y=209,305.58+(61,916.66)(x)
 Y=209,305.58+(61,916.66)(10)
Y= 828,472.18