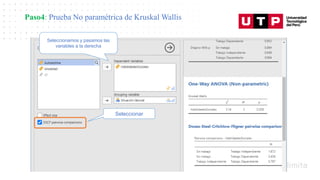
El documento presenta información sobre la prueba ANOVA y la prueba Kruskal Wallis para comparar más de dos grupos. La prueba ANOVA se utiliza cuando los datos cumplen los supuestos paramétricos de normalidad y varianzas iguales, mientras que la prueba Kruskal Wallis es la alternativa no paramétrica cuando los datos no cumplen dichos supuestos o son de nivel ordinal. El documento guía al lector a través de un ejemplo práctico para aplicar los procedimientos de estas pruebas estadísticas.

1. ESTADÍSTICA INFERENCIAL
PARA PSICOLOGÍA
Ciclo 5 - Unidad 3 - Semana 09
Sixto Salazar
c20230@utp.edu.pe

2. LOGRO DE LA SESIÓN
Finalizando la sesión, el estudiante identifica las fases del análisis
de diferencia de más de dos grupos. Aplica las pruebas Anova y
Kruskal Wallis. Valora su aplicación práctica para la generalización
de resultados.

3. ¿Qué vimos la clase pasada?

4. Repaso rápido…
https://app.sli.do/event/rw6ii1y2
www.slido.com
con el # 495434

5. Diferencia
de
grupos
(Coolican, 1997, p.458)
Ordinal
Intervalo
¿Satisface
supuestos
paramétricos?
Relacionado
No relacionado
• Prueba t muestras no relacionadas
• T de Welch
Rango de signo de Wilcoxon
Prueba U de Mann –Whitney
no
si
Pruebas
paramétricas
Pruebas
no
paramétricas
Relacionado
No relacionado
Prueba t muestras relacionadas
Recordando…

6. ¿Y si necesito comparar más de dos
grupos?

7. Datos/Observaciones
Tema
Prueba de ANOVA y Kruskal Wallis
¿Qué sabemos o qué podemos inferir del tema?

8. Pruebas estadísticas
Pruebas paramétricas Pruebas no paramétricas
Diferencia de 2 muestras
independientes
t de Student
t de Welch
U de Mann-Whitney
Diferencia de >2 muestras
independientes
ANOVA de una vía
ANOVA (Welch) de una vía
H de Kruskal-Wallis
Relación entre 2 variables r de Pearson rho de Spearman

9. Pruebas estadísticas y supuestos paramétricos
Cumple supuesto paramétrico
Prueba
(2 grupos)
Prueba
(>2 grupos)
Normalidad e Igualdad de varianza t de Student ANOVA de una vía
Normalidad y no Igualdad de varianza t de Welch
ANOVA de una vía
(Welch)
Sin normalidad U de Mann-Whitney Kruskal-Wallis
Normalidad r de Pearson ---
Sin normalidad rho de Spearman ---

10. Supuestos paramétricos Prueba estadística
Normalidad Shapiro–Wilk
Igualdad de varianzas (homocedasticidad) Levene
Supuestos paramétricos

11. Datos/Observaciones
Contraste de Hipótesis
Si p-valor > α (0.05) → No se rechaza la Ho
Si p-valor ≤ α (0.05) → Se rechaza la Ho
Recordando…

12. Datos/Observaciones
Contraste de Hipótesis
Si p-valor > α (0.05) → No se rechaza la Ho
→ Los resultados no son estadísticamente significativos
Si p-valor ≤ α (0.05) → Se rechaza la Ho
→ Los resultados son estadísticamente significativos
Recordando…

13. Datos/Observaciones
Prueba ANOVA de una vía
(paramétrica)

14. Datos/Observaciones
Prueba ANOVA de una vía
Objetivo: Compara más de dos grupos independientes (compara sus medias)
Es la generalización de la Prueba t Student para muestras no relacionadas o
independientes.
Por ejemplo, para…
Determinar si existe diferencias estadísticamente significativas en las puntuaciones de estrés, según
el área de trabajo (mantenimiento, producción y administrativos) en trabajadores de una empresa
de seguridad, 2020.

15. Datos/Observaciones
Requisitos
Se usa cuando…
Los datos (intervalo) cumplen los supuestos paramétricos
1. Normalidad
2. Igualdad de varianza (homogeneidad)
Prueba ANOVA de una vía

16. Datos/Observaciones
Prueba ANOVA de una vía
Hipótesis
H0 : ҧ
𝑥1 = ҧ
𝑥2 = ҧ
𝑥3 …
H1 : ҧ
𝑥1 ≠ ҧ
𝑥2 ≠ ҧ
𝑥3 …
H0 = Las medias entre los grupos son iguales.
H1 = Las medias entre algunos de los grupos son diferentes.

17. Datos/Observaciones
Vemos un ejemplo y practiquemos…
Determinar si existe diferencias estadísticamente significativas en las puntuaciones
de estrés, en trabajadores de una empresa de seguridad de Lima Metropolitana,
según el área de trabajo.
¿Cuál es la variable dependiente?
Base_clase
Abrir

18. Contraste de Hipótesis
Paso1: Plantear el sistema de hipótesis (alterna y nula)
Paso2: Establecer el nivel de significancia (α = 0.05)
Paso3: Comprobar supuesto paramétrico (normalidad e igualdad de varianza)
Paso4: Elegir el estadístico de prueba (paramétrica o no paramétrica)
Paso5: Dar lectura al p-valor calculado (α > p-valor >α ) Decisión
Paso6: Conclusión
(Supo, 2014, p.4)
Procedimiento para el contraste de hipótesis.

19. Paso1: Hipótesis de investigación
Ho: No existen diferencias estadísticamente significativas en las puntuaciones de estrés según el área
de trabajo.
H1: Existen diferencias estadísticamente significativas en las puntuaciones de estrés según el área de
trabajo.
Paso2: Nivel de significancia establecido: α = 0.05
Paso3: Comprobar supuestos paramétricos (normalidad)
3.1. Supuesto de normalidad
Ho: Los datos presentan distribución normal.
H1: Los datos no presentan distribución normal.

20. Datos/Observaciones
3.1. Supuesto de normalidad
Ruta: Analyses → Exploration → Descriptives
Seleccionar

21. Datos/Observaciones
3.1. Supuesto de normalidad
Seleccionar
Seleccionamos y pasamos las
variables a la derecha

22. Datos/Observaciones
3.1. Supuesto de normalidad
Seleccionar
¿Cumple o no el supuesto de normalidad?
Se verifica la normalidad de los datos a
la todos los grupos independientes

23. Datos/Observaciones
3.1. Supuesto de normalidad
Resumir
Lectura: p-valor = 0.257 – 0.869
Contraste: p-valor > 0.05
Decisión: No se rechaza la Ho
Conclusión: Los resultados de la prueba Shapiro-Wilk
muestra valores de p-valor (0.257 – 0.869) mayores al
nivel de significancia (0.05); por lo tanto, los resultados
no son estadísticamente significativos para rechazar la
Ho y se concluye que los datos presentan distribución
normal.

24. Paso3: Comprobar supuesto
Paso 3.2. Comprobar supuesto de igualdad de varianzas (prueba de Levene)
Ho: Los grupos presentan varianzas iguales
H1: Los grupos no presentan varianzas iguales
El p-valor de igualdad de varianzas se muestra conjuntamente con los
resultados de ANOVA

25. Paso 3.2. Comprobar supuesto de igualdad de varianzas (prueba de Levene)
Ruta: Analyses → ANOVA → One-Way ANOVA
Seleccionar

26. Paso 3.2. Comprobar supuesto de igualdad de varianzas (prueba de Levene)
Ingresamos las variables
Seleccionar
¿Cumple el supuesto de
igualdad de varianzas?

27. Paso 3.2. Comprobar supuesto de igualdad de varianzas (prueba de Levene)
Lectura: p-valor = 0.3
Contraste: p-valor > 0.05
Decisión: No se rechaza la Ho
Conclusión: Los resultados de la prueba Levene muestra
un p-valor (0.3) mayor al nivel de significancia (0.05);
por lo tanto, los resultados no son estadísticamente
significativos para rechazar la Ho y se concluye que los
grupos presentan varianzas iguales.

28. Paso3: Cumplen los supuestos paramétricos (normalidad y varianzas)
3.1. Supuesto de normalidad: Se comprueba el supuesto de normalidad en los grupos.
3.2. Supuesto de igualdad de varianza: Se comprueba el supuesto de igualdad de varianza en los
grupos.
Paso4: Elegir el estadístico de prueba (paramétrica o no paramétrica)
Al cumplirse ambos supuestos paramétricos corresponde usar una prueba paramétrica. Por lo tanto,
se usará la prueba de ANOVA.

29. Paso4: Prueba ANOVA
Ruta: Analyses → ANOVA → One-Way ANOVA
Seleccionar

30. Paso4: Prueba ANOVA
Seleccionar, porque se
asumen varianzas iguales
Seleccionar
Seleccionar

31. Paso4: Prueba ANOVA
Seleccionar para ver los resultados de la
comparación los grupos independientes
por pares
Seleccionar, porque se
asumen varianzas iguales

32. Paso4: Prueba ANOVA
Lectura: p-valor = 0.001
Contraste: p-valor < 0.05
Decisión: Se rechaza la Ho
Ho: No existen diferencias estadísticamente significativas en las
puntuaciones de estrés según el área de trabajo.
H1: Existen diferencias estadísticamente significativas en las
puntuaciones de estrés según el área de trabajo.
¿Todos los grupos son diferentes? ¿cuál es la diferencia entre cada
grupo?

33. Paso4: Prueba ANOVA
¿Qué notamos?

34. Paso4: Prueba ANOVA
Son los resultados de la prueba T Student para cada par de grupos.

35. Paso6: Conclusión
Descriptivo
El estudio realizado con una muestra de 200 participantes, halló promedios de estrés similares en las
áreas de control de calidad (35) y administrativos (34.9), diferenciándose de las áreas de producción
(31.9) y mantenimiento (32.6). La prueba ANOVA muestra un p-valor (0.001) menor al nivel de
significancia (0.05); es decir, existe evidencia suficiente para rechazar la hipótesis nula. Por lo tanto, la
media de estrés es estadísticamente diferente en las áreas de trabajo.
Conclusión
Se encontró mayor estrés en las áreas de control de calidad y administrativos, y menor estrés en las áreas
de producción y mantenimiento.

36. Datos/Observaciones
Prueba ANOVA de Welch
(paramétrica)

37. Paso 3.2. Comprobar supuesto de igualdad de varianzas (prueba de Levene)
0.016
Suponiendo que no se cumple el supuesto de igualdad de varianzas

38. Paso4: Prueba ANOVA
Ruta: Analyses → ANOVA → One-Way ANOVA
Seleccionar

39. Paso4: Prueba ANOVA
Seleccionar
Seleccionar
Seleccionar, porque no se
asumen varianzas iguales

40. Paso4: Prueba ANOVA
Seleccionar, porque no se
asumen varianzas iguales

41. Paso4: Prueba ANOVA
Se interpretan los resultados igual que el ANOVA

42. Paso4: Prueba ANOVA

43. Datos/Observaciones
Prueba Kruskal Wallis
(No paramétrica)

44. Datos/Observaciones
Prueba Kruskal Wallis
Objetivo: Compara más de dos grupos independientes (compara sus medianas)
Es la versión no paramétrica de la Prueba ANOVA para muestras no relacionadas o independientes.
Por ejemplo, para…
Determinar si existe diferencias estadísticamente significativas en las puntuaciones de estrés, según
el área de trabajo (mantenimiento, producción y administrativos) en trabajadores de una empresa
de seguridad, 2020.

45. Datos/Observaciones
Requisitos
Se usa cuando…
Los datos (intervalo) NO cumplen el supuesto paramétrico
1. Normalidad
O cuando los datos son de nivel ordinal
Prueba Kruskal Wallis

46. Datos/Observaciones
Hipótesis
H0 : Me1 = Me2 = Me3…
H1 : Me1 ≠ Me2 ≠ Me3. . .
H0 = Las medianas entre los grupos son iguales.
H1 = Las medianas entre algunos de los grupos son diferentes.
Prueba Kruskal Wallis

47. Datos/Observaciones
Vemos un ejemplo y practiquemos…
¿Cuál es la variable dependiente?
Base_clase2
Abrir
Determinar si existe diferencias estadísticamente significativas en las puntuaciones
de Habilidades sociales, en pobladores del distrito de SMP, según su situación
laboral.

48. Contraste de Hipótesis
Paso1: Plantear el sistema de hipótesis (alterna y nula)
Paso2: Establecer el nivel de significancia (α = 0.05)
Paso3: Comprobar supuesto paramétrico (normalidad e igualdad de varianza)
Paso4: Elegir el estadístico de prueba (paramétrica o no paramétrica)
Paso5: Dar lectura al p-valor calculado (α > p-valor >α ) Decisión
Paso6: Conclusión
(Supo, 2014, p.4)
Procedimiento para el contraste de hipótesis.

49. Paso1: Hipótesis de diferencia de medias
Ho: No existen diferencias estadísticamente significativas en las puntuaciones de habilidades sociales
según la situación laboral.
H1: Existen diferencias estadísticamente significativas en las puntuaciones de habilidades sociales según
la situación laboral.
Paso2: Nivel de significancia establecido: α = 0.05
Paso3: Comprobar supuesto paramétrico
3.1. Supuesto de normalidad
Ho: Los datos presentan distribución normal.
H1: Los datos no presentan distribución normal.

50. Datos/Observaciones
3.1. Supuesto de normalidad
Ruta: Analyses → Exploration → Descriptives
Seleccionar

51. Datos/Observaciones
3.1. Supuesto de normalidad
Seleccionamos y pasamos las
variables a la derecha
Seleccionar

52. Datos/Observaciones
3.1. Supuesto de normalidad
Seleccionar
¿Se cumple el supuesto?

53. Datos/Observaciones
3.1. Supuesto de normalidad
Resumir
Lectura: p-valor = 0.048 – 0.094
Contraste: Un p-valor < 0.05
Decisión: No se rechaza la Ho
Conclusión: Los resultados de la prueba Shapiro-Wilk
muestra valores de p-valor (0.048 – 0.094) mayores al
nivel de significancia (0.05); sin embargo, el grupo de
trabajo independiente presenta un p-valor (0.048) menor.
Por lo tanto, se concluye que los datos presentan
distribución normal.

54. Paso3: Supuestos paramétricos
3.1. Supuesto de normalidad: No se comprueba el supuesto de normalidad en los grupos.
Paso4: Elegir el estadístico de prueba (paramétrica o no paramétrica)
Al no cumplirse el supuesto paramétrico de normalidad corresponde usar una prueba no paramétrica.
Por lo tanto, se usará la prueba Kruskal Wallis.

55. Datos/Observaciones
Paso4: Prueba No paramétrica de Kruskal Wallis
Ruta: Analyses → ANOVA → One-Way ANOVA Kruskal-Wallis
Seleccionar

56. Datos/Observaciones
Paso4: Prueba No paramétrica de Kruskal Wallis
Seleccionamos y pasamos las
variables a la derecha
Seleccionar

57. Datos/Observaciones
Paso4: Prueba No paramétrica de Kruskal Wallis
Lectura: p-valor = 0.208
Contraste: p-valor > 0.05
Decisión: No se rechaza la Ho
Ho: No existen diferencias estadísticamente significativas en las
puntuaciones de estrés según la situación laboral.
H1: Existen diferencias estadísticamente significativas en las
puntuaciones de estrés según la situación laboral.
¿Ningún grupo es diferente? ¿cuál es la diferencia entre cada
grupo?

58. Datos/Observaciones
Paso4: Prueba No paramétrica de Kruskal Wallis
Son los resultados de la prueba U de Mann –Whitney para cada par de grupos.

59. Paso6: Conclusión
Descriptivo
El estudio realizado con una muestra de 115 participantes, halló medianas similares en los tres grupos de
estudio de situación laboral. La prueba Kruskal Wallis muestra un p-valor (0.208) mayor al nivel de
significancia (0.05); es decir, no existe evidencia suficiente para rechazar la hipótesis nula. Por lo tanto,
las medianas de habilidades sociales no son estadísticamente diferentes a la situación laboral.
Conclusión
Las personas de trabajo independiente, trabajo dependiente y sin trabajo, muestran similares habilidades
sociales.

60. Actividad S09
En CANVAS encontrarán como TAREA una
actividad para desarrollar en grupos.
Plazo de entrega jueves 02 de junio hasta las
11:59pm

61. Indicaciones para las respuestas
1. Redactar las hipótesis de investigación; alterna y nula (no las de los supuestos paramétricos).
2. Colocar los resultados de los supuestos paramétricos, los p-valor (normalidad e igualdad de varianzas) y redactar solo la
conclusión general; se cumplen o no los supuestos paramétricos. Indicar qué prueba estadística se usará.
3. Colocar los resultados de la prueba estadística elegida (p-valor). Además de la media o mediana, según sea el caso.
4. Interpretar los resultados de la prueba estadística elegida, interpretación “descriptiva” semejante a lo visto en sesión, pero no
igual, redactar de manera diferente (amplio).
5. Redactar una “conclusión” también semejante a lo visto en sesión, pero no igual, redactar de manera diferente (breve).

62. REFERENCIAS
Coolican, H. (1997). Métodos de investigación y estadística en psicología. México: Manual
moderno.

63. GRACIAS
C20230@utp.edu.pe