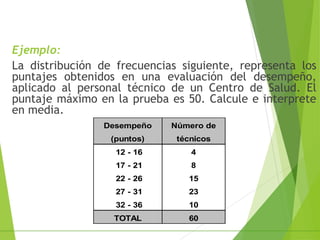
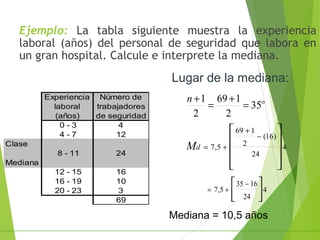
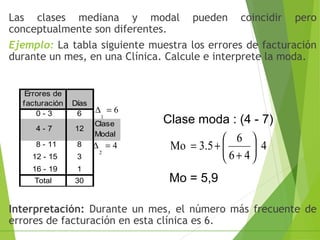
Este documento describe tres medidas de tendencia central para datos agrupados: la media, la mediana y la moda. Explica cómo calcular cada una a partir de tablas de frecuencias, incluyendo fórmulas y ejemplos. También discute las ventajas y desventajas de cada medida.

1. MEDIDAS DE TENDENCIA CENTRAL PARAMEDIDAS DE TENDENCIA CENTRAL PARA
DATOS AGRUPADOSDATOS AGRUPADOS.

2. 1. Diferenciar los diversos tipos de medidas de
resumen que se pueden aplicar a un conjunto de
datos agrupados.
2. Calcular e interpretar las principales medidas de
tendencia central para datos agrupados.
Al finalizar la Tema, el participante será capaz de:
OBJETIVOS

3. CONTENIDO
Principales medidas de tendencia central para
datos agrupados.
 Medias
 Mediana
 Moda

4. La Media aritmética
Cálculo a partir de datos agrupados.
El cálculo de la media aritmética, cuando los
datos disponibles se encuentran en tablas de
distribución de frecuencias, se realiza utilizando
la formula siguiente
donde: :media muestral
:frecuencia absoluta de la clase i
:marca de la clase i
∑
∑
=
== n
f
n
f
i
i
i
ii
x
1
1
X
x
if
iX

5. Ejemplo:
La distribución de frecuencias siguiente, representa los
puntajes obtenidos en una evaluación del desempeño,
aplicado al personal técnico de un Centro de Salud. El
puntaje máximo en la prueba es 50. Calcule e interprete
en media.
Desempeño Número de
(puntos) técnicos
12 - 16 4
17 - 21 8
22 - 26 15
27 - 31 23
32 - 36 10
TOTAL 60

6. Primero se calcularán las marcas de clase ( );
es decir, el valor intermedio de cada clase
Marca de Frecuencia
clase ( ) absoluta(fi)
12 - 16 14 4
17 - 21 19 8
22 - 26 24 15
27 - 31 29 23
32 - 36 34 10
Total 60
14(4) + 19 (8) + 24 (15) + 29 (23) + 34 (10)
4 + 8 + 15 + 23 + 10
iX
ix
=x =x
=x
clase
1575
60
26.25

7. Interpretación: Si se elige al azar a
un trabajador técnico de este
hospital, se espera que tenga un
puntaje de 26,25 en su evaluación de
desempeño.

8. d) Cálculo a partir de datos agrupados.
donde:
:
mediana
: limite real (o frontera) inferior de la clase
mediana.
: número total de datos.
: suma de todas las frecuencias hasta, pero
sin incluir, la clase mediana.
: frecuencia de la clase mediana
: amplitud de clase
( )
c
Mdf
F
n
Md i










+−
+
+=
1
2
1
L
Md
iL
n
F
Mdf
c

9. Ejemplo: La tabla siguiente muestra la experiencia
laboral (años) del personal de seguridad que labora en
un gran hospital. Calcule e interprete la mediana.
Experiencia Número de
laboral trabajadores
(años) de seguridad
0 - 3 4
4 - 7 12
Clase
Mediana
8 - 11 24
12 - 15 16
16 - 19 10
20 - 23 3
69
Lugar de la mediana:
4
24
)16(
2
169
5,7









 −
+
+=dM
4
24
1635
5,7



 −
+=
Mediana = 10,5 años
o
35
2
169
2
1
=
+
=
+n

10. Interpretación:
La mitad del personal de seguridad
que labora en este hospital tienen una
experiencia laboral igual o menor a 10
años 6 meses. La otra mitad de este
personal tiene una experiencia laboral
igual o mayor a 10 años y 6 meses.

11. Ventajas y desventajas
Ventajas:
Los valores extremos no afectan a la mediana como en el caso de la media
aritmética.
Es fácil de calcular, interpretar y entender.
Se puede determinar para datos cualitativos, registrados bajo una escala
ordinal.
Desventajas:
Como valor central, se debe ordenar primero la serie de datos.
Para una serie amplia de datos no agrupados, el proceso de ordenamiento de
los datos demanda tiempo y usualmente provoca equivocaciones.

12. La Moda
Cálculo a partir de datos agrupados
donde:
: moda
: limite real (o frontera) inferior de la clase
modal (la de mayor frecuencia)
: frecuencia de la clase modal menos la
frecuencia de la clase anterior
: frecuencia de la clase modal menos la
frecuencia de la clase siguiente
: amplitud de clase
c
i 





∆+∆
∆
+=
21
1
LoM
oM
i
L
1
∆
2
∆
c

13. Las clases mediana y modal pueden coincidir pero
conceptualmente son diferentes.
Ejemplo: La tabla siguiente muestra los errores de facturación
durante un mes, en una Clínica. Calcule e interprete la moda.
Interpretación: Durante un mes, el número más frecuente de
errores de facturación en esta clínica es 6.
Errores de
facturación Días
0 - 3 6
4 - 7 12
Clase
Modal
8 - 11 8
12 - 15 3
16 - 19 1
Total 30
Clase moda : (4 - 7)
Mo = 5,9
6
1
=∆
4
2
=∆ 4
46
6
5.3Mo 





+
+=

14. Ventajas y desventajas de la moda.
Ventajas:
Se puede utilizar tanto para datos cualitativos
como cuantitativos.
No se ve afectada por los valores extremos.
Se puede calcular, a pesar de que existan una o
más clases abiertas.
Desventajas:
No tiene un uso tan frecuente como la media.
Muchas veces no existe moda (distribución
amodal).
En otros casos la distribución tiene varias
modas, lo que dificulta su interpretación.