Este documento describe los operadores lógicos de álgebra Booleana, incluyendo AND, OR, NOT, NAND, NOR, EXOR y EXNOR. Define sus símbolos, tablas de verdad, circuitos equivalentes y diagramas de tiempos. También cubre las propiedades de conmutatividad, asociatividad y distributividad de estos operadores, así como ejercicios para evaluar expresiones lógicas.

1. Álgebra Booleana

2. Operadores Lógicos
•And
•Or
•Not
•Nand
•Nor
•Exor
•Exnor
• Nombre
• Característica
• Símbolo
• Expresión Matemática
• Tabla de verdad
• Circuito Equivalente
• Diagrama de Tiempos

3. Nombre AND OR NOT
Característica Condición Alternativa Negar
Símbolo
Expresión
Matemática S=AB S=A+B S=A
Tabla de
Verdad
Circuito
eléctrico
equivalente
Diagrama
de
Tiempos
? ? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?

4. Ejercicio 1
a que operación booleana se refiere el enunciado
La salida es cero cuando cualquier
entrada es igual a cero
A B

5. Cualquier entrada uno produce una salida uno.
Ejercicio 2
a que operación booleana se refiere el enunciado
A + B

6. solamente cuando todas las entradas son cero
producen una salida cero.
Ejercicio 3
a que operación booleana se refiere el enunciado
A + B

7. La salida es uno solamente cuando todas las
entradas son uno.
Ejercicio 4 a que operación booleana
se refiere el enunciado

8. La salida es siempre lo contrario de la entrada.
Ejercicio 5 a que operación booleana
se refiere el enunciado
m A S
0 0 1
1 1 0

9. NAND
La operación Nand es el negado de
la salida de la operación And.

10. La operación Nand es el negado de
las entradas de la operación OR.
NAND

11. Tabla de verdad
m A B AB
0 0 0 1
1 0 1 1
2 1 0 1
3 1 1 0
NAND

12. Circuito Eléctrico equivalente
m A B AB
0 0 0 1
1 0 1 1
2 1 0 1
3 1 1 0
NAND

13. Nand de
3 entradas
F(A, B, C) = A B C
m A B C ABC
0 0 0 0 1
1 0 0 1 1
2 0 1 0 1
3 0 1 1 1
4 1 0 0 1
5 1 0 1 1
6 1 1 0 1
7 1 1 1 0

15. La operación Nor es el negado de
la salida de la operación OR.
NOR

16. La operación Nor es el negado de
las entradas de la operación AND.
NOR

17. Tabla de Verdad
m A B A+B
0 0 0 1
1 0 1 0
2 1 0 0
3 1 1 0
NOR
X = A +B

18. Circuito eléctrico equivalente
m A B A+B
0 0 0 1
1 0 1 0
2 1 0 0
3 1 1 0
NOR

19. NOR de tres
entradas
m A B C A+B+C
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 0 1 1 0
4 1 0 0 0
5 1 0 1 0
6 1 1 0 0
7 1 1 1 0
F(A, B, C) = A+B+C

21. Alternativa Exclusiva
(Opción entre dos cosas, una, otra pero no ambas)
EXOR
La operación Exor produce un resultado 1,
cuando un número impar de variables de entrada valen 1.

22. A⊕
B
EXOR

23. A⊕
B
EXOR

24. Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.
m A B C X
0 0 0 0
1 0 0 1
2 0 1 0
3 0 1 1
4 1 0 0
5 1 0 1
6 1 1 0
7 1 1 1

25. m A B C X
0 0 0 0
1 0 0 1 1
2 0 1 0
3 0 1 1
4 1 0 0
5 1 0 1
6 1 1 0
7 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

26. m A B C X
0 0 0 0
1 0 0 1 1
2 0 1 0 1
3 0 1 1
4 1 0 0
5 1 0 1
6 1 1 0
7 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

27. m A B C X
0 0 0 0
1 0 0 1 1
2 0 1 0 1
3 0 1 1
4 1 0 0 1
5 1 0 1
6 1 1 0
7 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

28. m A B C X
0 0 0 0
1 0 0 1 1
2 0 1 0 1
3 0 1 1
4 1 0 0 1
5 1 0 1
6 1 1 0
7 1 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

29. m A B C X
0 0 0 0
1 0 0 1 1
2 0 1 0 1
3 0 1 1
4 1 0 0 1
5 1 0 1
6 1 1 0
7 1 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

30. m A B C X
0 0 0 0 0
1 0 0 1 1
2 0 1 0 1
3 0 1 1 0
4 1 0 0 1
5 1 0 1 0
6 1 1 0 0
7 1 1 1 1
Exor , produce un resultado 1,
cuando un número impar de
Variables de entrada valen 1.

31. Exor
produce un resultado 1, cuando
un número impar
de variables de entrada valen 1.
m A B C D X
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
12 1 1 0 0
13 1 1 0 1
14 1 1 1 0
15 1 1 1 1
X = A ⊕ B ⊕ C ⊕
D

32. Exor
produce un resultado 1, cuando
un número impar
de variables de entrada valen 1.
m A B C D X
0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 1
3 0 0 1 1
4 0 1 0 0 1
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1 1
8 1 0 0 0 1
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1 1
12 1 1 0 0
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1
X = A ⊕ B ⊕ C ⊕
D

33. Exor
produce un resultado 1, cuando
un número impar
de variables de entrada valen 1.
m A B C D X
0 0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 1
3 0 0 1 1 0
4 0 1 0 0 1
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 1
8 1 0 0 0 1
9 1 0 0 1 0
10 1 0 1 0 0
11 1 0 1 1 1
12 1 1 0 0 0
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1 0
X = A ⊕ B ⊕ C ⊕
D

35. La operación Exnor es el negado de la salida
de la operación Exor.
A⊕
B
A
B
EXNOR

36. Condición Alternativa Impar
Negado de
And
Negado de
Exor
Negado de
Or
m A B C And Or Exor Nand Ex-Nor Nor
0 0 0 0 0 0 0 1 1 1
1 0 0 1 0 1 1 1 0 0
2 0 1 0 0 1 1 1 0 0
3 0 1 1 0 1 0 1 1 0
4 1 0 0 0 1 1 1 0 0
5 1 0 1 0 1 0 1 1 0
6 1 1 0 0 1 0 1 1 0
7 1 1 1 1 1 1 0 0 0

37. Leyes y teoremas del álgebra Booleana

38. Leyes y teoremas del álgebra Booleana

39. Leyes y teoremas del álgebra Booleana

40. Leyes y teoremas del álgebra Booleana

41. Leyes y teoremas del álgebra Booleana

42. Leyes y teoremas del álgebra Booleana

43. Leyes y teoremas del álgebra Booleana

44. Leyes y teoremas del álgebra Booleana

45. a) 1*1= 1
Evaluar las siguiente Operación

46. b) 0*0 =0
Evaluar las siguiente Operación

47. c) 1*0*0 = 0
Evaluar las siguiente Operación

48. c) 1*A*0 = 0
Evaluar las siguiente Operación

49. Leyes y teoremas del álgebra Booleana

50. Leyes y teoremas del álgebra Booleana

51. Leyes y teoremas del álgebra Booleana

52. Leyes y teoremas del álgebra Booleana

53. Leyes y teoremas del álgebra Booleana

54. Leyes y teoremas del álgebra Booleana

55. Leyes y teoremas del álgebra Booleana

56. Leyes y teoremas del álgebra Booleana

57. Evaluar las siguiente operación
a) 1+1=1

58. a) 1+0 =1
Evaluar las siguiente operación

59. a)0+0+0 =0
Evaluar las siguiente operación

60. Leyes y teoremas del álgebra Booleana

61. And y Nand
1

62. A
And y Nand

63. A
And y Nand

64. 1
And y Nand

65. Or y Nor
A

66. 0
Or y Nor

67. A
Or y Nor

68. 0
Or y Nor

69. Resuelva las siguientes proposiciones
1.- A ⊕ 0
=
2.- A ⊕ 1
=
3.- A ⊕ A
5.- A ⊕ 0
=
6.- A ⊕ 1
=
7.- A ⊕ A

70. Propiedades
•Conmutativa
•Asociativa
•Distributiva

71. Conmutativa
AND

72. Conmutativa
Or
A+B = B+A

73. Conmutativa
Exor
A⊕B =
B⊕A

74. Conmutativa

75. Asociativa
And A(B C) = (A B) C = A B C

76. Asociativa
(A B) C = A B C

77. Asociativa
Or A+(B+C) = (A+B)+C = A+B+C
Exor A⊕(B⊕C) = (A⊕B)⊕C =
A⊕B⊕C
And A(B C) = (A B) C = A B C

78. Asociativa
Or A+B+C+D

79. Asociativa
Or (A+B)+C+D = (A+B)+(C+D)
Or A+B+C+D

80. Asociativa
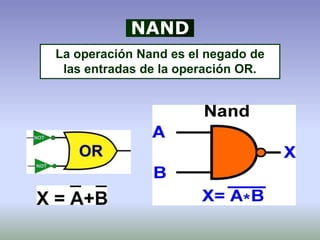
Nand [A(B C)’]’ ≠ [(A B)’ C]’ ≠ (A B C)’
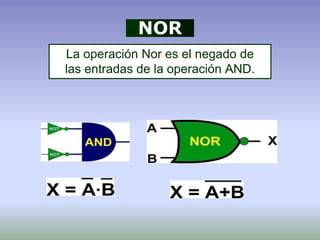
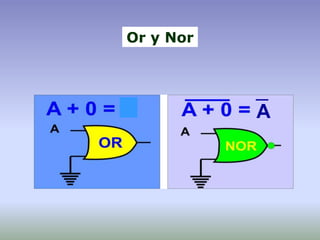
Nor [A+(B+C)’]’ ≠ [(A+B)’+C]’≠ (A+B+C)’
Enxor [A⊕(B⊕C)’]’ ≠ [(A ⊕ B)’⊕C]’≠
(A⊕B⊕C)’

81. Asociativa

82. Distributiva

83. Distributiva

84. A + AC + AB + BC
Distributiva
AA + AC + AB + BC
A + AC + AB + BC
A (1+C+B)+ BC
A*1+ BC
A+ BC = A+ BC

85. Distributiva

87. Resuelva las siguientes proposiciones
1.- A ⊕ 0
=
2.- A ⊕ 1
=
3.- A ⊕ A
=