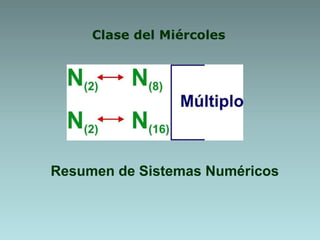
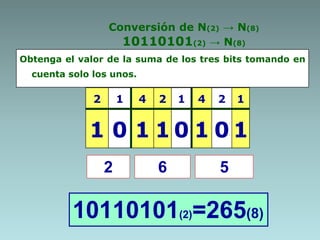
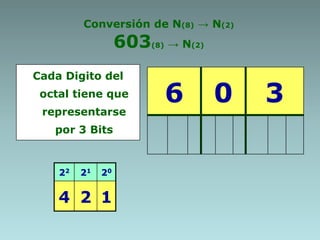
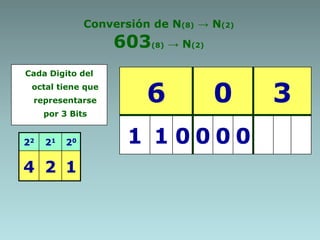
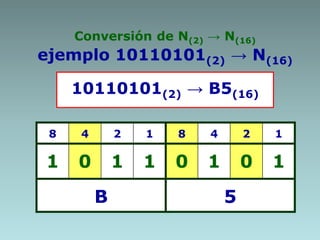
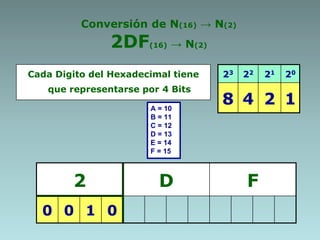
Este documento describe métodos para convertir números entre diferentes sistemas numéricos. Explica cómo convertir números decimales a binarios, octales y hexadecimales usando extracción de potencias o residuos. También cubre cómo convertir entre sistemas binarios, octales y hexadecimales usando propiedades de múltiplos de potencias de la base. Proporciona ejemplos detallados de cada conversión.

1. Conversiones entre sistemas
numéricos

2. Extracción de potencias.
Para números con decimales
Este método consiste en tres pasos
Primero elaborar una tabla de potencias de la base a la cual se va a
convertir el número decimal.
Segundo restar sucesivamente al numero en base diez la potencia igual
o próxima menor hasta que la diferencia sea igual a cero.
Tercer con las potencias utilizadas en la resta formar el numero.

3. Ejemplo 1 convertir un numero decimal a binario
25.5(10) → N(2)
2-2 .25
2-1 .5
20 1
21 2
22 4
23 8
24 16
25 32
1.- Tabla de potencias
En donde el rango de valores asignado a la
tabla para efectuar la resta deberá cubrir de
un valor menor a 0.5 que representa la parte
mas pequeña de numero 25.5 la potencia
requerida es 2-2 = 0.25 y un valor mayor a 25
como 25 = 32.

4. 25.5(10) → N(2)
2-2 .25
2-1 .5
20 1
21 2
22 4
23 8
24 16
25 32
1.- Tabla de potencias
25.5
2.- Restar sucesivamente
16.0 24
9.5
8.0 23
1.5
1.0 20
0.5
0.5 2-1
0.0

5. 25.5(10) → N(2)
2-2 .25
2-1 .5
20 1
21 2
22 4
23 8
24 16
25 32
1.- Tabla de potencias 2.- Restar sucesivamente 3.- Formar el numero
4 3 2 1 0 -1
1 1 0 0 1 1
25.5(10)=11001.1(2
)
25.5
16.0 24
9.5
8.0 23
1.5
1.0 20
0.5
0.5 2-1
0.0

6. Ejemplo 2: 25.5(10) → N(8)
8-1 .125
80 1
81 8
82 64
1.- Tabla de potencias
25.5
2.- Restar sucesivamente
24.0 3 veces 81
1.5
1.0 80
0.5
0.5 4 veces 8-1
0.0

7. Ejemplo 2: 25.5(10) → N(8)
8-1 .125
80 1
81 8
82 64
1.- Tabla de potencias
25.5
2.- Restar sucesivamente
24.0 3 veces 81
1.5
1.0 80
0.5
0.5 4 veces 8-1
0.0
3.- Formar el numero
1 0 -1
3 1
25.5(10)=31.4(8)
4

8. Ejemplo 3: 27.5(10) → N(16)
16-1 .0625
160 1
161 16
162 256
1.- Tabla de potencias

9. Ejemplo 3: 27.5(10) → N(16)
16-1 .0625
160 1
161 16
162 256
1.- Tabla de potencias
27.5
2.- Restar sucesivamente
16.0 161
11.5
11.0 11 veces 160
0.5
0.5 8 veces 16-1
0.0

10. Ejemplo 3 27.5(10) → N(16)
16-1 .0625
160 1
161 16
162 256
1.- Tabla de potencias
27.5
2.- Restar sucesivamente
16.0 161
11.5
11.0 11 veces 160
0.5
0.5 8 veces 16-1
0.0
3.- Formar el numero
1 0 -1
1 B
27.5(10)=1B.8(16)
8

11. Ejemplo 4: 16.5(10) → N(16)
16-1 .0625
160 1
161 16
162 256
1.- Tabla de potencias
16.5
2.- Restar sucesivamente
16.0 161
0.5
0.5 8 veces 16-1
0.0
3.- Formar el numero
1 0 -1
1 0
16.5(10)=10.8(16)
8

12. Realice la siguiente Actividad
27.6(10) → N(5)
5-1 .2
50 1
51 5
52 25
1.- Tabla de potencias 2.- Restar sucesivamente 3.- Formar el numero
2 1 0 -1
1 2
27.6(10)=102.3(5)
30

13. Conversiones entre sistemas
numéricos

14. Residuos
Este método consiste en dividir sucesivamente el
numero decimal entre la base a la que se desee
convertir hasta que el cociente sea menor que la
base.
El numero equivalente se forma con el ultimo
cociente y los residuos.
N(10) → N(X)

15. Ejemplo 1:
convertir un numero decimal a binario
35 (10) → N(2)
35 2
171LSB 2
81 2
40 2
20 2
1
0 MSB
100011(2)

16. Ejemplo 2
convertir un numero decimal a octal
85 (10) → N(8)
85 8
105LSD 8
1
2
MSD
125(8)

17. Ejemplo 3
convertir un numero decimal a Hexadecimal
46 (10) → N(16)
46 16
214LSD
MSD
2E(16)
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

18. Ejemplo 4
convertir un numero decimal a base 5
47 (10) → N(5)
47 5
92LSD
MSD
142(5)
5
1
4

19. Ejemplo 5
convertir un numero decimal a base 7
47 (10) → N(7)
65(7)

20. Realice la siguiente Actividad
47 (8) → N(16)
27(16)
N(x) → N(10) Multiplicar por la base y sumar
N(10) → N(X) Residuos

21. Clase del Miércoles
Resumen de Sistemas Numéricos

22. Múltiplo en potencia
La relación que existe entre la base dos y la
base ocho es de 3 ya que 23 = 8.
de la misma forma entre la base dos y el
Hexadecimal es de 4 ya que 24 = 16.
N(2) ↔ N(8) R=3
N(2) ↔ N(16) R=4

23. Ejemplo 1
Conversión de N(2) → N(8)
1 0 1 1 0 1 0 1(2) → N(8)
Separe de en grupos de tres bits iniciando con
la de menor peso, como lo indica la figura.
N(2) ↔ N(8) R=3 23=8

24. Ejemplo 1
Conversión de N(2) → N(8)
10110101(2) → N(8)
De el valor de 1 2 y 4 a cada digito correspondiente
como lo muestra la figura.
1 0 1 1 0 1 0 1
12412412

25. Conversión de N(2) → N(8)
10110101(2) → N(8)
Obtenga el valor de la suma de los tres bits tomando en
cuenta solo los unos.
2 1 4 2 1 4 2 1
1 0 1 1 0 1 0 1
562
10110101(2)=265(8)

26. 1010000101(2)= 1205(8)
Realice la siguiente Actividad
convertir un número binario a octal
1010000101 (2)→ N(8)

27. Conversión de N(8) → N(2)
603(8) → N(2)
Cada Digito del
octal tiene que
representarse
por 3 Bits
6 0 3
22 21 20
4 2 1

28. Conversión de N(8) → N(2)
603(8) → N(2)
Cada Digito del
octal tiene que
representarse
por 3 Bits
6 0 3
22 21 20
4 2 1

29. Conversión de N(8) → N(2)
603(8) → N(2)
Cada Digito del
octal tiene que
representarse
por 3 Bits
6 0 3
1 1 022 21 20
4 2 1

30. Conversión de N(8) → N(2)
603(8) → N(2)
Cada Digito del
octal tiene que
representarse
por 3 Bits
6 0 3
1 1 0 0 0 022 21 20
4 2 1

31. Conversión de N(8) → N(2)
603(8) → N(2)
Cada Digito del
octal tiene que
representarse
por 3 Bits
6 0 3
1 1 0 0 0 0 0 1 122 21 20
4 2 1
603(8)=110000011(2)

32. 4172(8)= 100001111010(2)
Realice la siguiente Actividad
convertir un número octal a binario
4172 (8)→ N(2)
22 21 20
4 2 1

33. Conversión de N(2) → N(16)
ejemplo 10110101(2) → N(16)
Separe de en grupos de cuatro bits iniciando con la
de menor peso, como lo indica la figura.
1 0 1 1 0 1 0 1

34. Conversión de N(2) → N(16)
ejemplo 10110101(2) → N(16)
Separe de en grupos de cuatro bits iniciando con la
de menor peso, como lo indica la figura.
1 0 1 1 0 1 0 1

35. Conversión de N(2) → N(16)
ejemplo 10110101(2) → N(16)
De el valor de 1, 2, 4 y 8 a cada digito
correspondiente como lo muestra la figura.
1 0 1 1 0 1 0 1
12481248

36. Obtenga el valor de la suma de los cuatro
bits tomando en cuenta solo los unos.
8 4 2 1 8 4 2 1
1 0 1 1 0 1 0 1

37. 8 4 2 1 8 4 2 1
1 0 1 1 0 1 0 1
5
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

38. Conversión de N(2) → N(16)
ejemplo 10110101(2) → N(16)
10110101(2) → B5(16)
8 4 2 1 8 4 2 1
1 0 1 1 0 1 0 1
B 5

39. 10101100(2)= AC(16)
Realice la siguiente Actividad
convertir un número Binario a Hexadecimal
10101100 (2)→ N(16)
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

40. Conversión de N(16) → N(2)
2DF(16) → N(2)
Cada Digito del Hexadecimal tiene
que representarse por 4 Bits
23 22 21 20
8 4 2 1
2 D F
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

41. Conversión de N(16) → N(2)
2DF(16) → N(2)
Cada Digito del Hexadecimal tiene
que representarse por 4 Bits
23 22 21 20
8 4 2 1
2 D F
0 0 1 0
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

42. Conversión de N(16) → N(2)
2DF(16) → N(2)
Cada Digito del Hexadecimal tiene
que representarse por 4 Bits
23 22 21 20
8 4 2 1
2 D F
0 0 1 0 1 1 0 1
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

43. Conversión de N(16) → N(2)
2DF(16) → N(2)
Cada Digito del Hexadecimal tiene
que representarse por 4 Bits
23 22 21 20
8 4 2 1
2 D F
0 0 1 0 1 1 0 1 1 1 1 1
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

44. Conversión de N(16) → N(2)
2DF(16) → N(2)
Cada Digito del Hexadecimal tiene que representarse
por 4 Bits
2DF(16) → 1011011111(2)

45. 5BC(16)= 10110111100(2)
Realice la siguiente Actividad
convertir un número Hexadecimal a Binario
5BC (16)→ N(2)
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15
23 22 21 20
8 4 2 1

46. Conversiones entre sistemas
numéricos

47. Ejemplo 1 convertir un número binario N(2)
a N(8), N(10), N(16) y N(6)
Secuencia propuesta:
N(2) →N(8) Múltiplo (separar de 3 bits en 3 empezando del LSB)
N(2) →N(16) Múltiplo (separar de 4 bits en 4 empezando del LSB)
N(16) →N(10) Multiplicar por base y sumar
N(10) →N(6) Residuos

48. N(2) →N(8) Múltiplo (separar de 3 bits en 3 empezando del LSB)
N(2) →N(16) Múltiplo (separar de 4 bits en 4 empezando del LSB)
N(16) →N(10) Multiplicar por base y sumar
N(10) →N(6) Residuos

49. Ejemplo 2 convertir un número octal N(8)
a N(2), N(10), N(16) y N(5)

50. Ejemplo: convertir un número octal N(8)
a N(2), N(10), N(16)
Secuencia propuesta:
N(8) →N(2) Múltiplo (cada digito corresponde a de 3 bits )
N(2) →N(16) Múltiplo (separar de 4 bits en 4 empezando del LSB)
N(16) →N(10) Multiplicar por base y sumar

51. Ejemplo 2 convertir un número octal N(8)
a N(2), N(10), N(16)
Secuencia propuesta:
N(8) →N(2) Múltiplo (cada digito corresponde a de 3 bits )
N(2) →N(16) Múltiplo (separar de 4 bits en 4 empezando del LSB)
N(16) →N(10) Multiplicar por base y sumar